聚丙烯載流子輸運與能量積累調制直流擊穿威布爾分布特性仿真研究

蔡姝嬈 高梓巍 紀民尊 姚佳池 李鵬新 閔道敏 李盛濤 武慶周

(1. 西安交通大學電力設備電氣絕緣國家重點實驗室 西安 710049； 2. 中國工程物理研究院流體物理研究所 綿陽 621900)

1 引言

隨著我國能源互聯網的建設和能源系統的轉型，薄膜電容器因其微/納秒級的充電速度，優異的耐壓和柔韌性能在柔直輸電工程、脈沖功率技術、電動汽車等領域發揮重要作用。發展高儲能密度、低成本以及安全可靠的薄膜介質材料已成為國內外研究的熱點[1-2]。聚丙烯由于其自身化學結構特點，具備優良的化學穩定性和電氣絕緣性，作為熱塑性樹脂的代表，同時具有良好的可加工性，是薄膜電容器中常用的介質材料[3-4]。然而當介質實際運行在高壓直流電場下時，電荷從電極注入介質內部并受電場力驅動輸運和積累能量，當載流子能量達到閾值時引發擊穿，造成材料永久性破壞。材料的擊穿強度是影響介質薄膜電容器儲能密度的一個關鍵參數，是制約儲能技術發展的重要因素。因此開展對介電材料擊穿強度的研究很有必要。

外施電場作用下載流子定向遷移的過程中，介質中存在的陷阱捕獲、空間電荷積聚、電場畸變、分子鏈位移、能量積累與耗散等過程共同調控直流擊穿性能。TANAKA等[5]提出的界面區多核模型認為電荷受到德拜屏蔽層的庫侖力作用而損失能量會提高介質的擊穿強度；李吉曉等[6-9]認為聚合物的擊穿與空間電荷脫陷時釋放的電機械能有關，空間電荷積聚與電場畸變也會對電介質絕緣性能產生嚴重影響。在以前的工作中，利用仿真研究了電荷輸運參數與宏觀擊穿特性的關 系[10-13]，發現介質中電荷輸運參數是影響擊穿特性的重要因素。

但是當電介質內部載流子輸運與能量積累過程發生波動時，直流擊穿強度分布如何變化，是否符合擊穿威布爾分布，以及描述載流子輸運過程的參數，例如遷移率、注入勢壘、陷阱能級等對威布爾分布的作用規律尚不明確。本文分析了載流子輸運和能量積累造成絕緣電介質擊穿的物理過程，仿真研究了不同電荷輸運隨機變量波動時擊穿強度的威布爾分布特性，得到了電荷輸運參數方差與威布爾分布的關系，闡釋了電荷輸運隨機變量通過調控載流子輸運與能量積累改變擊穿威布爾分布特性的作用機理。

2 電介質直流擊穿過程

考慮受電荷輸運和分子鏈位移調制的電介質直流擊穿過程(CTMD模型)，如圖1所示。圖1a中，x=0和x=d處分別是陰極和陽極(d是材料厚度)，介電材料置于兩電極之間，對介質施加斜率為kramp的斜坡電壓作為模型邊界條件，電場對空間位置滿足積分方程

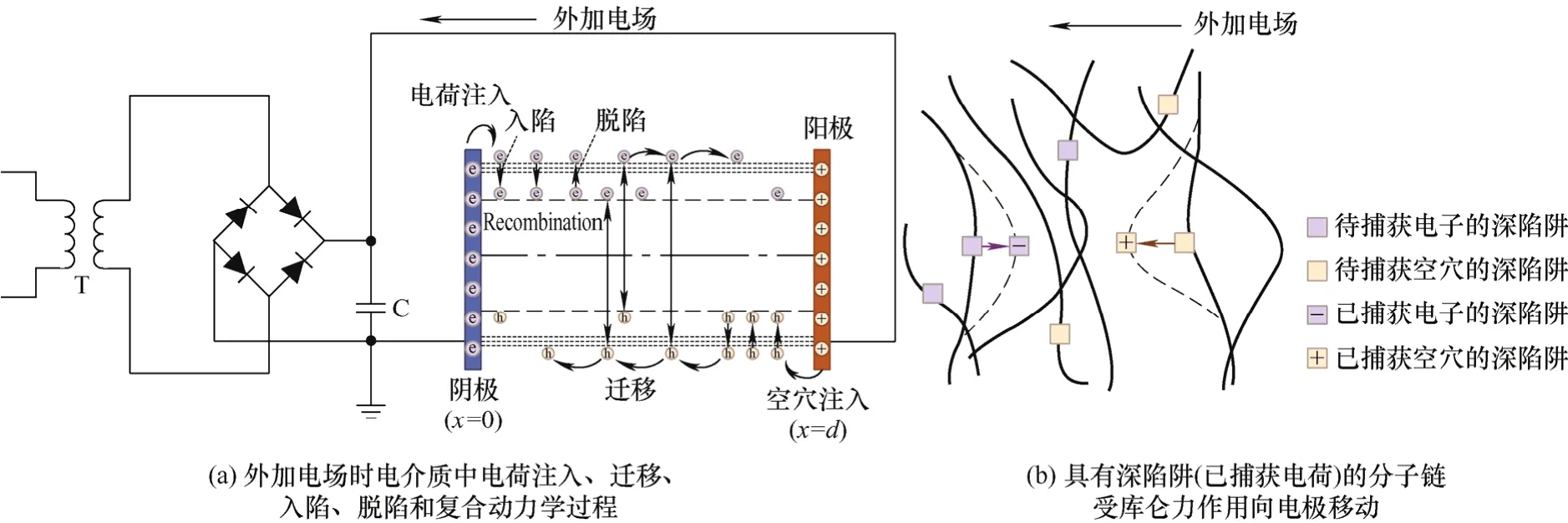
圖1 電荷輸運與分子鏈位移調制擊穿模型示意圖

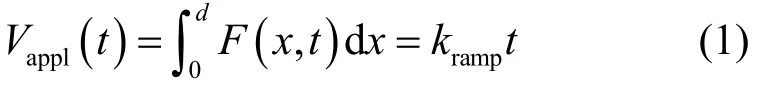
式中，Vappl為外施電壓，V；kramp是升壓速率，V· s?1。

在外加電場作用下，電極通過肖特基熱發射向介質內部注入電荷[14]，場助熱發射電荷對應的注入電流密度與溫度、電場、注入勢壘、試圖逃逸頻率等有關。

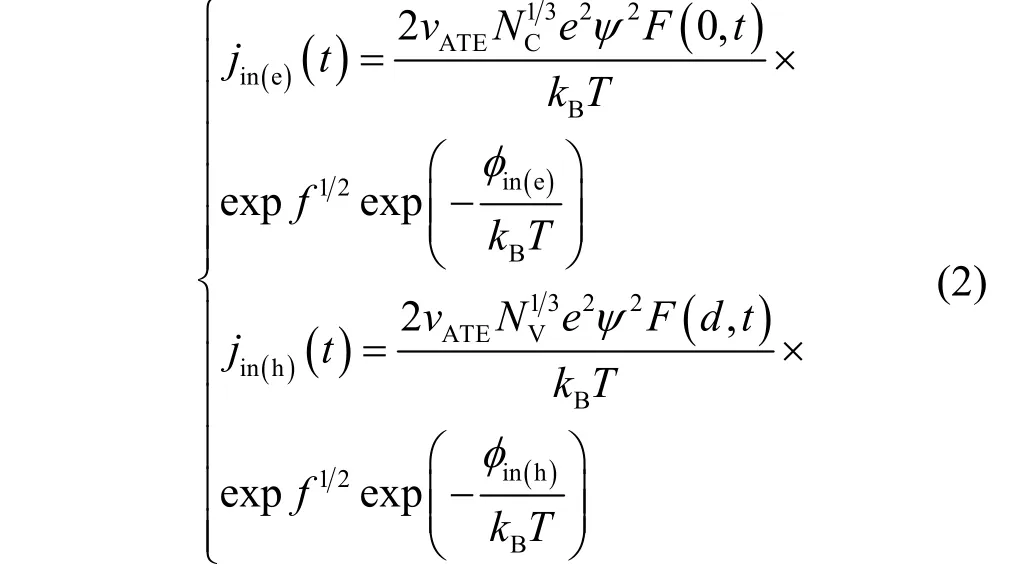
式中，jin(e)(t)和jin(h)(t)分別為陰極和陽極的注入電流密度，A·m?2；vATE為試圖逃逸頻率，s?1；NC和NV分別為導帶和價帶狀態密度；F(0,t)和F(d,t)分別為陰極和陽極處電場；φin(e)和φin(h)分別為介質與陰極和陽極間的注入勢壘，eV；kB為玻爾茲曼常數；f為電場下降系數，由庫侖半徑rc、電場強度F和溫度T決定，表達式為f=eFrc/kBT，庫侖半徑rc公式為rc=e2/4πε0εrkBT，ε0εr是材料介電常數；參數ψ可被表示為ψ(f) =f?1+f?1/2?f?1(1+2f1/2)1/2，ψ與電場強度F相關。

電介質不能完全屏蔽外加電場，注入到介質內部的電荷將受電場力作用定向遷移并積累能量，形成的傳導電流與遷移率、電荷密度和電場有關，用本構方程表達[11,15-16]

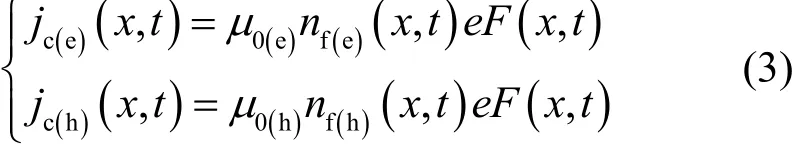
式中，jc(e)和jc(h)分別為電子和空穴傳導電流密度，A·m?2；nf(e)和nf(h)分別為自由電子和自由空穴密度，m?3；μ0(e)和μ0(h)分別為電子和空穴的遷移率，m2·V?1·s?1。

根據能帶理論，物理缺陷(例如構像不規則)會在介質導帶或價帶附近形成局域態能級，即淺陷阱；而化學缺陷(例如極性基團)會在費米能級附近形成局域態能級，即深陷阱[17]。遷移過程中的載流子會受到極性基團陷阱的強庫侖力作用，當庫侖力足夠大時，載流子有概率被陷阱捕獲，載流子能量轉移到原子或分子上，造成能量耗散，有利于提高擊穿強度。當陷阱中電荷能量超過陷阱勢壘時，可通過熱激發過程脫陷，繼續在介質內部遷移；而當陷阱電荷能量不足以躍過陷阱勢壘時，會形成穩定的空間電荷，使電場發生畸變，且介質內最大局部場強隨著空間電荷的積聚而增強。介質中電子與空穴相遇時會發生復合，本模型假設存在三對電荷復合，即自由電子/自由空穴、自由電子/陷阱空穴和陷阱電子/自由空穴，且正負電荷復合會導致電荷湮滅，不產生第三類中性電荷。電荷遵守通量平衡方程組(即電荷守恒方程和泊松方程)[10,18]。

介質中自由電子、自由空穴、陷阱電子和陷阱空穴四種電荷的遷移、入陷、脫陷和復合過程滿足電荷守恒方程[11,15-16]

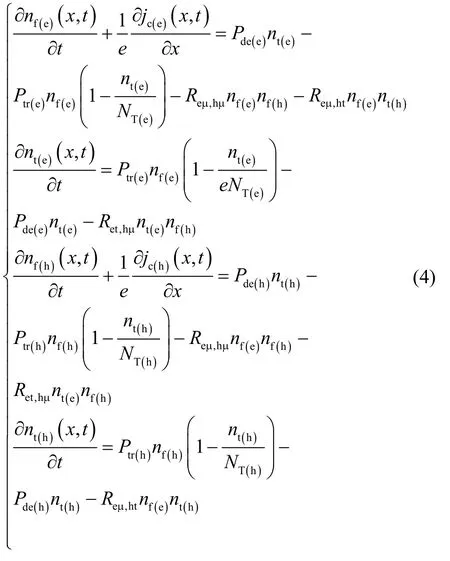
式中，nf(e)、nf(h)、nt(e)和nt(h)分別為自由電荷、自由空穴、陷阱電荷以及陷阱空穴密度，m?3；Ptr為陷阱捕獲概率，Pde為陷阱電荷脫陷概率，Pde=vATEexp(?ET/kBT)；NT為陷阱密度，m?3；Reμ,hμ、Reμ,ht、Ret,hμ為電荷復合系數，m3·C?1·s?1，其中下標e或h表示電子或空穴，下標μ或t代表自由電荷或陷阱電荷。根據 Langevin復合模型[19]和Shockley-Read-Hall模型[20-21]，三種復合系數為

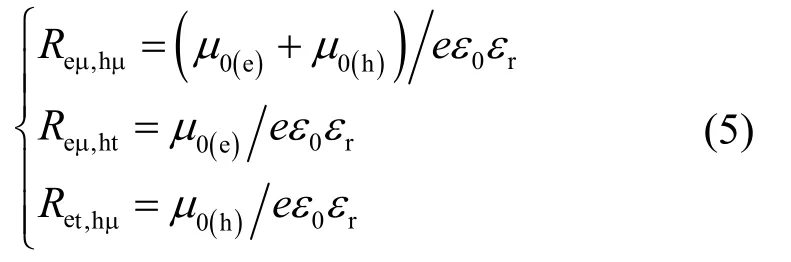
電荷和電場關系滿足泊松方程

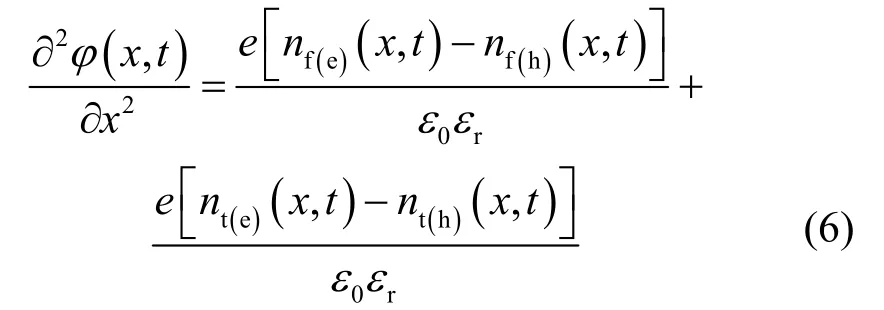
式中，方程邊界條件?(0)=0 V，?(d，t)=Vappl(t)。e為元電荷量，C。

當可動載流子被極性基團陷阱捕獲并停留在陷阱中時，庫侖力持續存在，與極性基團通過共價鍵相接的分子鏈受力發生定向位移導致自由體積擴 張[22-23]。如圖1b所示，分子鏈連接的極性基團陷阱捕獲電子時分子鏈向陽極移動、捕獲空穴時分子鏈向陰極移動。電荷在陷阱中的停留時間決定了分子鏈受庫侖力的持續時間，從而影響分子鏈位移大小，能級更大的陷阱中陷阱電荷保留時間更長，對應分子鏈的受力時間更長。在陷阱電荷所受庫侖力的驅動下，與極性基團連接的分子鏈運動速度方程為

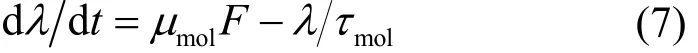
式中，λ為分子鏈位移，m；μmol為分子鏈遷移率，m2·V?1·s?1；τmol為分子鏈弛豫時間常數，s，等于電荷在陷阱中的停留時間，與陷阱能級和溫度等相關，即τmol=τ0exp(ET/kBT)。

介質中的載流子會在庫侖力作用下分子鏈運動導致擴張的自由體積中被電場持續加速、能量積累，載流子能量取決于局部電場和局部自由體積長度，即w=eFλ，當載流子積累的能量超過一定閾值(陷阱能級)時，載流子會持續定向遷移并觸發擊穿，擊穿引發方式有多種可能：載流子遷移在局部形成的大電流和大焦耳熱可能引發局部放電導致擊穿；高能載流子也可能發生劇烈碰撞電離產生大量電子從而引發雪崩擊穿；此外，載流子也有概率碰撞介質分子造成化學鍵斷裂進而發生擊穿。

3 電荷輸運參數的提取

根據以上對電介質直流擊穿過程的分析，發現載流子輸運和能量積累是導致電介質在外施電場作用下發生擊穿的關鍵過程。從載流子輸運和能量積累造成擊穿的過程中可提煉出六個電荷輸運特征參數：試圖逃逸頻率、電荷注入勢壘、載流子遷移率、陷阱能級、陷阱密度和陷阱捕獲概率。

在外施強電場作用下，電極與電介質界面上的電荷通過肖特基熱發射越過注入勢壘到達導帶，為介質提供大量載流子，載流子受到電場力作用定向遷移形成電流。而試圖逃逸頻率降低或注入勢壘提高會使得電極電荷不易越過勢壘注入介質，從而減小了遷移載流子和電流密度，電阻率提高，同時，載流子密度減小也會降低介質體內空間電荷積聚量，使得空間電荷引起的電場畸變減弱，最終表現為擊穿場強的提高。介質中載流子遷移率的降低會減小電流密度進而提高體電阻率，提升擊穿性能。

陷阱能級、陷阱密度或陷阱捕獲概率增大時可增強介質體內陷阱捕獲效應，載流子定向遷移過程受到阻礙，介質內部載流子遷移率和局部電流密度降低，體電阻率升高；同時，電荷被陷阱捕獲后積聚在電極附近形成同極性空間電荷，根據泊松方程，這大大削弱了電極/界面處的等效電場，電荷注入過程受到抑制，介質內空間電荷積聚和電場畸變減弱，擊穿場強提高；此外，陷阱捕獲電荷的過程中載流子能量耗散，電場畸變的減弱也會減慢載流子能量積累過程，有利于擊穿性能的提升。三個因素共同作用使得增大陷阱能級、陷阱密度或陷阱捕獲概率時直流擊穿強度提升。

模型中電荷輸運參數的變化會改變電荷輸運和分子鏈位移與自由體積擴張特性，調控輸載流子輸運與能量積累過程并進而影響擊穿強度。

4 基于CTMD模型的載流子輸運與能量積累調制直流擊穿威布爾分布仿真

4.1 仿真參數與數值方法

高斯分布是建模仿真中的常用模型，可以用來模擬電荷輸運變量的波動行為。將提煉出的六個電荷輸運參數設置成期望值(來源于聚丙烯的TSDC、介電譜、電位衰減等試驗結果)如表1所示，服從高斯分布的50維向量作為隨機變量，輸運隨機變量方差非零時可仿真載流子輸運以及分子鏈位移和自由體積擴張過程的波動，進而調控載流子能量積累與耗散過程。基于CTMD模型通過Matlab采取高階精度間斷伽遼金法和有限元法數值求解自洽方程組式(1)～(7)，可計算得到一組(50個)具有分散性的擊穿強度。

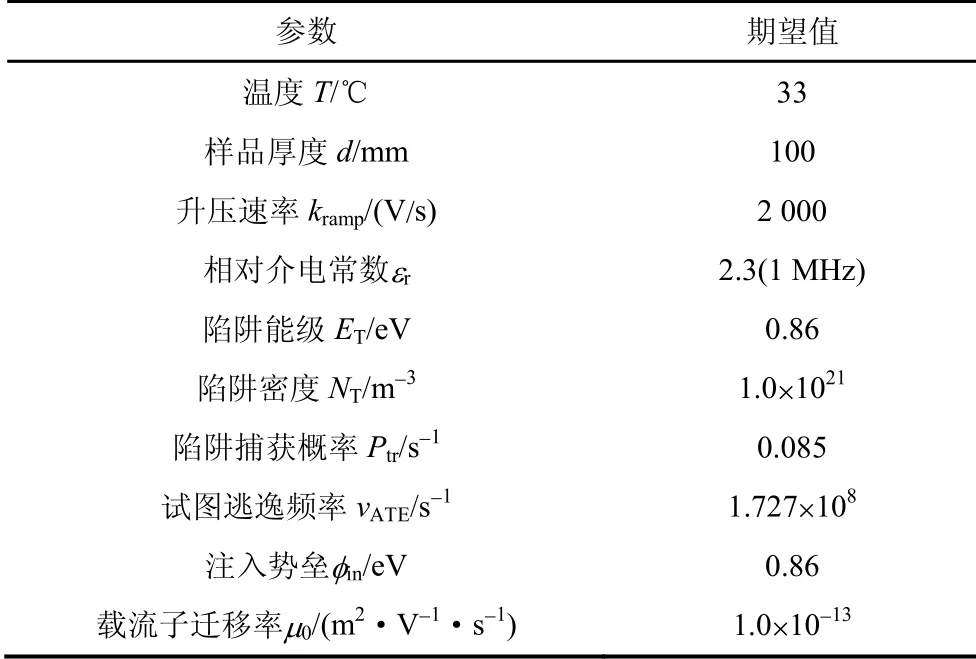
表1 CTMD模型仿真中的參數設置

4.2 擊穿過程的仿真結果與討論

采用CTMD模型仿真載流子輸運與能量積累過程，當各隨機變量方差為0時得到從加壓到擊穿的過程中，介質電壓在斜坡電壓源作用下以設定斜率升高時，介質內部空間電荷、電場強度、分子鏈位移、載流子能量分布隨加壓時間的演變特性，如圖2所示。

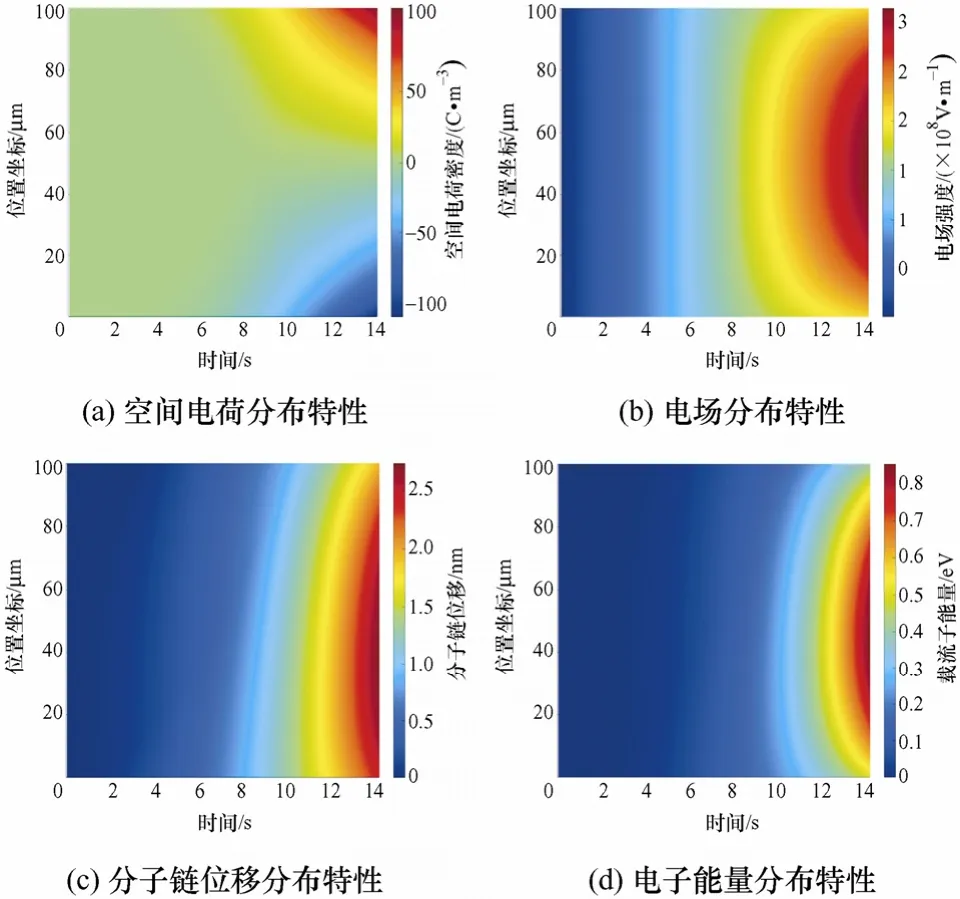
圖2 介質內部空間電荷、電場、分子鏈位移和載流子能量分布隨升壓時間變化的數值結果

在前6 s時間內，外加場強未達到電荷注入的臨界電場，電荷注入不明顯，而當6 s后，外加電場達到一定值，電荷注入量明顯增多，注入電荷被陷阱捕獲形成同極性空間電荷積聚在電極附近，載流子難以向介質內部遷移，如圖2a所示，隨著加壓時間增加，電極附近空間電荷積聚量持續增大，電介質在6 s、10 s和14 s時陰極附近電荷空間電荷密度分別為?5.32 C·m?3、?37.49 C·m?3和?107.61 C·m?3，隨著空間電荷分布逐漸向介質體內發展，在介質中部正、負電荷相遇并相互中和，此處空間電荷積聚較少，因此從電極附近向介質內部空間電荷積聚逐漸減少，14 s時陰極、介質中間和陽極處空間電荷密度分別為?107.61 C·m?3、?0.04 C·m?3和107.04 C·m?3。圖2b為電場分布圖，前6 s內，介質內部各處電場分布均勻，這是因為初始階段無明顯的空間電荷積聚使電場畸變[24]，隨著時間或外施電壓增大，電場持續增大，6 s、10 s和14 s時介質體內最大電場分別為120.02 kV·mm?1、212.18 kV·mm?1和310.58 kV·mm?1。當外施電壓較大時，發現電場分布明顯畸變，從電極/介質邊界到介質內部場強增大，這與空間電荷的積聚密切相關。根據泊松方程，電極附近的同極性空間電荷會建立反向電場(與外施電場反向)從而減小該處等效電場[7]，相反介質內部電場在疊加空間電荷建立的同向電場作用后持續增強，14 s時陰極、介質中間和陽極處的電場強度分別為208.16 kV·mm?1、310.58 kV·mm?1和209.20 kV·mm?1。圖2c為分子鏈位移分布圖，當介質中陷阱捕獲電荷時，與極性基團相連接的分子鏈因捕獲電荷受到電場力作用而發生定向位移，根據分子鏈動力學公式(7)，當只保留右邊第一項，不考慮第二項分子鏈弛豫時間常數對分子鏈運動影響時，式(7)簡化為dλ/dt=μmolF，若忽略空間電荷積聚導致的電場畸變效應，即F=krampt，并考慮初始條件λ(t=0)=0，可得λ=(krampμmol/2d)t2，分子鏈位移與時間的平方成正比，6 s、10 s和14 s時局部最大分子鏈位移分別為0.49 nm、1.33 nm和2.71 nm。若考慮電場畸變，從電極/介質邊界到介質內部分子鏈位移逐漸增大，與電場分布規律一致，14 s時陰極、介質中間和陽極處的分子鏈位移分別為2.39 nm、2.68 nm和1.92 nm。圖2d為載流子能量分布圖，分子鏈的定向運動會擴張局部自由體積，假設自由體積長度等于分子鏈位移，載流子在擴張的自由體積中被電場持續加速、能量增大，其能量與局部電場和分子鏈位移有關，即w=eFλ，6 s、10 s和14 s時介質局部最大載流子能量積累分別為0.06 eV、0.27 eV和0.83 eV。且載流子能量分布不均，局部場強較大處載流子積聚能量更多，14 s時陰極、介質中間和陽極處的載流子能量積累分別為0.50 eV、0.83 eV和0.40 eV。12～14.1 s時間內(臨近擊穿)，空間電荷積聚引發嚴重的電場畸變，介質內局部電場增強、局部自由體積擴張劇烈，導致此處載流子積累能量急劇增大，直至在14.1 s時載流子能量積累超過陷阱能級，載流子將在介質內部自由遷移不被陷阱捕獲，局部電流密度和局部溫度激增，同時運動過程中的載流子也可能碰撞高分子材料晶格而觸發劇烈的碰撞電離或使得高分子化學鍵斷裂，導致擊穿。

4.3 威布爾分布的仿真結果與討論

單獨調節每個電荷輸運隨機變量的方差，得到一組擊穿強度計算結果并用威布爾分布擬合。威布爾分布是一種基于弱點理論廣泛應用于壽命診斷和可靠性分析的方法，雙參數威布爾分布被廣泛用于介質電擊穿性能分析，其表達式為

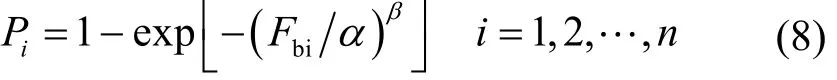
式中，α為特征擊穿強度(累計概率為63.2%)，kV·mm?1；β為形狀分布參數，表征擊穿場強分散程度，β與分散程度成負相關。將一系列擊穿電壓從小到大排列，用i=1, 2 , …,n編號，Ross函數Pi=(i?0.44)/(n+0.25)表示第i個擊穿電壓對應概率；n為樣品個數。

圖3為與陷阱特性相關的三個電荷輸運隨機變量方差不同時得到的擊穿強度計算結果威布爾分布圖，σ為高斯分布標準差，圖3a中當陷阱能級的σ分別為0.000 1、0.001、0.003、0.005和0.01時，威布爾形狀分布參數分別為214.54、117.22、30.82、17.34和7.74。圖3b中陷阱密度的σ從0.000 1遞增到0.1，發現得到的擊穿強度始終為定值，不符合威布爾分布。圖3c中當陷阱捕獲概率的σ分別為0.001、0.01、0.05、0.1、0.15、0.2、0.24、0.26時，形狀分布參數分別為3 987.51、313.72、96.66、37.54、29.09、22.46、16.33、12.55。結果表明，基于本模型，陷阱能級或陷阱捕獲概率為符合高斯分布的隨機變量時，得到的擊穿強度服從威布爾分布，且改變隨機變量方差可調制威布爾分布特性，具體地，方差增大時擊穿數據分散性增大，從而形狀分布參數減小。而陷阱密度為符合高斯分布的隨機變量時，得到的擊穿強度一定，這是因為本模型中假設電荷捕獲概率為定值0.085 s?1，肖特基電荷捕獲模型認為捕獲概率表達式為：Ptr=vScNT，其中v為電子運動速度、Sc為陷阱捕獲面積，NT為陷阱密度[20,25]，陷阱密度的波動可改變捕獲概率進而影響擊穿強度，但本文模型未考慮陷阱密度對捕獲概率的影響，導致擊穿強度計算結果不具有分散性。

圖3 陷阱特性隨機變量對應的威布爾分布圖

圖4 為試圖逃逸頻率、注入勢壘和載流子遷移率三個電荷輸運隨機變量方差不同時得到的威布爾分布圖，圖4a中當試圖逃逸頻率的σ分別為0.001、0.01、0.05、0.1、0.15、0.17、0.2、0.26時，威布爾形狀分布參數分別為2 896.81、391.90、68.85、28.45、19.85、17.99、15.36、13.89，圖4b中當注入勢壘的σ分別為0.001、0.01、0.05、0.1、0.15、0.2、0.24、0.26時，形狀分布參數分別為1 698.01、193.75、39.77、23.50、18.60、17.09、16.95、13.96，圖4c中當載流子遷移率的σ分別為0.001、0.01、0.05、0.1、0.15、0.17、0.2、0.26時，形狀分布參數分別為3 779.03、372.30、50.85、42.07、21.05、17.84、14.21、9.22。結果表明，基于本模型，試圖逃逸頻率、注入勢壘或載流子遷移率為符合高斯分布的隨機變量時，得到的擊穿強度服從威布爾分布，且形狀分布參數隨輸運隨機變量方差的增大而減小，改變隨機變量方差可調制威布爾分布特性。

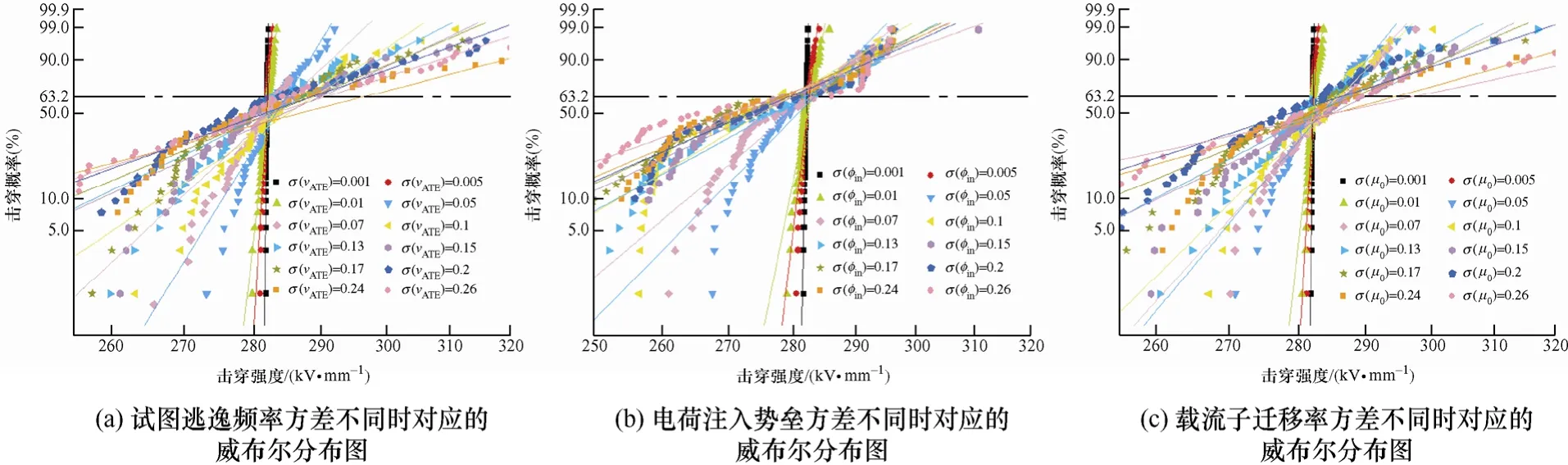
圖4 其他電荷輸運隨機變量對應的威布爾分布圖

通過計算機控制電壓擊穿測試儀(HJC-100kV，華陽儀器有限公司，揚州，中國)，使用直徑25 mm的球球銅電極進行直流擊穿試驗(33 ℃)，得到聚丙烯直流擊穿威布爾分布的特征擊穿強度為281.5 kV·mm?1，形狀分布參數為17.0。根據圖3和圖4，本模型中陷阱能級、陷阱捕獲概率、試圖逃逸頻率、注入勢壘和遷移率五個電荷輸運參數會引起威布爾分布變化，對比仿真結果與試驗結果，建立威布爾形狀分布參數與以上五個輸運隨機變量方差的關系，如圖5所示。顯然變化曲線呈現下降趨勢，形狀分布參數隨著方差的增加而減小。這是因為輸運隨機變量方差的增大會增強載流子輸運和能量積累過程的波動，提高擊穿數據分散性，從而減小形狀分布參數。

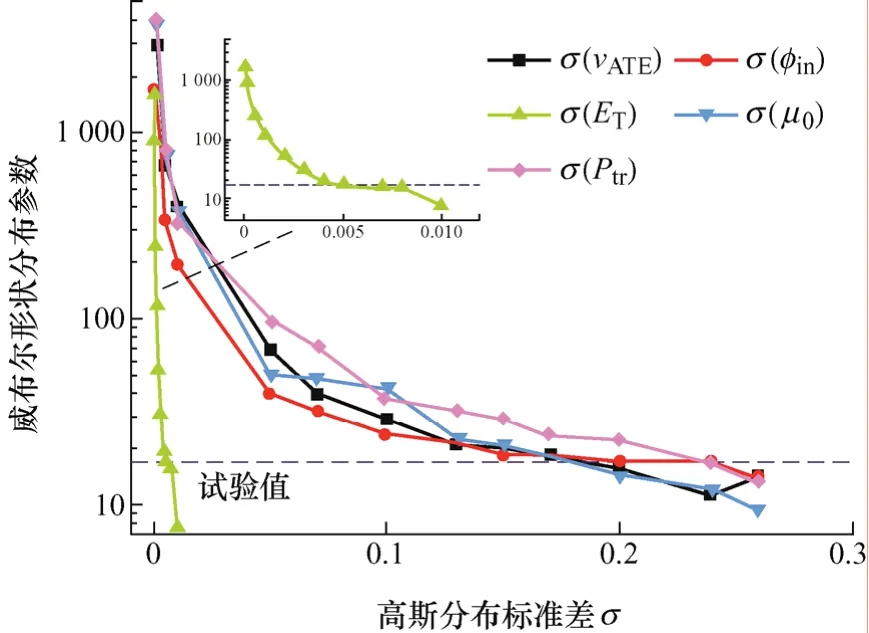
圖5 威布爾形狀分布參數與輸運隨機變量方差關系圖

對比各曲線變化趨勢，發現形狀分布參數隨陷阱能級方差增大而減小的速率最快，說明威布爾分布對陷阱能級方差變化的敏感度最強，強于其他電荷輸運參數。試圖逃逸頻率、遷移率、注入勢壘和捕獲概率四個參數的曲線下降趨勢類似，在σ較小(0<σ<0.05)時，形狀分布參數隨著σ的增大而大幅下降，當σ增大到0.05時下降趨于平緩，幾何效應參數逐漸趨向于試驗值，當σ>0.26時，擊穿數據分散性過大，在實際應用中不具有參考價值。

當威布爾形狀分布參數與試驗結果一致時，陷阱能級、試圖逃逸頻率、遷移率、注入勢壘、捕獲概率對應的?σ依次增大，分別為0.005、0.17、0.17、0.24、0.24。說明基于此模型，威布爾分布對陷阱能級的依賴性最強，對試圖逃逸頻率和遷移率的依賴性較弱，對注入勢壘和陷阱捕獲概率的依賴性最弱。

陷阱能級增大會增加電荷在陷阱中的弛豫時間，即τmol=τ0exp(ET/kBT)，從而增強陷阱捕獲效應，擊穿強度提高。根據式(2)可得，試圖逃逸頻率或注入勢壘都與電極注入電流有關，會影響擊穿強度，但試圖逃逸頻率是注入電流密度的線性系數項，而注入勢壘與1/kBT相乘后是注入電流密度的負指數項，這可能是二者對威布爾分布影響相異的原因。捕獲概率為式(4)中Ptr，發現其對電荷脫陷入陷的影響受到系數1?qt/qeNT的作用，陷阱密度NT越大時，1?qt/qeNT越大，捕獲概率波動對介質電荷輸運和能量積累過程的影響越明顯，對威布爾分布的調制作用越強。在本模型NT為1.0×1021m?3的條件下，捕獲概率對威布爾分布的影響比較弱。遷移率在電荷遷移和復合過程中作為前置系數對威布爾分布產生影響，見式(3)和式(5)。

建立威布爾特征擊穿強度與五個輸運隨機變量方差的關系，如圖6所示。結果表明，隨著方差的增大，特征擊穿強度由于仿真數據的隨機性而略有波動，但其最小值277.6 kV·mm?1、最大值297.2 kV·mm?1始終穩定在試驗值281.5 kV·mm?1附近，誤差小于5.6%。說明利用本模型進行直流威布爾仿真可以有效模擬擊穿過程，得到較準確的特征擊穿強度。

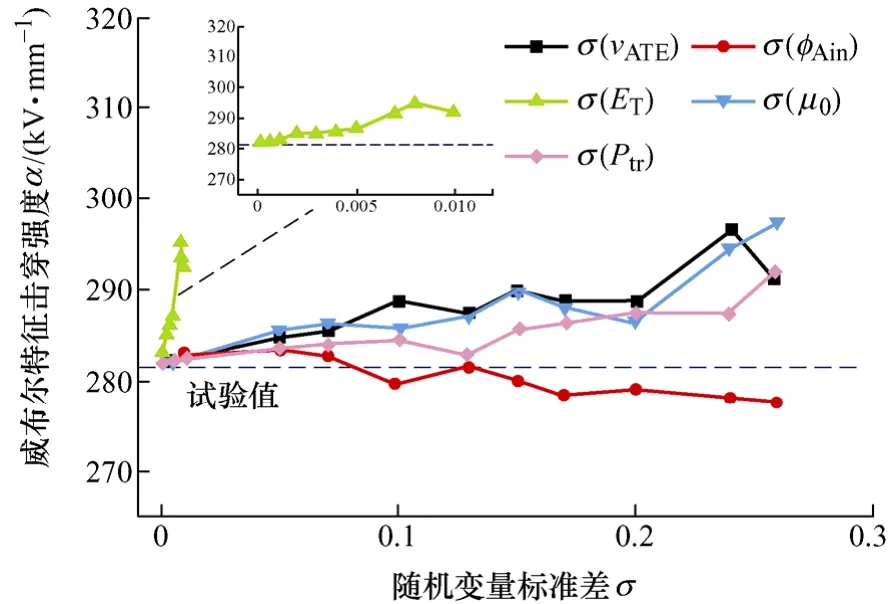
圖6 威布爾特征擊穿強度與輸運隨機變量方差關系圖

圖7為形狀分布參數仿真值與試驗值基本一致時，各個電荷輸運隨機變量歸一化后的可能分布范圍，分布范圍寬度可反映此電荷輸運參數對威布爾分布的影響程度，寬度越小，影響越強。對比發現陷阱能級的分布范圍最小為0.02，說明歸一化的陷阱能級產生0.02的微小波動，即可引發介質內電荷輸運和能量積累特性劇烈波動，使得擊穿強度的形狀分布參數下降至17.34，對威布爾分布調制效果明顯。由圖7可知，本模型中，陷阱能級是影響威布爾分布的主導參數，其他四個輸運參數對威布爾分布的影響程度相差不大，其中試圖逃逸頻率和遷移率的影響程度略強于注入勢壘和捕獲概率。

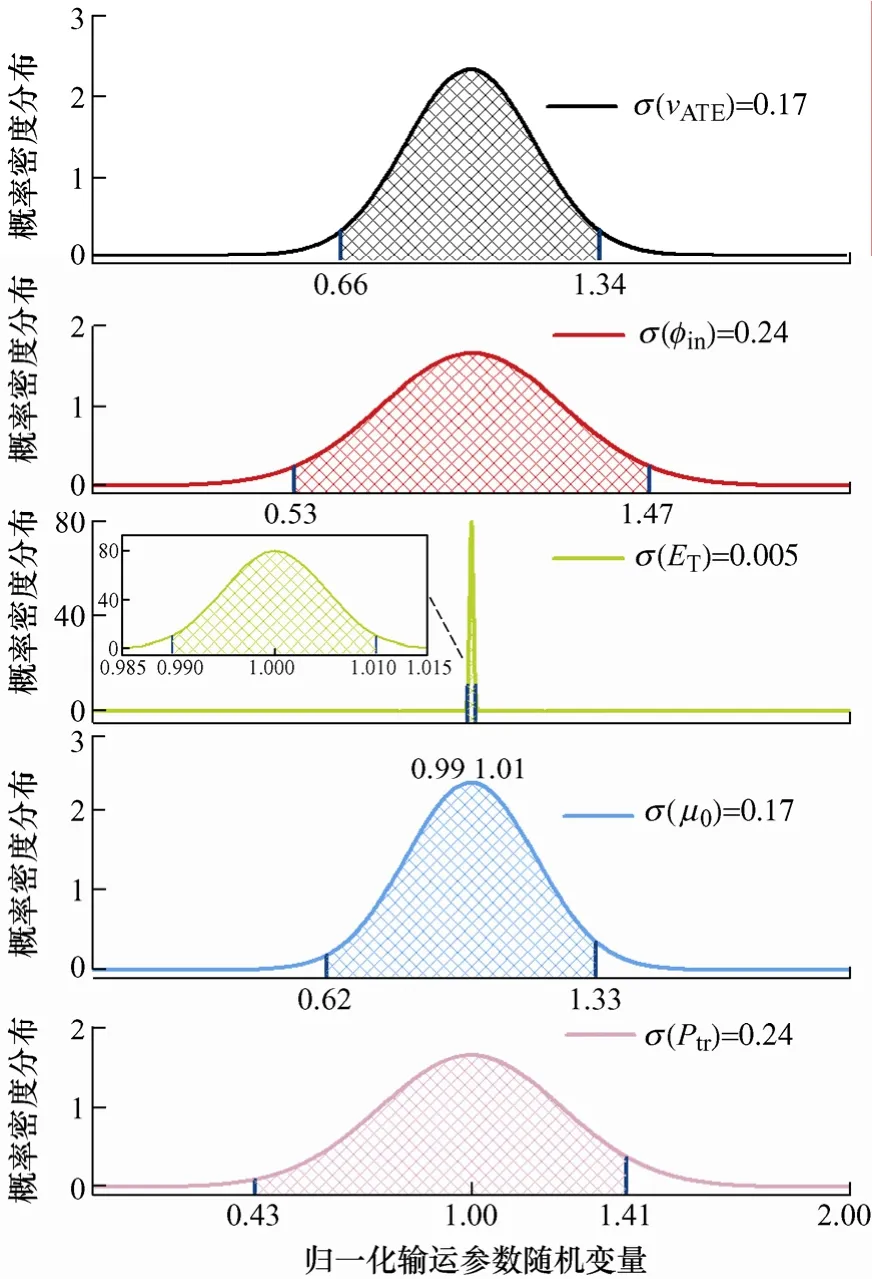
圖7 形狀分布參數與試驗值相符時輸運參數隨機 變量分布范圍

根據圖5結論，威布爾分布對陷阱能級依賴性最強，且陷阱能級方差為2.5×10?5時擊穿強度計算結果的形狀分布參數與試驗結果一致。圖8為陷阱能級方差為2.5×10?5時，聚丙烯直流擊穿試驗和計算結果的威布爾分布圖，發現計算與試驗結果非常吻合，得到威布爾分布參數如表2所示，α計算值與試驗值的誤差小于2.0%；β計算值與試驗值的誤差小于1.8%。表明當陷阱能級可調控威布爾分布特性，其方差為2.5×10?5時可本模型很好地模擬聚丙烯直流擊穿試驗結果的威布爾分布。

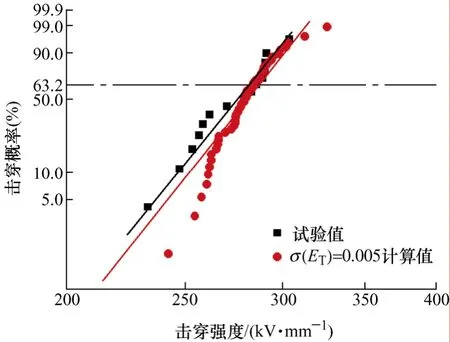
圖8 威布爾分布的計算結果與試驗結果對比

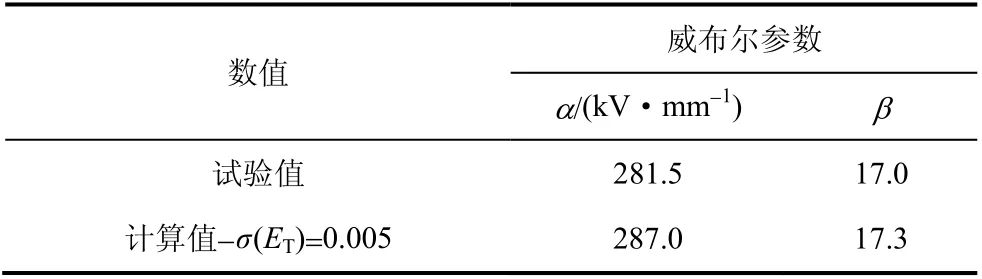
表2 威布爾參數的計算值與試驗值

5 結論

本文研究了電介質體內電荷輸運隨機變量通過調控載流子輸運與能量積累改變擊穿威布爾分布特性的作用機理，得到的主要結論如下。

(1) 闡釋了電介質直流擊穿機理，外施強電場作用下，電極/絕緣電介質界面注入的電荷在電場力驅動下輸運并積累能量，形成泄漏電流，積聚空間電荷、畸變電場，最終導致絕緣電介質發生擊穿。載流子輸運與能量積累為造成電介質擊穿的關鍵物理過程，從中提取出六個特征參數：電荷注入勢壘、試圖逃逸頻率、載流子遷移率、陷阱能級、陷阱密度和陷阱捕獲概率。

(2) 將六個電荷輸運參數設置為符合高斯分布的隨機變量時，可基于CTMD模型仿真載流子輸運與能量積累過程中的波動，當電荷注入勢壘、試圖逃逸頻率、載流子遷移率、陷阱能級和陷阱捕獲概率方差非零時的擊穿強度計算結果服從威布爾分布，陷阱密度在方差非零時得到的擊穿強度計算結果為定值，不具有隨機性，因為本模型未考慮陷阱密度變化對捕獲概率的影響。建立了威布爾特征擊穿強度與形狀分布參數隨不同電荷輸運隨機變量方差的變化關系，隨著方差的增大，特征擊穿強度基本穩定在試驗值附近，形狀分布參數由于擊穿數據分散性增大而下降。

(3) 對比了各輸運參數方差與威布爾分布的關系。陷阱能級、試圖逃逸頻率、載流子遷移率、注入勢壘和陷阱捕獲概率的方差分別為2.50×10?5、2.89×10?2、2.89×10?2、5.76×10?2、5.76×10?2時得到的威布爾形狀分布參數與試驗結果一致。說明威布爾分布對陷阱能級的依賴性較強，對試圖逃逸頻率和遷移率的依賴性較弱，對注入勢壘和陷阱捕獲概率的依賴性最弱。