基于Adaboost 模型的風速預測

楊君琪 劉海忠

(蘭州交通大學,甘肅 蘭州 730000)

目前主流方法依然是數值天氣預報法和時間序列預測,諸如利用經驗小波和高斯回歸的方法綜合預測每小時的風速[2]。在對風速短期預測過程中,統(tǒng)計方法也用來作為一種預測方法,Miranda M S 提出了基本的貝葉斯方法來建立風向預報1 h的自回歸模型[3]。從傳統(tǒng)時間序列分析角度,Lahouar A 和Slama J 提出利用ARMA 模型用于根據時間序列中的過去數據知識進行預測,得到了和好的預測效果[4]。時間序列對于波動較大時預測并不明顯,但是,由于線性特性,ARMA 模型的預測在給定的工作條件下是有效的[5]。而機器學習方法,例如人工神經網絡,利用非線性函數的無限逼近來達到預測目的,很好地抓住了風速非線性的特性,從而擁有較為可觀的預測精度。相比較ARMA 模型,ANN 模型所具有的非線性激活函數,使得在風速波動較大時更能體現出ANN 的優(yōu)勢[6]。諸如Amjady, N 在對風能進行短期預測時引入了嶺函數Ridgelet 神經網絡(RNN)[7]。Sideratos 提出一種新的預測方法,其在預測過程中綜合利用了模糊邏輯與神經網絡,整個預測的魯棒性有顯著的提升[8]。本文嘗試提出一種集成學習模型結合機器學習模型的方法來預測風速,并且與常見的神經網絡模型進行精度比較,在預測精度評價指標方面上,本文選擇均方根誤差(RMSE)作為評價指標,并在最后比較了預測模型的誤差平方的整體表現,得到了較好預測結果。

圖1 原始風速序列樣例

圖2 單一模型預測比較

1 數據說明

本文采用來自美國國家海洋大氣管理局(NOAA)2019 年9月22 日-9 月27 日某地風電設備實測數據進行研究。以2019年9 月22 日數據為例,原始風速數據在采樣過程中以2min 為間隔,當日共采集720 個采樣點,以此建立原始風速序列如圖1所示。

2 BP 神經網絡與RBF 神經網絡預測結果

在本文中,利用BP 單一模型進行預測的特征輸入為1,隱含層節(jié)點個數按照經驗設置為2,輸入層節(jié)點個數為1。即BP神經網絡結構為1-2-1,訓練迭代次數為1000 次,學習率為0.01 最大誤差為0.00001。RBF 神經網絡的核函數選擇高斯徑向基函數。首先選擇訓練數據,本文選擇某地22-26 號的風速數據作為訓練數據,預測27 日的風速整體大小情況,訓練方法是,將前一時刻的風速數據作為神經網絡的輸入,將當前時刻的風速數據作為輸出。得到預測軌跡結果如圖2。

預測精度評價指標：

本文采取均方根誤差作為評判預測精度的評價指標,其計算公式為：

其中N 為風速序列預測值的個數；yt為風速在t 時刻的真實值；y^t為相應t 時刻風速的預測值。

單一預測模型預測過程簡單,但是存在魯棒性較差的情況,一次預測結果在某種程度上并不能說明模型預測的穩(wěn)健性良好,其預測結果或多或少是帶有一定的不確定性存在。為了增加模型的穩(wěn)健性,我們嘗試采用Adaboost 方法來彌補這一不足,由于Adaboost 方法對樣本每一次訓練抽取時的權重不一,這使得最后預測結果更加具有泛化能力,樣本能夠得到充分利用。

3 Adaboost 模型及預測結果

3.1 Adaboost 模型

Adaboost 是集成學習中的一個重要方法,Adaboost 是一種迭代算法,其核心思想是針對同一個訓練集訓練不同的分類器(弱分類器),然后把這些弱分類器集合起來,構成一個更強的最終回歸器(強回歸器)。

圖3 Adaboos 預測方法流程

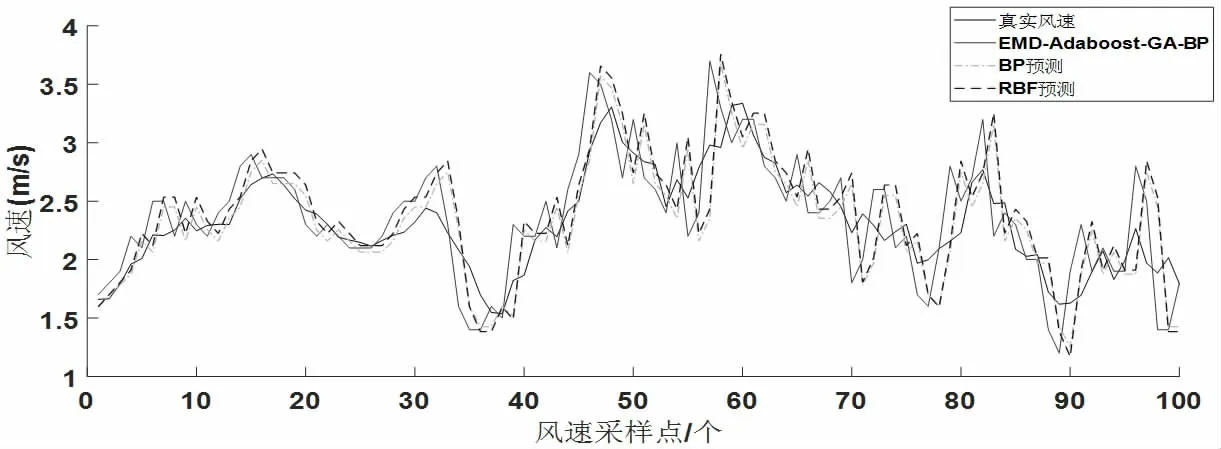
圖4 各預測模型比較

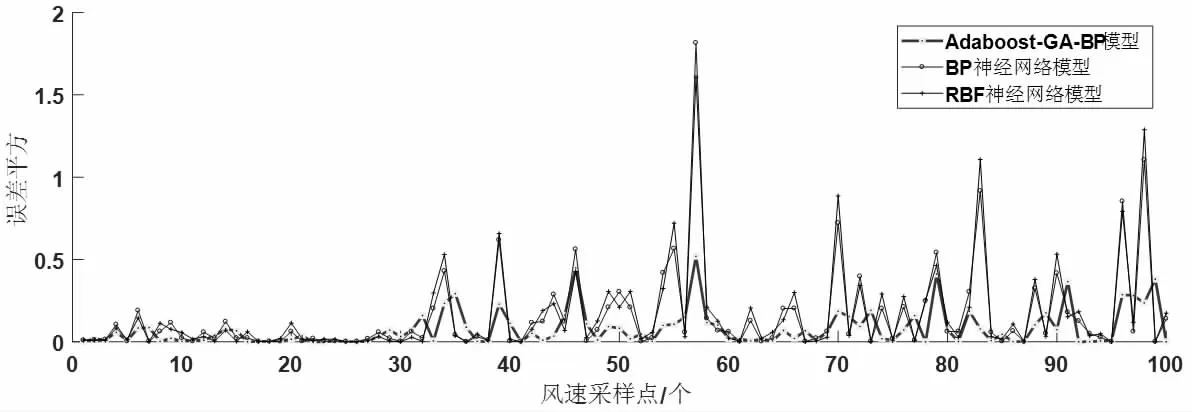
圖5 各預測模型預測整體誤差比較

Adaboost 算法本身是通過改變數據分布來實現的,它根據每次訓練集中每個樣本的分類是否正確,以及上次的總體分類的準確率,來確定每個樣本的權值。將修改過權值的新數據送給下層回歸器進行訓練,最后將每次得到的回歸器融合起來,作為最后的決策回歸器。本文提出的預測方法的整個預測流程為圖3。

其首先對原始數據進行歸一化處理,繼而開始將歸一化后的是數據進行劃分訓練數據與測試數據,通過構造神經網絡進行一級預測,在預測中嵌入Adaboost 框架,本文中所選擇的Adaboost 框架確定迭代次數為10 次,及K=11。由于基回歸器采用BP 神經網絡,而BP 神經網絡有陷入局部最優(yōu)解的缺陷,這里我們采用遺傳算法進行優(yōu)化,使得預測結果更加穩(wěn)定。

3.2 Adaboost 模型預測結果

在這里我們不僅比較本文提出的模型與BP 神經網絡和RBF 神經網絡的精度,進一步,我們通過對每一時刻每個預測值與真實值的誤差平方作比較(圖4),并畫出誤差平方圖來證實本文提出的模型的優(yōu)勢(圖5),與此同時,在預測精度為RMSE的情況下比較常見的神經網絡在預測時的結果(表1)。

表1 各模型預測精度最終比較結果

4 結果與討論

風速預測對風電場風能收集具有重要意義,風速的提前捕捉能有效增強風電采集設備的穩(wěn)定性,使風電場各觀測設備提前做好應對策略；本文采用集成學習Adaboost 與機器學習ANN相結合的方式對風速數據進行預測,結果表明其預測的精度較單一預測模型有較好的優(yōu)勢；采用Adaboost 方法,有效彌補了單一預測模型穩(wěn)健較差的缺陷,圖5 對集成之后的預測模型進行預測后與單一模型進行誤差平方的整體比較,顯示出在加入Adaboost 模型后整體的預測穩(wěn)健性有了明顯的提升,其各預測點預測結果的誤差平方基本小于單一模型。同時對基回歸器BP 神經網絡進行參數優(yōu)化,采用傳統(tǒng)遺傳算法,進而使BP 神經網絡跳出局部最優(yōu)解情況,提高了預測精度,通過個預測模型的比較(表1),Adaboost-GA-BP 模型的預測精度由于本文中涉及到的各預測模型。由于機器學習模型在不斷產生新的方法,基于Adaboost 模型的風速預測有待進一步的進行優(yōu)化。而本文并未將涉及與風速相關的其他因素例如濕度、溫度、風向等作為同等輸入特征,因此對于其他特征對風速變化的研究并沒有涉及,將作為后期重點研究對象進行展開。