尾翼EFP成型及氣動的數值模擬

丁 豐，趙太勇，楊寶良，付建平，印立魁，陳智剛，王維占

(1 中北大學機電工程學院，太原 030051；2 中北大學地下目標毀傷技術國防重點學科實驗室，太原 030051；3 西安現代控制技術研究所，西安 710065)

0 引言

EFP因其不受炸高限制，能從100～150 m距離處對目標發起攻擊，近年來國內外學者進行了大量理論與試驗研究。從EFP形成機理出發，Li等[1]研究了環形多點起爆對EFP成形特性的影響。Berner,Rondot 等[2-3]對EFP的飛行穩定性和終點彈道進行了一系列的分析，總結出具有良好飛行穩定性的EFP形狀，如雙裙體，尖拱形頭部等；Liu等[4]研究了EFP的氣動特性，提出尾翼結構能夠有效改善EFP的飛行穩定性，并減少EFP的飛行阻力；任芮池等[5]應用工程計算方法系統研究準球形、桿式、單尾裙EFP的氣動參數隨特征尺寸的變化規律，并分析了EFP的升阻力系數隨攻角的變化情況；門建兵等[6]采用AUTODUN-3D軟件對異形殼體和多點起爆EFP進行研究，得到不同形狀尾翼的侵徹體；張孝忠等[7]研究了刻槽藥型罩對EFP成形的影響，得到了不同長徑比的尾翼EFP;龍源等[8]研究了多點起爆對雙層藥型罩成形及侵徹的影響，結果表明當起爆點數在4～8時，雙層藥型罩EFP戰斗部能夠形成具有較好空氣動力學特性的侵徹體；劉健峰等[9]研究了偏心起爆對EFP成形及氣動的影響；時黨勇，唐平江等[10-11]研究了殼體對EFP形成尾翼的影響；沈慧銘，陸鳴，李成兵等[12-14]研究了多點起爆對EFP成形的影響。

目前公開的文獻主要研究殼體材料和形狀，藥形罩材料和形狀，裝藥等對EFP成形的影響。但對尾翼EFP的成型及氣動的綜合評判還鮮有報道。文中利用LS-DYNA獲得尾翼EFP,通過UG逆向工程得到EFP的幾何模型，然后利用FLUENT軟件對EFP進行氣動分析，得到最利于發揮EFP終點效應的起爆半徑。

1 尾翼EFP成型數值模擬

1.1 戰斗部結構設計

殼體外表面為正六邊形，外接圓直徑120 mm，為減少影響因素，省略頂部殼體[15]，裝藥高度Hw=100 mm，采用六點起爆的方式，爆點在六邊形的對角線上，裝藥直徑為D=100 mm，藥形罩的外半徑為151 mm，內半徑為160 mm，戰斗部結構示意圖如圖1所示。

圖1 戰斗部結構示意圖

1.2 尾翼EFP成形數值模擬

為得到清晰的尾翼形狀，采用Lagrange算法。利用True Grid軟件建立三維有限元模型，網格類型均使用Solid164八節點六面體單元。在炸藥、殼體、藥型罩相互之間均使用自動面面接觸。殼體材料為45#鋼，藥型罩為紫銅，為了模擬能承受大應變、高應變率的材料，其本構關系模型均采用Johnson-Cook模型。主裝藥選用8701，選用HIGH_EXPLOSIVE_BURN材料模型和JWL狀態方程來描述,其主要材料參數見參考文獻[15]。圖2為戰斗部計算的初始網格。

圖2 聚能裝藥戰斗部計算模型

數值模擬總共計算了中心點起爆及不同起爆半徑下EFP的成型，圖3為各工況下的成型情況。

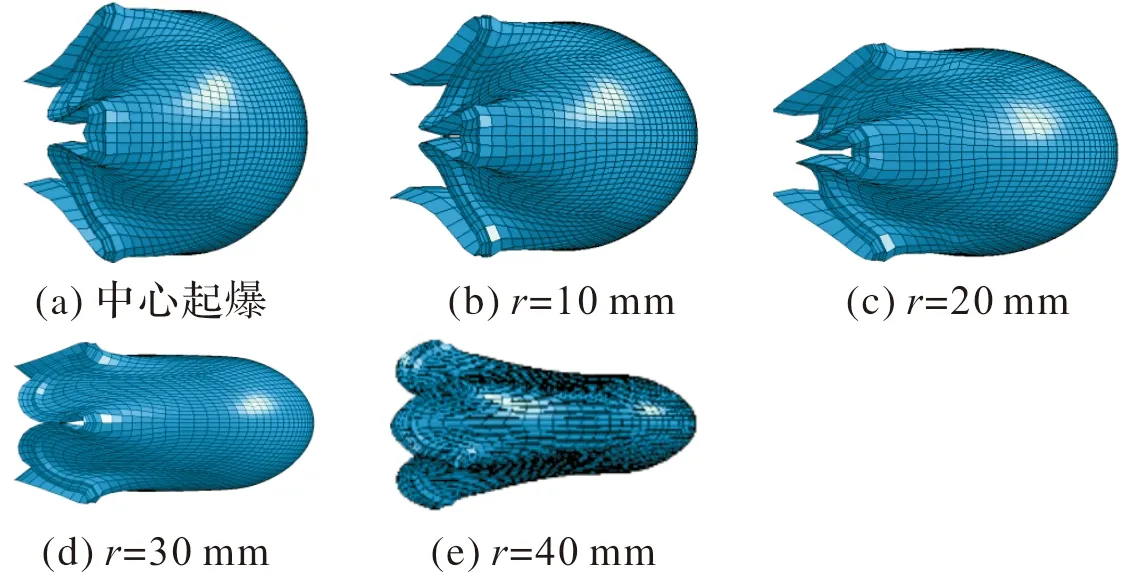
圖3 各工況EFP成型

2 尾翼EFP氣動特性計算模型

2.1 氣動特性數值計算模型

由于LS-DYNA并不能直接對爆炸成型彈丸進行氣動分析。因此將計算得到的爆炸成型彈丸在LS-PREPOST中導出STL格式，將模型導入UG中進行逆向建模，得到EFP的幾何模型。尾翼EFP的幾何外形復雜，曲率變化大，因此采用Mesh劃分為四面體網格，由于幾種工況下的EFP模型處理方法一致，圖4僅給出起爆半徑r為40 mm時EFP的幾何模型及有限元模型。

圖4 EFP模型

將模型導入Fluent進行邊界條件設置。研究物體的運動速度小于0.3Ma時的氣動特性可忽略空氣的可壓縮性。文中研究EFP的運動速度在4Ma～6Ma之間，因此需考慮空氣的可壓縮性。使用雙精度計算，選用Density-based求解器，將空氣選為理想氣體。為適應空氣的高馬赫數流動，將粘度模型選為Sutherland。湍流模型選用k-omega雙方程模型，考慮空氣的能量變化，打開能量方程。將流體入口設置為壓力遠場。

2.2 EFP空氣動力

EFP在空氣中飛行時，受到空氣動力的作用，空氣動力的大小取決于EFP的外形、飛行速度及攻角。研究EFP的氣動外形有利于提高飛行過程中的穩定性及精度。

彈丸在空氣中飛行時，彈軸與速度的夾角稱為攻角，攻角所在的平面稱為阻力面，如圖5所示，以彈丸質心為坐標原點建立右手笛卡爾坐標系oxyz，ox軸與彈丸速度方向相反，oy軸在阻力面內且與ox垂直，oz軸則與阻力平面垂直。作用在彈丸P點上的空氣動力R在ox軸方向上的投影為Rx，稱之為正面阻力；在oy軸方向上的投影為Ry，稱之為升力；在oz軸上的投影為Rz，稱之為側向力。彈丸都會有正面阻力，如有攻角還會產生升力。

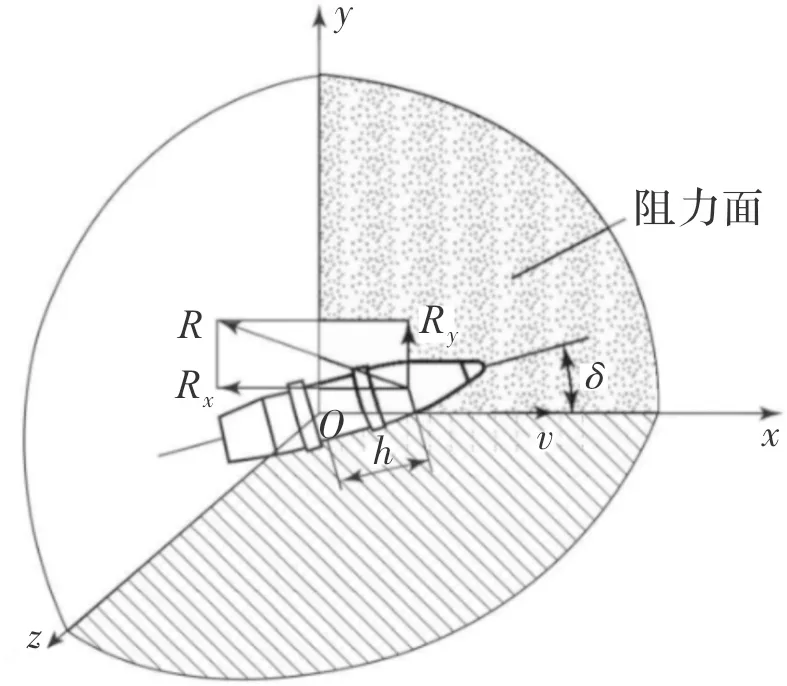
圖5 作用在彈丸上的空氣動力

根據空氣動力學規定，上述空氣動力可以表示為：

(1)

式中：p為空氣密度；S為彈丸最大橫截面面積；v為彈丸飛行速度；Cx為正面阻力系數；Cy為升力系數；Cz為側向力系數。

若壓心P在彈丸頭部與質心之間，此時升力與正面阻力的合力引起彈丸質心偏轉的力矩Mz稱之為翻轉力矩，若壓心在彈底與質心之間則力矩Mz稱之為穩定力矩。EFP的穩定性通常用穩定儲備量B來表示。即：

(2)

式中：xp，Cp分別為彈丸阻力中心至彈頂的絕對、相對距離；xs，Cs分別為彈丸質心至彈頂的絕對、相對距離；l為彈丸全長。

對于尾翼穩定的彈丸，應盡量使空氣動力對彈丸質心的力矩為穩定力矩，及B>0，良好的尾翼穩定彈丸，其穩定儲備量至少在15%～28%。穩定儲備量是決定彈丸能否以預設攻角到達瞄準點的一個重要參量。

3 計算結果及分析

3.1 不同起爆半徑對EFP成形的影響

多點起爆時，在爆轟發生的一瞬間，每一個起爆點所引起的爆轟以球面波的形式傳播，隨著爆轟波的傳播，相鄰位置的爆轟波會在其對稱面位置上相遇，并發生激烈碰撞，形成馬赫波。在爆轟碰撞區域內壓力增加，炸藥爆轟更加完全，相當于增加了炸藥爆轟的局部能量釋放。在藥型罩與馬赫波接觸的微元上，壓力會比附近微元高，離馬赫區越遠，其藥型罩上的壓力也會隨之降低，正是由于藥型罩表面微元上的這種壓力梯度的變化，導致折疊尾翼的形成。多邊形殼體對尾翼的形成也有一定的增益作用。表1是多點起爆下EFP成型增益情況，EFP的平均速度增益、長徑比增益都是對單點起爆而言。

表1 各起爆方式下EFP的參數

3.2 起爆半徑和攻角對阻力系數的影響

圖6展示了4種EFP的阻力系數隨攻角的變化曲線。

圖6 阻力系數變化曲線

在確定攻角時，隨著起爆半徑的增加，阻力系數急劇降低。分析其主要原因是起爆半徑增大導致了EFP長徑比增大，相應的受力橫截面積減小，因此減小了阻力，導致阻力系數降低；在確定起爆半徑條件下，隨著攻角的增加，其阻力系數會增加。分析其原因是存在攻角時彈丸的迎風面積會顯著增大，導致其阻力增大。

3.3 起爆半徑和攻角對升力系數的影響

圖7展示4種不同起爆半徑下的EFP的升力系數隨攻角的變化規律。

圖7 升力系數變化曲線

在確定攻角時，其起爆半徑越大，升力系數越大，這是由于起爆半徑增大導致彈丸長徑比增加，EFP的馬赫數更高，作用在彈丸外表面迎風側和被風側的氣壓差值更大，所以其造成的升力更大，而其彈丸最大橫截面積卻隨著起爆半徑的增大而減小。因此升力系數會隨著起爆半徑的增加而增加；起爆半徑相同時，隨著攻角δ的增加，EFP升力系數呈線性增加，其斜率與起爆半徑呈正相關，攻角δ>15°以后，其升力系數增加速度減緩，甚至隨著攻角的增加其升力系數開始下降。

3.4 起爆半徑和攻角對穩定儲備量的影響

穩定儲備量是描述尾翼穩定彈丸飛行穩定性的一個重要參量。圖8展示了各侵徹體的穩定儲備量隨攻角的變化曲線。

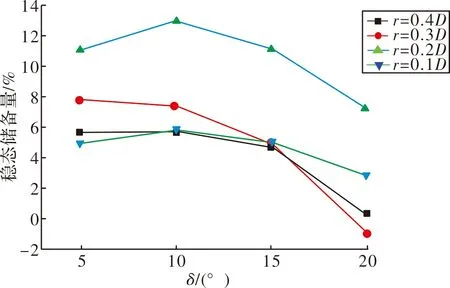
圖8 穩定儲備量變化曲線

在δ<15°時，隨著起爆半徑的增加，穩定儲備量會有一個先上升后下降的趨勢，穩定儲備量對攻角的變化不太敏感；在δ>15°時，穩定儲備量會急劇下降，彈丸飛行穩定性會明顯降低，這會對彈丸的著靶姿態產生不利影響，從而影響彈丸的終點效應。因此尾翼穩定飛行EFP的攻角應該嚴格的控制在一個合理范圍內。

3.5 EFP威力特性綜合分析

影響EFP威力的主要因素有長徑比、氣動特性、速度及速度保存能力。由以上分析可知，在幾種不同起爆半徑下EFP的速度隨起爆半徑的增加而增大，且其增長率逐漸減小，尤其是起爆半徑r=0.4D與r=0.3D相比，其速度增加僅為0.4%，因此當起爆半徑增加到0.3D以上時，僅僅增加的是EFP的長徑比,而對EFP的速度增益并不明顯。EFP威力重要評價指標之一是開孔直徑。因此長徑比不宜過大。然而長徑比越大，其速度保存能力就越強，但其靜態儲備量會下降從而影響彈丸的飛行穩定性，靜態儲備量與阻力系數及彈丸速度這幾個因素相互制約，因此應該對其綜合考慮。從前面的分析可以看出，起爆半徑r位于0.2D～0.3D之間時，EFP的靜穩定儲備最大，而其阻力系數及EFP的速度都控制在一個較為理想的范圍內。

4 結論

采用LS-DYNA對不同起爆半徑下的EFP進行數值模擬，并通過Fluent分別計算不同攻角時的阻力系數、升力系數、靜穩定儲備量等氣動參數，得出如下結論：

1)通過UG逆向建模將LS-DYNA計算得到的EFP外形數據傳遞給流體力學計算軟件Fluent進行超高音速氣動分析，實現了LS-DYNA與Fluent的聯合仿真。

2)通過Fluent氣動分析，綜合考慮阻力系數、穩定儲備量及彈丸速度，確定了成型彈丸6點起爆，起爆半徑r位于0.2D～0.3D內時能夠獲取更好實現其終點效應的侵徹體。