基于NARX神經網絡的火箭炮發火回路狀態預測研究

王小召，張建新，張 震，李永保，李 鋒，謝立中

(湖北江山重工有限責任公司，湖北襄陽 441005)

0 引言

在未來的信息化戰爭中，保障行動對整個作戰體系的支撐作用至關重要。作戰方式的多樣性對保障的時效性和精確性提出更高的要求[1]。武器裝備的智能故障診斷和預測是實現預知維修和自主式保障的重要手段[2]。

神經網絡具有極強的非線性映射能力，在故障預測方面受到廣泛關注。動態神經網絡對過程或工況參數建立動態模型，輸出不僅依賴當前的輸入，還與當前和過去的輸入、輸出有關。其中，NARX(nonlinear autoregressive network with exogenous inputs)神經網絡性能優越，是非線性動態系統中應用最廣泛的一種神經網絡[3]。

目前，針對火箭炮狀態預測的研究較少，文獻[4]采用Elman神經網絡針對時間序列的內在特性對防空火箭炮交流伺服系統的速度量進行了預測，但沒有考慮其它外在因素的影響。由于服役條件復雜多變，火箭炮狀態受環境、振動、沖擊等多種因素的影響。基于NARX神經網絡引入模糊理論，提出了將多種外部輸入的影響因素進行綜合評分，以綜合評分作為NARX神經網絡的外部輸入量的預測方法。通過對比分析，該方法能夠在保證預測精度滿足要求的前提下，使得NARX神經網絡的規模減小、收斂速度提高，同時提高了NARX神經網絡對火箭炮發火回路狀態變化趨勢的預測精度。

1 火箭炮發火回路

1.1 關鍵要素

火箭炮發火系統用于點燃火箭發動機的發火藥，將火箭彈按指令要求的順序和間隔發射出去。

根據收集的歷史故障數據對某型火箭炮火控系統故障進行統計分析，結果如圖1所示，發火回路故障數量最多，占火控系統總故障數的37.5%。發火回路的主要故障模式為斷路、電阻值過高或過低等。

圖1 火控系統故障分布

回路電阻主要反映的是發火回路的連接狀態，直接關系到火箭炮能否對火箭彈進行可靠發射[5]；因此，將回路電阻作為發火回路狀態的表征量是合理的。

回路電阻的主要影響因素從兩個方面考慮：一方面是介質自身物理特性，除與介質自身的組成有關外，還與所處的環境有關，主要包括溫度、濕度等[6]；另一方面是接插件的接觸電阻，主要受振動強度、振動時間、外力和環境中的溫度、濕度、鹽霧等的影響。外力是指工作額定載荷之外的破壞力，是不可預知的、偶然的。因此，對于陸軍裝備某型火箭炮來說，溫度、濕度和振動情況是影響回路電阻的主要因素。

1.2 狀態數據

在試驗室模擬火箭炮工作環境，對發火回路進行不同溫度和濕度條件下的振動試驗，利用歐姆表檢測回路電阻。溫度范圍為：-40～+50 ℃，相對濕度范圍為：20%～95%，取不同溫度和濕度的組合共17組，見表1。

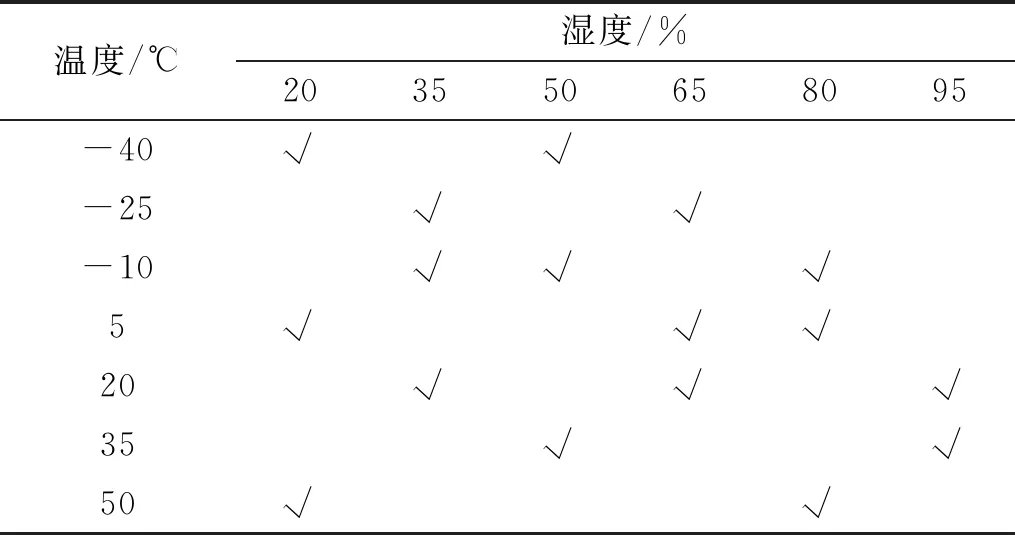
表1 溫度和濕度取值表

振動試驗在振動試驗臺上進行，試驗量值如圖2所示，掃頻速度不大于1 oct/min(從5 Hz升至200 Hz再降至5 Hz對數掃頻)，振動方向為X，Y，Z三個方向，每個方向振動12 min為一個振動周期。

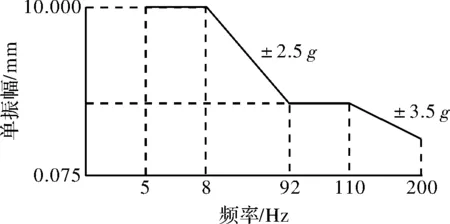
圖2 正弦掃描振動試驗曲線

試驗過程如下：

1)取表1中的一組溫度和濕度值，設定試驗室溫度和濕度；

2)將發火回路放置在試驗室4 h；

3)將發火回路放置在振動試驗臺上，按要求振動3個周期；

4)用歐姆表測量回路電阻；

5)記錄溫度、濕度、振動時間和回路電阻試驗數據。每個振動周期等間隔記錄3組數據，每組環境參數記錄9組數據。

2 模糊綜合評判

2.1 影響因素及權重

發火回路阻值的影響因素集記為U={溫度,濕度,振動時間}。采用相對劣化度的分析方法對各影響因素參數進行歸一化處理[7]，其中溫度和振動時間按越小越優型參數處理；濕度按中間型參數處理，參數范圍取[20%,95%]，最佳運行范圍取[50%,70%]。

采用客觀賦值法中的相關系數法計算權重[8]，形成權重向量A。經對生產過程中試驗檢測數據的統計分析，對應影響因素溫度、濕度和振動時間，權重向量取A=[0.113,0.208,0.679]。

2.2 隸屬度

將各因素的優劣狀態劃分為l1，l2，l3，l4四個評價等級，分別表示優、良、中、差，即等級集L={l1,l2,l3,l4}。選取梯形分布[9]來計算各個因素對各個評價等級的隸屬度，形成隸屬度矩陣R，隸屬度函數曲線如圖3所示。

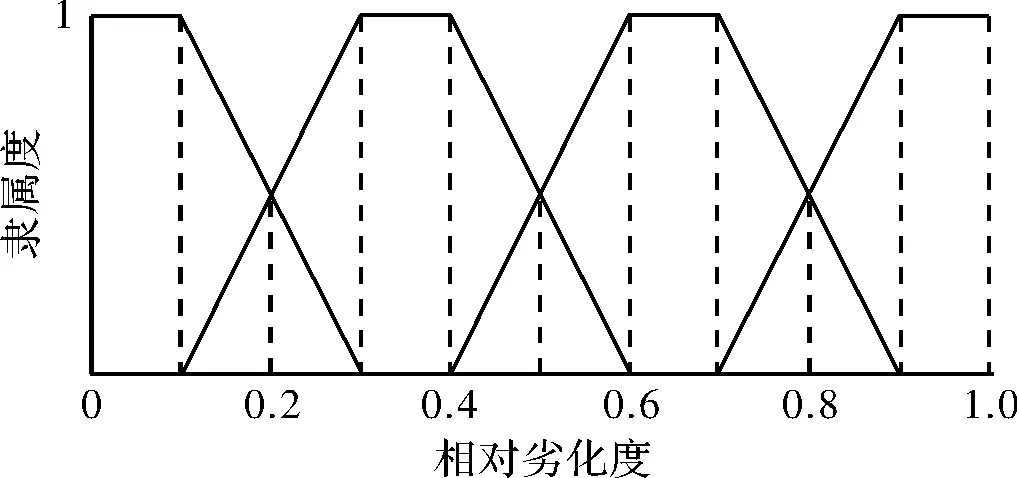
圖3 隸屬度函數曲線

2.3 模糊綜合評判

因素權重向量A和隸屬度矩陣R確定后，即可得到綜合評價矩陣B：

B=A°R=[b1,b2,b3,b4]

(1)

其中，“°”為模糊算子，采用M(·,+)進行運算。

對影響因素進行綜合評價的目的是獲得各影響因素共同產生的綜合影響的量化值。因此，借鑒文獻[10]的方法，對等級集L中的每個等級給予一個相應的分值構成分值向量C=[1,4,8,16]。最后，可得到各影響因素的綜合評分值：

ε=BCT

(2)

3 NARX神經網絡預測模型

3.1 NARX神經網絡原理

典型的NARX神經網絡結構如圖4所示，主要包括輸入層、隱含層和輸出層，其中輸入層含有兩個延時環節。

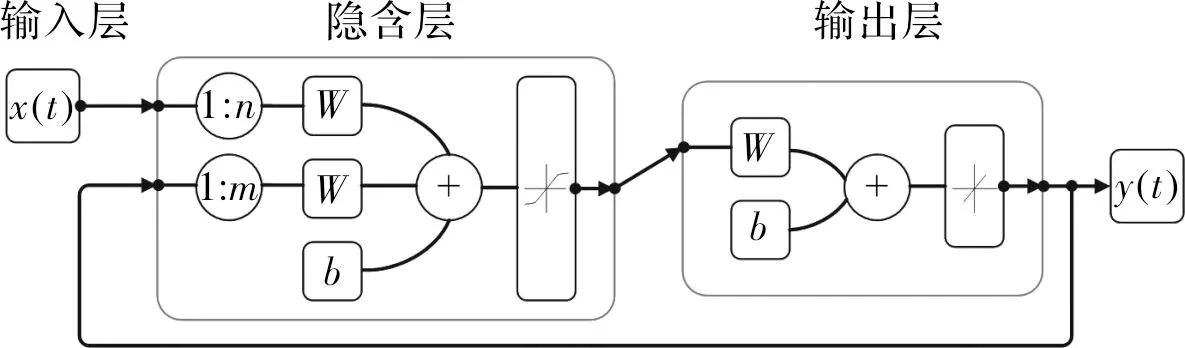
圖4 NARX神經網絡結構圖

在圖4中，外部輸入變量x(t)的延時長度為n，輸出變量y(t)的反饋延時長度為m。一般情況下，輸出層只包含一個輸出變量y(t)，假設外部輸入變量x(t)包含多個輸入信號xi(t)，i=1,2,…,k，則NARX神經網絡的數學模型為：

y(t)=f(y(t-1),y(t-2),…,y(t-m),x1(t-1),x1(t-2),…,x1(t-n),…,xk(t-1),xk(t-2),…,xk(t-n))

(3)

與BP靜態神經網絡相比，NARX神經網絡增加了從輸出到輸入的反饋連接，包含外部輸入量和輸出量的時間序列，具有豐富的歷史信息和優秀的動態性能，能夠很好地逼近非線性動力學模型[11]。

3.2 狀態預測模型

采用上述模糊綜合評判法對每組影響因素進行評判，形成綜合評分值序列。建立單輸入單輸出的NARX神經網絡模型A，將綜合評分值序列作為外部輸入變量，將對應的回路阻值序列作為輸出變量。

作為對比，建立三輸入單輸出的NARX神經網絡模型B，將溫度、濕度和振動時間3個序列作為外部輸入變量，將對應的回路阻值序列作為輸出變量。

NARX預測模型的流程圖如圖5所示。

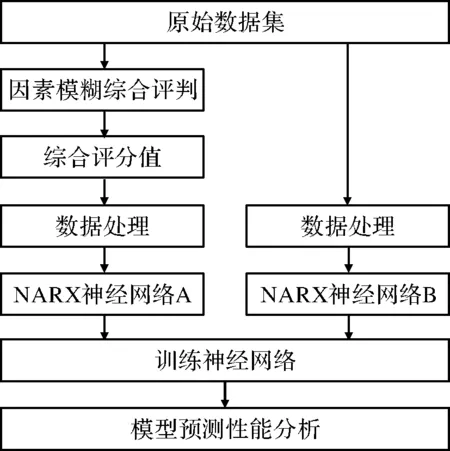
圖5 NARX預測模型流程圖

3.3 評價指標

為了評價模型，將預測值yi和實際值hi之間的均方誤差(MSE)和相關系數r作為預測精度的評價指標。

MSE表達式為：

(4)

MSE越接近0，說明兩個變量的偏差越小，r的表達式為：

(5)

|r|越接近1說明變量之間的線性相關程度越高，為了評價模型的訓練速度，將迭代次數作為評價指標。

4 預測分析

4.1 數據處理

為了降低數據量級的影響，提高神經網絡的收斂速度，將輸入和輸出數據歸一化至[0,1]范圍，數據處理表達式為：

(6)

其中：xi為需要處理的原始數據；xmax和xmin分別為變量x數據中的最大值和最小值。

4.2 參數設置

利用1.2節獲得的153組樣本數據中的前140組數據對神經網絡模型A和模型B進行訓練，其中70%作為訓練數據，15%作為校驗數據，15%作為測試數據。

神經網絡模型A和模型B訓練算法均采用魯棒性高且收斂速度快的LM算法。

采用試湊法確定兩神經網絡模型的隱含節點數和延時長度：首先固定延時長度，然后不斷調整隱含節點數，測試不同模型的性能；之后固定隱含節點數，不斷改變延時長度[12]。經試驗后確定模型A的隱含節點數為4，延時長度為2；模型B的隱含節點數為12，延時長度為2。

4.3 結果及分析

神經網絡經過反復訓練達到預期要求后，分別利用模型A和模型B對153組樣本數據中的后13組數據進行發火回路阻值預測，預測結果如圖6和表2所示。

圖6 預測結果對比圖

表2 NARX神經網絡預測結果表

從單個預測點來看，NARX神經網絡對發火回路阻值的預測精度較高，兩模型對各點的預測誤差均在1%以內。從整體看，模型A和模型B的預測結果和實際值的均方誤差分別為4.37×10-5和5.54×10-5，模型A的預測精度略大于模型B；從變化趨勢上看，兩模型均能較好的預測發火回路阻值的變化趨勢，模型A和模型B的預測結果和實際值的相關系數分別為0.996和0.993。由于模糊綜合評判對影響因素的影響進行了模糊化，影響因素的綜合評分對影響因素變化的敏感度降低，相對于單個影響因素而言變化更加平緩，因而模型A在對發火回路阻值變化趨勢的預測上略優于模型B。

為了減小數據劃分情況和權重初始值對訓練過程及結果的影響，在劃分訓練數據和初始化權重參數時采用隨機的方式，分別對模型A和模型B訓練20次，得到均方誤差和迭代次數的平均值，見表3。

表3 神經網絡評價指標對比表

根據表3，由隱含節點數來看，模型A的規模較小，這是由于對影響因素的模糊綜合評判使得外部輸入減少，模型得到簡化；由均方誤差來看，NARX神經網絡能夠對火箭炮發火回路阻值的訓練數據進行擬合且精度均較高，模型A的預測精度略高于模型B；由迭代次數來看，模型A的收斂速度較快。

5 結束語

針對火箭炮服役環境變化劇烈和影響因素復雜等特點，基于NARX神經網絡的優良動態性能和非線性擬合能力，引入模糊理論，將模糊綜合評判法和NARX神經網絡結合，提出了對影響因素進行綜合評分后，以綜合評分作為NARX動態神經網絡的外部輸入量，對火箭炮狀態進行預測的方法，以某型火箭炮發火回路為例，進行試驗對比。結果表明，經過對影響因素的模糊綜合評分，NARX神經網絡的規模減小且收斂速度更快，對狀態變化趨勢的預測也更加精確。