深部硐室長(zhǎng)期穩(wěn)定性的兩個(gè)力學(xué)問(wèn)題*

王明洋，徐天涵，鄧樹(shù)新，陳昊祥

（1. 中國(guó)人民解放軍陸軍工程大學(xué)爆炸沖擊防災(zāi)減災(zāi)國(guó)家重點(diǎn)實(shí)驗(yàn)室，江蘇 南京 210007；2. 南京理工大學(xué)機(jī)械工程學(xué)院，江蘇 南京 210094；3. 北京建筑大學(xué)北京交通基礎(chǔ)設(shè)施建設(shè)國(guó)際合作基地，北京 100044）

深部硐室圍巖的長(zhǎng)期強(qiáng)度與變形問(wèn)題不僅是巖石力學(xué)的基本問(wèn)題，也是當(dāng)前我國(guó)諸如川藏鐵路交通、水電水利、能源礦山和國(guó)防軍事防御等重大工程，乃至地球物理及高能物理科學(xué)實(shí)驗(yàn)等基礎(chǔ)設(shè)施深地下化建設(shè)中亟待弄清的問(wèn)題。該問(wèn)題的復(fù)雜性不僅在于深部非均勻裂隙巖體中存在高封閉應(yīng)力且難以確定影響裂隙介質(zhì)變形與強(qiáng)度的主要因素，還在于如何在巖體大變形及破壞情況下表征其固有屬性。陳宗基院士早在20 世紀(jì)60 年代就已充分認(rèn)識(shí)到巖體變形由巖塊中的巖石介質(zhì)變形和巖塊邊界面（結(jié)構(gòu)面）附近區(qū)域以及巖體的弱化區(qū)（裂縫處）的變形組成，并基于流變學(xué)原理系統(tǒng)開(kāi)展了巖體變形與強(qiáng)度特征的理論與實(shí)驗(yàn)研究；80 年代，他結(jié)合地球動(dòng)力學(xué)、構(gòu)造地質(zhì)學(xué)和流變學(xué)方法，開(kāi)創(chuàng)性地進(jìn)行了巖體中封閉應(yīng)力形成與釋放、巖體隨時(shí)間的強(qiáng)度變化與擴(kuò)容、以及地下硐室圍巖位移等現(xiàn)象的力學(xué)機(jī)理研究。強(qiáng)調(diào)了地應(yīng)力（構(gòu)造應(yīng)力）在裂隙塊狀巖體運(yùn)動(dòng)以及不穩(wěn)定漸進(jìn)破裂中起著基本作用的觀點(diǎn)。這些觀點(diǎn)體現(xiàn)在有關(guān)巖石流變、回彈、松動(dòng)、擴(kuò)容以及長(zhǎng)期強(qiáng)度等基本概念中，對(duì)認(rèn)識(shí)地下硐室圍巖長(zhǎng)期穩(wěn)定性與地質(zhì)構(gòu)造非協(xié)調(diào)變形和封閉應(yīng)力相互作用的力學(xué)機(jī)理以及相關(guān)防控措施至關(guān)重要[1-5]。

在長(zhǎng)期的地質(zhì)活動(dòng)作用下，深部巖體內(nèi)部存在大量的斷層、節(jié)理、裂隙等缺陷，它們將巖體分割成大小、形狀不一的塊體。巖體中裂縫的寬度可從構(gòu)造斷裂的百米級(jí)到微裂紋與礦物晶粒缺陷的10?8m，裂縫的延展長(zhǎng)度可從106m 到10?6m，即從宏觀斷裂尺度到細(xì)觀和微觀裂紋尺度[6]。地質(zhì)力學(xué)與地球物理領(lǐng)域不斷發(fā)展的實(shí)驗(yàn)研究驗(yàn)證了Sadovsky 院士及其學(xué)派提出的巖體等級(jí)構(gòu)造觀點(diǎn)的正確性[7-10]。Sadovsky 院士[7]認(rèn)為實(shí)際巖體可表示為由遵從等級(jí)序列的構(gòu)造單元組成的集合體（塊體），這些塊體由軟弱區(qū)隔開(kāi)。構(gòu)造單元邊界可以是張開(kāi)（未填充）的斷層，也可以是部分填充的裂縫等不連續(xù)構(gòu)造。在任何情況下，任意構(gòu)造等級(jí)的巖體介質(zhì)都可以表示成體積為Vi（i=1,2,···,N，其中N為等級(jí)劃分的最深層次）的塊體的集合體，這些塊體具有不同的物理力學(xué)性質(zhì)。

利用巖體中的間斷尺度來(lái)對(duì)介質(zhì)構(gòu)造單元進(jìn)行等級(jí)排列。假設(shè)最大的構(gòu)造塊為0 級(jí)塊體，則組成0 級(jí)塊體的構(gòu)造單元由0 級(jí)塊體中最大的間斷劃分，并被稱(chēng)作1 級(jí)塊體（i= 1），依此類(lèi)推（見(jiàn)圖1）。在這樣的巖體介質(zhì)中，每一個(gè)單元都可以被賦予等級(jí)i（i=1,2,···,N）。

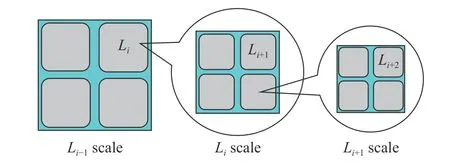
圖1 巖體的構(gòu)造等級(jí)示意圖Fig. 1 Sketch of hierarchical structure of rock blocks

按此定義，含有i+1,i+2,···,N級(jí)構(gòu)造塊體的集合體組成了i級(jí)塊體內(nèi)部的獨(dú)立構(gòu)造塊，而i級(jí)塊體又是i? 1 級(jí)塊體的從屬單元。

上述巖體等級(jí)構(gòu)造模型包括了所有等級(jí)的塊體以及其中的軟弱區(qū)域（不同等級(jí)塊體之間的間隔），而且在每一個(gè)集合體中任意區(qū)域介質(zhì)是非常不均勻的，這些區(qū)域包含了巖塊，更高級(jí)塊體的集合，或塊體之間的間隙。

按照巖體構(gòu)造等級(jí)這一學(xué)說(shuō)，自然界中的巖體，大到大陸板塊，小到細(xì)砂顆粒，甚至是晶體的結(jié)構(gòu)單元，都具有嵌入特性或者層次重復(fù)性，在大的部分中嵌入小的部分，而后者又有更小的部分嵌入。然而，目前在研究巖體自然變形或誘發(fā)變形時(shí)，常把巖體看作為各向同性的連續(xù)體，因而巖體的應(yīng)力應(yīng)變狀態(tài)以及力學(xué)過(guò)程廣泛采用連續(xù)介質(zhì)力學(xué)的數(shù)學(xué)模型描述（例如，彈性、塑性、蠕變、脆性和韌性斷裂等概念）。其不足之處在于無(wú)法有效表征對(duì)應(yīng)不同結(jié)構(gòu)層次的空間及時(shí)間規(guī)模上巖體發(fā)生的變形及破壞過(guò)程，因此也就無(wú)法解釋含能巖體的許多非線性力學(xué)現(xiàn)象[11-12]。這些非線性力學(xué)現(xiàn)象包括：

（1）在不同結(jié)構(gòu)尺寸級(jí)別上發(fā)生著程度不同的塊體運(yùn)動(dòng)。如Kocharyan 等[13]對(duì)地下核試驗(yàn)的場(chǎng)地效應(yīng)調(diào)查發(fā)現(xiàn)，在距離爆炸較遠(yuǎn)處的地下硐室周?chē)小皦K體激活”現(xiàn)象，小型巖塊（尺度為10?1～100m）的穩(wěn)定可以通過(guò)工程措施來(lái)保證，而大型巖塊（尺度為101～102m）的穩(wěn)定無(wú)法通過(guò)工程措施實(shí)現(xiàn)。

（2）在工程級(jí)別的規(guī)模上發(fā)生著自然以及人為成因的微地震、巖爆等動(dòng)力現(xiàn)象[14-15]。如在深地下進(jìn)行大規(guī)模爆破時(shí)，距離爆源較遠(yuǎn)處的巖體即使經(jīng)過(guò)幾個(gè)小時(shí)甚至幾天后也有可能出現(xiàn)巖爆、工程地震等災(zāi)害。顯然這是由于擾動(dòng)作用導(dǎo)致巖體約束解除，內(nèi)部?jī)?chǔ)存能量釋放的結(jié)果[16]。

（3）硐室圍巖破壞區(qū)在時(shí)間與空間上呈現(xiàn)漸進(jìn)發(fā)展模式。錦屏一級(jí)電站主廠房洞周?chē)鷰r的松動(dòng)區(qū)隨著開(kāi)挖深入，從最初2 m 發(fā)展到最大17 m 以上，并且沿徑向深度呈現(xiàn)間隔性分布[17-20]。白鶴灘電站右岸廠房巖體內(nèi)部8.5 m 深度處，由于應(yīng)力轉(zhuǎn)移出現(xiàn)新生破裂，并且破裂面在一年多內(nèi)不斷擴(kuò)展[21]。

（4）在實(shí)驗(yàn)室規(guī)模上發(fā)生由巖樣內(nèi)部能量釋放引起的微細(xì)觀裂紋的產(chǎn)生、發(fā)展與宏觀破壞，以及擴(kuò)容現(xiàn)象。如Revuzhenko[22]從深部巖體中取出的完整巖樣，在靜置一段時(shí)間后能自發(fā)快速崩解。若在完整巖樣的表面刻痕或輕微敲擊，則會(huì)加速其破壞過(guò)程。再如對(duì)深部巖樣施加軸壓后卸載，試樣的高度與直徑均會(huì)隨著時(shí)間的推移而逐漸增大。顯然這些現(xiàn)象中巖樣破壞與擴(kuò)容所做的功來(lái)源于內(nèi)部?jī)?chǔ)存的能量。

巖體固有的非均勻構(gòu)造與封閉應(yīng)力特性是產(chǎn)生上述現(xiàn)象最本質(zhì)的原因。尤其對(duì)于賦存在高地應(yīng)力有勢(shì)場(chǎng)環(huán)境中的深部巖體，在掘進(jìn)、爆炸以及地震等擾動(dòng)作用下，隨著不同尺度水平上應(yīng)力場(chǎng)的不均勻性增加，該固有特性作用更加突出。雖然非均勻介質(zhì)中多尺度、多階段變形破壞的定量計(jì)算方法已取得長(zhǎng)足進(jìn)步，但由于巖體的實(shí)際構(gòu)造特征有眾多的初始條件，目前在計(jì)算上仍存在困難。如果將非均勻巖體的變形看成強(qiáng)烈非平衡系統(tǒng)，按照非均勻系統(tǒng)行為的統(tǒng)計(jì)物理規(guī)律，僅研究具有耗散的宏觀結(jié)構(gòu)單元變形行為，則問(wèn)題可得到極大簡(jiǎn)化。

本文中利用Sadovsky 院士關(guān)于復(fù)雜地質(zhì)巖體的等級(jí)構(gòu)造學(xué)說(shuō)，圍繞深部巖體非均勻構(gòu)造與封閉應(yīng)力固有的統(tǒng)計(jì)力學(xué)屬性，沿著陳宗基院士關(guān)于地下硐室長(zhǎng)期穩(wěn)定性力學(xué)問(wèn)題方向，在作者相關(guān)研究基礎(chǔ)上[23-25]，研究巖體固有的非均勻構(gòu)造與封閉應(yīng)力特性，以及初始地應(yīng)力對(duì)硐室圍巖長(zhǎng)期穩(wěn)定性影響的機(jī)制與破壞準(zhǔn)則這兩個(gè)問(wèn)題。

1 巖體非均勻構(gòu)造的固有力學(xué)問(wèn)題

1.1 巖體非均勻構(gòu)造的變形特征

巖體的變形特性是其最基本的性質(zhì)，這些特性由兩方面決定：一是由其組成部分（次級(jí)塊體及其間隙）的變形及強(qiáng)度特征參數(shù)決定，二是由其整體的變形特征參數(shù)決定。根據(jù)外部作用大小不同，集合體構(gòu)造單元的變形可以是協(xié)調(diào)的，也可以是不協(xié)調(diào)的。由此，集合體的狀態(tài)在某一時(shí)刻可以是密合的，也可以是非密合的。如果在變形的初始階段所有構(gòu)造等級(jí)的構(gòu)造單元處于密合狀態(tài)（見(jiàn)圖2（a）），那么，根據(jù)流變學(xué)的概念，可以劃分出非均勻介質(zhì)的三個(gè)變形階段。

（1）可逆變形階段（見(jiàn)圖2（b））。該階段構(gòu)造單元的所有組成部分的變形均處于彈性極限內(nèi)，介質(zhì)仍保持其連續(xù)性。在外部加載解除后介質(zhì)返回到初始狀態(tài)。

（2）不可逆協(xié)調(diào)變形階段（見(jiàn)圖2（c））。在該階段，塑性非協(xié)調(diào)變形區(qū)域形成，但是沒(méi)有破壞介質(zhì)的連續(xù)性，在較低強(qiáng)度構(gòu)造單元上形成的塑性非協(xié)調(diào)性可由其他區(qū)段的彈性變形來(lái)補(bǔ)償。這時(shí)產(chǎn)生的內(nèi)部應(yīng)力在外部荷載解除后仍然存在。

（3）非協(xié)調(diào)變形階段（見(jiàn)圖2（d））。當(dāng)彈性變形不足以補(bǔ)償塑性變形時(shí)，不可逆變形使構(gòu)造單元失去連續(xù)性，該構(gòu)造單元在一個(gè)或多個(gè)軟弱面上發(fā)生斷裂，進(jìn)而產(chǎn)生旋轉(zhuǎn)與平移。應(yīng)當(dāng)注意到，n級(jí)構(gòu)造單元上非連續(xù)性的出現(xiàn)使其整體變形得以部分恢復(fù)，這導(dǎo)致在n?1 級(jí)構(gòu)造單元（尺度更大的塊體）中出現(xiàn)非協(xié)調(diào)性變形所需的應(yīng)變更大，即出現(xiàn)時(shí)間滯后效應(yīng)。

圖2 第n 級(jí)非均勻構(gòu)造單元的變形階段Fig. 2 The deformation stages of the nth non-uniform structure

如上所述，隨著外力作用的強(qiáng)度增加，微觀水平上應(yīng)力場(chǎng)的不均勻性不斷增加。根據(jù)非均勻系統(tǒng)統(tǒng)計(jì)物理規(guī)律，必然形成與外力作用相應(yīng)的耗散結(jié)構(gòu)，并且耗散結(jié)構(gòu)的線性尺寸L?對(duì)應(yīng)于巖體中的自然巖塊尺度。如果外力作用引起的變形不超過(guò)臨界值 ε?，那么不可逆變形就不會(huì)發(fā)生。在塊系介質(zhì)中最大變形發(fā)生在軟弱面附近，因此應(yīng)變可按 ε =U0/L?計(jì)算，其中U0為鄰近塊體面之間的相對(duì)位移。文獻(xiàn)[26]中給出了 ε?的計(jì)算方法，其中把現(xiàn)實(shí)的巖體看成是時(shí)變的非平穩(wěn)系統(tǒng)，根據(jù)地構(gòu)造運(yùn)動(dòng)中積累的眾多資料得出 ε?=(1 ～2)×10?5。需要注意的是，破壞時(shí)的應(yīng)變一般為10?4，這也就意味著巖體在產(chǎn)生不可逆變形之后，到發(fā)生破壞之前，仍能產(chǎn)生一定的應(yīng)變。

1.2 巖體非均勻構(gòu)造的封閉應(yīng)力

式中：< >表示對(duì)體積V的平均。

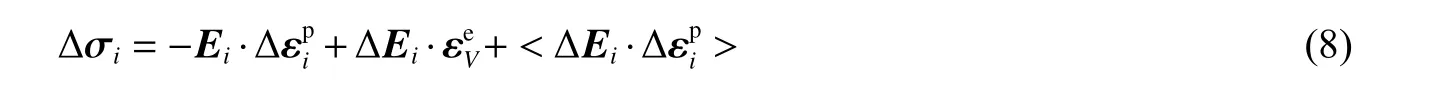
式(9)表明，非均勻介質(zhì)變形時(shí)產(chǎn)生的塑性協(xié)調(diào)變形，在外力卸載后將導(dǎo)致殘余內(nèi)應(yīng)力的產(chǎn)生，其大小和狀態(tài)（包括殘留應(yīng)力值）不僅由變形增降確定，也由所考察的構(gòu)造集合體中單獨(dú)區(qū)段的變形模量差值?E i所確定，?E i可以看作是介質(zhì)具體區(qū)段的缺陷程度。

巖體的封閉應(yīng)力特性對(duì)深部圍巖的長(zhǎng)期穩(wěn)定有兩個(gè)重要影響：

（1）巖塊單元在外載徹底卸去后，單元內(nèi)部可能出現(xiàn)局部的拉應(yīng)力，造成單元的拉伸破壞，這一特性對(duì)深部圍巖的變形破壞形態(tài)具有重要影響[28-29]；

（2）巖塊單元在外載徹底卸去后很大一部分能量還保存下來(lái)，在爆破或地震等動(dòng)力擾動(dòng)作用下，這部分儲(chǔ)存的能量可以釋放，既能緩慢釋放，也可快速釋放，巖體的這一特性非常顯著地影響著圍巖動(dòng)力的穩(wěn)定性[30-32]。

2 深部硐室圍巖的長(zhǎng)期變形問(wèn)題

深部硐室圍巖長(zhǎng)期穩(wěn)定的防控技術(shù)，本質(zhì)上是為了防止硐室鄰近區(qū)圍巖因蠕變或破碎而引起的坍塌作用。深部硐室開(kāi)挖后圍巖的向內(nèi)收斂會(huì)在支護(hù)結(jié)構(gòu)上產(chǎn)生數(shù)百甚至數(shù)千噸每平方米的壓力，支護(hù)結(jié)構(gòu)必須在沒(méi)有斷裂的情況下承受位移，顯然，“剛性”支護(hù)會(huì)因難以承受這些位移而斷裂。因此，深部硐室圍巖長(zhǎng)期變形（長(zhǎng)期變形狀態(tài)下的位移）的定量評(píng)估是長(zhǎng)期穩(wěn)定支護(hù)體系設(shè)計(jì)的基礎(chǔ)。

研究靜水壓力狀態(tài)下大深度圓形水平硐室圍巖的變形破壞問(wèn)題時(shí)，硐室可簡(jiǎn)化為軸對(duì)稱(chēng)問(wèn)題，選用柱坐標(biāo)系（r，θ，z），即取主應(yīng)力σr沿徑向坐標(biāo)、σθ沿切向坐標(biāo)、σz沿軸向坐標(biāo)。在工作面掘進(jìn)過(guò)程中，工作面附近的徑向應(yīng)力σr減小到零，切向應(yīng)力σθ的變化取決于介質(zhì)變形性質(zhì)（見(jiàn)圖3，應(yīng)力狀態(tài)隨時(shí)間而變化）。對(duì)于長(zhǎng)坑道，一般認(rèn)為σz的變化不大，因此硐室的變形可看作是平面應(yīng)變問(wèn)題（ε0z=0）。在上述條件下，地下圓形硐室圍巖最大剪切應(yīng)力為τ=(σθ?σr)/2，當(dāng)σ0≥τmax（其中σ0為初始地應(yīng)力，τmax為巖石的剪切強(qiáng)度極限）時(shí)，由經(jīng)典彈塑性理論可知硐室圍巖出現(xiàn)塑性區(qū)，一般認(rèn)為此時(shí)初始地應(yīng)力對(duì)應(yīng)的埋深即為硐室位于“深部”的臨界深度。

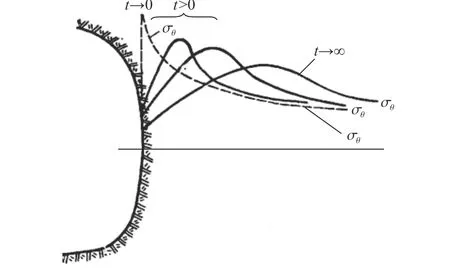
圖3 硐室開(kāi)挖前后側(cè)墻圍巖應(yīng)力狀態(tài)的變化[1]Fig. 3 The change of stress state of surrounding rocks before and after the tunneling[1]

隨著埋深進(jìn)一步增加，硐室圍巖狀態(tài)逐漸向復(fù)雜圍巖應(yīng)力應(yīng)變狀態(tài)過(guò)渡。這種過(guò)渡與圍巖產(chǎn)生的非彈性變形和破裂有關(guān)，在過(guò)渡中出現(xiàn)峰值后巖體的非線性特性，其中主應(yīng)力之間的比例和主方向都可能發(fā)生變化，此時(shí)對(duì)剪切強(qiáng)度的評(píng)估非常重要。因此，研究硐室周?chē)膽?yīng)力應(yīng)變狀態(tài)就意味著研究巖體的剪切強(qiáng)度。

2.1 深部硐室圍巖的剪切強(qiáng)度與破壞準(zhǔn)則

2.1.1 Coulomb-Mohr 強(qiáng)度準(zhǔn)則

可以借助摩爾圓來(lái)討論硐室圍巖的強(qiáng)度，如圖4所示。摩爾圓的包絡(luò)關(guān)系可以由下式表達(dá)：

在開(kāi)始使用在線社交應(yīng)用時(shí)，用戶(hù)需要先向在線社交應(yīng)用提交自己的隱私需求，即，對(duì)不同類(lèi)型的請(qǐng)求者，他們最后看到的隱私信息的詳細(xì)程度。這些不同的需求以隱私規(guī)則的方式存儲(chǔ)在數(shù)據(jù)庫(kù)中，由在線社交應(yīng)用進(jìn)行管理。用戶(hù)只要定義好自己的隱私需求，在以后的使用過(guò)程中系統(tǒng)會(huì)將他的需求應(yīng)用到他所有發(fā)布的消息中，不需要用戶(hù)自身來(lái)管理各種權(quán)限的請(qǐng)求者可以得到什么樣的內(nèi)容，簡(jiǎn)化了用戶(hù)的工作。

圖4 硐室開(kāi)挖前后側(cè)墻圍巖應(yīng)力圓[1]Fig.4 The stress circles of surround rocks before and after the tunneling

式中：σn=(σr+σθ)/2。

眾所周知，式(10)所示的強(qiáng)度準(zhǔn)則由內(nèi)摩擦角和內(nèi)聚力兩個(gè)特征強(qiáng)度參數(shù)來(lái)近似描述，它反映了圍巖加載直至斷裂的力學(xué)行為，但只涉及第一、三主應(yīng)力，這意味著在構(gòu)建摩爾圓包絡(luò)關(guān)系時(shí)不考慮最大摩爾圓之外的其他摩爾圓。目前有眾多的表達(dá)式來(lái)表示τ 與σn之間的關(guān)系[33]，但是有兩個(gè)問(wèn)題需要強(qiáng)調(diào)：第一個(gè)問(wèn)題是，在這些關(guān)系式中σz不影響強(qiáng)度的von Karman 關(guān)系：即在最大摩爾圓達(dá)到極限時(shí)，不會(huì)破壞第二主方向上應(yīng)力與應(yīng)變的彈性關(guān)系；第二個(gè)問(wèn)題是，這些關(guān)系式表達(dá)的脆性破壞強(qiáng)度準(zhǔn)則不依賴(lài)于σz，材料彈性地達(dá)到斷裂點(diǎn)[34-35]，很多巖石的變形和強(qiáng)度數(shù)學(xué)模型都是如此。

2.1.2三維強(qiáng)度準(zhǔn)則

在復(fù)雜應(yīng)力條件下，僅考慮第一主應(yīng)力σθ與第三主應(yīng)力σr所得到的巖石強(qiáng)度與實(shí)際有較大偏差，為此Shemyakin[36-37]通過(guò)引入Lode 參數(shù)μσ來(lái)研究第二主應(yīng)力σz對(duì)強(qiáng)度的影響，他提出的三維強(qiáng)度準(zhǔn)則為：

式中：τ1=(σz?σr)/2，τ2=(σθ?σz)/2。

式(11)所表示的是一個(gè)強(qiáng)度曲面，當(dāng)μσ取不同值時(shí)即為不同應(yīng)力狀態(tài)下的強(qiáng)度曲線（見(jiàn)圖5）。其中μσ影響的力學(xué)意義在于：在復(fù)雜應(yīng)力狀態(tài)下（μσ≠0），材料的強(qiáng)度不僅由最大剪切力決定，同時(shí)也由τ1和τ2決定，即不同類(lèi)型壓力狀態(tài)導(dǎo)致不同的變形過(guò)程。

圖5 三向應(yīng)力狀態(tài)時(shí)的強(qiáng)度準(zhǔn)則Fig.5 Strength criterion at triaxial stress state

為了得到式(11)的函數(shù)曲面，必須進(jìn)行三軸加載實(shí)驗(yàn)。圖6為根據(jù)式(11)對(duì)文獻(xiàn)[20]中錦屏大理巖真三軸實(shí)驗(yàn)數(shù)據(jù)進(jìn)行整理的結(jié)果，巖石試樣取自深約2.4 km 的錦屏二期地下實(shí)驗(yàn)室。圖6（a）顯示，隨著 μσ的增大，不同圍壓時(shí)大理巖強(qiáng)度均有不同程度的增大。通過(guò)設(shè)定不同的應(yīng)力狀態(tài)（μσ）進(jìn)行真三軸加載實(shí)驗(yàn)，可獲得一系列強(qiáng)度包絡(luò)線族，如圖6（b）所示，進(jìn)而得到式(11)所表示的強(qiáng)度空間曲面。

圖6 錦屏大理巖真三軸實(shí)驗(yàn)結(jié)果Fig.6 The true triaxial test results of themarble in Jinping.

2.1.3深部圍巖峰后長(zhǎng)期變形特性

如上所述，深部硐室圍巖的強(qiáng)度不僅由最大剪切力決定，同時(shí)也由τ1和τ2決定。即在復(fù)雜應(yīng)力狀態(tài)下（μσ≠0），Lode參數(shù) μσ不僅在評(píng)估原始應(yīng)力狀態(tài)時(shí)應(yīng)當(dāng)考慮，在深部硐室工作面掘進(jìn)的方向上也應(yīng)當(dāng)考慮。

在評(píng)價(jià)深部硐室長(zhǎng)期穩(wěn)定性中，也必須考慮切向力τ、τ1和τ2在直至破裂點(diǎn)的變形過(guò)程中的作用，如圖7中應(yīng)力應(yīng)變曲線τ=τ(γ)所展示的那樣，圍巖在剪切應(yīng)變?yōu)棣胑時(shí)達(dá)到剪切強(qiáng)度，而直至為γ0時(shí)才發(fā)生宏觀破碎，圖中γ=εr?εθ為主剪應(yīng)變，εV=εr+εθ為體積應(yīng)變。因此用應(yīng)力達(dá)到極限應(yīng)力狀態(tài)來(lái)判斷圍巖達(dá)到強(qiáng)度極限或認(rèn)為圍巖喪失承載能力是不充分的，必須考慮圍巖峰后的變形特性，包括不可逆剪切變形、體積擴(kuò)容（剪切或拉伸），以及在不可逆變形區(qū)域的裂縫極限寬度。

圖7 體積變形與剪切變形的關(guān)系Fig.7 The relationship between bulk and shear deformations

深部硐室圍巖的峰后變形行為均伴隨著塊體間的互相轉(zhuǎn)動(dòng)與滑動(dòng)等各向異性特點(diǎn)，滑移面上的法向應(yīng)力（以及由此產(chǎn)生的摩擦力）和變形的時(shí)間效應(yīng)（巖石中的蠕變和松弛）決定著不可逆變形與破壞的形態(tài)（剪切、劈裂）。體積的改變則與膨脹及破壞所形成的塊體的大小有關(guān)，這種體積變化的效應(yīng)正是深部硐室圍巖穩(wěn)定性控制最本質(zhì)的問(wèn)題。

2.2 深部硐室圍巖長(zhǎng)期變形機(jī)理

2.2.1地下硐室長(zhǎng)期變形計(jì)算的一般公式

在研究圍巖的變形與破壞（剪脹與劈裂擴(kuò)容）過(guò)程中，可利用質(zhì)量守恒定律計(jì)算硐室圍巖不可逆變形區(qū)（塑性區(qū)）內(nèi)介質(zhì)的位移[38]。

圖8為塑性區(qū)的位移示意圖，ur為半徑r處巖體的位移，uc為不可逆變形區(qū)邊界處的位移，從半徑r至塑性區(qū)邊界c處的巖體在發(fā)生位移前后質(zhì)量不變，取軸向長(zhǎng)度為單位長(zhǎng)度，則有：

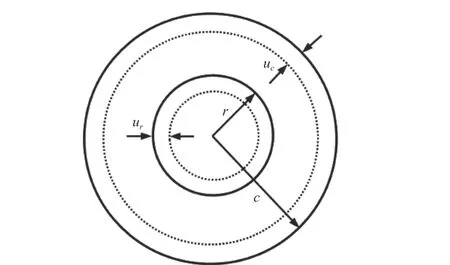
圖8 塑性區(qū)圍巖位移示意圖Fig.8 The deformation of surrounding rocks in the plastic zone

式中：ρ0與ρ′分別為位移前后巖體的密度。根據(jù)式(12)可進(jìn)一步求得塑性區(qū)內(nèi)半徑為r處巖體的位移：

彈塑性邊界的位移uc可由r=c處的連續(xù)條件得到[36]：

式中：ξ?根據(jù)圍巖分區(qū)邊界條件而定，對(duì)于圍巖彈塑性邊界，ξ?=γe(1?ν)，ν為介質(zhì)的泊松比，γe為圍巖的彈性極限剪應(yīng)變，ξ?為無(wú)物理意義的記號(hào)。考慮到ρ0/ρ′=1+?V/V0=1+εV，εV為體積擴(kuò)容應(yīng)變（包括剪切變形導(dǎo)致的擴(kuò)容以及劈裂帶來(lái)的擴(kuò)容），將其代入式(13)可得塑性區(qū)位移為：

半徑為a的硐室邊壁上的位移為：

上述依據(jù)質(zhì)量守恒得到的表達(dá)式(17)對(duì)圍巖的變形計(jì)算來(lái)講可看作是一般形式。式(17)清楚地表明，圍巖總的位移由第一項(xiàng)剪切變形和第二項(xiàng)擴(kuò)容變形構(gòu)成。

2.2.2深部硐室圍巖長(zhǎng)期變形機(jī)理

塑性區(qū)圍巖變形由剪切變形和擴(kuò)容變形構(gòu)成，它們形成位移的機(jī)理不同，在總位移中所占比重也不同。對(duì)于剪切變形，選用Tresca 屈服準(zhǔn)則，由經(jīng)典彈塑性理論可知：當(dāng)σ0≥τmax時(shí)，硐室圍巖進(jìn)入到塑性狀態(tài)。要確定圍巖的剪切變形破壞條件，如前所述（見(jiàn)圖7），需引入τ=τ(γ)峰后變形曲線有關(guān)的參量。對(duì)于理想脆性材料，剪應(yīng)力峰值對(duì)應(yīng)的剪切應(yīng)變?yōu)棣胑=γ0，其中γ0為破壞極限剪應(yīng)變；但對(duì)于允許不可逆變形的巖石而言，γ0可超過(guò)γe一個(gè)數(shù)量級(jí)以上。該模型反映了真實(shí)巖體的重要性質(zhì)，即存在巖體不可逆變形的臨界應(yīng)變?chǔ)胑以及巖體破碎的應(yīng)變?chǔ)?。圍巖在進(jìn)入塑性狀態(tài)以后將繼續(xù)承載，同時(shí)產(chǎn)生較大的剪切變形。當(dāng)圍巖內(nèi)壁應(yīng)變達(dá)到γ0時(shí)，出現(xiàn)破碎。圍巖因剪切破壞可能會(huì)導(dǎo)致單元體積變化，即剪脹效應(yīng)。為了評(píng)估剪切導(dǎo)致的體積變化，按照上述模型選取最大的剪切變形值γ0，則體積變化 εV與破壞應(yīng)變?chǔ)?的關(guān)系可以近似取為線性關(guān)系[39]：

式中：Λ為擴(kuò)容系數(shù)，0≤Λ≤1，可用特殊實(shí)驗(yàn)設(shè)備測(cè)得擴(kuò)容體積的變化。由于剪切破壞應(yīng)變?chǔ)?是個(gè)常量，因而產(chǎn)生的體積變化一般不大。

深部硐室圍巖體積變化的第二個(gè)原因是圍巖可能發(fā)生“劈裂擴(kuò)容”，即出現(xiàn)有平行于最大壓應(yīng)力的裂縫區(qū)或者是被裂縫區(qū)分離開(kāi)的柱狀構(gòu)造[40-41]（見(jiàn)圖9）。在各向不均勻壓縮條件下，材料可能被破壞面分割（劈裂），其方向沿著最大壓應(yīng)力的方向。在本文所研究的問(wèn)題中，最大壓應(yīng)力就是圍巖中的環(huán)向應(yīng)力σθ。在壓應(yīng)力 σθ作用下，即使另外兩個(gè)方向存在壓縮（約束）應(yīng)力 σr和 σz，沿著σr方向也會(huì)形成拉伸變形，這些變形可以達(dá)到裂縫極限寬度（見(jiàn)圖10）。

圖9 地下硐室圍巖劈裂示意圖[1]Fig.9 The schematic diagram of spalling of rocks surrounding deep level tunnels[1]

圖10 深部圍巖劈裂示意圖Fig.10 The splitting of deep surrounding rocks

當(dāng)出現(xiàn)劈裂區(qū)時(shí)，圍巖產(chǎn)生的位移可分解成兩部分：一部分是直接在硐室附近區(qū)域中由巖體剪切變形產(chǎn)生的位移；第二部分是在圍巖深處支撐壓力區(qū)出現(xiàn)“虛假”隧道輪廓面而產(chǎn)生的位移（此部分位移主要來(lái)源于劈裂區(qū)圍巖的體積擴(kuò)容），如圖11所示。這類(lèi)“虛假”隧道輪廓面區(qū)域可能有幾個(gè)，它取決于隧道所處位置的巖石壓力和峰后變形狀態(tài)下材料的剩余強(qiáng)度。需要指出的是，上述兩部分位移均包含于質(zhì)量守恒方程中，如式(17)所示。后面將給出上述兩部位移的具體計(jì)算過(guò)程。

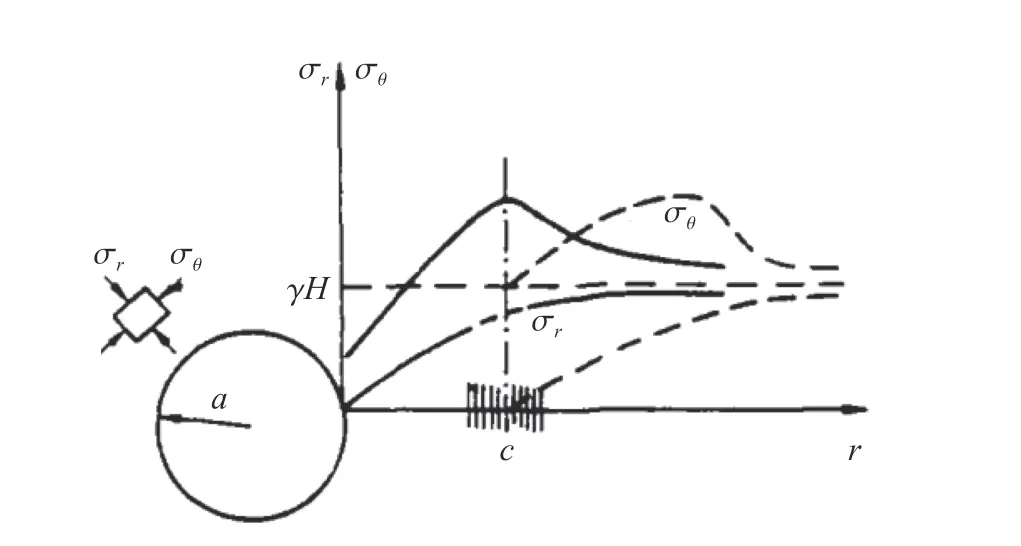
圖11 深部圍巖分區(qū)破裂示意圖Fig.11 Diagram of zonal disintegration of deep surrounding rocks

深部硐室圍巖分區(qū)破裂的發(fā)生條件仍是個(gè)懸而未決的問(wèn)題，關(guān)于其在圍巖什么位置發(fā)生需要回答兩個(gè)問(wèn)題：

第一個(gè)問(wèn)題是在多大臨界初始地應(yīng)力下可能出現(xiàn)劈裂破壞？

第二個(gè)問(wèn)題是大于臨界初始地應(yīng)力條件下，分區(qū)破裂的空間構(gòu)造如何？

2.2.3深部硐室圍巖劈裂破壞機(jī)制與條件

假設(shè)卸荷后應(yīng)力調(diào)整的時(shí)間為tmax，根據(jù)經(jīng)典彈性理論可知彈塑性邊界處環(huán)向應(yīng)力σθ的變化量為+τmax，徑向應(yīng)力σr的變化量為?τmax，軸向應(yīng)力不變。假定應(yīng)力變化過(guò)程為線性過(guò)程，那么應(yīng)力轉(zhuǎn)移過(guò)程中t時(shí)刻的應(yīng)力（應(yīng)力以壓為正）為：

按平面應(yīng)變計(jì)算，應(yīng)用廣義胡克定律可得應(yīng)變?yōu)椋?/p>

式中：Ee為巖石楊氏模量（卸載模量）。

缺陷處應(yīng)力集中的演化方程為Maxwell 形式[29]：

式中：Ec為缺陷附近的壓縮模量，為方便表征和測(cè)量可近似為巖石的塑性加載模量，? σr為裂隙附近σr方向的附加應(yīng)力，J為特定尺寸缺陷上的應(yīng)力集中系數(shù)，l為缺陷尺寸，η為附加應(yīng)力的松弛速率，er為偏應(yīng)變，er=εr?(εr+εθ+εz)/3，由式(21)可得：

將式(23)對(duì)t求導(dǎo)，并將導(dǎo)數(shù)代入式(22)可得：

根據(jù)初始條件t=0時(shí)?σr=0，解式(24)關(guān)于? σr的微分方程可得：

一般情況下，η的量級(jí)為10?8m/s，同時(shí)圍巖在開(kāi)挖后因彈性回彈誘發(fā)松動(dòng)而存在較大尺寸的缺陷，因此滿(mǎn)足l＞＞ ηt，因而式(25)可以進(jìn)一步簡(jiǎn)化為：

式(26)表明在徑向方向存在拉伸的附加應(yīng)力。這就回答了有關(guān)封閉應(yīng)力重要特點(diǎn)的第一個(gè)問(wèn)題，即圍巖在卸載后可能出現(xiàn)拉應(yīng)力。

將式(26)代入式(19)可得單元體內(nèi)徑向局部應(yīng)力為：

式(28)回答了在多大臨界初始地應(yīng)力下可能出現(xiàn)劈裂破壞的問(wèn)題。一般各向異性巖石的楊氏模量Ee大于加載模量Ec，因此根據(jù)式(26)求得的附加應(yīng)力大小要大于各向同性(Ee=Ec)情況下的附加應(yīng)力，即不均勻各向異性巖石較之均勻各向同性巖石更容易發(fā)生劈裂破壞。

Shemyakin[37]基于彈塑性理論給出了深部硐室圍巖剪切破壞峰后的破碎條件。這就是為什么進(jìn)入深部的硐室圍巖一般更容易出現(xiàn)劈裂破壞或分區(qū)破裂現(xiàn)象的原因，該問(wèn)題在實(shí)際深部工程中研究得還很少，需給予重視。

文獻(xiàn)[25]初步回答了第二個(gè)問(wèn)題（分區(qū)破裂的空間構(gòu)造），給出的分區(qū)破裂半徑為：

式中：ci為第i破裂區(qū)半徑，i=1,2,3,···代表出現(xiàn)分區(qū)破裂的圈數(shù)。從能量釋放的角度一般不會(huì)超過(guò)4圈（不包括硐室邊壁出現(xiàn)小的劈裂區(qū)）。

引入圍巖無(wú)量綱能量因子：

式中：Wp為開(kāi)挖后圍巖塑性區(qū)內(nèi)應(yīng)力釋放的能量，M為塑性區(qū)巖體質(zhì)量，cP為巖體縱波波速。k作為無(wú)量綱參數(shù)可以表征巖體的能量狀態(tài)。

依據(jù)式(32)得到分區(qū)破裂半徑ci/a與能量因子k之間的關(guān)系[25]（見(jiàn)圖12和表1），可見(jiàn)隨塑性區(qū)發(fā)展能量因子具有穩(wěn)定的等級(jí)遞減規(guī)律，直至塑性區(qū)圍巖能量因子為1.4×10?9。

圖12 分區(qū)破裂半徑計(jì)算與監(jiān)測(cè)結(jié)果對(duì)比[25]Fig.12 A comparison between the in-situ and theoretical radiiof zonal disintegration[25]

表1 分區(qū)破裂區(qū)半徑ci/a 與能量因子k 之間的關(guān)系[25]Table 1 The relationship between the radii of zonal disintegration ci/a and theenergy factor k[25]

2.3 深部硐室圍巖劈裂破壞不可逆位移

根據(jù)深部硐室圍巖大量現(xiàn)場(chǎng)破壞現(xiàn)象，如圖9（A 或B）所示，可以認(rèn)為硐室附近出現(xiàn)劈裂破壞是由垂直或平行裂縫群構(gòu)成。設(shè)每個(gè)裂縫寬度為δ，其占有的鄰近巖塊尺度為L(zhǎng)，變形主要由裂隙開(kāi)裂寬度構(gòu)成，如果引入巖體等級(jí)構(gòu)造的關(guān)系式δ=ψ?L[9],其中巖石力學(xué)不變量為ψ?=(0.5 ～2)×10?2，那么硐室圍巖的擴(kuò)容體積變形為：

劈裂擴(kuò)容與剪切滑移在邊壁產(chǎn)生的位移依據(jù)式(17)可得:

將式(32)代入式(35)可得:

根據(jù)式(36)可以估算深部硐室在沒(méi)有支護(hù)或支護(hù)能力不足的情況下，經(jīng)過(guò)長(zhǎng)時(shí)間圍巖出現(xiàn)破裂的變形值。采用文獻(xiàn)[17-18,43]提供的錦屏一級(jí)水電站地下廠房的基本參數(shù)與多點(diǎn)檢測(cè)數(shù)據(jù)進(jìn)行比較。

基本參數(shù)為：主變室跨度19.3 m，高32.7 m，等效圓形半徑14.17 m；主廠房跨度25.9 m，高68.8 m，等效圓形半徑為23.82 m；兩個(gè)尾調(diào)室側(cè)壁為豎直圓柱狀，最大位移發(fā)生在半徑較小的2號(hào)尾調(diào)室，半徑為17.5 m。初始應(yīng)力σ0=20～35.7 MPa，圍巖為大理石，其基本參數(shù)為：τmax=15.5 MPa ，γe=1.275×10?3，ν=0.25，ξ?=γe(1?ν)=0.96×10?3。

（1）現(xiàn)場(chǎng)監(jiān)測(cè)數(shù)據(jù)：現(xiàn)場(chǎng)初始地應(yīng)力與剪切強(qiáng)度比為σ0/τmax=1.3 ～2.3，滿(mǎn)足式(28)劈裂條件。主變室出現(xiàn)第一圈破裂區(qū)距邊壁為8～9 m，且在深8 m 范圍內(nèi)圍巖發(fā)生了劈裂，邊壁局部變形達(dá)23.3 cm；主廠房第一圈破裂區(qū)距邊壁13 cm，邊壁位移最大為上游側(cè)22 cm，下游側(cè)24.7 cm；尾調(diào)室圍巖未發(fā)生明顯的劈裂破壞，邊壁局部位移最大達(dá)12.5 cm。

（2）劈裂發(fā)生位置理論與實(shí)測(cè)對(duì)比驗(yàn)算：主變室第一圈破裂區(qū)半徑與等效開(kāi)挖半徑之比c/a=1.64，與式(32)理論預(yù)測(cè)的第一圈exp(1/2)≈1.65相當(dāng)吻合。主廠房c/a=1.55，與式(32)理論預(yù)測(cè)的第一圈exp(1/2)≈1.65基本吻合。誤差主要來(lái)源于等效半徑，主廠房高垮比為2.67，而主變室僅為1.7。

（3）側(cè)壁位移理論與實(shí)測(cè)對(duì)比驗(yàn)算：側(cè)壁局部位移變化是隨時(shí)間而積累的過(guò)程，可以通過(guò)對(duì)ψ?在其范圍內(nèi)取不同的值加以表征。根據(jù)式(36)分別得到劈裂擴(kuò)容與剪切變形值，計(jì)算結(jié)果列入表2，可見(jiàn)實(shí)測(cè)的數(shù)值均在理論最大變形之內(nèi)。其中尾調(diào)室尚未發(fā)生明顯的分區(qū)破裂，因此變形還在發(fā)展的初級(jí)階段，也與實(shí)際相符。

表2 圍巖變形理論與現(xiàn)場(chǎng)實(shí)測(cè)結(jié)果對(duì)比Table 2 Comparison of the theoretical and in-situ results

根據(jù)式(36)計(jì)算的硐室圍巖變形為開(kāi)挖后無(wú)支護(hù)條件下的自然位移，而支護(hù)的存在會(huì)減緩變形的發(fā)展，因此實(shí)際位移都尚未達(dá)到模型預(yù)測(cè)的最終值。從表中也可以看出，圍巖的變形主要為劈裂擴(kuò)容變形，剪切的貢獻(xiàn)較小，相差可達(dá)一個(gè)數(shù)量級(jí)。

根據(jù)深部硐室圍巖的分區(qū)破裂范圍，就可以確定錨桿長(zhǎng)度，以滿(mǎn)足圍巖長(zhǎng)期穩(wěn)定而不開(kāi)裂的條件；而根據(jù)圍巖的變形量可以確定錨桿的強(qiáng)度，使其受力在正常工作區(qū)間內(nèi)而不斷裂。

3 結(jié) 論

（1）巖體固有的非均勻性與封閉應(yīng)力特征，是決定深部硐室圍巖長(zhǎng)期變形與地震穩(wěn)定性的最本質(zhì)的因素。隨著埋深增加，硐室圍巖非均勻變形必將形成塊系構(gòu)造單元非協(xié)調(diào)變形，而圍巖中封閉應(yīng)力不僅影響其塊系構(gòu)造單元局部動(dòng)力穩(wěn)定性，也影響其長(zhǎng)期變形破壞形態(tài)。

（2）深部硐室圍巖的破壞準(zhǔn)則不僅要考慮巖體三維強(qiáng)度準(zhǔn)則，也要考慮圍巖峰后變形及斷裂準(zhǔn)則。

（3）深部硐室圍巖長(zhǎng)期變形計(jì)算服從質(zhì)量守恒定律，深部圍巖出現(xiàn)劈裂的條件表明，圍巖長(zhǎng)期變形過(guò)程中更容易出現(xiàn)劈裂破壞導(dǎo)致的分區(qū)破裂化擴(kuò)容效應(yīng)，這種擴(kuò)容變形比剪切不可逆變形高一個(gè)數(shù)量級(jí)。

（4）根據(jù)深部硐室圍巖的分區(qū)破裂范圍，可以確定錨桿長(zhǎng)度，以滿(mǎn)足長(zhǎng)期穩(wěn)定而不開(kāi)裂的條件；根據(jù)圍巖最大變形量，可以確定錨桿的強(qiáng)度，使其受力在正常工作區(qū)間內(nèi)而不斷裂。對(duì)于支護(hù)的變形位移計(jì)算理論將在后續(xù)研究中完成。

感謝梁文灝院士、馮夏庭院士提出的寶貴修改意見(jiàn)。