基于Ransac算法的捷變頻聯合正交頻分復用雷達高速多目標參數估計

全英匯 高 霞* 沙明輝 方 文 李亞超 邢孟道

①(西安電子科技大學電子工程學院 西安 710071)

②(北京無線電測量研究所 北京 100854)

③(西安電子科技大學雷達信號處理國家重點實驗室 西安 710071)

1 引言

隨著現代電子技術的迅速發展，電磁環境日益復雜，雷達面臨的威脅不斷增多，目標檢測和參數估計的能力受到嚴重影響。為了提高綜合作戰性能，許多新體制雷達應運而生[1,2]。而廣泛應用于通信領域的正交頻分復用(Orthogonal Frequency Division Multiplexing, OFDM)技術也被引入到雷達系統中，其易于實現頻譜資源控制和無線環境下的高速傳輸的優勢，吸引了大批學者的關注[3,4]。在雷達中，利用OFDM信號的大時寬帶寬積特性進行脈沖壓縮等處理，可以獲得目標的距離和多普勒信息，因此，OFDM信號具備了雷達網間通信與目標探測的雙重優勢[5]。文獻[6]將OFDM信號運用于多輸入多輸出(Multiple Input Multiple Output,MIMO)雷達，研究了雷達通信一體化信號的共享設計。文獻[7,8]在步進頻雷達中采用了OFDM技術，采用離散傅里葉變換(Discrete Fourier Transform,DFT)技術合成目標的距離-速度2維像，但是該方法的前提是目標個數少并且速度相似，當觀測場景內存在多個速度相差很大的目標時，這一方法不再適用。文獻[9]提出了兩種捷變頻聯合正交頻分復用(Frequency Agility-OFDM, FA-OFDM)雷達信號形式，并且分析了兩種信號的模糊函數，為FA-OFDM雷達的回波信號處理提供了思路。然而，對于FAOFDM雷達而言，發射信號的頻率隨機跳變導致回波相位不連續，使得雷達難以對目標進行檢測，其目標參數估計仍是一個亟待解決的問題。文獻[10]提出了步進頻OFDM雷達實現距離高分辨的方法，但是該方法對速度敏感，只適用于低速目標。文獻[8]針對步進頻OFDM雷達多目標參數估計問題，提出了一種改進的DFT信號處理方法，該方法以較低的A/D采樣率在不增加計算量的同時獲取目標距離-速度信息。文獻[11]針對FA-OFDM雷達通過合成不同載波的多個窄帶信號來實現距離高分辨，但是該方法只適用于靜止或低速目標。文獻[8]研究了頻率捷變稀疏OFDM雷達目標參數估計的問題，通過對多個窄帶子載波采用壓縮感知技術處理，等效合成大帶寬，獲取目標高分辨距離-速度信息，但該方法只對低速目標進行了研究。文獻[12]針對OFDM雷達，提出了一種基于通道分離和最大似然原理相結合的運動參數估計方法，利用Keystone變換CLEAN技術對距離-多普勒2維譜進行譜峰搜索，獲得各個目標的位置和速度參數估計量，但該方法采用牛頓迭代算法對似然函數進行優化，運算量過大。基于此，文獻[13]提出了一種基于期望最大化算法的捷變頻聯合正交頻分復用雷達高速多目標參數估計的方法，但是該方法只適用于信噪比較高的情況，當有大量噪聲存在時該方法幾乎完全失效。針對上述問題，本文提出一種基于隨機抽樣一致算法(Random sample consensus, Ransac)的FA-OFDM雷達高速多目標參數估計的方法。本方法不僅能夠獲得目標的高分辨距離信息，還可以在低信噪比情況下有效地對高速多目標的速度進行同時估計。

2 FA-OFDM雷達信號模型

OFDM雷達發射波形設計靈活，理論上可以進行任何形式的調制，最常見的有線性調頻調制(Linear Frequency Modulation, LFM)和相位編碼(Phase Coded, PC)調制。本文采用LFM調制，發射信號示意圖如圖1所示。FA-OFDM雷達發射脈間載頻捷變的信號，并且每個脈沖寬度內同時發射多個頻率隨機跳變的子載波，從而獲得大的時寬帶寬積，提高雷達分辨率，同時使得雷達能有效地規避窄帶瞄準式干擾。

圖1中，Tp表示脈沖寬度，Tr表示脈沖重復周期。FA-OFDM雷達的發射信號可以寫為

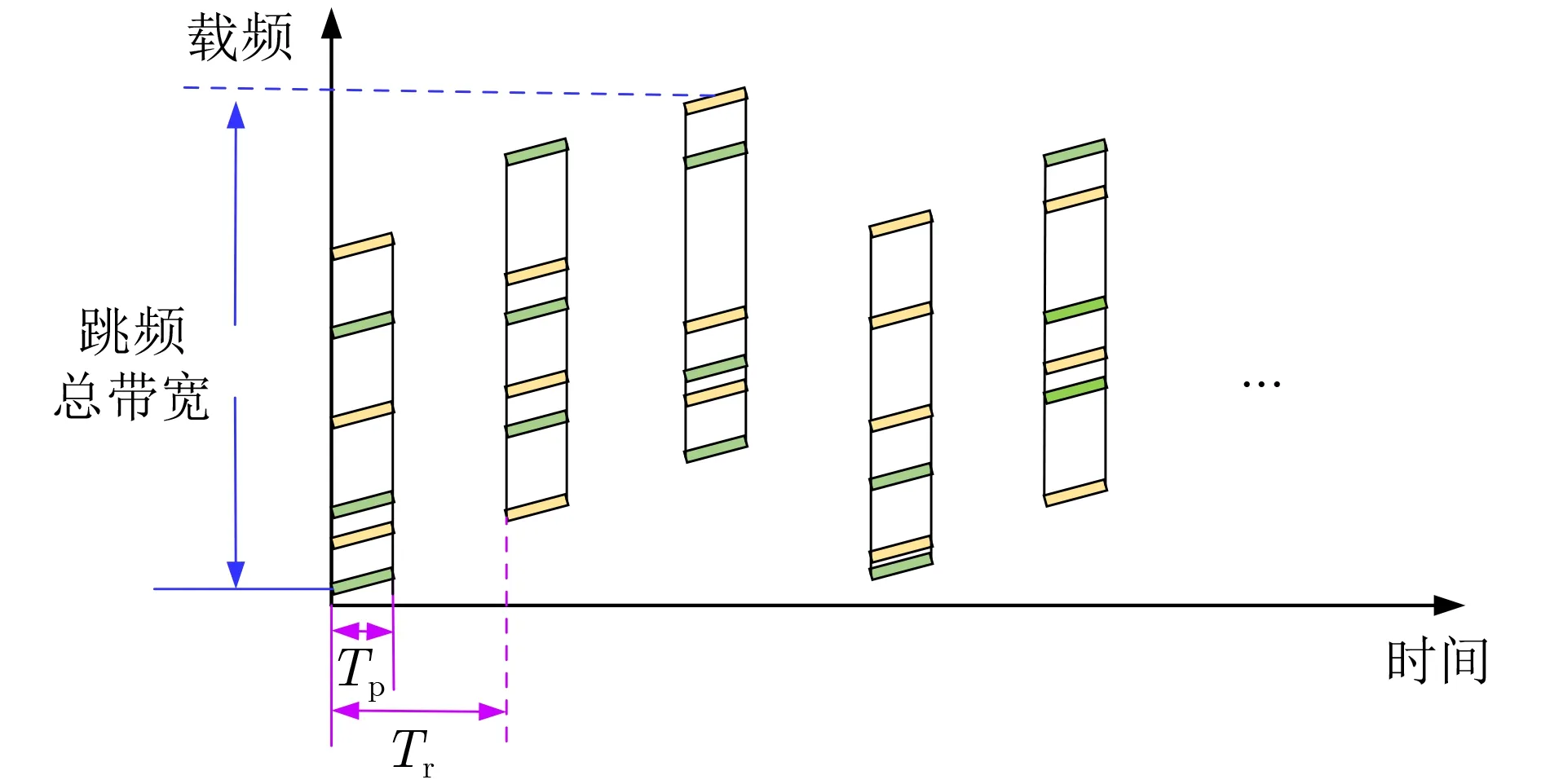
圖1 FA-OFDM雷達發射信號示意圖

3 基于IAA的目標高分辨距離合成方法

正如文獻[13]所述，由于載頻捷變導致回波信號的多普勒相位不連續，許多學者采用基于壓縮感知(Compress Sensing, CS)的方法實現目標稀疏重構[14,15]。而FA-OFDM信號是在1個脈沖寬度內同時發射多個頻率捷變的子載波。因此，對單個脈沖的所有子載波回波信號先進行脈沖壓縮，再通過CS實現稀疏重構，即可得到目標在該時刻的高分辨距離信息[13]。本文采用迭代自適應譜估計(Iterative Adaptive Approach, IAA)方法代替基于CS的稀疏重構方法來合成目標的高分辨距離[16]。

對第n個脈沖的回波而言，匹配濾波輸出為

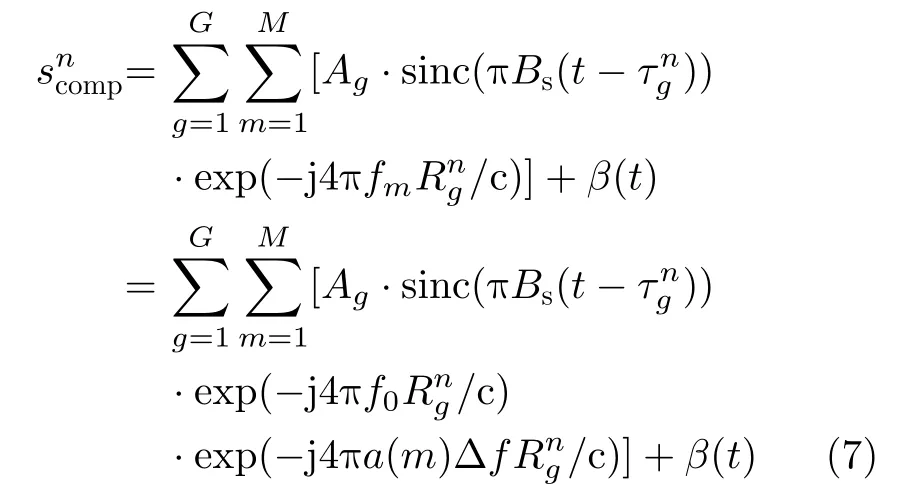
與基于CS的稀疏重構方法類似，當目標場景滿足稀疏性時，IAA算法也可以用于目標的距離維譜估計。該算法是由Jensen等人在2009年提出的[17–19]，它的基本思想是通過循環迭代，利用上一次迭代的譜估計結果構建信號協方差矩陣，并將其逆陣作為加權矩陣代入加權最小二乘中求解。

優化問題式(9)的解為

其中

表示細分辨距離單元，δ(·)為單位沖激函數。

假設3個相鄰目標位于第290個粗分辨單元，細分辨距離單元的索引分別為[4, 13, 20]。FA-OFDM雷達系統在單個脈沖寬度內同時發射多個頻率捷變的子載波，合成大帶寬，提高了距離分辨率。對第1個脈沖中所有子載波的回波進行匹配濾波的輸出如圖2(a)所示，可以看出結果中只有1個峰值，無法正確檢測目標個數。而采用IAA方法合成目標高分辨距離的結果如圖2(b)所示，3個相鄰目標可以被準確區分。

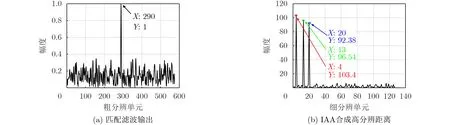
圖2 3個相鄰目標仿真結果圖

4 基于Ransac算法的高速多目標速度估計

如第2節和第3節所述方法，通過對不同脈沖時刻的回波進行匹配濾波和迭代自適應譜估計，得到多個目標在不同時刻的距離高分辨信息。根據目標的時刻-距離直線的斜率來估計目標的速度。當觀測場景中只存在單個目標時，可以采用最小二乘法來擬合直線，但當存在多個目標時，最小二乘法不再適用。文獻[13]提出了基于EM算法的多目標速度估計方法，這一方法雖然可以對高速運動的多目標進行有效的速度估計，但是對目標回波的信噪比要求比較高，當信噪比低于一定值時，譜估計的結果中出現很多無效的噪聲點，它們會嚴重影響EM算法的性能，甚至可能導致直線擬合失敗。為了解決這一問題，本文提出了一種基于Ransac算法的高速多目標速度估計方法。

4.1 Ransac算法

隨機抽樣一致算法(Ransac)，最早是由Fischler和Bolles提出用于解決位置確定問題(Location Determination Problem, LDP)的。Ransac算法采用迭代的方式從一組包含離群的觀測數據中估算出數學模型的參數，廣泛應用于直線擬合、平面擬合等方面[20,21]。數據中包含正確數據記為“內點”和異常數據(或稱為噪聲)記為“外點”。Ransac算法是一種不確定算法，它只能在一定概率下產生結果，并且這個概率會隨著迭代次數的增加而提高。

設內點在數據中所占的比例為ρ，迭代次數為i，則采用Ransac算法得到正確模型的概率為

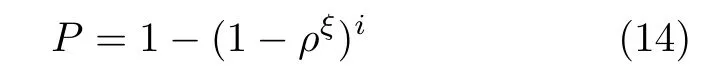
ξ為求解模型所需的最小數據點數。通過式(14)可以求得

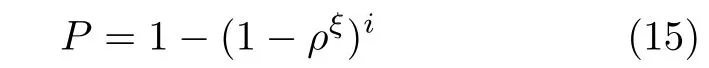
4.2 基于Ransac算法的參數估計

本節針對多個目標的數據點構造多個直線模型，基于Ransac算法的直線擬合的步驟如下：

(1) 輸入各采樣時刻及其對應的高分辨距離，稱為觀測數據集；

根據式(12)可以得到Y個觀測數據(ty,{Ry})。{Ry}表示ty時刻多個目標經過稀疏重構得到的高分辨距離，由于噪聲點(外點)的存在，{Ry}是一個長度不確定的集合。實際觀測數據的個數(內點個數+外點個數)通常會大于理論觀測數據的個數(內點個數)，滿足Y ≥G×N。

(2) 輸入要擬合的直線數目(即目標個數)G；

(3) 針對每條直線，確定適用于模型的最小數據個數為2，兩點確定一條直線；

從觀測數據集中隨機選取2個點，構造直線模型，記為最優直線Rbest。第g個目標的直線模型可以表示為

綜上，本文所提算法的信號處理流程圖如圖3所示。

圖3 基于Ransac算法的高速多目標參數估計方法的流程圖

5 仿真結果及分析

5.1 仿真結果

為了驗證所提算法的有效性，本節分別對文獻[13]和所提算法進行了仿真與分析。FA-OFDM雷達的發射信號如圖1所示，實驗參數如表1所示。

高信噪比情況：取輸入信噪比為–12 dB。如表1所示，在FA-OFDM雷達中1個CPI內有64個脈沖，每個脈沖寬度內發射64個頻率隨機跳變的子載波，合成大帶寬，距離分辨率得以提高。遠場觀測場景內存在3個不同距離、不同速度的目標，經過目標散射后，雷達回波信號中包含了目標的時延和多普勒信息。首先對單個脈沖內的所有子載波回波信號進行脈沖壓縮獲得粗分辨距離信息，如圖4(a)所示，再通過IAA方法合成高分辨距離，結果如圖4(b)所示。根據峰值所在的位置計算出3個目標的距離分別為[3993.9, 4002.4, 4005.7] m，與真實距離的誤差均小于0.1%。進一步地，分別對64個脈沖回波采用IAA方法合成目標高分辨距離，得到時間-距離圖，如圖4(c)所示。將各個脈沖時刻及其對應的高分辨距離信息構成觀測數據集，按照4.2節所述步驟，采用Ransac算法同時擬合多條直線，結果如圖4(e)所示。而按照文獻[13]中所提的EM算法進行直線擬合的結果如圖4(d)所示。對比圖4(d)和圖4(e)，可以看出兩種方法均可同時擬合3條直線，由此估計的目標速度誤差均小于0.9%，當信噪比為–12 dB時，兩種算法都可以有效地對多目標的速度進行估計。

表1 仿真參數

低信噪比情況：取輸入信噪比為–28 dB。與圖4對比，圖5(a)為3個目標的時間-距離圖，可以看出當輸入信噪比過低時，有大量噪聲點出現，這會嚴重影響直線擬合的性能。作者在文獻[13]中所提EM算法的直線擬合結果如圖5(b)所示，盡管擬合出了3條直線，但其斜率對應的速度與真實目標速度相差甚遠，無法對目標進行正確的參數估計，文獻[13]所提算法幾乎完全失效。而采用本文所提Ransac算法進行直線擬合的結果如圖5(c)所示，可以看到3條直線被成功擬合，其直線斜率對應的速度分別為[614.19, 1195.79, 5918.56] m/s，相對誤差分別為2.37%, 1.98%, 2.04%。在一定誤差允許范圍內，本文所提算法可以有效地同時對多目標的速度進行準確估計。

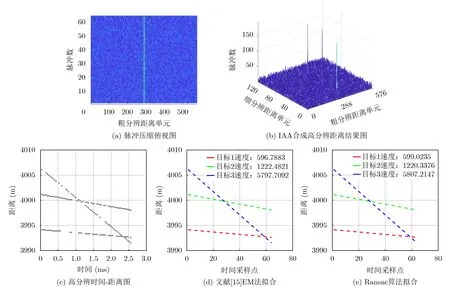
圖4 信噪比為–12 dB時的仿真結果

圖5 信噪比為–28 dB時的仿真結果

5.2 性能分析

為了進一步研究所提算法在不同條件下的性能，本節參照文獻[13]分析了不同輸入信噪比(接收回波的信噪比)情況下的檢測概率以及同速度條件下的估計誤差。

首先，研究了輸入信噪比在–32～20 dB(對應輸出信噪比為–4～8 dB)[13]范圍內變化時的檢測概率，1000次蒙特卡羅仿真的結果如圖6所示。當信噪比高于7 dB時，兩種算法的檢測概率均為1，可以準確地對多個目標的速度進行估計；隨著輸入信噪比的降低，檢測概率逐漸下降。當信噪比低于2 dB時，文獻[13]中算法的檢測概率降至0，而采用本文算法的檢測概率為0.8，仍然可以對目標進行參數估計；直至信噪比降低到–3 dB時，本文算法的檢測概率也降為0，無法同時對多個目標速度進行估計。相比于文獻[13]中的算法，本文所提算法對輸入信噪比的要求降低了約5 dB，更有利于微弱目標的檢測與參數估計。

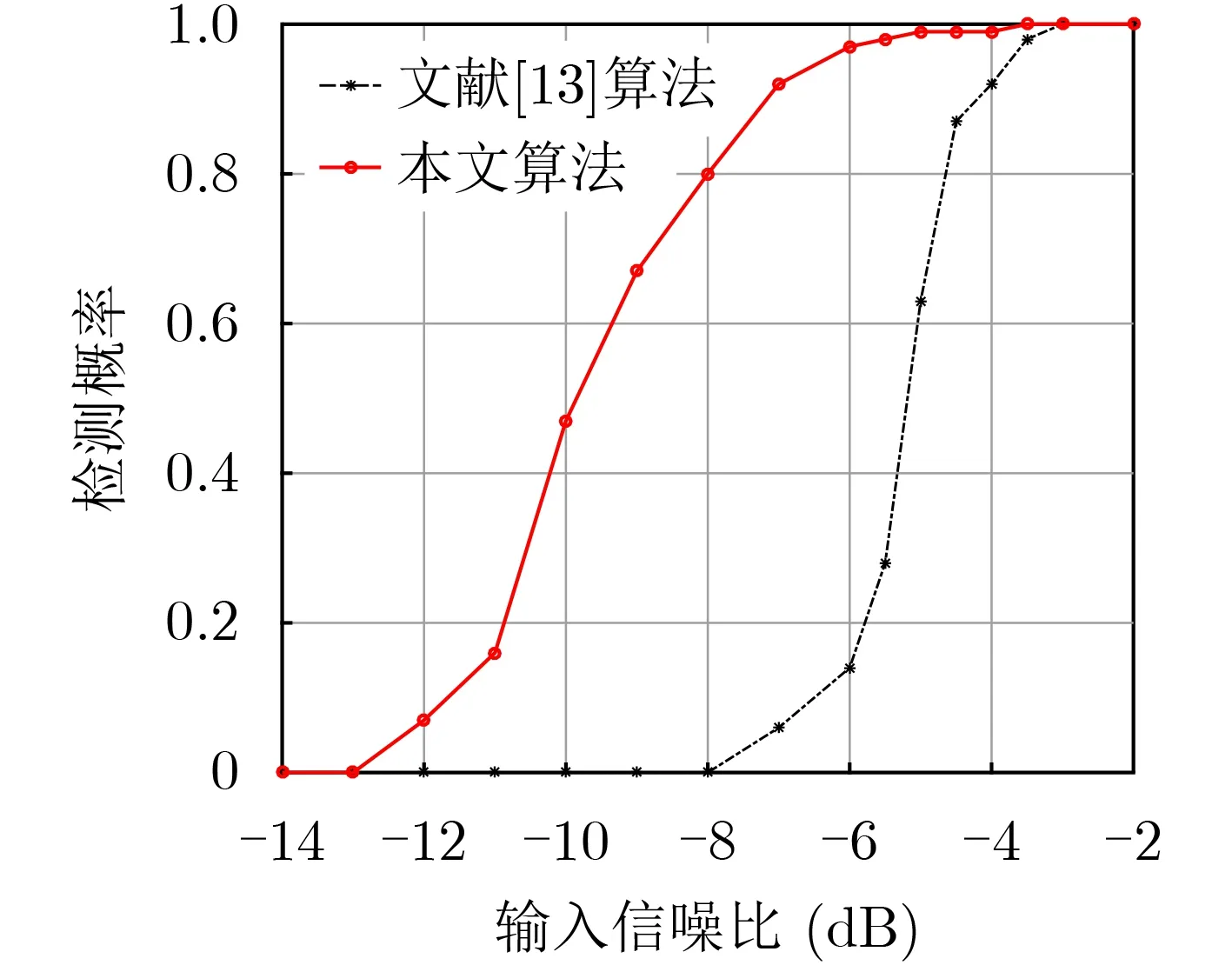
圖6 信噪比對檢測概率的影響

此外，目標本身的速度也會影響其相對估計誤差。設定輸入信噪比為–26 dB(輸出信噪比為2 dB)，分析不同速度下的相對估計誤差，作1000次蒙特卡羅仿真，結果如圖7所示。與文獻[13]中所提算法類似，隨著目標自身速度的增大，相對誤差逐漸減小。然而，對比兩條曲線可以看出當目標速度相同時，本文算法的相對誤差大于文獻[13]算法。當目標速度大于1000 m/s時，文獻[13]算法的相對誤差小于0.1%，可以忽略不計；而同樣要使相對誤差小于0.1%，本文算法則要求目標速度大于4000 m/s。

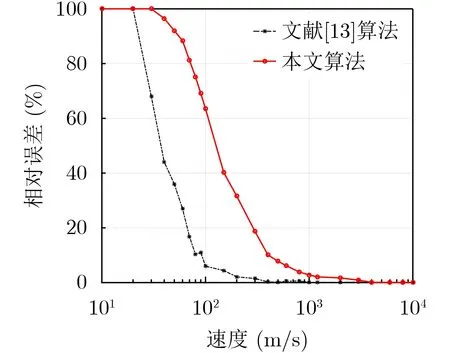
圖7 目標速度對估計誤差的影響

通過本文所提算法對多個目標的速度進行估計，其均方根誤差(Root-Mean-Square Error, RMSE)隨輸出信噪比的變化曲線如圖8所示。可以看出與文獻[12]相比，本文算法具有更好的估計精度，隨著信噪比的增大，其RMSE越接近于Cramer-Rao下限。

綜合圖6–圖8可以看出本文所提高速運動目標的參數估計算法更適用于低信噪比的情況，且估計誤差更小。

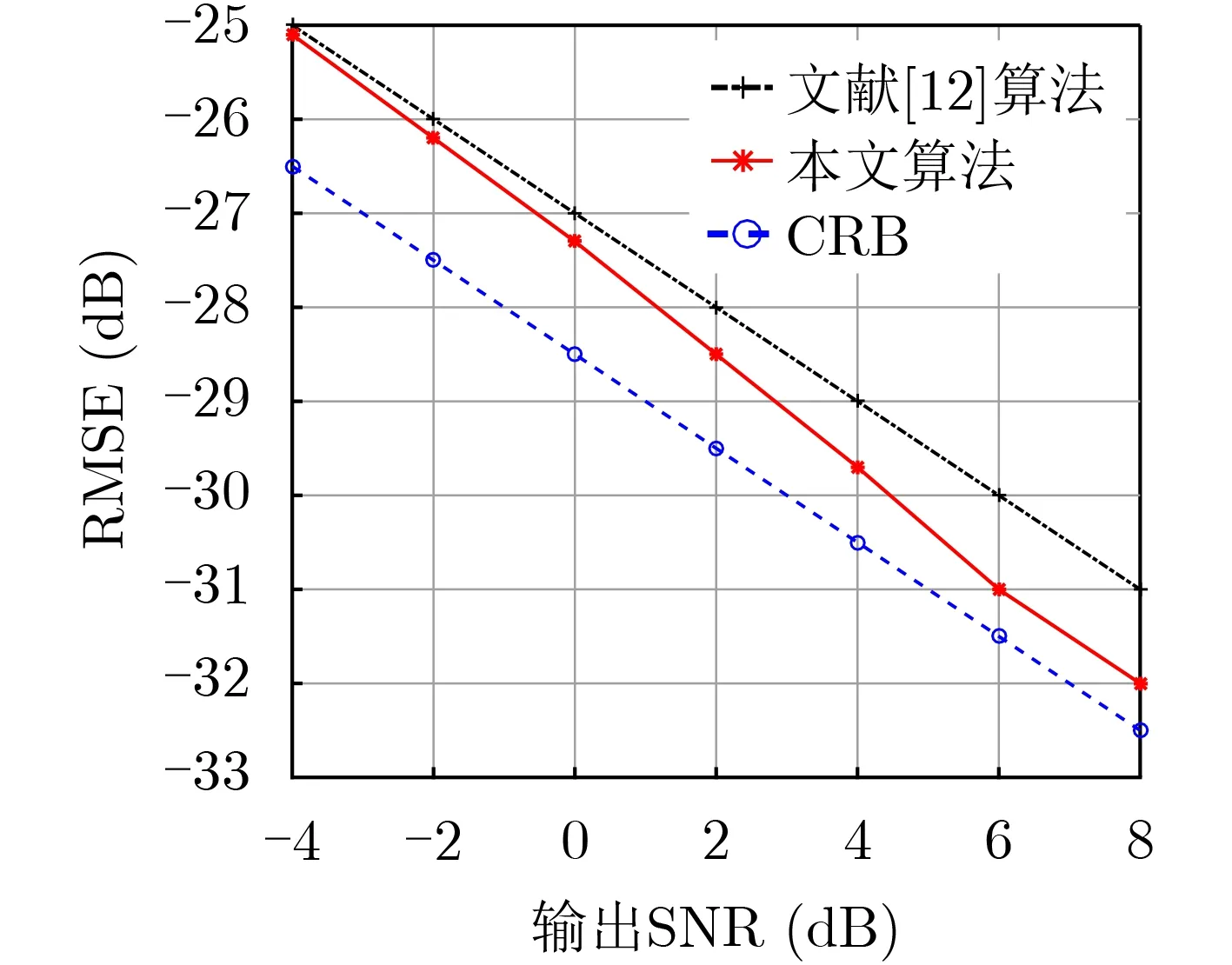
圖8 輸出SNR對RMSE的影響

6 結束語

針對現代電子戰場中雷達對目標檢測與參數估計的迫切需求，本文提出了一種基于Ransac算法的FA-OFDM雷達高速多目標參數估計的方法。依據FA-OFDM信號的大帶寬特性，采用IAA方法合成各個脈沖時刻的目標高分辨距離，再采用Ransac算法進行多直線擬合，實現對高速運動的多目標進行同時參數估計。相比文獻[13]所提算法，本文算法對輸入信噪比的要求降低了約5 dB，并且當目標速度大于4000 m/s時，速度估計的相對誤差小于0.1%，更有利于對低信噪比條件下高速運動目標的參數估計。