《數學分析》課程思政建設初探

李秀仙

(天津商業大學 理學院， 天津 300222)

1 引言

在2016年召開的全國高校思想政治工作會議上，習近平總書記發表重要講話，強調高等學校“要堅持把立德樹人作為中心環節，把思想政治工作貫穿教育教學全過程”，高校的思想政治工作“要用好課堂教學這個主渠道，思想政治理論課要堅持在改進中加強，……其他各門課都要守好一段渠、種好責任田，使各類課程與思想政治理論課同向同行，形成協同效應”[1]。這標志著課程思政思想的正式誕生。2017年，中共教育部黨組在《高校思想政治工作質量提升工程實施綱要》中要求大力推動課程思政建設，充分發揮課程的育人功能，在專業課程的教學過程中實現思政教育與知識教育的統一[2]。2020年，教育部印發《高等學校課程思政建設指導綱要》，要求根據專業特點和課程特點分類推進課程思政建設。綜上所述，課程思政建設已經成為我國高等教育領域的一個基本政策要求。

但從現實來看，由于思想政治教育的內容傳統上屬于人文社會學科領域，在文理分科的大背景下，很多理工類課程的教師感到難以將思想政治教育內容融入理工類專業課程的教學過程之中。為了推動理工類專業課程思政建設，本文以《數學分析》為例，討論在理工科類專業課程中如何進行課程思政建設。

2 《數學分析》課程思政元素的挖掘

挖掘課程的思政元素是進行課程思政建設的必要組成部分，也是課程思政建設的基礎。《數學分析》是數學、統計學等理工科專業的核心專業課程，是進一步學習概率統計、數值分析、復變函數論、常微分方程、大數據、機器學習、數據挖掘等后續課程的階梯。理論性強，抽象程度高是《數學分析》課程的基本特點。總的來說，《數學分析》中包含有比較豐富的課程思政元素。

2.1 唯物辯證法

辯證唯物主義是在總結自然科學、社會科學、思維科學的基礎上創立的思維方法論，數學是研究現實世界的空間形式和數量關系的科學。二者相互滲透、相互影響、相互促進[3，4]。例如在講極限概念的時候，都會引入魏晉時期的數學家劉徽首創割圓術的故事。也就是以“圓內接正多邊形的面積”，來無限逼近“圓面積”。劉徽形容割圓術為“割之彌細，所失彌少，割之又割，以至于不可割，則與圓合體，而無所失矣”。這同時也體現了“化圓為方”“化直為曲”的極限思想及“化整為零”“化零為整”的辯證統一，蘊含了“變與不變”“量變與質變”“近似與精確”的唯物辯證法思想。

2.2 科學倫理

微積分學是人類認識宇宙的發明創造，是牛頓、萊布尼茨分別獨立發現并證明的。萊布尼茨在解決曲線斜率，牛頓在求變速運動瞬時速率時發現了導數的概念，以他們當時的數學背景是解決不了該問題的，然后他們獨自探索，發現極限在解決該問題的重要性，由此形成了微積分理論。牛頓、萊布尼茨敢于探索真理、疑古求是，這種科學學術倫理觀值得學習。要善于在處理實際問題的過程中發現內在邏輯，知其然，還要知其所以然。

2.3 科學精神

歷史上，許多數學家都對《數學分析》的形成和發展做出了重要貢獻。這些數學家身上普遍閃耀著濃濃的科學精神[5]。比如，19世紀挪威著名數學家阿貝爾，生前窮困潦倒，在他的國家不被重視，無法獲得固定教席以專心于研究。只能靠為學生補習功課糊口，而且常常入不敷出，更不幸的是他于生命后期染上肺結核。盡管如此，他仍然不畏艱苦，勇攀知識高峰，在數學分析領域不僅創造了以他名字命名的“阿貝爾函數”、級數斂散性的“阿貝爾判別法”、反常積分斂散性的“阿貝爾判別法”“阿貝爾極限定理”“阿貝爾部分和公式”等，而且證明了除特殊情況之外五次或以上代數方程的根式解并不存在，從而解決了困擾數學界250年之久的世界性難題。《數學分析》課程中類似的思政元素并不鮮見，是對學生進行科學精神教育的良好素材。

2.4 數學之美

《數學分析》課程中處處體現著數學之美。數學美體現在很多方面，如數學的和諧統一之美[6]。眾所周知，向量是一個幾何概念，既有大小又有方向。開始，是用三角形法則或平行四邊形法則學習向量的和、差、數乘運算。笛卡爾空間直角坐標系的引入，使得空間中的任何向量可以用一個三維坐標來表示。這樣就將幾何問題轉化為了代數問題，在向量空間里求向量的各種運算就迎刃而解。這體現了幾何與代數的和諧統一。《數學分析》課程內容中類似的情況還有很多，譬如拉格朗日中值定理建立了整體與局部的統一；牛頓-萊布尼茨公式建立了微分與積分的辯證統一。從數學美的角度，挖掘課程思政元素，為在《數學分析》課程中實施課程思政教學奠定了基礎。

2.5 中華優秀傳統文化

作為一種文化，數學具有民族性、地域性。以我國為例，蒙古族的蒙古包及服飾在設計上符合黃金比例結構，看起來更美觀。維吾爾族的傳統服飾、手工藝品好多都是按照幾何圖形繪制而成；藏族的建筑、壁畫與軸對稱、中心對稱的思想相一致[7]。可以說，包括《數學分析》在內的各門數學課程中都蘊含了豐富的中華優秀傳統文化基因。這些是進行課程思政建設的寶貴財富。

3 《數學分析》課程思政的實施

在《數學分析》的教學過程中，根據教學內容的特點，采取多種方法，將課程思政建設真正落到實處。

3.1 延伸講授法

所謂延伸講授是指在講清楚基本知識之后，按照課程思政的方向性要求，對所講授的知識適當地進行延伸性的講解，直接揭示數學知識中所蘊含的思政道理。

例如梯度的概念引入。金屬片原點放有一只蠟燭，一只小螞蟻在受熱的金屬片某點處，問小螞蟻沿著什么方向跑，可以最快到達涼快的地？答案是沿著梯度的方向。什么是梯度呢？數學上，梯度的定義是這樣的[8]：

若f(x,y,z)在點P0(x0,y0,z0)存在對所有自變量的偏導數，則稱向量(fx(P0),fy(P0),fz(P0))為函數f在點P0的梯度，記作

gradf(P0)=(fx(P0),fy(P0),fz(P0))

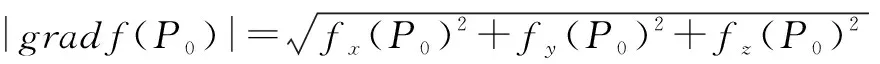
從梯度概念易知，梯度方向是等值線上的法向量。從這個數學概念中可以得到啟迪：人生要有規劃，不能無頭蒼蠅亂竄，碰到人生十字路口，也要善于思考。目前，梯度的思想被用在機器學習上，沿著誤差函數梯度反方向更新參數，誤差下降得最快，也就是能最快達到算法精度。

3.2 故事教學法

部分學生對學習《數學分析》這么抽象的課程本身有種畏難情緒，而在教學過程中將故事融入教學是一種有效扭轉這種局面的方法[9]。

在講授第一型曲線積分時，會講到心形線。心形線有參數式、極坐標式、直角坐標式三種表達。為更好地讓同學們了解該曲線，可以穿插一個美麗傷感的愛情故事。一個窮困潦倒的數學家與國王的女兒戀愛，遭到了國王的反對。于是強硬地拆散他們，把數學家驅散出境。在這個數學家去世前給公主寄了一封信，但是信上只有一個數學式子。除了公主，沒人知道這個數學式子代表什么意思。公主拿出筆，按照數學式畫起圖來……這是一顆心的形狀，表達了數學家臨死前都愛著公主。這個凄美的故事告訴大學生，學好數學原來可以這么唯美的表達情感。多向學生介紹這樣的數學故事同時可以提高課程趣味性。

3.3 情境教學法

情境教學法就是在課程學習過程中，結合學習內容，提供或者創設相關情境，通過情境展現數學知識中的思政要素，進行思政教育。

例如，在講授曲面積分中曲面的側的概念時，都會介紹單側曲面，同學們對這個概念比較模糊。不同于現實中所見的雙側曲面，單側曲面只有一個面和一個邊。單側曲面比較典型的代表是莫比烏斯帶[10]。莫比烏斯帶是德國數學家與天文學家莫比烏斯發現的。這條帶子是由一張長方形的紙扭轉半圈兩頭粘在一起做成的。此時可以現場演示，培養同學們動手能力。然后用鋼筆在這條帶子上畫一圈，畫的過程中提示同學們該紙帶沒有翻面，再打開會發現繞長方形紙的上下兩面同時畫上了線。同學們不禁會想，為什么呢，難道與單側曲面有關？再引導大家，如果一個小螞蟻繞著你的水瓶外側走，水瓶密封的情況下它能走到里側嗎？顯然不能。如果你的水瓶做成莫比烏斯帶呢？同學們會恍然大悟，莫比烏斯帶，小螞蟻可以輕松不翻面走遍帶子每一處地方。這時候我們可以引導莫比烏斯帶像不像數學符號？它不但外表像，而且當一個人站在巨大的莫比烏斯帶上沿著它的面走著，那么他永遠走不到盡頭，因此莫比烏斯帶常被聯系為無窮的代表。然后在PPT上展示幾張莫比烏斯帶造型的建筑，譬如鳳凰國際傳媒中心、湖南長沙龍王港大橋、哈薩克斯坦的新國家圖書館等。接著可以舉現實中磁帶的例子，磁帶做成莫比烏斯帶，可以避免翻面，減少摩擦，延長使用壽命。同學們感悟數學與現實生活中美的聯系，加強學生的美育教育，使他們在美的享受中對這節課的內容產生強烈的求知欲。