氣彈簧助力式四連桿鉸鏈發(fā)動機(jī)罩的計算與優(yōu)化分析
侯林 史承婕 王鵬 王海歌
(一汽奔騰轎車有限公司奔騰開發(fā)院,長春 130012)
1 前言
氣彈簧助力式四連桿鉸鏈發(fā)動機(jī)罩系統(tǒng)早期在轎車上較少應(yīng)用。此種發(fā)動機(jī)罩可以實現(xiàn)更復(fù)雜的運(yùn)動軌跡,造型上可以突破現(xiàn)有定軸鉸鏈?zhǔn)桨l(fā)動機(jī)罩的一些限制,隨著汽車造型的不斷豐富,此類發(fā)動機(jī)罩應(yīng)用日益廣泛。隨著需求的增加,對此種發(fā)動機(jī)罩系統(tǒng)的應(yīng)用研究也提出了更高的要求。
目前,關(guān)于氣彈簧助力式機(jī)構(gòu)的研究主要分為2個方向:一是定軸鉸鏈機(jī)構(gòu),結(jié)構(gòu)簡單、普遍應(yīng)用于尾門,這方面理論計算分析成果豐富[1-6];二是四連桿機(jī)構(gòu),結(jié)構(gòu)復(fù)雜,一般應(yīng)用于發(fā)動機(jī)罩或行李箱上,這方面計算分析成果相對較少[7-8]。本文借鑒上述2 方向的研究成果,細(xì)化氣彈簧助力式四連桿機(jī)構(gòu)的理論分析和驗證過程,并給出開閉操作力等參數(shù)優(yōu)化方向,為后續(xù)布置參數(shù)自動優(yōu)化提供參考。
2 發(fā)動機(jī)罩四連桿鉸鏈的機(jī)構(gòu)布置與設(shè)計
2.1 機(jī)構(gòu)布置
發(fā)動機(jī)罩四連桿鉸鏈的布置需要綜合考慮運(yùn)動校核、剛度性能、空間利用和外觀等多方面的要求,主要體現(xiàn)在2個方面:
a.四連桿鉸鏈的布置位置與定軸鉸鏈布置類似,需要盡量增大在整車Y向上的尺寸,以利于保證發(fā)動機(jī)罩獲得更大的整體剛度,并盡量在整車X向上靠近車后方向,以利于發(fā)動機(jī)罩運(yùn)動校核。
b.固定方式主要有2種,即水平安裝、整車Z向固定和側(cè)向安裝、Y向固定。前者的優(yōu)點(diǎn)是鉸鏈處無需遮蔽,車身側(cè)無孔洞,缺點(diǎn)是鉸鏈Z向不可調(diào),易造成發(fā)動機(jī)罩間隙段差不良;后者如圖1 所示,優(yōu)點(diǎn)是鉸鏈Z向可調(diào),方便調(diào)整發(fā)動機(jī)罩的間隙段差,缺點(diǎn)是鉸鏈處難以遮蔽,車身側(cè)存在孔洞。
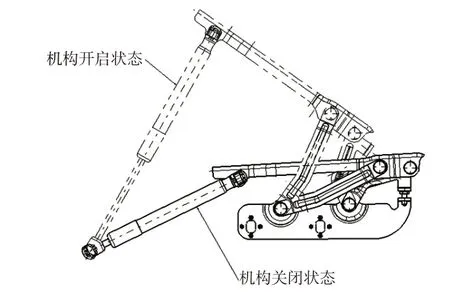
圖1 氣彈簧助力式四連桿鉸鏈開啟機(jī)構(gòu)
2.2 機(jī)構(gòu)設(shè)計
機(jī)構(gòu)設(shè)計主要應(yīng)滿足發(fā)動機(jī)罩的運(yùn)動軌跡要求,具體包括:
a.四連桿長度的設(shè)計,主要通過CATIA 軟件,應(yīng)用作圖解析法進(jìn)行。
b.四連桿鉸鏈的瞬心設(shè)計,圖2 所示為某車型開發(fā)完成后四連桿鉸鏈的瞬心軌跡,發(fā)動機(jī)罩X向坐標(biāo)最大值需保證在瞬心軌跡內(nèi)側(cè),這主要是為了保證發(fā)動機(jī)罩后點(diǎn)的運(yùn)動軌跡向上。
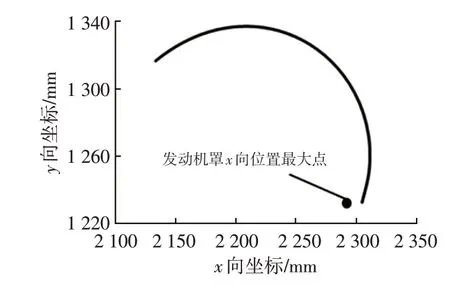
圖2 四連桿鉸鏈瞬心軌跡示意
3 發(fā)動機(jī)罩開閉操作力分析
3.1 發(fā)動機(jī)罩的力學(xué)分析模型
圖3 所示為某車型的發(fā)動機(jī)罩受力分析模型,其中,A、B、C、D為四連桿鉸鏈的4 個旋轉(zhuǎn)軸心,S1、S2為氣彈簧的固定點(diǎn),T為鉸鏈機(jī)構(gòu)的瞬心,H為開、閉發(fā)動機(jī)罩的操作點(diǎn),在ZX平面內(nèi)進(jìn)行發(fā)動機(jī)罩開啟和關(guān)閉過程中的操作力分析。
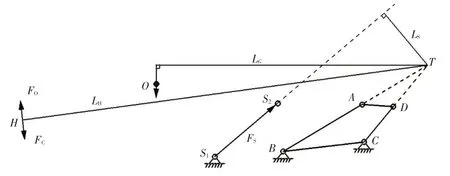
圖3 發(fā)動機(jī)罩力學(xué)分析模型
發(fā)動機(jī)罩開啟過程中:

式中,MG為發(fā)動機(jī)罩重力矩;Mh為鉸鏈阻力矩;MO為發(fā)動機(jī)罩開啟操作力力矩;MS為氣彈簧力矩。
則:
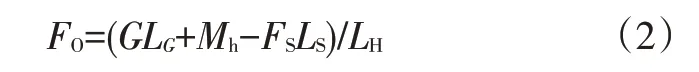
式中,F(xiàn)O為發(fā)動機(jī)罩開啟操作力;G、LG分別為發(fā)動機(jī)罩重力及其力臂;FS、LS分別為氣彈簧輸出力及其力臂;LH為發(fā)動機(jī)罩開閉力臂。
發(fā)動機(jī)罩關(guān)閉過程中:

式中,MC為發(fā)動機(jī)罩關(guān)閉操作力力矩。
則:
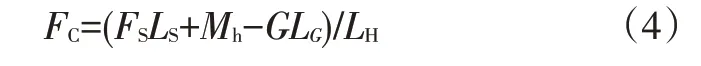
式中,F(xiàn)C為發(fā)動機(jī)罩關(guān)閉操作力。
為了計算發(fā)動機(jī)罩的開閉操作力,需要先求解發(fā)動機(jī)罩的旋轉(zhuǎn)中心T(瞬心)的位置,再由此計算MG、MS等相關(guān)力矩。
3.2 四連桿機(jī)構(gòu)的運(yùn)動求解
為了求解四連桿機(jī)構(gòu)的瞬心位置,需要對四連桿機(jī)構(gòu)的各運(yùn)動參數(shù)進(jìn)行求解。如圖4所示,已知四連桿機(jī)構(gòu)的各初始角度分別為Φ1、Φ2、Φ3、Φ4,各連桿長度分別為LAB、LBC、LCD、LAD,需求解發(fā)動機(jī)罩在開閉運(yùn)動過程中四連桿內(nèi)部角度變化情況。取Φ1為角度自變量,則機(jī)構(gòu)內(nèi)其他角度為:
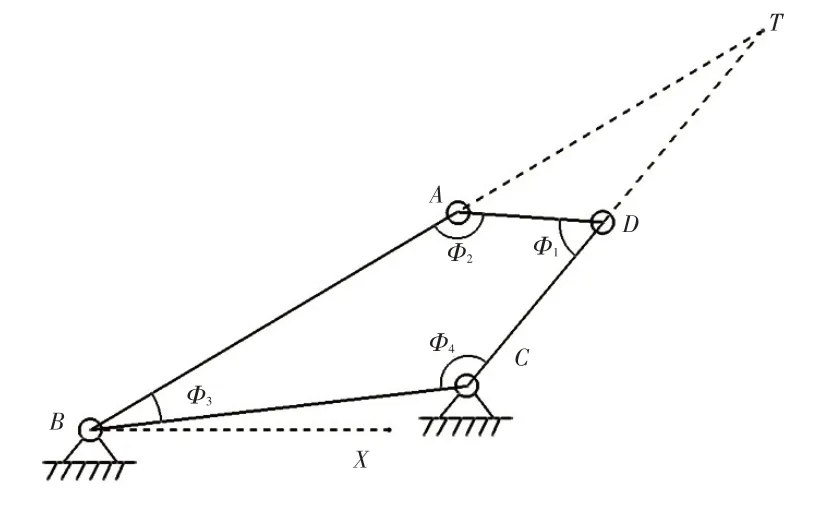
圖4 四連桿機(jī)構(gòu)運(yùn)動分析模型
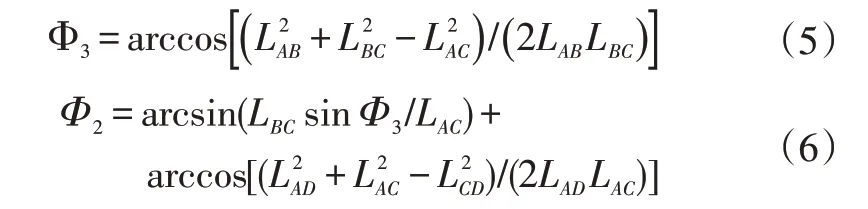
則Φ4=2π-Φ1-Φ2-Φ3。
3.3 四連桿鉸鏈的瞬心坐標(biāo)計算
瞬心位置的計算可以根據(jù)文獻(xiàn)[9]確定,對于圖4中的T點(diǎn)位置,設(shè)其坐標(biāo)為(XT,ZT),則:
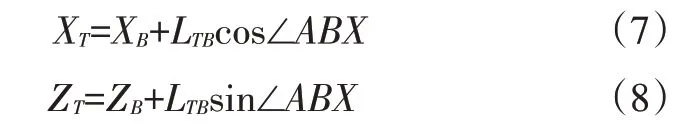
式中,(XB,ZB)為鉸鏈的旋轉(zhuǎn)軸心B的坐標(biāo);LTB=LTA+LAB為瞬心T與旋轉(zhuǎn)軸心B的距離;LTA=LADsin(π-Φ1)/sin(π-Φ3-Φ4)為瞬心T與旋轉(zhuǎn)軸心A的距離;∠ABX=arctan[(ZC-ZB)/(XC-XB)]+Φ3;(XC,ZC)為鉸鏈的旋轉(zhuǎn)軸心C點(diǎn)坐標(biāo)。
3.4 重力矩的計算
圖5 所示為重力矩分析模型,先求取質(zhì)心點(diǎn)坐標(biāo),然后求取重力臂,最后求取重力矩。設(shè)質(zhì)心O點(diǎn)坐標(biāo)為(XO,ZO),旋轉(zhuǎn)軸心A點(diǎn)坐標(biāo)為(XA,ZA),則:
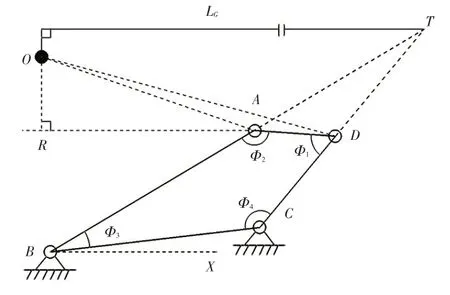
圖5 重力矩分析模型
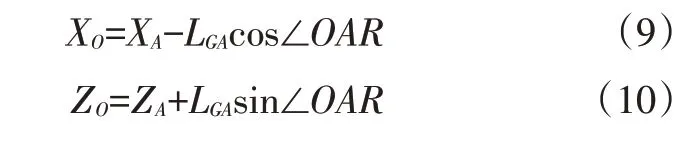
式中,XA=XB+LABcos∠ABX;ZA=ZB+LABsin∠ABX;LGA為質(zhì)心O與旋轉(zhuǎn)軸心A的距離;∠OAR=2π-∠OAD-Φ2-∠ABX;;LGD為質(zhì)心O與旋轉(zhuǎn)軸心D的距離。
根據(jù)以上參數(shù)可求得重力臂LG=XT-XO,重力矩MG=G(XT-XO)。
3.5 氣彈簧力矩的計算
3.5.1 氣彈簧力臂的計算
圖6 所示為氣彈簧力臂分析模型。氣彈簧力臂LS=LS2Tsin∠S1S2T,LS2T為氣彈簧發(fā)動機(jī)罩固定點(diǎn)與瞬心間的距離。參考發(fā)動機(jī)罩質(zhì)心坐標(biāo)的推導(dǎo)過程,可得到發(fā)動機(jī)罩任意開度下的氣彈簧安裝點(diǎn)坐標(biāo)S2(XS2,ZS2)。則:
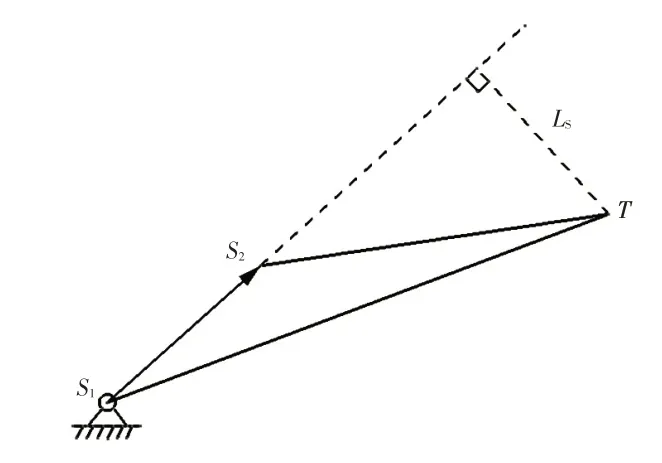
圖6 氣彈簧力臂分析模型
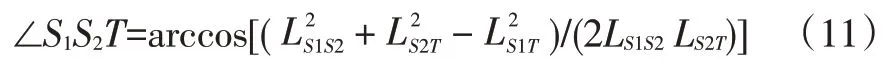
式中,LS1S2為氣彈簧固定點(diǎn)間的距離;LS1T為氣彈簧車身固定點(diǎn)與瞬心之間的距離。
3.5.2 氣彈簧輸出力的計算
氣彈簧的反力特性如圖7所示,圖中F1、F2、F3、F4為氣彈簧特性力,Le為氣彈簧行程,C1、C2分別為測力點(diǎn)。在確定氣彈簧輸出力時,首先要確定系統(tǒng)所需的最小氣彈簧力,然后根據(jù)氣彈簧的輸出力特性,求得發(fā)動機(jī)罩在開、閉過程中氣彈簧的力矩MS。
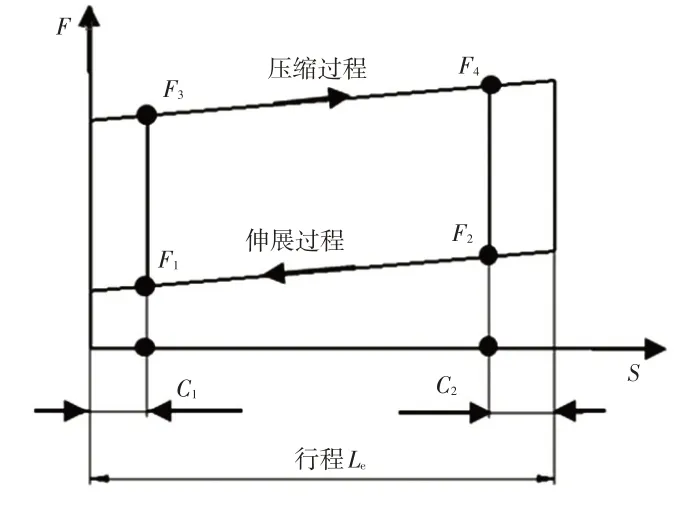
圖7 氣彈簧輸出力特性
3.5.2.1 氣彈簧輸出力最小值的確定
發(fā)動機(jī)罩開閉操作力在高溫、常溫和低溫條件下具有不同的工程目標(biāo)要求。首要是保證發(fā)動機(jī)罩在極端低溫環(huán)境下(-30 ℃)不會掉落傷人,所以將該工作條件下氣彈簧設(shè)計需要滿足的力設(shè)置為氣彈簧輸出力最小值。在此條件下,氣彈簧輸出力最小值與設(shè)計目標(biāo)的關(guān)系為:
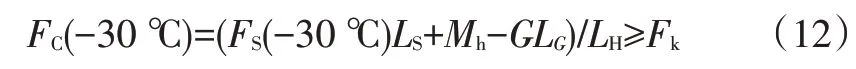
式中,F(xiàn)C(-30 ℃)為-30 ℃條件下氣彈簧保證撐起發(fā)動機(jī)罩的最小壓縮力;Fk為在-30 ℃條件下關(guān)閉發(fā)動機(jī)罩所需要預(yù)留的操作力安全余量,為設(shè)計目標(biāo)值。
式(12)取等號時,F(xiàn)S(-30 ℃)=(FkLH-Mh+GLG)/LS,綜合理想氣體狀態(tài)方程pV=nRT和壓強(qiáng)公式F=pS,并根據(jù)氣彈簧工作原理,推導(dǎo)可知:

式中,Tl為指定的開氏低溫條件;Fl為Tl溫度條件下的氣彈簧力;Th為指定的開氏高溫條件;Fh為Th溫度條件下的氣彈簧力。
根據(jù)式(13),由低溫(-30 ℃)狀態(tài)下的FS(-30 ℃)可以推導(dǎo)出常用的常溫(20 ℃)、高溫(80 ℃)狀態(tài)下的氣彈簧力。
3.5.2.2 氣彈簧動態(tài)行程中輸出力的計算
參考文獻(xiàn)[7],氣彈簧在不同行程位置的反力分別為F2=KF1、F3=F1+2f、F4=F2+2f。其中,K為氣彈簧剛度系數(shù),f為氣彈簧摩擦力。根據(jù)行程與力的比例關(guān)系,可以得到隨氣彈簧行程變化的輸出力為:
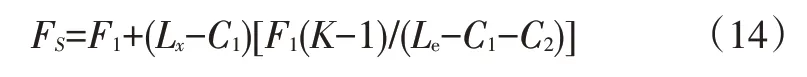
式中,Lx為氣彈簧的行程變量。
3.6 鉸鏈阻力矩的計算
四連桿的鉸鏈阻力矩Mh一般很小,且難以計算。一般可以根據(jù)類似鉸鏈的阻力矩進(jìn)行設(shè)定,也可以通過試驗測定。
3.7 發(fā)動機(jī)罩開閉操作力計算
如圖3所示,根據(jù)式(2)、式(4)轉(zhuǎn)化,可以求得發(fā)動機(jī)罩開啟操作力為:

發(fā)動機(jī)罩關(guān)閉操作力為:
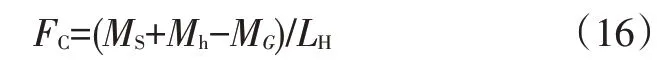
4 基于Excel軟件的編程與試驗驗證
4.1 基于Excel軟件的編程
根據(jù)上述計算分析,應(yīng)用Excel 軟件編制了開啟機(jī)構(gòu)的計算程序,其輸入界面如圖8、圖9所示。

圖8 機(jī)構(gòu)參數(shù)輸入界面

圖9 氣彈簧參數(shù)輸入界面
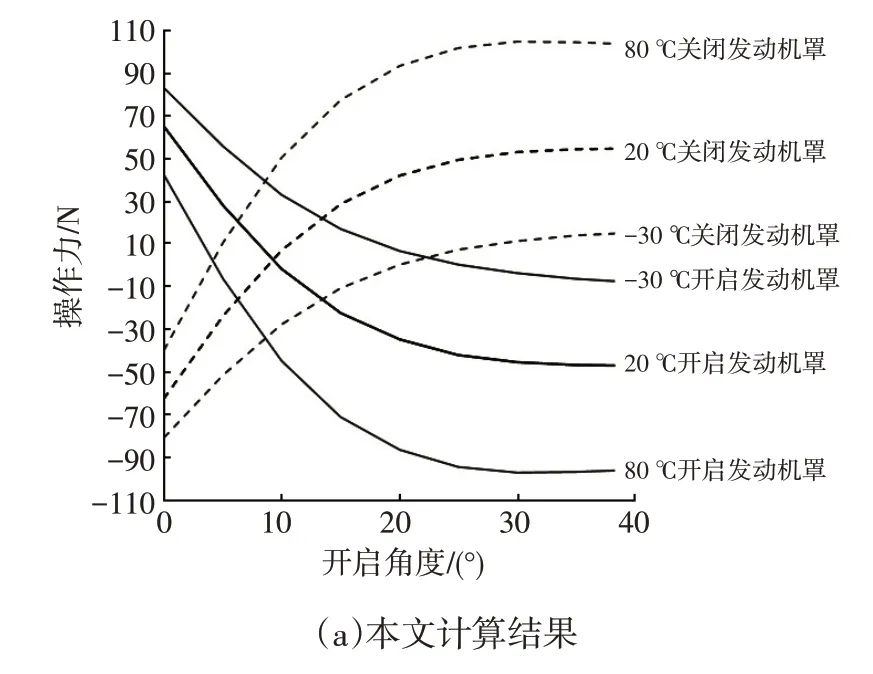
程序可以輸出氣彈簧特性力、行程、發(fā)動機(jī)罩開啟和關(guān)閉的最大力、開閉操作力曲線圖等。本文和國內(nèi)某主流供應(yīng)商針對某車型發(fā)動機(jī)罩開閉操作力的計算曲線輸出結(jié)果如圖10 所示,各溫度下輸出曲線符合度在95%以上。
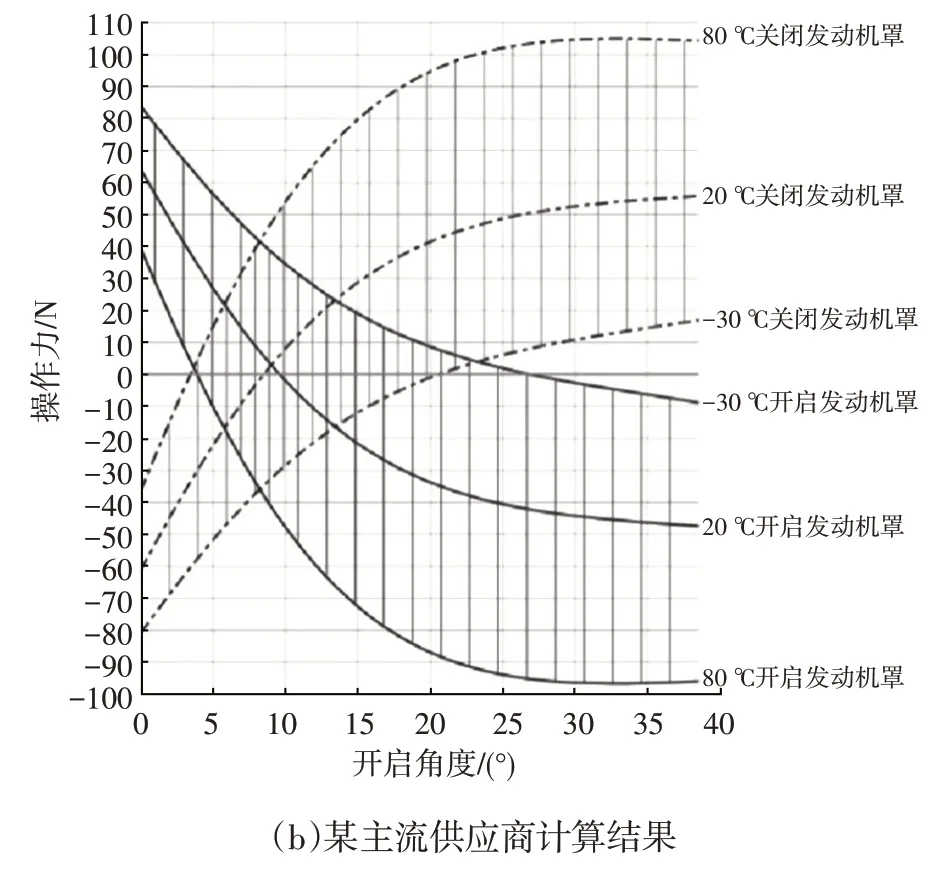
圖10 某車型發(fā)動機(jī)罩開閉操作力曲線
4.2 試驗驗證
針對計算結(jié)果,選定某車型進(jìn)行開閉操作力計算符合度的實車驗證,試驗環(huán)境溫度為20 ℃,試驗用氣彈簧力為中值樣件(力值偏差<5 N),試驗車發(fā)動機(jī)罩全開角度為38.5°,試驗結(jié)果如表1所示。由于實車發(fā)動機(jī)罩開啟時,鎖體會將其彈起約0.8°,故實測數(shù)據(jù)從0.8°開始。
由表1 可知,在累積實車各項偏差后,計算的最大試驗偏差在20%以內(nèi),可以為后續(xù)實車開發(fā)分析提供設(shè)計參考。
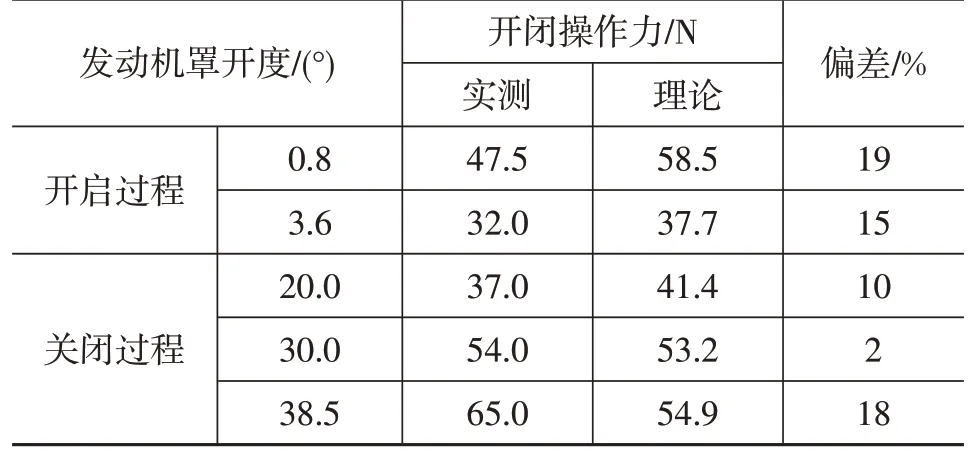
表1 發(fā)動機(jī)罩開閉操作力試驗結(jié)果
5 計算結(jié)果的優(yōu)化分析
發(fā)動機(jī)罩助力開啟機(jī)構(gòu)設(shè)計中重點(diǎn)關(guān)注開啟和關(guān)閉操作力的大小、平衡角度的位置等影響用戶體驗的參數(shù)。初步計算輸出的結(jié)果往往不能同時滿足高溫、常溫、低溫的開閉操作力工程目標(biāo)要求,為了獲取更優(yōu)的結(jié)果,需要對計算參數(shù)進(jìn)行優(yōu)化。
5.1 發(fā)動機(jī)罩關(guān)閉操作力的優(yōu)化分析
以常溫下發(fā)動機(jī)罩的關(guān)閉操作力為例進(jìn)行分析。
式(16)中,Mh很小,可以忽略,得到常溫下操作力為:
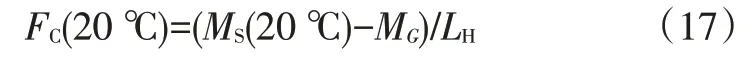
低溫下,有MS(-30 ℃)=FkLH+MG,由式(13)變形可得:

將式(19)代入式(17),整理可得:

根據(jù)式(20),可以得出以下結(jié)論:
a.發(fā)動機(jī)罩在常溫下的關(guān)閉操作力,只與MG、LH、Fk有關(guān),與LS無關(guān),即通過調(diào)整氣彈簧安裝點(diǎn)的位置無法改變常溫下關(guān)閉操作力的大小。
b.減小常溫關(guān)閉操作力,可以通過減小Fk、MG或增大LH實現(xiàn),但發(fā)動機(jī)罩結(jié)構(gòu)一旦確定,MG和LH很難調(diào)整。所以實際應(yīng)用中,調(diào)整關(guān)閉操作力的主要手段是犧牲部分Fk值。
5.2 發(fā)動機(jī)罩開啟操作力的優(yōu)化分析
由式(2)、式(19)可知,在MG和Fk不變的條件下,MS為定值,F(xiàn)S從發(fā)動機(jī)罩全開到全閉的變化率可以用Y表示,其值一般在1.1~1.4 范圍內(nèi),讀取Excel 程序中的氣彈簧力臂LS的變化率Ys為2.4左右,即Ys≈2Y。這意味著在全開位置MS一定的條件下,LS所占的比值越高,MS到全閉位置的衰減越快,即需要更大的開啟操作力才能打開發(fā)動機(jī)罩。全開與全閉位置的LS的變化方向一致,所以當(dāng)關(guān)閉操作力一定時,可以通過增大LS來增大發(fā)動機(jī)罩開啟操作力,減小LS來降低發(fā)動機(jī)罩開啟操作力。這可以通過調(diào)整氣彈簧的安裝位置來實現(xiàn)。
5.3 發(fā)動機(jī)罩開啟和關(guān)閉平衡角度的優(yōu)化分析
由發(fā)動機(jī)罩開啟操作力的分析過程和結(jié)果可得:當(dāng)關(guān)閉操作力一定時,增大開啟操作力,發(fā)動機(jī)罩開啟的平衡角度增大,反之,發(fā)動機(jī)罩開啟的平衡角度減小。根據(jù)上述結(jié)論可以調(diào)整優(yōu)化發(fā)動機(jī)罩開啟和關(guān)閉的平衡角度。
5.4 氣彈簧剛度系數(shù)K的優(yōu)化分析
K一般由供應(yīng)商提供,當(dāng)無法對MG、LH、固定點(diǎn)位置等參數(shù)進(jìn)行優(yōu)化時,可以考慮對K進(jìn)行優(yōu)化。根據(jù)K=F2/F1、理想氣體狀態(tài)方程和氣彈簧工作原理,可以推得:

式中,V1為發(fā)動機(jī)罩全閉時氣彈簧伸展?fàn)顟B(tài)下的氣體工作體積;V2為發(fā)動機(jī)罩全開時氣彈簧壓縮狀態(tài)下的氣體工作體積。
由式(21)可知:如需減小K,可以同時增大V1和V2,即增加氣彈簧缸筒的長度。由于受限于氣彈簧布置和內(nèi)部的結(jié)構(gòu)實現(xiàn)條件,調(diào)整空間有限,調(diào)整的效果并不明顯,所以建議在沒有其他更好優(yōu)化方式的情況下使用。通過Excel 程序測試,減小K可以使開閉操作力曲線更加平直,同時也可以增大開啟操作力FO。
5.5 鉸鏈軸心布置的優(yōu)化分析
鉸鏈各軸心的布置主要影響鉸鏈的瞬心位置,進(jìn)而影響各力臂及發(fā)動機(jī)罩的開閉操作力。本文對鉸鏈瞬心位置的變化對發(fā)動機(jī)罩開閉操作力的影響進(jìn)行分析。
5.5.1 關(guān)閉操作力
根據(jù)式(20)可知,當(dāng)Fk為定值時,F(xiàn)C與LG/LH正相關(guān),且有LG/LH<1,當(dāng)瞬心位置向車后方調(diào)整時,設(shè)調(diào)整量為Δx,可得:

隨著瞬心位置向車后方調(diào)整,LG/LH有增大趨勢,即FC會增大。但在實際調(diào)整中,Δx遠(yuǎn)小于LG和LH,其變化對關(guān)閉操作力的影響也很小,所以實際應(yīng)用時,調(diào)整瞬心位置對關(guān)閉操作力的影響可忽略不計。
5.5.2 開啟操作力
根據(jù)式(2)可知,F(xiàn)O=(GLG-FSLS)/LH(忽略鉸鏈阻力矩)。調(diào)整鉸鏈瞬心位置時,會導(dǎo)致多個變量變化,定量推導(dǎo)過于繁瑣,通過Excel程序定性分析可知,隨著瞬心的后移,F(xiàn)O逐漸下降。實際應(yīng)用中可通過調(diào)整瞬心位置來優(yōu)化FO。
6 結(jié)束語
本文針對目前氣彈簧助力式四連桿鉸鏈機(jī)構(gòu)應(yīng)用日益普遍的情況,提出了基于Excel 軟件編程的操作力計算方法,同時針對計算結(jié)果從理論的角度給出了優(yōu)化方向,包括開啟操作力、關(guān)閉操作力、平衡角度、四連桿鉸鏈軸心的優(yōu)化。本文計算方法的理論結(jié)果與國內(nèi)某主流供應(yīng)商的計算結(jié)果符合度在95%以上;與實車試驗值的最大偏差在20%以內(nèi);并首先從理論的角度給出操作力等的優(yōu)化分析,其優(yōu)化原理也適用于更簡單的氣彈簧助力式定軸鉸鏈背門或發(fā)動機(jī)罩的操作力分析。未來將在現(xiàn)有成果的基礎(chǔ)上,在參數(shù)自動優(yōu)化驅(qū)動的氣彈簧布置方向上開展更深入的研究。

