探究留痕，讓學生的思維看得見

易道榮

【摘 要】探索基于“學”的教學設計轉型要關注五個前提、三條路徑、三個目標。每個任務創設要圍繞“核心問題、教學目標、基于教材、基于學生、任務小目標”五個前提，通過創設“可學的材料”，經歷“可見的思維”，發現“可現的生長”，形成可學、可見、可現的任務路徑;達成讓不同層次學生學習介入、讓不同層次學生探究留痕、讓不同層次學生知識得以生長的學習目標。

【關鍵詞】探究留痕 思維看得見 教學轉型

在網絡線上教研期間，有幸參與南京市教研室組織的小數線上教研，探索基于學的“任務”教學設計轉型，帶給筆者深深的觸動。原本以為就是簡單圍繞目標設計幾個活動，創設幾個綜合練習，就可以達成轉型。殊不知，如何基于“學”，看似簡單卻不是那么的容易，以三年級下冊《小數的初步認識》一課為例，筆者設計修改，進行多次打磨改進。“如何面向全體，將任務融合成讓不同水平、不同層次學生都能介入并留下探究的印跡？”這是市教研員朱宇輝老師提出的建議，也為這節課的創設指明了方向。

基于此，筆者的新設計圍繞“介入與留痕，讓思維得以生長”這一創設主張，確立了兩個核心問題，認識零點幾和認識幾點幾;再設立了任務1-1、評價1-2、任務2-1和評價2-2。每個任務都是從三個方面考慮：一是創設“可學的材料”，二是經歷“可見的思維”，三是發現“可現的生長”。

一、創設“可學的材料”，讓不同層次學生介入學習

1.在新知探究中創設可學材料

（1）核心問題一：認識零點幾的創設

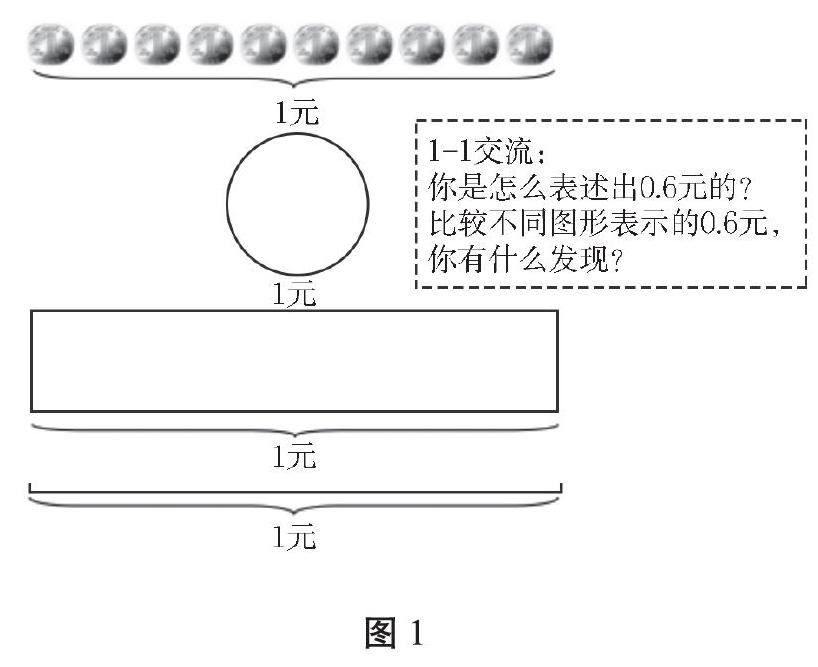
任務1-1（見圖1）的小目標是：經歷小數（零點幾）初步認識的過程，體會十分之幾元就是零點幾元。教材從長度入手，但基于學生的思考，商品價格相對于學生而言更熟悉，更能夠激發學生對已有小數認知的充分展現。于是，筆者從設計0.6元的商品標牌入手，創設學習任務1-1“選擇一個圖形來表示你認識的0.6元”。筆者提供給學生1角硬幣、圓形、長方形、線段圖這些學習材料，便于不同層次學生都能夠介入學習，進行有效的自主探究。學生保底可選擇硬幣圖進行探索，有經驗的學生可能會選擇長方形探索，抽象思維強的學生可以選擇線段圖探索。而且這里長方形、線段圖都與硬幣圖一樣長，巧妙地利用數形結合思想，建構便于學生探究的學習材料。可見，要讓不同層次學生介入學習，需要創設“可學的材料”。

（2）核心問題二：認識幾點幾的創設

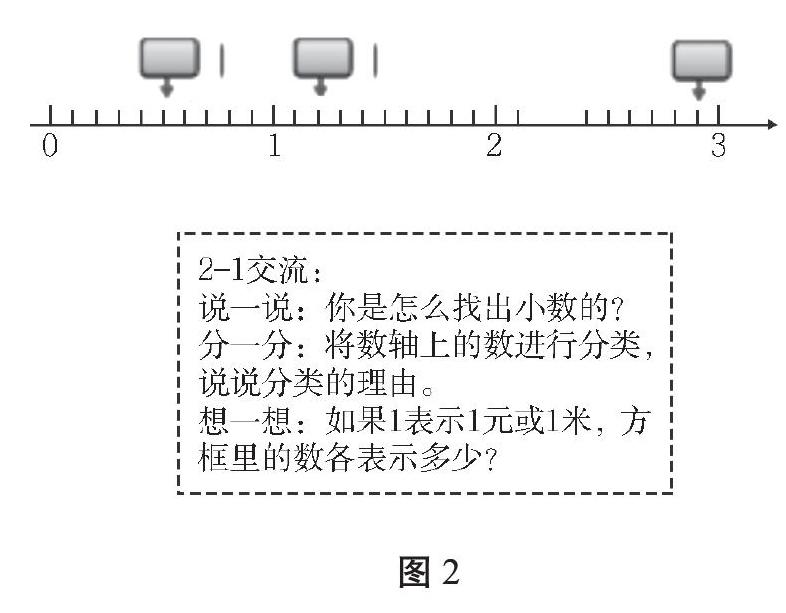
任務2-1（見圖2）的小目標是：經歷小數（幾點幾）含義的探究過程，認識小數各部分名稱。基于學生已經經歷零點幾的含義的理解，有自主突破嘗試探究幾點幾的基礎。于是筆者創設任務2-1在方框里填小數的活動，放手讓學生自主探究幾點幾，對于第一個小于1的小數所有學生都會填，而大于1的兩個小數，對于學生來說具有挑戰性。

2.在評價學習中創設可學材料

（1）基于核心問題一：認識零點幾的評價創設

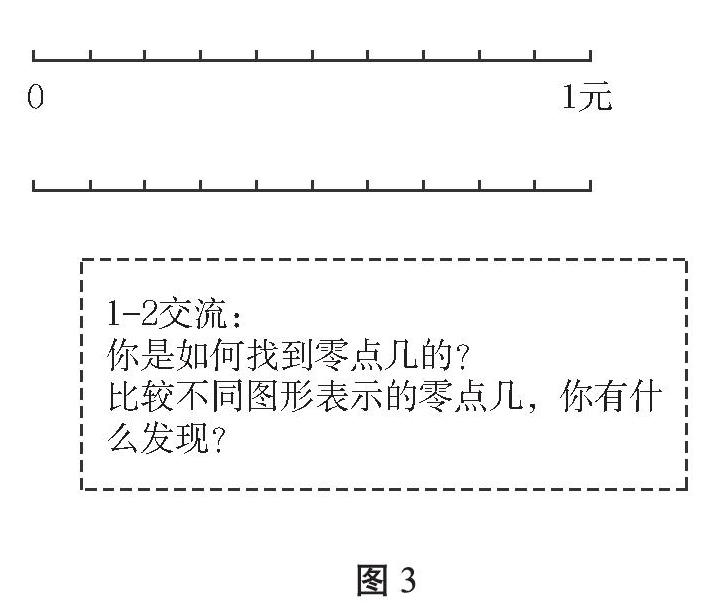
評價1-2（見圖3）的小目標是：經歷小數（零點幾）含義的探究過程，理解十分之幾就是零點幾。學生已經認識十分之幾元是零點幾元，但去除情境，要達成目標十分之幾就是零點幾，需要大量認知的積累，才能由量變轉為質變。于是創設評價1-2 ：選擇下面一個圖形，你還能找到零點幾？在不同的情境里找小數，拓展對小數意義的整體認知。大部分學生都能夠解決“1元”情境圖，有能力的學生可以挑戰“1米、1千克”的情境圖。這樣可學的材料，目的是讓不同層次學生有不同發展，不同層次學生都能介入學習。

（2）基于核心問題二：認識幾點幾的評價創設

評價2-2（見圖4）的小目標是：理解十分之幾就是零點幾，利用小數的含義，解決生活中的數學問題。教材出現的小數比較小，可能會導致學生誤認為小數比整數小。創設評價2-2在2008年北京奧運會射擊項目上，烏克蘭選手蘇霍魯科夫以總成績1272.4環獲得銀牌，我國射擊運動員邱健總成績1272.5環，以0.1環優勢獲得金牌。這樣的創設，既解決生活中的小數問題，也使學生對小數有了新的認識。

二、經歷“可見的思維”，讓不同層次的學生探究留痕

1.在新知探究中經歷可見的思維

（1）核心問題一：認識零點幾的思維經歷

通過圖1任務1-1交流小貼士“你是怎么表示出0.6元的？”，學生呈現出不同思維水平。水平一：選擇6個1角表示0.6元。0.6元就是6角。水平二：畫出一部分表示0.6元，或在圖形里只畫出6小份表示0.6元。水平三：先平均分成十份，再涂出6份表示0.6元。0.6元就是元。“水平三”體現了平均分的意識，也溝通了分數與小數的聯系。雖然大家都能介入學習，但不同層次學生在探究中留痕不一樣。不同水平的學生在交流中，逐層展示不同的思維表征，促進了思維的提升。

（2）核心問題二：認識幾點幾的思維經歷

通過圖2任務2-1交流中的“說一說：你是怎么找出小數的？”學生呈現出不同認知。認知一：1～2之間平均分成十份，十分之二就是0.2。認知二：0.2不對，因為1～2之間的數應該是一點幾，2～3之間的數是二點幾。比1多0.2就是1.2，比2多0.9就是2.9。認知三：比3少0.1就是2.9。認知一雖然是錯的，但卻是學生自主思考，作為課堂生成，讓學生在對話中厘清0.2與1.2的不同，不同思維水平的碰撞，既夯實了對1.2的理解，又實現了對0.2與1.2的區別的理解。同時，由零點幾到對幾點幾的認識，對學生而言，也是一種思維上的突破，是一種再學習、再研究、再創造。通過任務2-1交流“將數軸上的數分分類，說說分類的理由。”，學生呈現出不同認知。認知一：將小數分三類，零點幾、一點幾、二點幾，或將小數分兩類，小于1、大于1。認知二：分為自然數和小數兩類，0、1、2、3是自然數，也是整數，0.6，1.2，2.9是小數。通過認知一的學習，學生可以很巧妙地認識、介紹小數各部分名稱：小數含有整數部分和小數部分。認知二，借助于學生的作品，巧妙的板書，數可以有整數和小數，結構化學習，讓學生整體建構小數的認識。最后，在交流任務2-1中的想一想“如果1表示1元或1米，方框里的數各表示多少？”，讓數學知識回歸生活，使學生會解釋具體情境下小數含義。任務2-1的設計，學生在研究中呈現多樣化思維留痕。

2.在評價學習中經歷可見的思維

（1）評價1-2的思維經歷

通過圖3評價1-2交流小貼士“你是如何找到零點幾的？”，學生呈現出不同思維認知。認知一：十分之幾元就是零點幾元;十分之幾米是零點幾米;十分之幾千克是零點幾千克。認知二：單位不同，都有0.1～0.9九個小數。認知三：十分之幾就是零點幾。

（2）評價2-2的思維經歷

通過圖4評價2-2交流小貼士“射擊的成績你是怎么想的？”，學生呈現出不同認知。認知一：比8環大，8.4環;認知二：比9環大，比10環小，應該是9點幾環。認知三：比9.5環小，所以是9.4環。不同層次思維的交流、碰撞，又讓所有同學的思維得到互補性發展。

三、發現“可現的生長”，讓不同層次的學生知識增長

1.新知探究中的知識增長

通過圖1任務1-1交流小貼士“比較不同圖形表示的0.6元，你有什么發現？”，一次探究，多次交流。從6角就是0.6元，再進階到階段性目標：十分之六元就是零點六元。學生思維得以進階，知識得以增長。通過圖2任務2-1的創設，達到階段目標，由零點幾突破到對幾點幾的認識，數軸的上方是小數，下方是整數，較好地整體構建了小數的認知。

2.評價學習中的知識生長

通過圖3評價1-2交流小貼士“比較不同圖形表示的零點幾，你有什么發現？”，引導學生了解階段目標“十分之幾就是零點幾”，學生們的思維在留痕、碰撞中不斷發展。通過圖4評價2-2交流小貼士：你對小數有什么認識？學生發現：小數很精確，整數不能解決的時候，可以用到小數。1272.4也是小數，發現小數并不小，使學生對小數的認知得以拓展。

對于轉型后設計的教學建議，探索基于“學”的教學設計轉型要關注五個前提，三條路徑，三個目標。每個任務創設要圍繞“核心問題、任務目標、基于教材、基于學生、任務目標”五個前提，要綜合考量分析五個方面，并進行融合，形成任務。同時，通過創設“可學的材料”、經歷“可見的思維”、發現“可現的生長”，形成可學、可見、可現的任務路徑。最后還要考慮三個達成目標：讓不同層次學生學習介入、讓不同層次學生探究留痕、讓不同層次學生的知識儲備得到增長。

總之，轉型后任務設計要讓不同層次的學生都能介入，讓“學”的痕跡留得下，讓學生的思維看得見。