最速降線問題的歷史與一種巧解

楊亦逸

(上海交通大學科學史與科學文化研究院 上海 200240)

1 引言

最速降線問題在數學史上是因約翰·伯努利(Johann Bernoulli，1667-1748)向全歐洲的數學家們發出挑戰而聞名于世的.在1696年6月的《教師學報》(Acta Eruditorum)上，他以“新問題——向數學家們征解”為題，將問題表述成如下敘述：

“給定垂直面上的兩個點A和B，一個質點M受重力作用，從A點開始，在最短的時間內到達B點，曲線AMB會是怎樣的？”[1]

他稱這條曲線為“最速降線”(拉丁轉寫brachistochrone，源自于希臘語βρàχιστο?χρòνο?)，由希臘語中的“最短”和“時間”兩個詞合成而來；拉丁語“brachisto”的含義是最短的，“chronos”的含義為時間，因此這一問題字面意義應為求“最短時間”問題.最速降線問題的特殊性在于，它與之前運用微積分分析求極大值和極小值的問題大異其趣，而是需要求出一個滿足條件的函數(即曲線的方程)，這是微積分出現以來還未涉足的領域.約翰自己也在公布解法的信中如是說道：

“到現在為止，已經出現了許多處理最大值和最小值的方法，但似乎與此主題之間沒有什么微妙的聯系，以至于無法被他們的洞察力所參透……即使是那些知名人物，如笛卡爾、費馬等，也一定會坦率地承認，他們的權威方法在這里是不充分的……在他們的著作中，我們沒有發現對這種類型的極大值和極小值問題的考量，他們并沒有將方法普遍化地運用.”[2]

由此觀之，約翰敏銳的數學嗅覺使他敏銳地觸及了這一問題更深層次的意涵：新的問題需要有新的、普遍的方法來解決，過去的方法已然不適用，那么對它的研究很可能促成新的數學理論的形成.事實上，最速降線問題的確引發了其后變分學的發生，以及更為廣泛的泛函分析和數學物理方法研究.

2 問題溯源 伽利略的初步探索

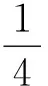
而在伽利略1638年的《關于兩門新科學的對話》(Discorsi e dimostrazioni matematiche intorno a due nuove scienze)中，他進一步對此問題的回答進行了總結：“從前面可以推斷，從一個點到另一個點的最快下降路徑不是最短的路徑，即一條直線，而是一個圓弧.……因此，內接多邊形越接近一個圓圈，從A下降到C所需的時間越短.對于小象限，已證明的象限也適用,推理是一樣的.”[4]

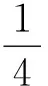
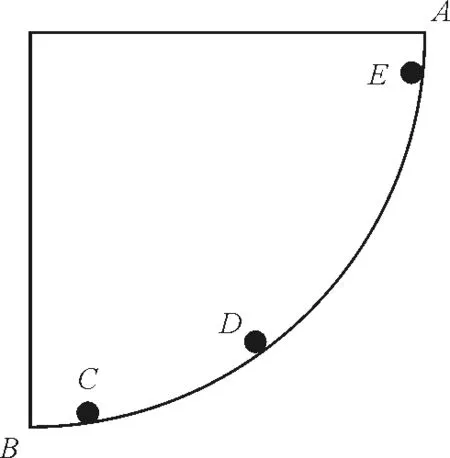
圖1 《兩種體系》原圖

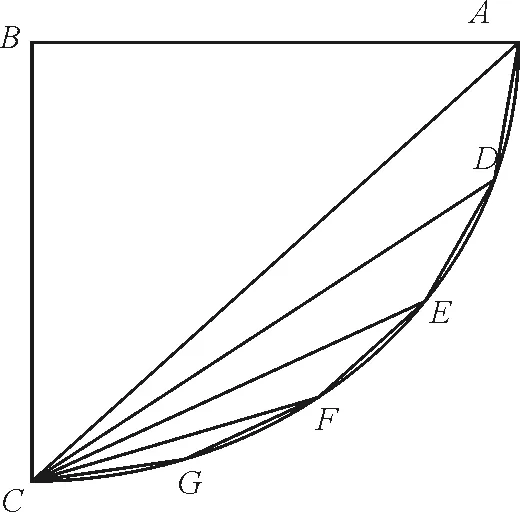
圖2 《兩門科學》原圖

伽利略所作推論的邏輯鏈條在最后一步產生了錯誤，結論流于草率，而且有預設答案的嫌疑.伽利略是深受古希臘以來的天文學傳統影響的，他所支持的哥白尼學說是建立在天體以圓為完美的運行軌道的基礎上的；而且在知曉了開普勒的工作之后，他仍然堅持這一點.這就可以解釋他偏愛圓或圓弧作為運動路徑的答案，因為任何完美的運動都應當與圓周運動相關.

近期，水利部印發《關于切實加快重點水利項目建設進度的通知》，要求各地切實落實加快重點水利項目建設各項責任，著力解決影響水利項目建設進度的關鍵問題，加快2012年重點項目建設進度，如期、優質、高效完成年度水利建設任務。

此外，疏于實證而停留在思想實驗層面，也是導致伽利略產生錯誤結論的原因之一.在確認了直線段和折線段不可能成為用時最少的路徑后，伽利略直接就認為平滑的圓弧曲線就是答案，“顯然，他把自己的比較范圍鎖定在直邊形、圓弧這樣一些‘規則’的圖形之中，如果要得到正確的結論，還需要將比較的對象進行擴大，也就是需要在更大的曲線范圍內考慮問題.從現在的觀點看，至少應當把最速降線問題的解——旋輪線弧包含在內.”[5]伽利略很可能并未設計并制造數個斜曲面，以實驗方式來比較物體在其上的運動時間；同時，他也缺乏對除了圓錐曲線外其他類型曲線的認識.

伽利略無法得出正確解還有數學方法上的因素.在他的兩大著作中，廣泛使用的是自幾何原本以來就被確立為傳統的幾何方法，而幾何方法中的窮竭思想導致的錯誤判斷是很常見的，從阿基米德到他同時代的開普勒，都有過對窮竭類比方法的錯誤應用.最速降線問題的解決正是得益于數學思想方法的變革：微積分的產生以及解析幾何代數分析的方法，成為了解決這一問題的有力工具.正如約翰·伯努利后來評價的那樣[6]：

“盡管伽利略毫無疑問是他同時代最具洞察力的人物，然而由于缺乏新的分析工具，才使得這樣一位偉人做出了懸鏈線是一條拋物線、最速降線是一段圓弧此類錯誤猜測.”

3 公開挑戰的過程

在發起公開挑戰的同時，約翰在同年6月9日寫信給他的老師，同時也是《教師學報》主編的萊布尼茨，私下告知其這一問題.一周之后的6月16日，萊布尼茨回信簡要地給出了一種解答[7]，但他建議約翰將挑戰截止時間由1696年底延至1697年復活節，使得歐洲其他地區的一些數學家，特別是法國和意大利的數學家，能擁有充足的時間準備和參與這次挑戰.在沒有收到任何回信解答后，約翰·伯努利于1697年元旦發表了有關此問題的又一次公告.公告中他聽從萊布尼茨的建議，將原來所設的挑戰終止期限推遲至當年復活節.

這一次，在規定的時間內，共有4位數學家給出了解答：牛頓、雅各布·伯努利(Jakob Bernouli，1654-1705)、萊布尼茨和洛必達(Guillaume de l′Hpital，1661-1704)，解答方案發表在了當年5月的《教師學報》上[8].值得一提的是牛頓早在1697年1月29日花費一個晚上就得出了解答，牛頓的心態可以從他的話中窺得一二：“我不愿意在有關數學的事情上被外國人糾纏和嘲弄……”.牛頓的解答匿名發表在了當月的《哲學匯刊》(Philosophical Transactions of the Royal Society of London)上[9]，而據說約翰在見到這種解法后，驚呼“從這鋒利的爪中，我認出了雄獅”.

像這樣廣而告之的大型挑戰，其實質固然是數學本身的進步導致的，因為沒有這些新問題、新方法和新思想，即使數學家們再如何爭強好勝，也不能無事而生非.因此,最速降線問題的新穎性、重要性和奇特性是引發此次挑戰的重要內在誘導因素[5].對新發現秘而不宣卻采取公開挑戰的形式，則是由于公開挑戰的文化傳統、英國與歐陸的分離主義情緒、以及幾位主要參與者的性格特點等幾點外因所致.

公開挑戰的傳統早已有之.16世紀在意大利發生的塔塔利亞(Tartaglia, 1499-1557)與菲奧爾關于一元三次方程的競賽，以及其后卡爾達諾(Girolamo Cardano, 1501-1576)弟子費拉里(Ferrari Lodovic, 1522-1565)和塔塔利亞(NiccoloTartaglia of Brescia, 1499-1557)關于解一元三次、四次方程的公開比賽是代數發展史上濃墨重彩的一筆，塔塔利亞更是飽嘗了勝利帶來的喜悅和榮耀以及失敗結下的苦果.對自己的成果秘而不宣，既是限制于當時并不便利的傳播條件，也根源于沒有成熟完整的學術評價體系和社會建制；公開挑戰則是在此情形下為保障發現的優先權和獲取學術資本與聲譽的應對之策.

最速降線的挑戰適逢英國光榮革命之后，英國的代議制政體確立，與此同時英國人也扭轉了英荷戰爭失敗所帶來的海上貿易局面.政治和經濟上的變化促使著英國人心態的轉變，上文所引牛頓的話可見一斑.這種分離主義的情緒可以從其后的微積分發明權之爭中窺見一斑：1699年法蒂(Nicolas Fatio de Dullier, 1664-1753)發表了宣稱牛頓在微積分的發現中處于優先地位、并且很大程度上暗示萊布尼茨從他那里竊取了一些想法的文章[10]，由此開啟了英國與歐陸學者曠日持久的爭論，直到1716年萊布尼茨去世才稍為平息.因此，國家層面的實力對比變化也有部分影響.

約翰·伯努利個人的好勝心則是發起此次挑戰的直接原因.雅各布是約翰的長兄，也極富數學上的才華，兩人在學術上多有爭論，不止在最速降線問題上，還在懸鏈線挑戰以及教職等多方面有矛盾；兩人既是兄弟，又是對手.而約翰發起挑戰的目標還不止于此，他的老師萊布尼茨，以及當時已任皇家鑄幣局總監的牛頓，都被他視作了潛在的挑戰對象.約翰在他的挑戰書中這樣寫道：

然而牛頓也不示弱，在造幣局公務繁忙之余仍輕松應對了挑戰.總之，約翰和牛頓的好勝心其目的都是求真的，是對數學問題本身的關注.

約翰·伯努利如此踴躍發起挑戰的原因，還有一部分來源于他本人對于其解法的自信；他的解法巧妙地運用了斯涅爾折射定律和費馬原理，將質點的運動與光在非均勻介質中的連續折射進行了類比，找到了最速降線問題的一種巧妙解答.

4 約翰·伯努利的巧妙解答

當光以斯涅爾定律進行折射時，有

(1)

即曲線上每一點(除了起點外)的切線和垂直直線夾角(即入射角)的正弦值與光在該點處的速度成正比.

如圖3所示，A為光運行的起點，FAG為水平線，AD為豎直線，FGD側為折射率不同的介質，如HM線上的介質密度處處相同，以AC為x，AG為y，則在微分三角形Mmn中，有

(2)

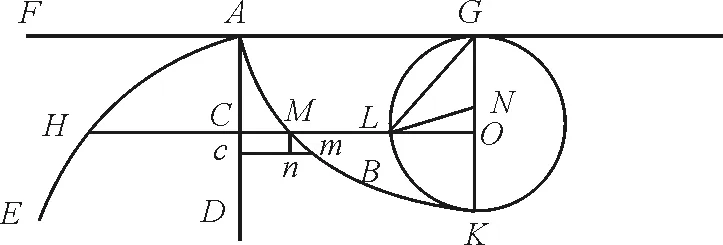
圖3 約翰的證明示意圖

(3)

其中a為比例因子，v為待求曲線上一點的速度.而弧微分dz2=dx2+dy2，則

整理可得

于是有

(4)

再根據伽利略時代起就已知的質點下落的速度與高度的平方根成正比的規律，則圖3左側曲線AHE為拋物線，CH即為此時的速度v，此時可設

將此代入式(4)，則有

(5)

而式(5)正是擺線(cycloid，又叫旋輪線)的微分方程，表示直徑為a的圓產生的倒擺線,即如圖4所示的下凸曲線.

圖4 最速降線示意圖

約翰在得到答案后表示了由衷的驚奇和贊嘆，因為最速降線正是當時數學家們所熟知的擺線，也正是伽利略為它命名的：

“在作總結之前，我不能不再次表示我對惠更斯(Christiaan Huyghens, 1629-1695)的等時曲線(tautocbrone)和我們的最速降線碰巧相同所感到的驚奇.此外，我認為值得注意的是，這種同一性只能在伽利略的假設中找到，因此從這個假設中，我們也可以推測，大自然希望它是如此的.因為大自然總是習慣于以最簡單的方式運作，所以在此她通過同一條曲線完成兩種不同的任務.”[2]

約翰在他自己巧妙的解答中讀出了大自然的經濟本性：大自然總是會做效率最高的事情.費馬原理中已經含有了這種自然是最經濟化的思想.這一思想使得約翰不再像通常使用微積分求極大值極小值那樣很局部地考察粒子在每個點上的情況，而是考慮所有可能的路徑并且找到大自然選擇的最好的那一條.而且拋開這些自然神論的宗教觀點不談，只將最小光程的光傳播現象當做一個經驗事實也足以使人接受.約翰的這種解法雖然沒有直接運用變分法的思想，但最小時間的思想在其解法中起了基礎性的作用，具有極為重要的先導意義；約翰的這項工作也在很大程度上引發了歐拉、拉普拉斯關于力學中最小作用原理的研究，進而為變分法的創立和發展提供了強有力的動力[5].

附言

最速降線問題完備的解答需要用到變分學的知識，當時以及后來的數學物理學家都給出了許多各具特色的解法，促進了18世紀數學和物理的發展.

擺線(即最速降線)在工業中的應用十分廣泛，那么在生活中呢？譬如圖5所示的滑板場，如果設計成擺線形狀，就可以成為下滑最快的坡道.但是很遺憾，設計者們雖然知道這一點，但從不設計成最速降線.

圖5 滑板場