基于文化基因算法的機組排班問題研究

◆陳肯 張廣偉

（中國民用航空飛行學院空中交通管理學院 四川 618300）

機組排班是根據航班計劃和機型屬性等要求，為航班指派相應的機組人員（包括機長、副駕駛、機械員、領航員、通信員等）并實施航班飛行任務的過程[1]。機組排班問題主要分為任務環生成（Crew pairing problem，CPP）和機組人員指派（Crew assignment problem，CAP)。CPP 問題主要是任務的生成，發現一組往返飛行航線并且覆蓋所有的航班。CAP 問題是任務的分配，主要是將已分割完成的任務派遣給各組機組人員執行[2]。本文的研究主要針對機組排班中最核心的問題任務環生成（CPP）問題。

Budi Santosa[3]提出了一種基于遺傳算法的簡單迭代變異(SIMA)方法來解決航空公司機組排班問題。在排班的質量與時間上均取得較好結果。Frédéric Quesnel[4]提出了一種啟發式分支定價算法解決了帶有語言限制的機組排班問題。張米[5]系統分析提出了機組排班問題模型并考慮了延誤因素，運用列生成算法計算，取得了較好的優化結果。

本文提出了一種基于動態文化基因算法的中型航空公司任務環配對問題的求解方法。目標是找到成本最低的機組人員配對。

1 文化基因算法

機組排班問題是典型的NP_hard 問題，受系統復雜性和多種約束條件的限制[6], 求解非常困難，常用算法有分支定價算法、分支切割算法、列生成算法以及遺傳算法等啟發式算法。其中遺傳算法是求解機組排班問題的經典算法，有著相對成熟的理論體系。本文選用遺傳算法的改進算法文化基因算法進行求解，遺傳算法已被大量運用于此問題的研究中并證實效果顯著[7]。但標準遺傳算法會過早向目標函數的局部最優解收斂且算法對初始種群的選擇具有一定的依賴性[8]。而文化基因算法是一種基于種群的全局搜索和基于個體的局部啟發式搜索的結合算法。

文化基因算法是一種框架,可以采用不同的搜索策略可以構成不同的文化基因算法,如全局搜索策略可以采用遺傳算法、進化規劃等,局部搜索策略可以采用爬山搜索、貪婪算法、禁忌搜索等[9]。這種局部與全局的混合搜索機制可以在某些問題領域比傳統遺傳算法快幾個數量級。文化基因算法基本框架如圖1所示。

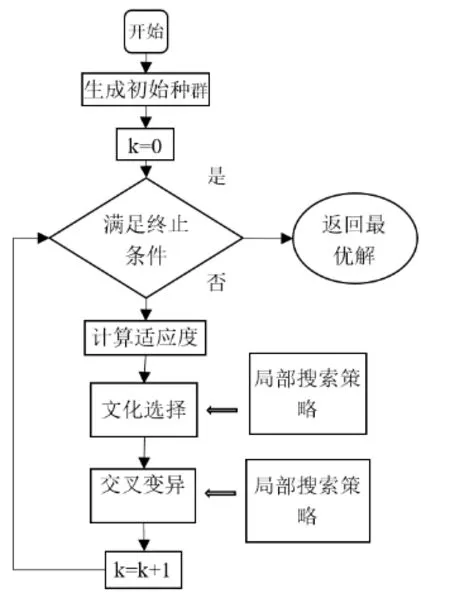
圖1 文化基因算法框架圖

2 問題模型

2.1 航空公司排班基本原則和約束

在機組排班過程的任務環生成階段，依據中國民航局制定的飛行運行手冊和各民航公司內部制定的排班規則[10]，來組合任務環。包括飛行時間限制、值勤時間限制、航段個數限制、人員搭配限制以及機組資源本身的限制。現將主要規則整理如表1所示：

表1 限制條件匯總

2.2 數學模型

通過分析國內外機組排班流程算法的特點、我國民航局及航空公司的相關規定,構建了機組排班問題的數學模型

式中cp代表任務環p的成本，包含機組的飛行津貼，撘機機組成本以及在外過夜成本[5]。xp是決策變量，0 代表任務環未被選中，1代表任務環被選中。afp=1 表示p任務環中包含i航班，否則afp=0。

式（1）目標函數為最小化總任務環成本。式（2）確保每個航班至少被覆蓋一次。式（3）限制了決策變量的可行域。

3 用深度搜索算法生成飛行任務環池（pairsALL）

本文利用啟發式算法來產生初始機組任務，事先考慮航班連接時的限制條件，在航班連接時避免了窮舉算法所有可能的無效率性，在處理實際問題時，可快速產生可行初始機組任務。

3.1 構建航班網絡

構建航班聯接的網絡圖時，需要考慮的因素包括航班聯接的物理地點約束與時間約束。前導航班與后續航班的起降時間滿足最短、最大轉換飛機時間約束，最短休息時間約束且前機的降落機場為后機的起飛機場本文便稱這兩個航班之間存在合法連接。對每個航班建立航班樹（圖2），運用c++的鏈表結構進行編程，在以后碰到求航班的后續可行航班只要根據網絡查找下一個航班的航班樹，這樣可以減少計算量。本文構建的航班連接的網絡圖示例如下：

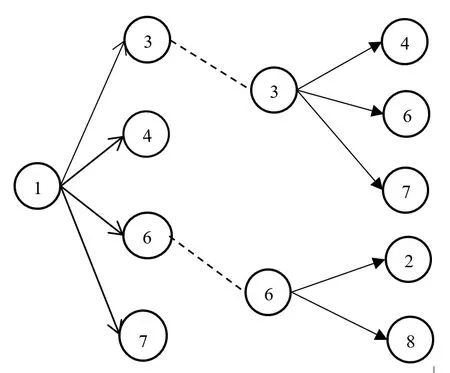
圖2 航班網絡圖

1）節點。節點代表不同的航班。每個節點包含有航班的起止機場與時間信息。

2）連接線。每根連接線都代表節點與節點之間的合法連接，需要滿足包括時間、地點的約束等等。

如圖所示，圖中有三個航班樹，航班樹相連構成航班網絡，航班1 的合法連接航班有3、4、5、6，航班3 的合法連接航班為4、6、7，航班6 的合法連接航班為2、8。在搜尋過程中，可以由航班1 的航班樹定位到航班6 的航班樹，可形成1、6、2 和1、6、8 兩個合法任務環，其余同理。

3.2 根據生成的勤務組組成飛行任務環池

任務環生成方法是一個遞歸的過程，借助3.1 提出的航班網絡，采用遞歸的方式進行搜索。在第一階段，所有的航班都按照主要程序進行審查。對于從基地開始的任務，將執行搜索算法進行遞歸，可以將符合條件的任務環加入到主集中。需要滿足的約束有：

時間約束：在外過夜不超過3 天，即同一個任務環最多包含4天的勤務

地點約束：下一個勤務起始的機場需要是上一個勤務終止的機場。

算法一：生成所有任務環

4 選擇初始子集（pairsActive）

本文利用啟發式算法生成一個隨機任務環子集（從主集中選擇），這個子集中包含的任務環可以覆蓋所有航班，并不要求初始子集為最優子集，只需保證可行性，在后續會通過啟發式算法對子集進行更新優化。下面開發了一種啟發式算法來生成初始子集。偽代碼如下：

1 對每一個航班在任務環總集（pairAll）中搜索包含該航班的任務環加入到子集中（pairsActive）。

2 在航班集合中尋找下一個未被覆蓋航班。

3 重復1 步驟，直到所有航班均被覆蓋。

上述三小節是為了產生成用于生成染色體的任務環子集（pairsActive），該集合任務環將作為遺傳算法的解空間。該集合越大，迭代選取到最優組合的概率越大，但會增加算法無效的計算量，選取合適數量的子集有助于減少迭代到最優的次數。

5 文化基因算法

5.1 基因編碼

本文基因編碼采用01 編碼，每一個染色體位代表任務環總體中相對應的任務環是否被選中，0 代表任務環未被選入，1 代表該任務環被選入。

5.2 生成初始種群

初始種群是文化基因算法的第一階段。這個群體中的每一條染色體都代表了該問題的一個可行解決方案。本文開發了一種啟發式方法覆蓋每一次飛行任務，生成一個可行的初始種群。

算法二：初始化種群

5.3 適應度

適應度采用最小化成本

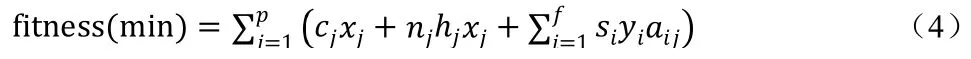
式中cj代表任務環j的成本，包含飛行固有成本加機組責任時間成本。nj代表任務環j 包含的過夜次數，hj代表旅店成本，xj表示任務環是否包含在該染色體中，0 表示未包含，1 表示被包含。si代表單次航班i的花費，yi表示i航班是否為撘機航班，若是則為1，不是則為0。aij表示航班i是否被任務環配f 包含，若是，則為1，否則為0。

5.4 選擇算子

采用二元錦標賽選擇法，在錦標賽選擇法中，從種群中隨機挑選兩個個體，然后將適應度最優的個體選出進入下一代。這個過程重復進行直到子代種群數量達到規定數量。

5.5 交叉算子

在選擇祖先(母親和父親)染色體產生新的孩子后，可以利用交叉算子可以有助于將優良個體的染色體片段遺傳給后代,同時交叉算子一般起全局搜索的作用,可以開采未知的空間。本文采用單點遺傳方法。

（1）先產生隨機數確定交位點；

（2）交叉位點后的基因實現單點交換；

（3）交叉完成。

5.6 突變算子

采用位翻轉變異算子保證算法不捕捉局部最大值和局部最小值點。設置突變概率為0.2。

（1）隨機確定突變點位；

（2）突變點位的值由0 變1，或由1 變0。

5.7 啟發式修補算法

經過遺傳交叉變異后的個體可能無法滿足航班約束（每一航班至少被覆蓋一次），所以需要設計一種啟發式算法修復子代染色體，使之滿足航班約束。本文設計了一種任務環選擇指標，保證成本較低的任務環進入到解集中。

任務環選擇指標=任務環P 的成本/集合中未被覆蓋的航班數量，偽代碼如下：

（1）遍歷染色體，搜索未被覆蓋航班；

（2）在子集（pairActive）中搜尋包含該航班的任務環；

（3）選擇任務環選擇指標最小的任務環加入染色體中。

5.8 局部啟發式搜索算法

局部啟發式搜索算法是文化基因算法的一個重要特征，用局部啟發式搜索可以模擬由大量專業知識支撐的變異過程,以使解決算法更有效率。這一過程目的減少無用的任務任務環，確保了染色體的適應度優化的同時保證滿足航班約束。偽代碼如下：

算法四：局部搜索算法

（1）選擇染色體解集中的任務環，將該任務環從染色體中移除；

（2）若解集中航班覆蓋約束不被滿足（不是所有航班都被覆蓋），則將該航班重新加入；

（3）重復上述兩步，直到遍歷所有解集中的任務環。

5.9 種群替代策略

文化基因算法的最后一步是種群置換。在這一步，父代和子代的染色體需要通過一種選擇策略確保種群數量的固定。因為種群的數量是固定的，所以種群替代策略可以確保種群的數量保持不變。種群更替階段使用的兩種主要方法是世代法和穩態法。本研究采用穩態方法。在這種方法中，在每次迭代中生成一個或兩個子代。然后，這個后代的染色體取代了種群中最差的個體。

6 文化基因算法偽代碼

文化基因算法偽代碼如下：

（1）對每個個體計算適應度

（2）while 終止標準不滿足do

（3）Parent1 ←Select-Parent(population,tour-size)

Parent2 ←Select-Parent(population,tour-size)//應用錦標賽算法選擇父代

（4）Child1 ← Apply-Crossover(one-point ceossover, Parent1,Parent2)

Child2 ←Apply-Crossover(one-point ceossover,Parent1,Parent2)

（5）Child1′←Apply-Mutation(bit-flip random,Child1)

Child2′←Apply-Mutation(bit-flip random,Child2)//進化算子

（6）Child1′←局部搜索(lc,Child1′),Child2′←局部搜索(lc,Child2′)

（7）將種群中最差的兩個個體替換為父代和子代中最好的兩個//種群替代；

end while

7 優化方案和實現部分

通過c++語言，在visual studio 平臺上進行程序編寫。設置迭代次數為1800 次,每迭代100 進行一次更新搜索空間算法。錦標賽選擇法行程為2，交叉概率為0.9，突變概率為0.2，設置種群規模為20。機組飛行小時津貼為400 元/小時，每個機組的任務津貼為1000 元/天，機組在外過夜的旅館成本為500 元/天。航班加機組成本，每個航段的成本是不相同的，這里為了研究方便，假設加機組成本都是一個固定值500/小時[13]。選用國內某中型航空公司一周的航班數據，分別用Kornilakis 所提遺傳算法[14],更新解空間的遺傳算法與本文所提算法進行實驗（表2所示分別用算法一二表示）。該公司一周共有航班549 架次，通過深度搜索算法產生了1683 個勤務組和79862 個任務環。實驗結果如下：

表2 對照實驗算法

表3 對其他作者開發的遺傳算法和本文所提算法進行的測試結果。在兩項實驗中分別對最優解的在外過夜次數，撘機次數，撘機總時間總花費（元）等關鍵績效指標進行了統計。在評估解決方案的優劣時需要參考的三個重要參數為執勤總時間、撘機總時間和在外過夜次數。比較遺傳算法，所提的更新搜索空間策略能有效縮減解空間大小，且在減少撘機次數和過夜次數方面有顯著效果。對比遺傳算法與所提算法可以看出，局部搜索策略能夠起到小幅優化效果。通過對這三個重要參數的比較且同時參考比較三種種算法的其他KPIs 表明，本文所提出的算法比之前的研究產生了更好的結果，該算法具有良好的性能。

表3 機組排班實驗數據

表4 列出了三個重要的參數：執勤總時間、撘機總時間和在外過夜次數在迭代過程中的優化趨勢。在600到800次迭代之后趨于收斂。

表4 所提算法不同迭代次數的最優解KPIs

圖4 為兩種算法的適應度變化曲線，可以看出本文所提算法在解決機組排班問題上具有更優的性能。

圖4 適應度變化曲線圖

8 結束語

針對航空公司機組人員配對問題，本文提出了一種基于動態文化基因算法的改進算法。由于機組任務環配對是排班過程中成本識別的主要環節，如何降低機組成本、增加機組效用、實現最優機組配對具有重要意義。所以本文的優化從關鍵績效指標(KPIs)，如撘機時間、勤務天數和在外過夜次數等與機組任務環優化相關的成本指標著手，提出了基于動態文化基因算法的改進算法。實驗結果顯示，與現有方法相比，本文所提出的算法生成了更優解。所提出的更新搜索空間的算法對減少撘機時間和減少過夜停留次數有顯著效果。

本研究的主要貢獻如下：

第一項貢獻是利用動態遺傳算法和每次迭代的染色體長度變化來解決任務環配對問題。該算法基于文化進化理論，采用全局搜索與局部搜索相結合，有效加快了基因進化的速度。

第二項貢獻是利用深度優先搜索算法結合航班網絡設計了用于快速生成可行任務環的啟發式算法。經試驗該算法可生成大量可行的任務環。

綜合考量來看，本模型綜合考慮了機組人員撘機次數、過夜次數、機組人員的成本等問題，解決了傳統排班方法無法給出的算法模型，為航空公司機組排班算法的進一步研究提供了良好的理論依據，對實際應用提供了較好的參考。