考慮盾殼與土體摩擦力的盾構下穿既有地鐵隧道施工控制研究

來弘鵬，王騰騰，張林杰，袁 野，羅 維

(1.長安大學公路學院，陜西 西安 710064；2.中鐵北京工程局集團有限公司，北京 102308)

0 引言

隨著城市的發展，地下工程數量日益增多，新建隧道穿越已建隧道的工程也越來越多。盾構下穿施工過程中，不可避免對地層及既有隧道產生擾動，引起隧道結構的變形。因此，確保盾構施工時既有結構穩定、保障地鐵正常運營已成為研究熱點。

針對此，國內外眾多學者從理論分析、數值模擬、模型試驗等方面進行研究，取得了相應的成果。例如：Yin等[1]以深圳地鐵9號線下穿4號線隧道為例，研究了EPB盾構盾尾空隙對既有建筑物沉降的影響，并利用三維有限元法分析了MJS工法的作用；Lin等[2]基于長沙地鐵某工程，利用數值模擬研究了新建雙線隧道斜下穿時既有隧道的變形、內力特性，分析了盾構隧道施工對地表沉降槽的影響；Li等[3]采用自動高性能全站儀系統連續監測了深圳地鐵蛇口線雙跨隧道在不同下穿階段的位移以及襯砌性能；Jin等[4]基于深圳地鐵下穿施工實例的大量監測數據，分析了新建盾構隧道下穿時既有隧道及地表的變形和襯砌應力，研究了既有隧道沉降的影響因素，并提出了一種預測既有隧道沉降的經驗公式；張瓊方等[5]以杭州地鐵4號線近距離下穿既有地鐵1號線為研究對象，對盾構施工參數、既有地鐵變形進行監測，提出了保證既有隧道安全的施工措施；張冬梅等[6]基于Kerr 地基梁理論，建立了新建隧道施工對上方已建隧道影響的解析分析方法；魏綱等[7]基于 Mindlin 位移解和隨機介質理論，考慮正面附加推力、盾殼與土體之間的摩擦力、附加注漿壓力和土體損失，研究了類矩形盾構施工引起的土體豎向位移及各因素的影響；張治國等[8]基于鏡像法與 Winker 地基模型，提出了類矩形盾構隧道施工誘發鄰近管線變形的簡化計算方法；來弘鵬等[9]以西安地鐵1號線二期下穿既有1號線出入段線為依托，通過現場調研、數值模擬和現場監測等方法研究了施工參數對既有隧道軌道高差的沉降影響規律；林志軍[10]以長沙地鐵3號線盾構隧道下穿武廣高速鐵路瀏陽河隧道工程為依托，采用理論分析、數值計算等方法對盾構下穿施工過程中既有高鐵隧道響應規律進行了研究。

綜上所述，關于盾構施工的數值模擬工作已取得較大進展。如文獻[11-14]在模型中考慮了盾構土艙壓力、注漿壓力、漿液硬化的影響；文獻[15]在計算中考慮了等代層與盾尾空隙的關系；文獻[16]則提出了一種考慮地層損失率的動態調控方法。但目前關于盾構下穿的計算模型大多進行了簡化，鮮有考慮盾殼與周圍土體摩擦力的實際分布對計算結果的影響，而摩擦力又是盾構掘進引起既有隧道附加應力變化、水平及豎向位移的重要因素[17-19]；另外，在黃土地區盾構下穿過程中土艙壓力、摩擦力、注漿壓力等施工參數對既有隧道結構變形的影響尚不完善。

鑒于此，本文綜合考慮盾構自重、盾構四周土壓力實際分布特征，推導盾構掘進中盾殼與土體摩擦力計算公式，并采用FLAC 3D有限差分軟件的Fish語言，模擬盾構下穿施工流程；依托西安地鐵5號線新建盾構隧道近距離下穿已建2號線的工程實際，設計接近區、穿越區和脫離區3個區段施工參數調整方案；研究盾構下穿過程中既有隧道左右線豎向位移和橫向水平位移規律、各施工參數對結構變形的影響機制，最終將模擬結果與現場實測數據對比，以驗證研究成果的合理性。

1 工程概況

既有西安地鐵2號線埋深9.4 m，為標準馬蹄形斷面，斷面寬度6.3 m，高6.6 m，初期支護厚25 cm，二次襯砌厚30 cm；西安地鐵5號線南稍門—文藝路盾構區間隧道左、右線將橫向垂直下穿2號線南稍門站前區間隧道，下穿凈距2.5～2.6 m，埋深18.5 m，其平面圖和剖面圖分別見圖1和圖2。

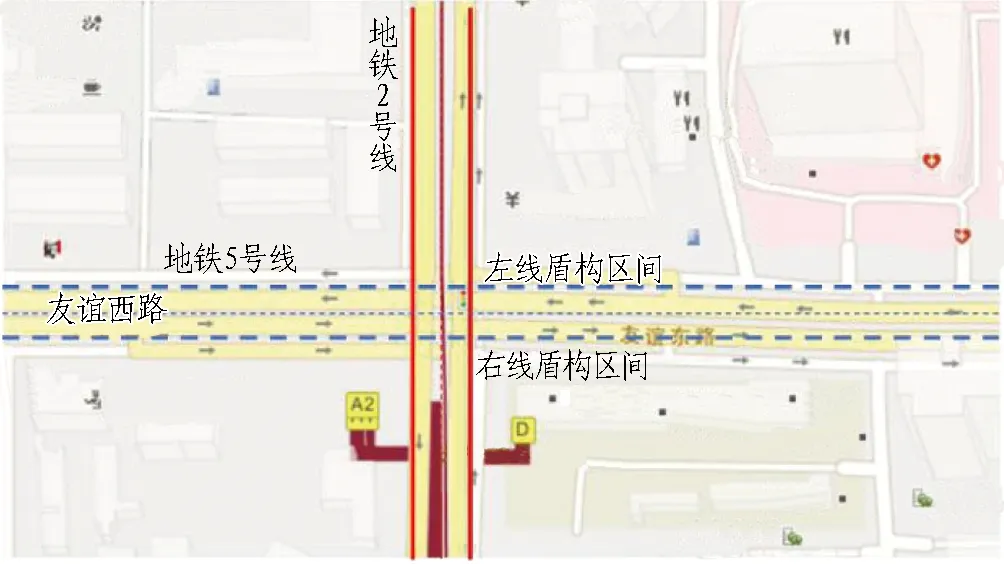
圖1 西安地鐵5號線下穿既有2號線平面圖Fig.1 Plan view showing Xi′an metro line No.5 crossing underneath line No.2

圖2 西安地鐵5號線下穿既有2號線剖面圖(單位:m)Fig.2 Profile showing Xi′an metro line No.5 crossing underneath line No.2 (unit:m)

2 盾殼與土體摩擦力計算公式及數值實現

2.1 盾殼與土體摩擦力計算公式

關于盾殼與土體摩擦力的計算，文獻[18]通過將盾構兩側土壓力簡化為均布壓力，給出了簡化的計算模型，如圖3(a)所示；考慮盾構兩側實際土壓力的分布，本文對摩擦力計算公式進行了改進，如圖3(b)所示。

(a)簡化計算模型

側向土壓力qe與豎向土壓力pe1、pe2在盾構徑向的分力p1、p2之和為支持力的大小，其中側向土壓力qe左右對稱，計算公式為：

qe=Kγ[hN+r(1-sinθ)]。

(1)

式中：K為盾構所處地層的靜止側壓力系數，一般按K=1-sinφ計算，φ為土體內摩擦角，(°);γ為土體容重，kN/m3；hN為盾構頂部埋深，m。

故側向土壓力在盾構徑向單位長度的分力p1計算公式為：

dp1=[KγhNcosθ+Kγr(1-sinθ)cosθ]rdθ。

(2)

對于豎向土壓力，考慮到盾構自重對底部土體的作用，其頂部土壓力與底部土壓力計算公式分別為：

pe1=γ[hN+r(1-sinθ)]；

(3)

(4)

式(3)—(4)中：W為盾構自重，kN;r為盾構刀盤半徑，m；lsh為盾構長度，m。

故豎向土壓力在盾構徑向單位長度上、下部分的分力P2的計算公式分別為：

dp2上={γ(K+1)[hN+r(1-sinθ)]}rdθ；

(5)

(6)

因此，盾構與周圍土體摩擦力的計算公式分別為：

dFf1=η(dp1+dp2上)dlsh；

(7)

dFf2=η(dp1+dp2下)dlsh。

(8)

根據式(7)—(8)，盾殼與周圍土體摩擦力分布形式如圖4所示，表現為：1)盾殼與土體之間的摩擦力呈現上部小、下部大的特點(原因其一為盾構自重引起底部土體產生抗力，造成土體與盾殼之間接觸壓力的增大，進而引起摩擦力的增大；其二為深度不同造成盾構頂部與底部所受豎向、側向土壓力的差異)；2)摩擦力沿盾殼四周不均勻分布，且其分布形式與內摩擦角、盾構埋深、土體重度的改變無關，摩擦力最大位置為盾構下部與水平面約呈70°夾角處，摩擦力最小位置為盾構最左與最右側；3)摩擦力大小與內摩擦角、隧道埋深、土體重度呈正相關性，但各因素對摩擦力的影響原因不同，內摩擦角的增大不僅造成摩擦系數的增長，同時也能導致靜止側壓力系數的增大、水平土壓力的增大進而引起土壓力徑向分力的增大，而埋深與重度的變化僅能造成土壓力在徑向分力的變化。

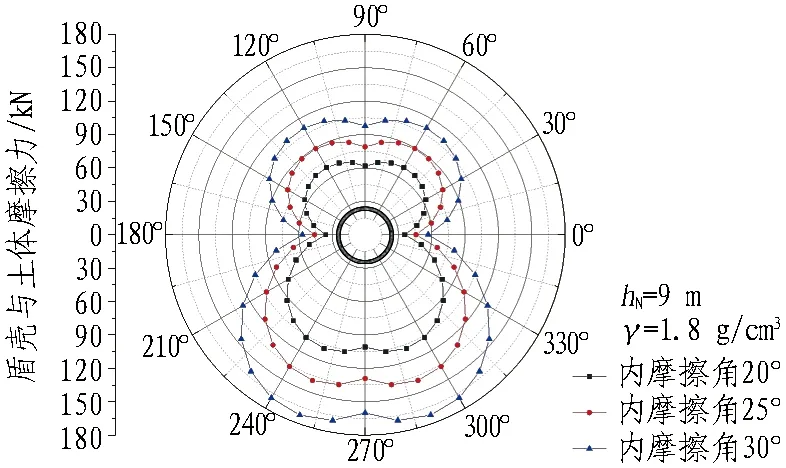
(a)

2.2 盾構施工參數計算及施工區段劃分

根據文獻[9-10]，目前常用的盾構土艙壓力計算公式為：

pe=σh=K∑γh。

(9)

式中：pe為盾構土艙壓力，kPa;γ為土體重度，kN/m3;σh為水平土壓力；h為盾構隧道拱頂埋深。

注漿壓力計算公式為：

(10)

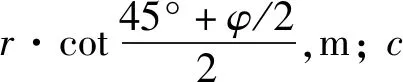
根據式(9)—(10)，可求得本工程基準土艙壓力為0.18 MPa，注漿壓力為0.25 MPa。

盾構近距離下穿已建隧道時由于已建隧道部位土體被置換成隧道結構，其正面土壓力值會發生顯著變化[20]，因此，穿越中心水平土壓力應為：

σh=K[γ(h1+h2)+T]。

(11)

式中：h1為既有隧道拱頂埋深，m;h2為既有隧道與新建隧道凈距，m;T為既有隧道結構單位長度自重。

根據式(11)，本工程下穿中心土艙壓力為0.14 MPa。考慮到注漿壓力過大對既有隧道底部土體的擾動過大，結合工程實際取下穿段注漿壓力為0.20 MPa。考慮到盾構施工每環土艙壓力調整量不宜大于10 kPa，若每環調整過大，則易對既有隧道產生較大擾動，因此盾構施工參數由正常掘進參數調整到下穿參數時需要過渡區間。

結合文獻[21]所述盾構隧道施工的影響范圍，盾構下穿既有結構時次要影響范圍

lI=(D+h2+2r)tanα。

(12)

式中：D為既有地鐵隧道等效直徑，m，可用等代圓法計算；α為盾構隧道影響角，(°)，取值范圍一般為5°±φ/2。

根據式(12)，則本工程各區段長度分別為：

l1=l3=lI=13.37 m；

(13)

l2=2D+lS=21 m。

(14)

式(13)—(14)中：l1，l2，l3分別為接近區、穿越區和脫離區區段的長度；lS為既有隧道間距。

最終，本文選定既有隧道兩側一定范圍為調整區間，設計了盾構下穿的工況設計方案，如表1及圖5所示。

表1 盾構下穿施工參數設計方案Table 1 Construction parameters for shield tunneling MPa

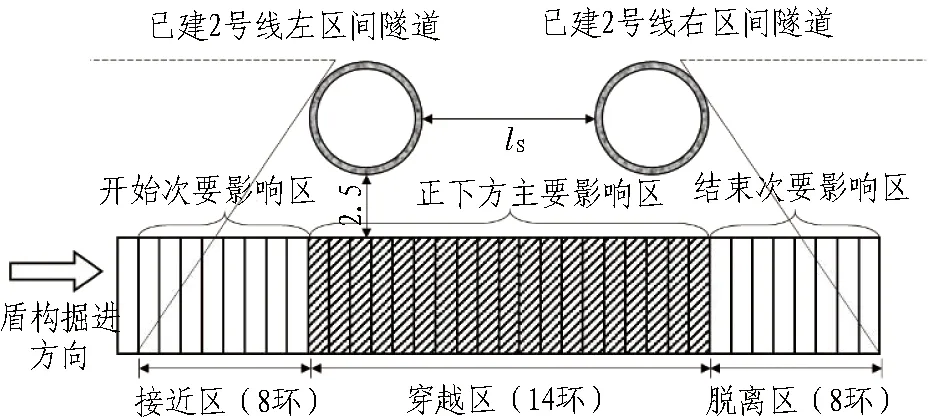
圖5 盾構下穿既有隧道分區示意圖Fig.5 Segmentation of shield tunnel crossing underneath existing tunnel

2.3 數值實現

2.3.1 模型概況

根據隧道結構實際尺寸及圣維南原理，沿新建隧道軸線取70 m，沿既有地鐵方向取70 m，上部地層取至地表，既有區間隧道結構與新建隧道間距2.5 m，如圖6所示，模型最終大小為70 m×70 m×60 m。最終，模型共包括節點152 606個，單元307 402個。土層及隧道襯砌結構材料物理力學參數分別如表2和表3所示。土體采用摩爾-庫侖模型，既有隧道襯砌結構及新建盾構管片單元均采用彈性體模型；對模型底部及四周施加約束，上表面為自由面。注漿體等代層物理參數依據文獻[11]和[22]并結合盾構掘進試驗段漿液抗壓強度現場測試結果擬定。

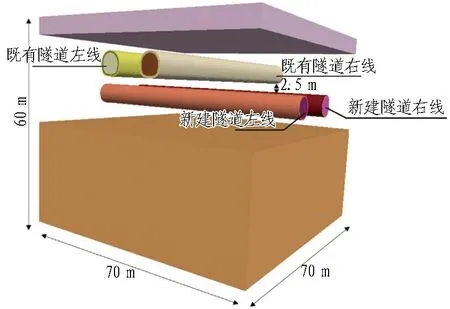
圖6 計算模型Fig.6 Calculation model

2.3.2 盾構下穿施工過程模擬

新建5號線盾構隧道采用剛度遷移法進行模擬(見圖7)，每次循環開挖一個管片長度(1.5 m)；考慮盾構的長度及質量，對盾殼單元采用彈性體模型，根據工程實際賦予相應的重度、彈性模量等參數，土艙壓力通過對掌子面施加面荷載模擬，注漿壓力通過對土體施加徑向荷載模擬，摩擦力通過對盾殼外圍土體施加對應大小的橫向荷載模擬，頂推力通過對管片單元施加節點力模擬。根據計算公式，摩擦力并不是均勻分布在盾殼與土體接觸面上的，每一點處的摩擦力大小均與該點對應的坐標和角度有關，因此本文通過FLAC 3D內置的Fish語言，以角度和坐標為變量，在與盾殼接觸的土體部分施加對應大小的荷載的方法，模擬摩擦力對土體的影響，以提升數值計算結果的準確性，使其結果更加貼合實際工程。

表2 土層物理力學參數Table 2 Physico-mechanical parameters of soil

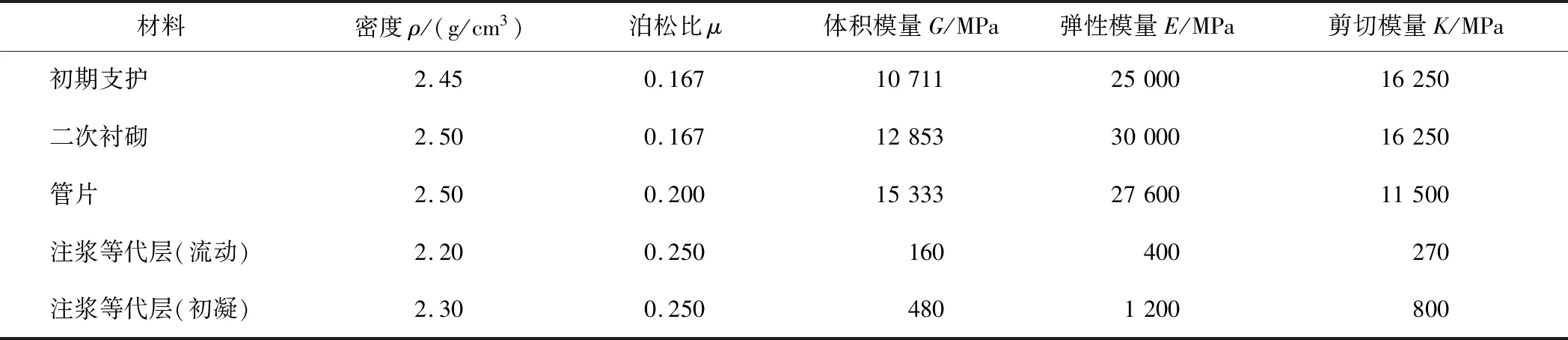
表3 材料物理力學參數Table 3 Physico-mechanical parameters of material

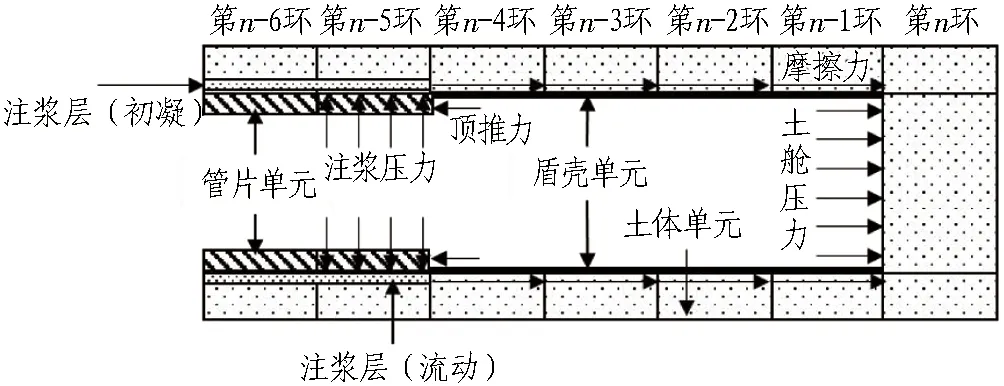
n代表盾構掘進時的環數。圖7 新建盾構隧道施工過程模擬Fig.7 Simulation of construction process of shield tunnel

2.3.3 監測點布置

由于既有隧道受盾構施工擾動最大的位置一般位于其與新建隧道軸向交叉處，故在新建隧道軸向上方的既有隧道斷面處設置拱頂、仰拱、拱腰4個監測點，如圖8所示。

圖8 既有隧道監測點設置圖Fig.8 Layout of monitoring points for existing tunnel

3 計算結果分析

3.1 盾構逐環掘進中既有隧道結構位移規律

圖9示出各工況既有隧道結構拱頂、仰拱、拱腰隨盾構逐環推進的位移曲線，由圖可知：1)既有隧道拱頂、拱腰、仰拱處的豎向位移趨勢均表現為先隆起、后沉降，各位置在盾尾脫離前一直保持隆起趨勢，且隨著刀盤接近，結構隆起逐步增大；而在盾構通過、壓力消散后，各處變形曲線下降，隆起變形量均逐漸減小，表現為沉降趨勢。既有隧道結構隆起的原因是盾構掘進對前方土體的擠壓作用，土艙壓力的施加使得前方土體產生附加接觸壓力[23-24]，摩擦力引起盾構四周土體產生與隧道掘進方向一致的水平位移，二者均引起前方地層的隆起，并進而造成既有結構隨土體產生隆起位移。2)對比分析既有隧道結構豎向變形可知，各位置隆起量、橫向水平位移量從大到小依次為右側拱腰>仰拱>拱頂>左側拱腰，右側和左側拱腰最大隆起量差分別為2.22、2.01 mm，橫向水平位移差分別為1.98、1.70 mm。而位移曲線增長的區間與其受土艙壓力、摩擦力、注漿壓力綜合作用的時間一致，各因素對右側拱腰作用時間最長，拱頂與仰拱次之，左側拱腰最短，故結構各處隆起量大小及隆起趨勢持續時間主要取決于其受盾構掘進過程中土艙壓力、注漿壓力、摩擦力作用的時長。3)由于盾構掘進先下穿通過既有隧道左線后下穿右線，土艙壓力、注漿壓力、摩擦力對左右線既有隧道作用的時間不同，造成變形曲線中二者量值、增減趨勢的差異；在豎向位移方面，右線既有隧道結構與左線拱頂、仰拱、左側拱腰、右側拱腰最大隆起量差分別約為1.96、1.98、1.82、2.01 mm；橫向水平位移方面，左右線既有結構橫向位移均表現為隨刀盤接近而增大，盾尾通過后逐漸穩定的趨勢，二者最大變形量差較小，拱頂、仰拱、左側拱腰、右側拱腰4個監測點分別為0.19、0.46、0.33、0.30 mm，但隧道左右線結構變形穩定所需的時間不同，左線水平變形約在盾構掘進至35環時穩定，右線則需在掘進至45環時才趨于穩定。

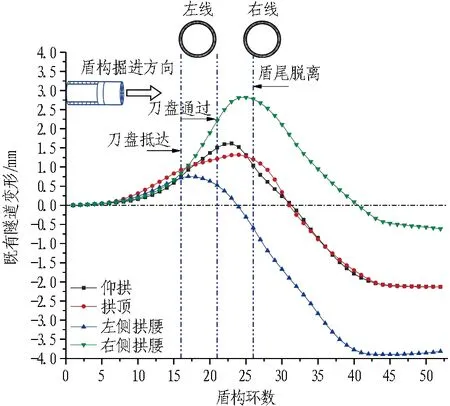
(a)既有隧道左線豎向位移

3.2 既有結構位移影響因素研究

選取土艙壓力pe=0.09～0.18 MPa、注漿壓力pg=0.10～0.25 MPa、摩擦因數ηf=0.20～0.50，對比不同工況下既有左線隧道右拱腰豎向位移進行影響分析。不同土艙壓力條件下既有結構位移曲線見圖10，由圖可知，隨著土艙壓力的增大，既有結構在刀盤到達前(0—21環)的隆起趨勢增強，在盾構通過時(16—26環)的隆起值增大，盾尾脫離至施工完成階段(26—52環)的沉降值減小。各工況豎向變形曲線之差在盾構下穿段逐漸增大，在盾尾脫離處達到最大，結合圖11和12中盾尾脫離前(0—26環)各曲線相差極小，表明此過程既有結構豎向位移受土艙壓力影響程度最深；而在盾構離開后不同工況既有結構豎向位移差值變動較小，施工完成后其沉降大小差異的原因為先前隆起量的不同，表明盾構脫離后既有結構豎向位移受土艙壓力影響程度較小，故土艙壓力的主要作用區間為盾尾脫離前(0—26環)。

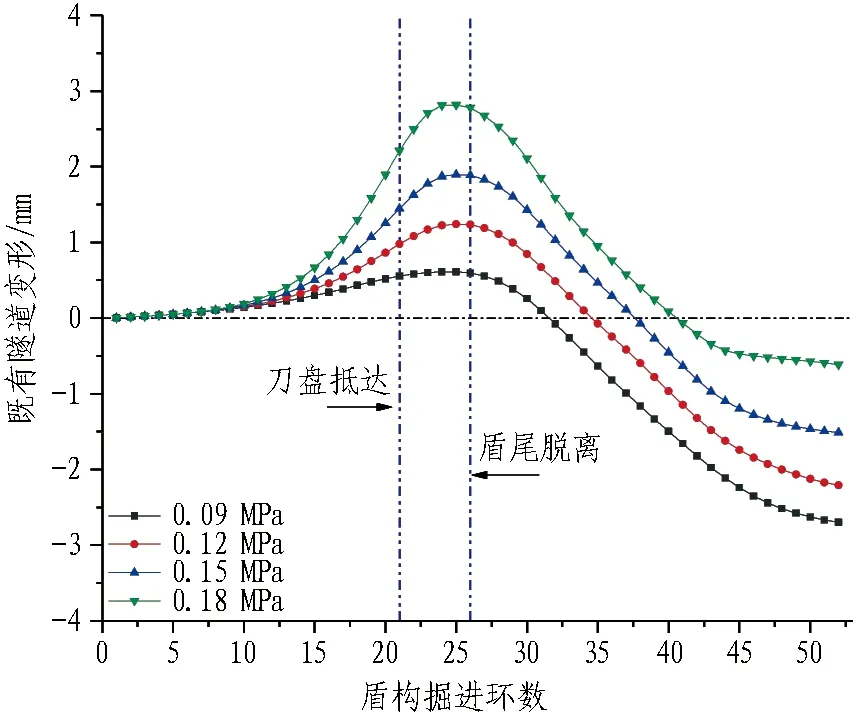
圖10 不同土艙壓力條件下既有結構位移曲線Fig.10 Displacement of existing structure under different soil chamber pressures

不同注漿壓力條件下既有結構位移曲線見圖11，由圖可知，注漿壓力的變動對盾尾脫離前既有結構豎向位移變化并無明顯作用，其對既有結構位移的主要影響區段應為盾尾脫離至施工完成階段(26—52環)，且表現為隨著注漿壓力的增大，作用在盾尾空隙上的支護壓力增大，既有結構在盾構通過后的沉降量減小，沉降趨勢放緩。因此，為減小盾構通過后地層及既有結構的沉降，應及時進行盾尾注漿，并設置合理的注漿壓力。

不同摩擦因數下既有結構變形曲線見圖12，由圖可知，摩擦力對既有結構位移的影響區段可分為盾構機身通過階段(21—26環)與盾尾脫離后階段(26—52環)。在盾構機身通過階段，結構隆起量隨著摩擦力的增大而增加，而盾尾脫離后隨著摩擦力的增大，既有結構豎向沉降值及沉降趨勢逐漸增大。其原因應為盾構機身通過時摩擦力帶動周圍土體產生與掘進方向一致的水平位移，土體向前位移引起前方地層隆起，使既有結構隨之向上隆起；而盾構通過后摩擦力又造成盾尾后方空隙增大，上方地層向下移動填補空隙，造成了地層沉降的加劇，并使得既有隧道隨之產生沉降，因此，過大的摩擦力對地層及既有結構的穩定有較大負面影響，工程中應及時向盾殼周圍注入膨潤土泥漿，以盡量減少盾構掘進時盾殼與土體之間的摩擦力。

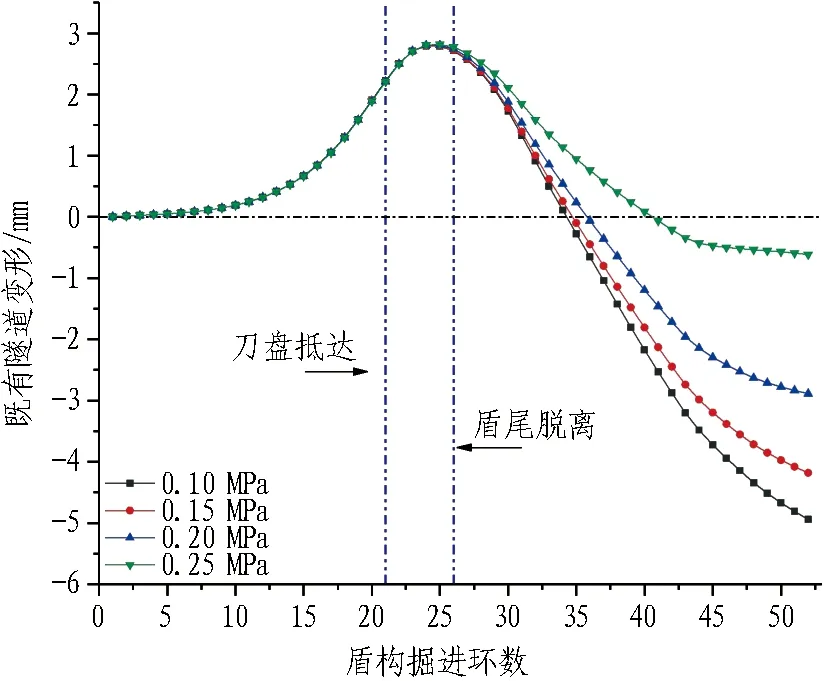
圖11 不同注漿壓力條件下既有結構位移曲線Fig.11 Displacement of existing structure under different grouting pressures

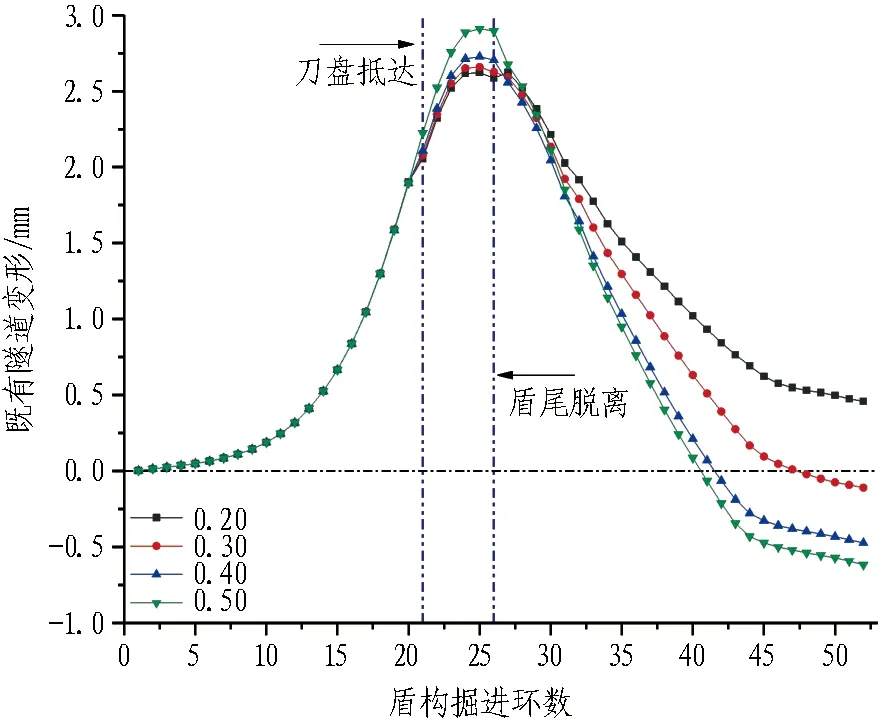
圖12 不同摩擦因數下既有結構變形曲線Fig.12 Displacement of existing structure under different friction coefficients

4 現場實施效果評價

4.1 現場監測點布設

為評價2.2節計算給出的盾構下穿施工參數、參數調整區間對已建2號線區間隧道變形的控制效果，并驗證數值計算結果的準確性，在盾構施工影響范圍(DK15+389～+449)內設置11個監測斷面，如圖13所示；在每個監測斷面內左右線隧道軌道道床及拱頂設置A—F6個監測點，如圖14所示，對既有區間隧道變形進行監測。

圖13 監測斷面布設圖Fig.13 Layout of monitoring section

圖14 現場監測點布設圖Fig.14 Layout of monitoring points

4.2 現場監測結果分析

雙線盾構隧道施工完成后，實測既有區間隧道左右線道床變形及數值模擬計算結果如圖15所示。本文采用考慮摩擦力的計算模型，其結果與實測值誤差為11%，較以往不考慮摩擦力計算模型小24%，且小于均勻分布模型的15%，表明了該模擬方法的正確性。實測值與計算曲線均表現為：道床最大變形處位于左線盾構隧道與其交叉位置測點；右線道床最大沉降處位于右線盾構隧道與既有隧道交叉位置測點處，對于盾構下穿工程而言，由于盾構施工中土體及土中隧道結構與盾構的距離最近，受施工參數影響最大，且施工后受施工影響原先被擠壓的土體在盾構通過后孔隙水壓的降低、釋放會發生沉降，所以受盾構擾動最大的部分應當為新建隧道與既有隧道交叉位置，實際施工中應當對此區域多加監測；另外，既有隧道左右線道床變形雖略有不同，但最大沉降均小于6 mm，最大上浮小于5 mm，滿足GB 50911—2013《城市軌道交通工程監測技術規范》[21]、CJJ/T 202—2013《城市軌道交通結構安全保護技術規范》[25]中的要求，因此本文確定的施工參數對于控制道床變形起到良好效果。

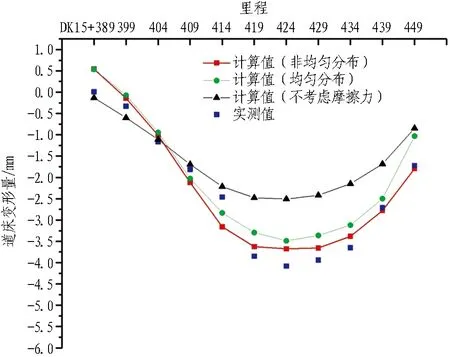
(a)既有隧道左線道床A測點變形

圖16示出既有2號線區間隧道襯砌拱頂沉降變化及實測與計算對比。實測值與本模型計算結果偏差較小，誤差約14%，遠小于不考慮摩擦力計算模型的31%，且小于均勻分布模型的23%。與道床沉降類似，隧道拱頂變形曲線較為符合“沉降槽曲線”[26-27]的形式，最大沉降處位于盾構隧道中心線上方，距離盾構軸線越遠沉降量越小；右線隧道拱頂沉降整體較小，最大沉降僅為1.91 mm，證明了施工盾構參數調整較為及時有效；在采用本文所提出的施工參數調整后，既有隧道左右線最大拱頂沉降量均小于6 mm，符合GB 50911—2013《城市軌道交通工程監測技術規范》[21]、CJJ/T 202—2013《城市軌道交通結構安全保護技術規范》[25]中的要求，因此本文確定的施工參數對于拱頂沉降的控制效果也較為理想。

(a)既有隧道左線E測點變形

5 結論與建議

1)考慮盾殼自重及盾構四周土壓力的分布特征，推導了盾殼-土體摩擦力的計算公式，分析了其分布特征，并基于Fish語言應用于FLAC 3D中，較為真實地反映了盾構下穿過程中盾殼與土體之間摩擦力對既有結構的影響。

2)在下穿過程中，既有隧道結構豎向變形表現為隨盾構逐環推進結構逐漸隆起，在盾構離開、壓力消散后呈現沉降的趨勢；橫向水平位移則表現為隨盾構接近而逐漸增大，盾尾通過后逐漸穩定；由于土艙壓力、摩擦力、注漿壓力擾動程度不同，左右線隧道結構之間、隧道不同結構之間變形差異較大，兩隧道結構變形量由大至小依次為右側拱腰>仰拱>拱頂>左側拱腰；既有結構隆起為右線大于左線。

3)在盾構下穿的不同階段，既有結構豎向位移的主要影響因素不同。在刀盤到達前，既有結構的隆起主要受土艙壓力影響；而在盾構機身通過時，既有結構的豎向隆起隨土艙壓力、摩擦力的增大而增大；在盾尾通過后，既有結構的沉降隨注漿壓力的增大以及摩擦力的減小而減小。因此，應設置合理的施工參數，并及時注入膨潤土泥漿等措施減小摩擦力，以穩定開挖面、減少地層及既有結構的沉降。

4)根據現場實測數據反饋，本模型計算結果與實測值偏差分別約為10%和14%，小于不考慮摩擦力和均勻分布摩擦力的計算模型，驗證了本文對摩擦力影響分析的合理性及數值模擬方法的準確性；既有運營中2號線隧道道床最大變形量及拱頂最大沉降量均小于規范所要求的6 mm，表明本文所確定的盾構施工參數及參數調整方法對于控制本工程既有隧道變形、保障運營安全起到了良好的控制作用。

5)由于本文在計算過程中未考慮地下水、運營列車荷載、地面建筑物的影響，造成計算結果與實測值仍有一定偏差，因此，建議在之后的研究中可針對以上因素進行更加全面細致的分析。