基于單擺和拾振彈簧的漂浮式波浪能發電裝置研究

王志華，王光震，姚 濤，呂殿利，周 嚴

（1.省部共建電工裝備可靠性與智能化國家重點實驗室（河北工業大學 電氣工程學院），天津 300130；2.河北省電磁場與電器可靠性重點實驗室（河北工業大學電氣工程學院），天津 300130；3.河北工業大學機械工程學院，天津 300130；4.天津商業大學 理學院，天津 300134）

0 引言

波浪能是可再生能源的重要組成部分，全球每年可利用的波浪能為2 GkW，中國海域的最大波浪能量密度可達7 kW/m[1]。不同于太陽能板間歇性的發電方式，只要有波浪激勵，波浪能發電裝置就能無間歇發電，可以時時刻刻為海洋上的漂浮式傳感器節點供電。

傳統的漂浮式波浪能發電裝置采用直線式發電機原理，在波浪的驅動下使得永磁體與感應線圈產生相對直線運動，在感應線圈中產生電動勢[2]。根據此原理制作的一種小型圓筒形浮標波浪能發電系統能夠在波高為0.8 m，周期為3 s的情況下，產生幅值為0.4 V的空載感應電動勢[3]。在幅值為0.3 m的豎直位移激勵下，一種由彈簧、滑動質量塊和阻尼系統構成的雙共振波浪能量轉換器輸出的機械功率約為18 W[4]。有學者將波浪的直線運動轉換為旋轉運動，從而減少了由往復式直線運動的慣性造成的機械能損失。一種借鑒了機械手表的波浪能發電裝置可以通過自動陀的擺動帶動齒輪轉動為發條儲能[5]，但是該裝置無任何實驗數據支持，并且裝置中的傳動齒輪較多，要求裝配精度較高，其實用性和可靠性還有待于進一步驗證。隨著新型聚合物發電材料的研制，一些學者也開始將其應用在波浪能發電裝置上。在波浪頻率為2 Hz的情況下，利用多層摩擦納米材料發電機制作的漂浮式波浪發電裝置輸出的平均功率密度為13.2 mW/m2[6]。在波高為8 cm，頻率為0.5 Hz的條件下，采用多光柵摩擦納米發電機制作的波浪能發電裝置的最大即時輸出功率為54 W，最大即時輸出功率密度為4.2 mW/m2[7]。

綜上所述，相比于利用新型聚合物材料發電，利用電磁感應原理制作的電磁式波浪能發電裝置的功率依然是最高的。由于漂浮式波浪能發電裝置受到的是位移激勵，不適合采用傳統直線發電機的磁路結構，因此，本文基于盤式電機發電原理提出了一種新型的基于單擺和拾振彈簧的波浪能發電裝置。首先給出該裝置的結構設計和工作原理，然后對裝置的響應過程進行數學分析和仿真計算，最后制作樣機進行實驗測試。本研究可為漂浮式波浪能發電裝置的應用提供理論支持和實驗依據。

1 理論分析

1.1 結構設計

本文設計的波浪能發電裝置的內部結構和發電原理如圖1所示。

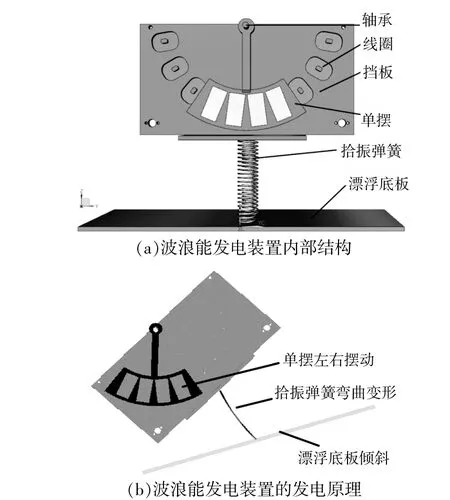
圖1 波浪能發電裝置的內部結構和發電原理Fig.1 Wave energy generator internal structure and powergeneration principle

從圖1（a）可以看出，單擺通過軸承與擋板連接，并且有4個永磁體嵌入擺錘的凹槽中作為轉子。發電機的前后擋板各設有9個均勻分布的梯形定子線圈，每個線圈由多匝銅漆包線纏繞而成。若直接使用剛體支撐結構，由于波浪的頻率很低，單擺的擺角很小，難以提高發電功率。因此，使用拾振彈簧機構來改善波浪能發電裝置的擺動角度。拾振彈簧的頂部和底部分別剛性地連接到擺式發電機和底板，底板可固定在海洋浮子上。從圖1（b）可以看出，當波浪使漂浮底板傾斜時，拾振彈簧會發生彎曲變形，帶動發電機左右晃動，同時發電機內部的單擺左右擺動，使固定在發電機前后擋板上的感應線圈中的磁通開始發生變化，在電磁感應作用下線圈中產生一定的感應電動勢，接上負載即可實現波浪能到電能的轉換。

1.2 理論建模

當彈簧做拉伸或壓縮變形時，通常用彈簧剛度來定量描述彈簧受力與形變的關系。但是，在本文的波浪能發電裝置中，拾振彈簧作彎曲運動，在涉及到螺旋彈簧彎曲問題時，可以把螺旋彈簧看作等截面的彈性圓柱體，從而利用普通彈性理論進行分析。波的實際振動非常復雜，通常分為規則波和不規則波運動，在理論分析中常將波浪看作規則的正弦波。本文設計的兩自由度（單擺擺動角度和漂浮底板受到的角位移激勵）漂浮式波浪能發電裝置的簡化模型如圖2所示。

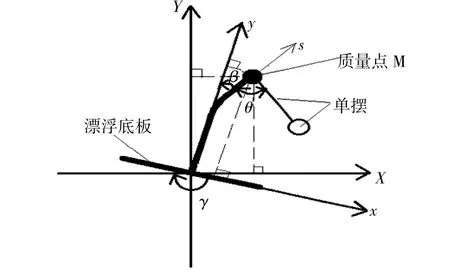
圖2 波浪能發電裝置的簡化模型Fig.2 Wave energy generator simplified model

波浪能發電裝置的前后擋板被簡化為一個質量點M。拾振彈簧簡化為彈性梁[8]，此彈性梁的上、下端分別和質量點M與底板剛性連接，彈性梁本身的質量忽略不計。根據彈性梁的邊界條件，不考慮梁中心線延長，即不考慮梁的軸向變形，只考慮橫向變形[9]。單擺繞質量點M轉動，β（t）為單擺與質量點的相對角位移。分別建立一個靜態的笛卡爾坐標系X-Y和一個隨模型運動的動坐標系xy，兩個坐標系的原點均在梁與底板連接的初始位置處。沿著梁中心曲線的坐標為s，所以當梁彎曲時，彈性梁中心軸線上的點在動坐標系和靜坐系下的坐標分別為[x（s，t），y（s，t）]和[X（s，t），Y（s，t）]。

波浪施加在底板中心處的角位移激勵γ（t）為

式中:M為質量點M的質量，kg；g為重力加速度，m/s2；H為彈性梁的長度，m；·代表對時間t的導數，此定義也適用于下面各式。

單擺的動能T2和重力勢能V2分別為

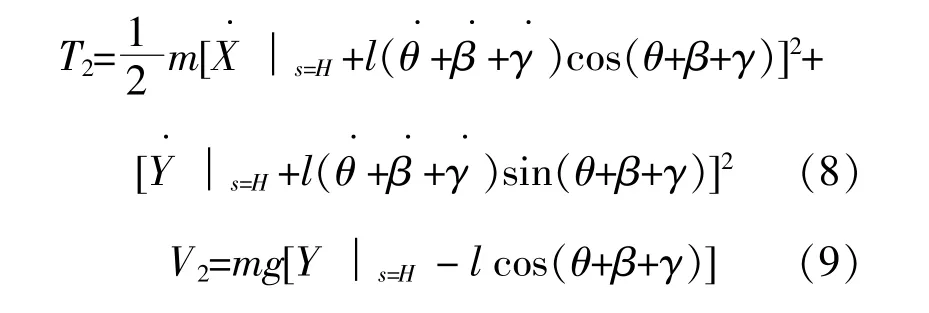
式中:m為單擺的質量，kg；l為擺桿的長度，m；θ·為彈性梁的中心軸線與o-y軸的夾角對時間的變化率，（。）/s；β·為單擺角速度，（。）/s；γ·為波浪施加在底板中心處的激勵角速度，（。）/s。

彈性梁的彎曲勢能V3為

本文模型的哈密爾頓能量方程為

式中:t0，t1為裝置相對位置變化的時間，s；δ×L為L的虛變化。

彈性梁的邊界條件為

由式（11），（14）可消去獨立變量y和θ，將邊界條件（18）代入式（17）并運用有限元的方法，便可解得此模型的運動方程。

根據法拉第電磁感應定律，單擺的擺動將在線圈中產生電動勢。如果發電機與負載耦合，則發電機可以輸出電力并且感應電動勢正比于感應線圈中磁通的變化率。而磁通的變化率又正比于動子和定子的相對位移，即單擺角位移β（t），則波浪能發電裝置的輸出感應電動勢為

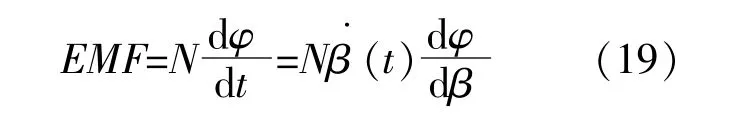
式中:N為線圈總匝數；φ為線圈的磁通，Wb；β·（t）為單擺的角速度，（。）/s。

1.3 理論效率計算

假設波浪高度為Hw，波浪周期為T，則發電裝置受到波浪作用的平均功率Pm為[10]

式中:ρ為海水密度，kg/m3；R為波浪發電裝置所用浮子的等效半徑，m。

當負載阻值RL和波浪能發電裝置的內阻Rin相等時，波浪能發電裝置的最大輸出功率Pe為

式中:Uoc為發電裝置的空載輸出電壓，V；Rin為發電裝置的內阻，Ω。

波浪能發電裝置的理論最大發電效率ηmax為

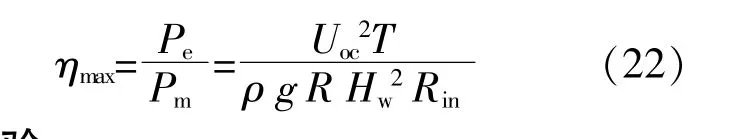
2 仿真實驗

2.1 運動仿真實驗

在實際工程中，經常用海浪運動分析理論-線性波理論把規則的波浪運動看作正弦運動[11]。根據中國國家標準《小型海洋環境監測浮標》規定，小型浮標（直徑小于3 m）的最大傾斜角不大于30。，自搖周期不大于3 s[12]。綜上所述，設波浪對漂浮底板中心處的激勵角位移為γ（t）=30 sin（2.1t），波浪能發電裝置的相關參數為M=2 kg，m=0.25 kg，l=80 mm，考慮到波浪能發電裝置的重心不宜過高，設拾振彈簧的初始長度為0.1 m。當拾振彈簧的彎曲剛度分別為2.4×105，1.3×105N·mm2和使用剛體支撐結構時，單擺角位移的變化規律如圖3所示。

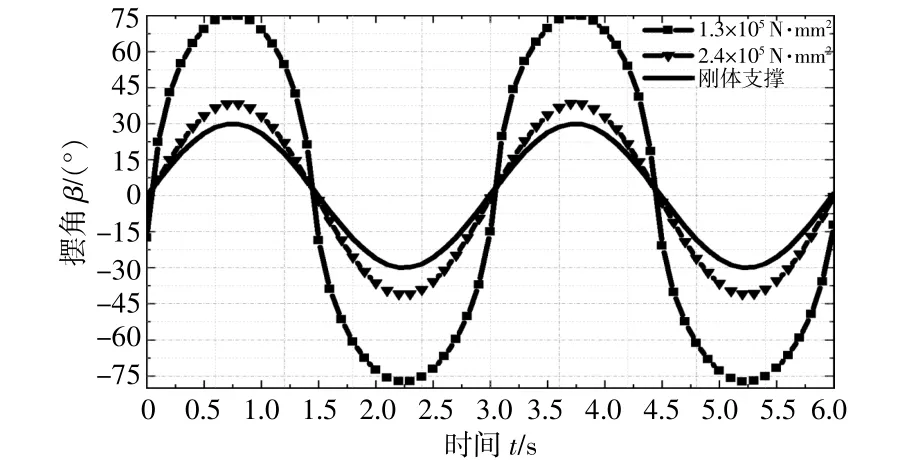
圖3 單擺角位移隨時間的變化Fig.3 Vibration of single pendulum angular displacement with time

從圖3可以看出:單擺角位移呈現出周期性的正弦曲線的變化規律，當使用剛體支撐結構時，單擺角位移和輸入的激勵轉矩角位移相同；當拾振彈簧的彎曲剛度為2.4×105N·mm2時，單擺的最大角位移約為40。，是輸入的激勵轉矩角位移的1.3倍；當拾振彈簧的彎曲剛度為1.3×105N·mm2時，擺動幅值增大到75。，單擺角位移是輸入的激勵轉矩角位移的2.5倍。綜上可知，本文設計的拾振彈簧結構可以將激勵角位移放大。

2.2 電磁仿真實驗

利用COMSOLR有限元軟件對波浪能發電裝置的磁場分布進行分析，此次仿真設計的動子永磁體采用釹鐵硼材料，相對磁導率為1.1，長×寬×高為40 mm×20 mm×10 mm。定子線圈選用銅導線，相對磁導率為1.0，匝數為400匝，永磁體與線圈的氣隙為1 mm。根據磁場分布計算結果，再結合動子和定子的位移方程和電磁感應定律，可計算得到發電裝置的輸出三相空載電動勢u（u1，u2和u3）。電磁仿真實驗結果如圖4所示。從圖4可以看出:當拾振彈簧彎曲剛度為1.3×105N·mm2時，u的有效值分別為1.97，2.05，2.11 V；當拾振彈簧彎曲剛度為2.4×105N·mm2時，u的有效值分別為1.33，1.46，1.21 V；當使用剛體支撐時，u的有效值分別為0.71，0.73，0.69 V；當拾振彈簧彎曲剛度為1.3×105N·mm2，頻率為5 Hz時，發電裝置的空載輸出電動勢幅值達到最大，最大值為18 V。對比以上仿真結果可知，在同等時間和相同激勵的情況下，使用拾振彈簧結構比使用剛體支撐時的輸出空載電壓有效值大2～3倍，并且拾振彈簧的彎曲剛度越小，輸出的三相空載電動勢越大。這是因為在相同的位移激勵下，拾振彈簧彎曲剛度越小，彈簧形變越大，提高了單擺動子與線圈定子的相對運動角速度，增加了磁鏈與動子和定子的相對角位移的變化率。

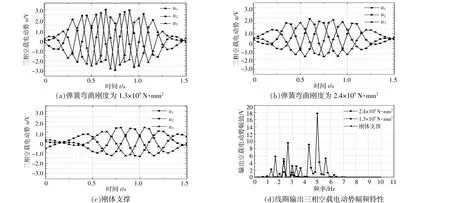
圖4 電磁仿真實驗結果Fig.4 The results of electromagnetic simulation experiment

3 樣機實驗

3.1 空載實驗

為驗證波浪能發電裝置的發電性能，按上述仿真實驗設計的裝置參數制作了波浪發電裝置樣機，其中拾振彈簧彎曲剛度EI為1.3×105N·mm2，搭載樣機的浮子等效半徑R為0.2 m。為了利用波浪能發電裝置所產生的電能，設計了電能處理電路。將樣機放在水槽中并在水槽一端施加幅值為5 cm，頻率為3 Hz的豎直位移激勵。經過測量計算，此時波高約為4.0 cm，頻率約為1 Hz，由式（20）計算可得此時波浪作用在浮子上的平均機械功率Pm為0.80 W。將電能輸出端與電能處理電路輸入端連接，用TektronixDPO3014R型示波器記錄樣機輸出的三相空載電動勢和整流濾波升壓后的電壓，記錄結果如圖5所示。從圖5可以看出:u1，u2，u3的有效值分別為2.34，2.23，2.38 V；經電能處理電路整流濾波穩壓后的電壓U為5.2 V，電壓紋波約為0.1 8 V；輸出電動勢的頻率主要集中在5～6 Hz，這是因為本裝置為剛彈耦合的非線性系統，使得輸出電動勢信號具有非線性特征，其頻率在一定范圍內進行分布，不再是與輸入激勵同頻的信號。

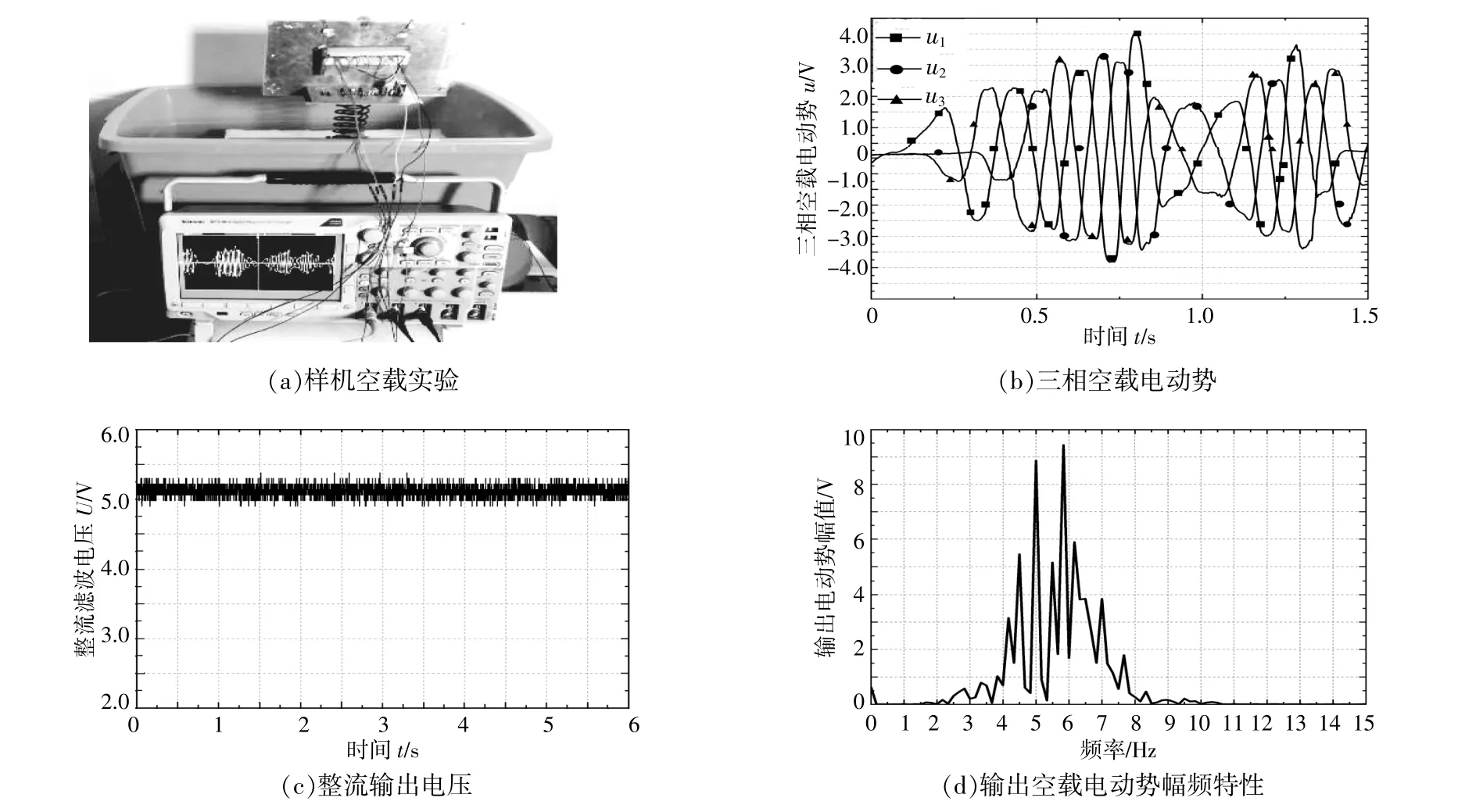
圖5 樣機空載實驗結果Fig.5 No-load test results of the prototype

3.2 負載實驗

本實驗將容量為4 F的超級電容兩端并聯在電能處理電路的輸出端作為負載，并在水槽中施加與上述空載實驗相同的激勵，負載實驗結果如圖6所示。從圖6（a）可以看出:大約經過200 s，超級電容兩端電壓從0.1 V上升到5.2 V，電壓上升速度為25.5 mV/s；流經電容器的電流最大值為0.3 5 A；整個充電過程的電流呈逐漸降低的趨勢，電壓從0.1 V上升到3.5 V的過程用時較短，約為60 s，從3.5 V上升到5.2 V的過程用時較長，約為140 s。這是因為整個充電過程近似于恒壓充電，隨著充電過程進行，電容兩端電壓與電源電壓的差值越來越小，使得充電過程變得緩慢。由圖6（b）可以看出，波浪能發電裝置輸出的最大瞬時功率為0.97 W，平均輸出功率為0.46 W，發電效率為57.5%，可滿足小型電子設備的供電需求。從圖6（c）可以看出，如果波浪能發電裝置采用普通剛體支撐結構，在相同輸入激勵下，超級電容兩端電壓從0.1V上升到5.1 V大約需要465 s，電壓上升速度為10.8 mV/s。對比圖6（a）可知，當波浪能發電裝置使用拾振彈簧結構給超級電容充電時，超級電容電壓的上升速度是使用普通剛體支撐結構時的2.4倍，這說明單擺加拾振彈簧結構能夠有效提高裝置的發電功率。由圖6（d）可以看出，將額定功率為1 W的LED燈泡接在超級電容兩端，燈泡可以被點亮。

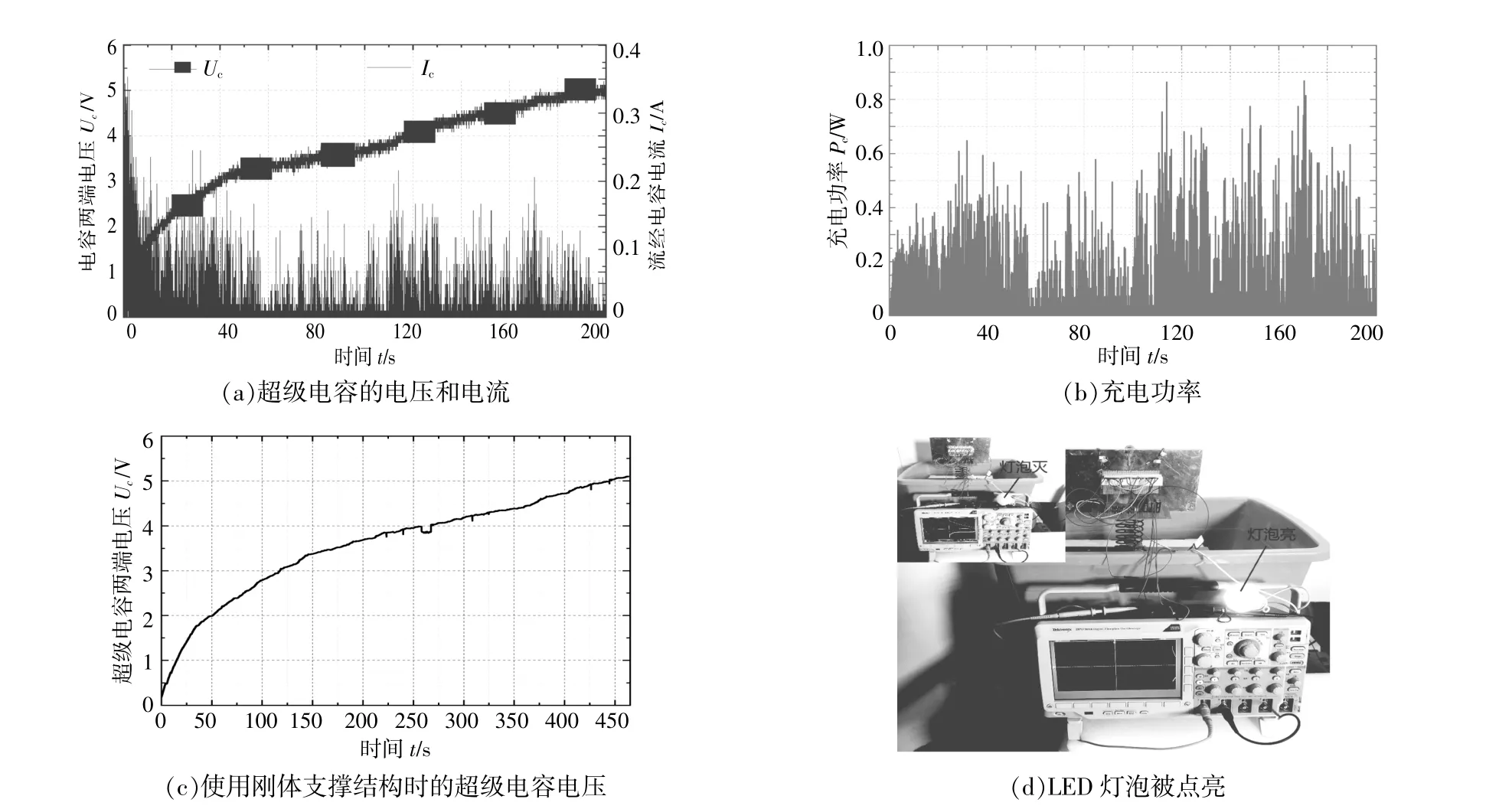
圖6 樣機負載實驗Fig.6 Load experiment of the prototype

4 結論

①通過拾振彈簧結構可以將波浪作用于發電裝置的小角度激勵放大為單擺大角度的轉動，可有效增加動子與定子的相對位移，有利于提高波浪能發電裝置的發電功率。

②當正弦轉矩激勵的幅值為30。，周期為3 s時，在彎曲剛度為1.3×105N·mm2的拾振彈簧作用下，本文設計的波浪能發電裝置能夠將輸入的激勵轉矩角位移放大約2.5倍，裝置輸出的三相空載電壓有效值分別為1.97，2.05，2.11 V。

③在樣機實驗中，當波高為4.0 cm，頻率為1 Hz時，樣機的發電效率為57.5%，輸出電壓為5 V，平均輸出功率為0.46 W，可滿足小型電子設備的供電需求。