注重解題生成 提升核心素養
——對一道解析幾何試題的探究與延伸

北京師范大學鹽城附屬學校 (224007) 郝文華

1 試題

此題是高三復習過程中遇到的一道模擬訓練題，其背景常規、難易適中、內涵豐富、條件清晰、易于上手.問題(1)較為基礎，問題(2)主要考查直線和拋物線的位置關系及韋達定理的應用，屬定值問題，需要學生有一定的運算能力和分析解決問題的能力.筆者在教學的過程中，以問題鏈的形式引導學生深入思考、逐層探究，繼而引出了一連串有價值的探究內容，學生在探究、拓展、延伸的過程中，實現了“問題驅動思維，思維成就素養”的教學理念.

2 探究過程

原解答：(1)易求得拋物線C的方程為y2=4x.

本題解法典型，但具有較強的探究價值，因此，在教學時不能只停留在題目的解答上，而應通過對題目條件及結論的進一步觀察、思考、反思，引導學生延伸探究，揭示數學本質，提升學科素養.

探究1 從本題的結論，你能得到直線EA與EB有何關系？

探究2 注意到直線l過焦點F(1,0)，而定點E的坐標為(-1,0)，(準線與于x軸的焦點)，這是不是一種巧合？能否推廣到一般情形？

探究3 注意到焦點F(1,0)與定點E(-1,0)雖為兩特殊點，但關于坐標原點對稱，能否推廣到更一般的情形？

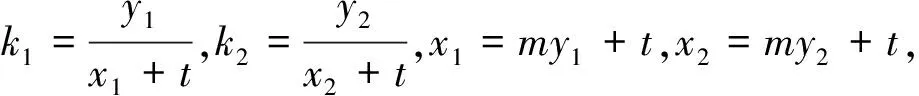
結論已知點G(t,0)與H(-t,0)(t>0)，經過點G(t,0)的直線l與拋物線y2=2px(p>0)交于A，B兩點，直線HA與直線HB的斜率導數之和為0.

3 教學反思

本題是一個典型的圓錐曲線定值問題，講解過程中，并沒有為結論的證明而證明，而是通過題目結論的結構特點，進一步思考探索新的發現，逐步得到拋物線中的一個一般性結論，這對學生圓錐曲線的……