《有序數對》的教學思考

廣東韶關學院數學與統計學院 (512005) 官運和

初中的一些教研活動或教學技能比賽中，經常會選擇《有序數對》這一內容，公開發表有關《有序數對》教學設計的論文也不少，足以說明《有序數對》具有豐富素材.在初中數學教學《有序數對》的過程中，經常出現一些現象：把握學生的認知基礎不到位，把握教材不夠全面，知識理解不透，設定教學目標不準確，揭示數學思想方法不理想，講解“有序”的有效性出現偏差，過度練習時有發生，等等.

一、教學案例

從七年級下學期《有序數對》的實際課堂教學與一些公開發表的論文介紹的關于《有序數對》的教學設計來看，不少老師是這樣設計或者類似這樣設計：

環節一：激趣引新.(1)小林的座位在第一列，你能找到他的座位嗎？(2)小林的座位在第三行，你能找到他的座位嗎？(3)小林的座位在第一列、第三行，你能找到他的座位嗎？(4)你認為需要幾個數據能確定一個位置？

如圖1，同學A的座位在第一列、第三行，他的座位記為數對(1,3)，即規定列數寫在前，行數寫在后，請用數對表示同學B、C、D、E的位置.

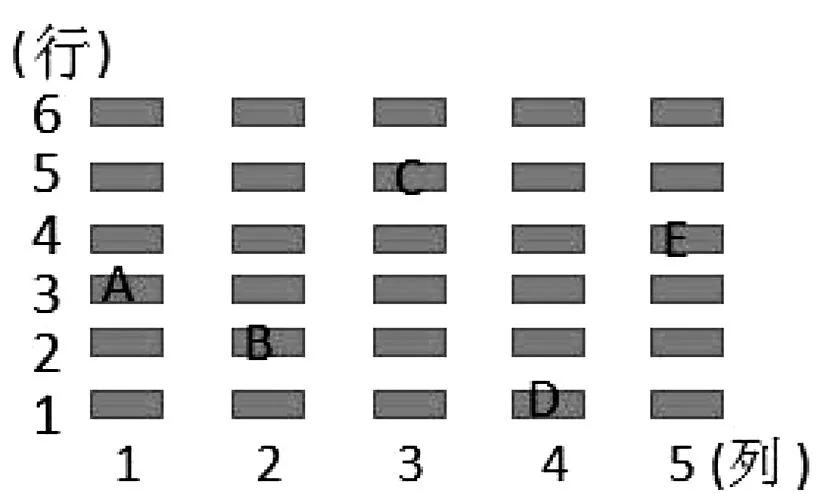
圖1

環節二：探究新知.請座位是(4,3)的同學舉手，結果有二個同學舉手，為什么？因為沒有說前面的4是行數還是列數.從而強調有序數對是有序的二個數.得到定義：我們把這種有順序的兩個數a與b組成的數對，叫做有序數對，記作(a，b).

環節三：知識鞏固.(1)如圖2，實驗樓的位置用有序數對(1,5)表示，請用有序數對表示花壇和其它建筑物的位置；(2)如圖3，魚的位置用有序數對(2,1)表示，請用有序數對表示其它動物的位置；(3)如圖4，B的位置是(2,1)，請表示五角星的五個端點的位置；(4)如圖5，士的位置用有序數對(4,1)表示，請用有序數對表示其它棋子的位置；(5)只有一層的電影院里，若將5排2號記作(5，2)，則4排3號可以表示為( )；(6，7)表示的含義為( ).

圖2

圖3

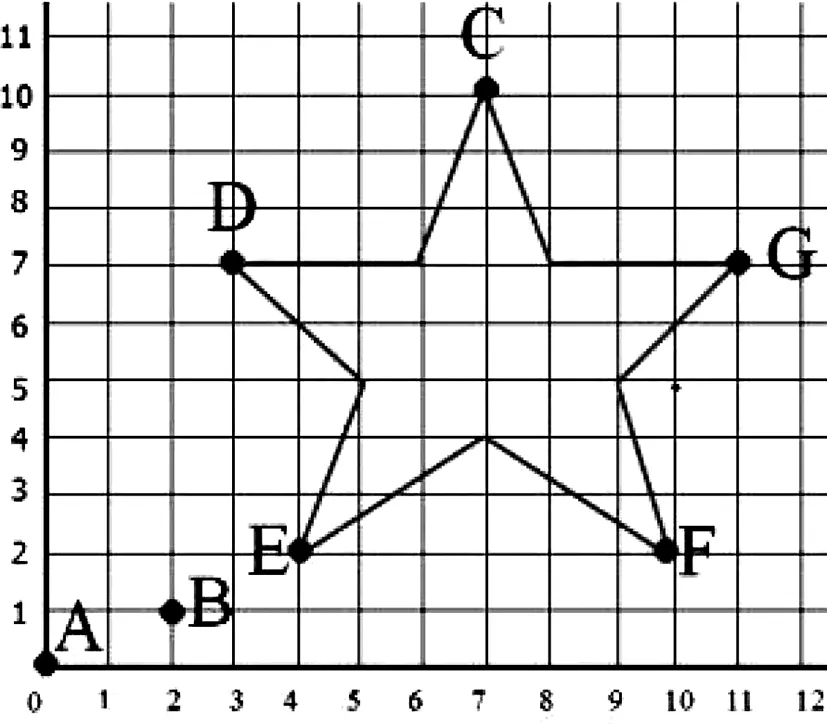
圖4

圖5

環節四：有獎游戲.規定列數在前，行數在后，同時顯示二個同學的座位號，看誰先站起來.

環節五：合作提升.如圖6，小華從A走到B的一條最短路線是：

圖6

A(2,5)→(3,5)→(4,5)→(5,5)→(5,4)→B(5,3).分組討論，寫出小華從A走到B最短的其它路線.總共有幾條？

環節六：課堂總結.學習了數形結合的思想方法.

二、案例分析

以上教學設計有以下幾個方面值得思考：

1.學生的原有認知

小學已學過“用數對確定位置”，在具體情境中，學生能夠在方格紙上用數對(正整數對)表示位置，知道數對與方格紙上點的對應關系.上述教學設計中的知識鞏固環節的教學內容基本上就是小學數學教材上《位置》的內容，另外，小學數學教材上的《位置與方向》是用距離和角度表示位置，是高中極坐標的基礎.初中的《有序數對》屬于提高篇，學習有序數對是從小學中的整數對拓展到實數對，是從用數對確定位置拓展到有序數對確定更多意義上的量.教學這一內容的時候不可低估學生的認知基礎和認知能力.

2.有序數對的理解

3.教學目標的設定

本節是直角坐標系的第一小節，是學習平面直角坐標系的基礎，為建立直角坐標系服務，但不能僅僅停留在為建立直角坐標系服務，有序數對表示平面上點的位置與直角坐標系中用坐標表示點的位置，是一般與特殊的關系，因此這里要突出一般性.由上面的知識的理解的分析也知道有序數對的一般性意義十分廣泛，是培養學生創新能力的很好素材.教學實踐中有的教師始終離不開“行與列”、“直角”，就連菱形的網格都不用，固定在長方形網格，甚至是正方形網格.

4.數學思想方法的揭示

大家都明白數學教學要突出數學思想方法的學習，但在實際教學中往往是在課堂總結的時候，歸納出什么什么數學思想方法，而不是讓學生在學習過程中體驗這種數學思想方法.在有序數對教學的實際課堂中，有的老師在課堂總結中提到數形結合的數學思想方法，但課堂教學中根本就沒體現出來，學生體驗不到由數到形，也體驗不到由形到數，只是看到老師給出的“數形結合”的文字.其實這節課對“一一對應”、“數形結合”、“分類討論”、“特殊與一般”都可以有很好的體驗和揭示.

5.“有序”的教學

大家都知道有序數對的“有序”是教學重點，但教學實踐中講解“有序”的有效性往往出現偏差.在觀察到的課堂中與文[1]有相似的教學設計：請坐在(3，4)位置上的同學舉手示意，結果有兩個人舉手，因為沒有明確規定是先數行還是先數列，從而強調出“有序”.從表面上看好像沒什么問題，先數行后數列不同于先數列后數行，說明有序，但要是這樣講解的話，給學生的感覺是“有序即此(3，4)非彼(3，4)”，明顯不合有序數對的本意，其實，先數行還是先數列是問題中的規定，而我們往往是在某規定下再來討論數學問題，有序數對的“有序”的實質是(3，4)≠(4，3)，我們要離開3、4的幾行幾列具體含義而抽象出數學概念“有序數對”，因此，講解有序很簡單，規定先數列后數行，(3，4)與(4，3)位置上的同學不同.另外，如果列是用數Ⅰ，Ⅱ，…，行是用數1，2，…來表示，這樣(Ⅱ,3)與(3,Ⅱ)就可以表示同一個位置，這樣的(Ⅱ,3)是數對，但不是有序數對.

6.同型練習題題量的把握

為了加強對有序數對概念的理解，強化變式訓練，是應該的，但同型練習題題量要有一個度，前面介紹的教學設計中的練習，同一題中找4—7個位置的數對，第1—4道題雖然情景有些變，但情境沒有變，都是“垂直”、“找位置或位置的有序數對”；文[2]在練習鞏固、深化提高環節中，若(1，3)表示第一列第三排，要求在網格圖中用彩筆把(5，2)、(4，3)、(3，4)、(2，5)、(2，6)、(3，7)、(4，7)、(5，6)、(6，7)、(7，7)、(8，6)、(8，5)、(7，4)、(6，3)共十四個位置的圓形涂上顏色，題量是不是有點多呢，是不是可以省出時間去學習或思考別的問題.

7.上述圖6這道題的教學

求圖6中小華從A走到B的最短路線這道題是一道好題，是培養學生能力的好題，是這一課時能夠呈現精彩的地方，但是在教學實際中幾乎沒有看到精彩，也許是前面花時間太多的原因，到這兒沒多少時間了，只能草草收場.作者觀察到有兩種表現：第一、學生(或小組)先練習，然后學生(代表)報告結果，在同學們的共同努力下一般是能夠找到答案的，老師給予表揚.第二、教師講解，講解分類去找的方法，指出長方形關于對角線對稱，因此只要在對角線一邊去找最短路線.對于分類討論方法，分類標準的制定與方法的實施不是一個簡單的教學問題，需要長期的具體的教學與指導，學生才能掌握.對這題的教學單是學生練習，給出答案是不夠的，教師應該講解分類去找的方法，做到不重復，不遺漏；對于表現二，不能說長方形關于對角線對稱，軸對稱是數學的精確概念，與生活中的俗語有區別，長方形關于對角線是不對稱的，只是關于中心對稱.

數學教學的備課，基礎問題是備兩頭，即備學生、備教材.備學生要掌握學生的認知基礎，備教材要吃透教材.教學有法，需認真掌握.