命制數列結構不良多選題初探*

福建省漳州市第一外國語學校(漳州八中) (363000) 馮精華

2019年教育部已明確提出立足全面發展育人目標，構建高考考查內容體系.新時期數學高考內容改革的重要特征是由能力立意轉變到素養導向，其題型變化主要體現在試卷中增加了多選題和結構不良問題.區分度更好的多選題,為不同層次學生都提供了更為廣闊的發揮空間.而結構不良問題是指那些初始狀態、目標狀態、解決方法至少有一項不清晰的問題.這類問題的五個主要特征是：問題條件部分缺失或冗余；問題目標界定不明確；具有多種解決方法、途徑；具有多種評價解決方法的標準；所涉及的概念、規則和原理不明確等.

學生解答多選題時，通常無法再使用“排除法”、“特殊法”等等這些單選題常用的解題技巧.還有，學生早已習慣了解答結構良好問題，對于題目條件和結論不確定性的結構不良問題常常表現出不適應,無法清楚找出解決問題的切入點.本文基于結構不良問題的上述五個特征，對數列結構不良的多選題進行分類命制與探析，請同仁們斧正.

一、問題條件部分缺失或冗余

對于條件部分缺失的問題，需要學生結合題意選擇或創設問題的條件，從而達到問題的目標狀態，因此其答案通常具備多樣性和規律性.而條件冗余的問題通常表現為初始信息過多，需要根據目標狀態利用相關信息，對條件判斷與篩選，進行合理搭配，進而解決問題.

例1 已知等比數列{an}的公比為q，前4項和為a1+14，若要使a2,a3+1,a4成等差數列，則需添加的條件可能是( ).

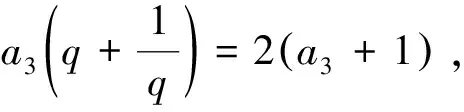
例2 已知數列{an}滿足an+1=3an+4，為求出數列{an}的通項公式an，下列條件多余的是( ).

A.a1=1 B.an+1+2=3(an+2)

C.an+1+3an-1=4anD.an+1-an=2×3n

剖析：由已知得數列{an}僅滿足一個遞推關系，還需加一個條件來確定該數列，若a1=1，則可求出數列{an}的通項公式an，因而A選項不多余；由an+1=3an+4可得an+1+2=3(an+2)，說明B選項多余；由an+1=3an+4，可得an=3an-1+4，兩式相減得an+1-an=3an-3an-1，即an+1+3an-1=4an，說明C選項多余；令bn=an+1-an，則bn=3bn-1(n≥2)，故{bn}是以b1=a2-a1=6為首項，3為公比的等比數列，所以bn=6×3n-1=2×3n，說明D選項多余.故選B、C、D.

對這類問題的命制，需要教師具備較強的發散性思維，從思維的不同方向、不同角度去推理，從問題的側面或反面去命制問題，體現思維的廣闊性和問題的多樣性.

二、問題目標界定不明確

對于目標界定不明確的問題，需要學生從題目中分析諸多現象，提煉有用的數學信息，設計問題的目標，并將所學的數學知識和技能遷移其中，以便解答.

例3 為貫徹生態文明思想，我市準備用幾年的時間把正在使用的1萬輛燃油公交車更換為電力型和混合動力型機動車，并先在年初投入128輛電力型公交車和400輛混合動力型公交車.并計劃以后每年電力型公交車點的投入是上一年的1.5倍，而混合動力車的投入每年比上一年多投a輛.若我市準備在7年內讓燃油車全部“下崗”，則a的可能取值是( ).

A.145 B.146 C.147 D.148

剖析：本題中的“7年內”是一個不明確的目標，可能是第5年，第6年等等.通過分析，學生需要提煉出這樣的信息：當a取最小整數時，該市的燃油車公交車經過7年剛好完成了全部更換.其解答如下：

正由于目標的不確定，學生容易感到“前途迷茫”，信心不足，也就更需要強大的心理素質和良好的數學品質.因此，命題者要注意問題難度的設置，建議剛開始時從真實的生活情境出發，著眼于中低難度的問題，等時機成熟，再適當增加難度.

三、具有多種解決方法、途徑

具有多種解決方法、途徑的結構不良問題，通常與所學知識無過多關系，總是沒有固有、統一的解決辦法，更能考驗學生的主動思維.

例4 設公差為d的等差數列{an}，其前n項和為Sn，則下列方法中能推導出等差數列前n項和公式的是( ).

剖析：選A、B、C，解析略.本題既根植于課本，又高于課本；既與課程標準和教材內容緊密聯系，以教材中的基本問題為依托，又將教學內容轉化為符合學科邏輯的結構不良問題.

學生在解題過程中，往往會難以找到連接問題初始狀態和目標狀態的有效方法，從而沒能關聯到有用條件.這就需要學生合理猜想、大膽的推測，發現和創造一個“新”的問題解決方案，這種創造性的學習調動了學生的主動思維，促進了學生問題解決能力的發展.

四、具有多種評價解決方法的標準

此類問題的解決方案通常沒有統一的答案，解決方法顯得靈活且無序，需要命題者應用多種評價標準加以保障.有效且合理的評價能促進學生突破思維障礙、超越問題本身，還能引導學生進行深度思考，培養高階思維.

例5 觀察下列數表

1

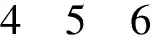
以下解釋正確的是( ).

A.第n(n≥3)行共有n個數，各數排列成公差為1的等差數列；

B.第n(n≥2)行第1個數等于第n-1行最后一個數加1；

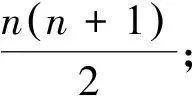
D.98在第14行第8列.

剖析：選A、B、C.此類問題較多體現在解答題，而以多選題的題型出現的較少.但由于多選題“全部選對的得5分，選對但不全的得3分，有選錯的得0分”這一評價方式，該類問題也能具備良好的區分度.

命制此類問題時，教師首先要根據考查意圖，在選題時貼近學生的知識水平、生活經驗，使學生能充分地理解題意，再考慮剔除偏離目標的細枝末節，保留關鍵性事實，對試題進行適當的處理.

五、涉及的概念、規則和原理未明確

這類結構不良問題通常是不以考察某一具體知識為主要目的，而是以思維訓練的形式呈現，以考查學生思維的靈活性與開闊性，主要表現在所指向的概念、規則等不明確，無法利用固定的辦法和途徑去解決，需要學生嘗試或創造各種方法以達到目標.

例6 十三世紀意大利著名數學家列昂納多·斐波那契在研究兔子繁殖問題時，發現有這樣一列數：1，1，2，3，5，… 該列數從第三項起，每個數等于它前面兩個數的和，后來人們把這樣的一列數組成的數列{an}稱為“斐波那契數列”，記Sn為數列{an}的前n項和，則下列結論正確的是( ).

A.a10=65 B.an+1=an+2-an

C.a1+a3+a5+…+a2019=a2020

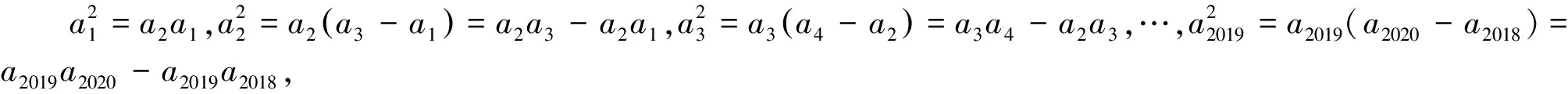
上述問題由于現實情境，沒有直接表述出固定的定理、規則或常識，只是隱含了關鍵的解決信息，這需要學生嘗試或創造各種方法來解決問題.

結構不良問題給學生提供了更為廣闊的思維空間，有利于學生數學能力的培養及數學核心素養的形成.希望同仁們能重視數學結構不良問題的命制，以期更好地培養學生的數學思維品質.值得一提的是，有些數學結構不良問題可能包含上述多種特征，在區分其結構類型時，需要根據問題最為顯著的特征來判斷，而其解決的方式方法，更應具體問題具體分析.