基于主應力旋轉的黏性填土擋墻土壓力

王恒利，鄒正盛，劉京敏，王新宇

（1.河南理工大學土木工程學院，河南 焦作 454003；2.河南省地下空間開發及誘發災變防治國際聯合實驗室，河南 焦作 454003；3.河南省地下工程與災變防控重點實驗室；河南 焦作 454003；4.中國地質工程集團有限公司，北京 100093）

眾所周知，擋墻墻背粗糙，黏性土擋墻墻土界面存在一定的摩擦。對于這種情況，經典朗肯土壓力理論不再適用。為了使理論計算結果更接近于實際，眾多學者探索考慮墻土摩擦作用的土壓力計算。

考慮墻土摩擦進行黏性土土壓力計算時，大多為基于經典理論的修正方法。早期的方法有：等值內摩擦角法、楔體試算法、內壓力法、圖解法等[1?3]。后來，一些學者在庫倫土壓力理論的基礎上進行了改進，取得了一系列進展。朱桐浩等[4]在庫侖理論平面滑裂面假設條件下，從土體的極限平衡條件出發，由滑動楔體的極限平狀態，導出考慮墻土摩擦的黏性土主動土壓力計算式。趙恒惠[5]基于庫倫土壓力理論，將墻土之間摩擦角和墻土之間的黏結力用折減土體內摩擦角和黏結力表示，推導了重力式擋墻土壓力計算式。顧慰慈[6]假定滑裂面為平面，導出考慮墻土摩擦的黏性土主動土壓力的庫侖解。羅紹軍[7]基于庫倫平面滑裂面假定，考慮滑裂面黏聚力作用，通過力矢多邊形，建立了黏性土主動和被動土壓力計算式。盧廷浩[8]應用平面滑裂面假定，考慮墻土摩擦及黏結力以及填土表面裂縫和超載的影響，推導了擋墻的主動土壓力計算式。李巨文等[9]在文獻[5]的基礎上，給出了距墻頂一定距離均布荷載作用下的主動土壓力計算式。胡曉軍[10?11]基于庫侖理論的平面滑裂面假設，先后建立了考慮墻土接觸面上黏結力與摩擦力作用的主被動土壓力計算式。彭明祥[12?13]認為極限土壓力是由墻后塑性土體產生，假定塑性區平面滑裂面，建立了考慮墻土摩擦及墻土界面黏結力作用的擋墻土主動土壓力計算式。楊敏等[14]基于平面滑裂面假定，結合微分層解析法和圖解法，推導了考慮墻土摩擦及黏結力作用的土壓力計算公式。曹雄等[15]在文獻[8]的基礎上，應用力的矢量多邊形法推導了考慮墻土摩擦及黏結力作用的主被動土壓力計算式。柯才桐等[16]基于庫侖土壓力理論假設，從滑動楔體極限平衡狀態時力的靜力平衡條件出發，推導出不同分布模式條形荷載作用下考慮墻土摩擦和墻土之間黏結力的主動土壓力計算式；后來，又采用斜向條分法，推導了一般條件下擋墻土壓力強度的表達式[17]。胡衛東等[18]基于平面滑裂面假定，對極限平衡狀態的墻后土楔體進行靜力平衡分析，考慮墻土界面摩擦與黏結力、填土的黏聚力影響，建立了有限土體主動土壓力計算方法。陳建功等[19]從墻后滑楔體整體靜力平衡方程出發，采用整體極限變分法對土壓力進行求解，建立了考慮墻土摩擦的黏性土擋墻土壓力計算方法。

事實上，對于朗肯擋墻，當墻背與其后土體之間存在摩擦時，墻后土體會產生非均勻應力場，墻背附近土體由于墻土摩擦產生的剪切力而使土體單元主應力方向發生偏轉，而墻背稍遠處土中應力場仍符合朗肯土壓力條件。針對墻背面土體主應力偏轉這一事實，Lancellotta[20]基于塑性下限定理，采用主應力旋轉辦法，建立了考慮墻土摩擦的土體極限狀態下無黏性土擋墻的主被動土壓力計算方法；后來，又進一步給出了地震條件下的無黏性土的主被動土壓力計算公式[21]。

然而，目前針對黏性土條件下的土壓力計算研究較少。本文擬采用主應力旋轉處理方法，考慮黏性土中的黏聚力作用，推導考慮墻土摩擦和黏結力作用的黏性土主動土壓力和被動土壓力的計算公式；同時，將計算結果和現有相關方法進行對比，分析墻土摩擦角和土體內摩擦角對黏性土擋墻土土壓力的影響。

1 被動土壓力計算解析

對于被動狀態的朗肯擋墻，由于墻土摩擦作用，墻后土體將分別處于兩種應力狀態區域：墻后相對遠處土體的大小主應力分別為水平應力和豎向自重應力；近墻土體由于墻土摩擦和黏結力作用，水平應力和豎向自重應力不再是大小主應力，主應力軸向墻外發生一定程度的偏移。無疑，這兩種應力狀態間存在1條公共線（即界線），如圖1所示。

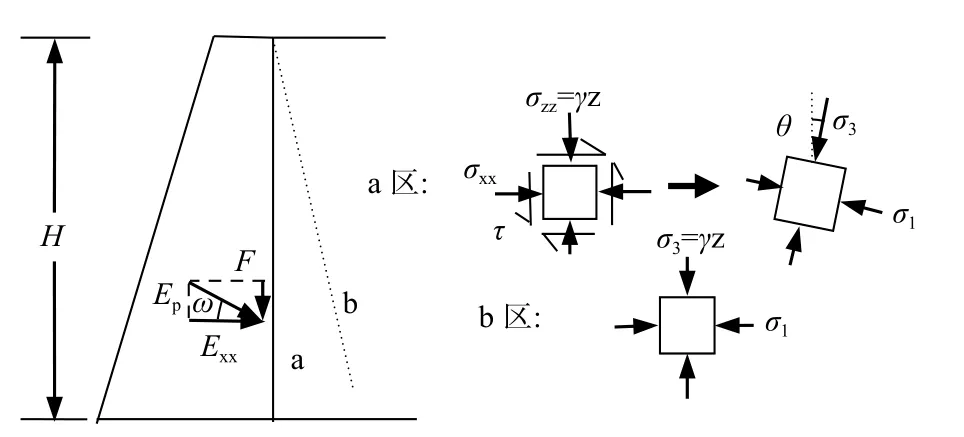
圖1 被動極限狀態土體單元應力圖Fig.1 Stress of soil element under the passive limit state

取墻背和墻后土體單元進行應力分析。對墻后土中兩種應力狀態進行推算，則在分界線上應力不一致（圖2）。圖2中，未發生偏轉的莫爾圓與包線在T處相切，偏轉后的莫爾圓與偏轉前的莫爾圓交點為X。對于黏性土，由于黏聚力不為零，可將τ軸左移l（l=ccotφ），得到坐標原點為（0,0）的新坐標系，s'=s+l，σ'xx=σxx+l。通過對三角形ABX應用正弦定理，可以得到：

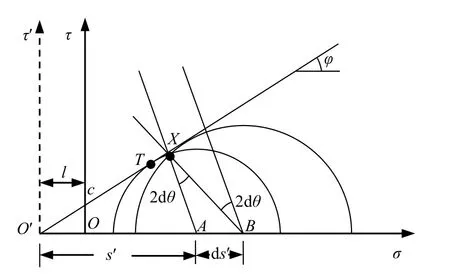
圖2 應力圓心偏移圖Fig.2 Diagram showing the stress center deviation

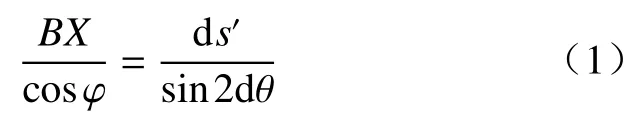
假設應力圓產生1個小轉動2dθ。當ds'→0時，sinθ≌θ，公共點X→T，則BX≌AX。此時式（1）變為：

則：

式中：θ—主應力方向的旋轉角；

φ—填土內摩擦角；

s'—調整后的莫爾圓圓心橫坐標。

繪制被動擋墻墻背及墻后土體摩爾應力圓（圖3），其中墻后土體應力圓2主應力方向未發生偏轉，圓心橫坐標為s′2。假定主應力方向的偏轉為有限值θ，得到墻背土體應力圓1，圓1的圓心橫坐標為s′1。顯然，圓2的偏轉角為0，圓1的偏轉角為θ。對式（3）積分：

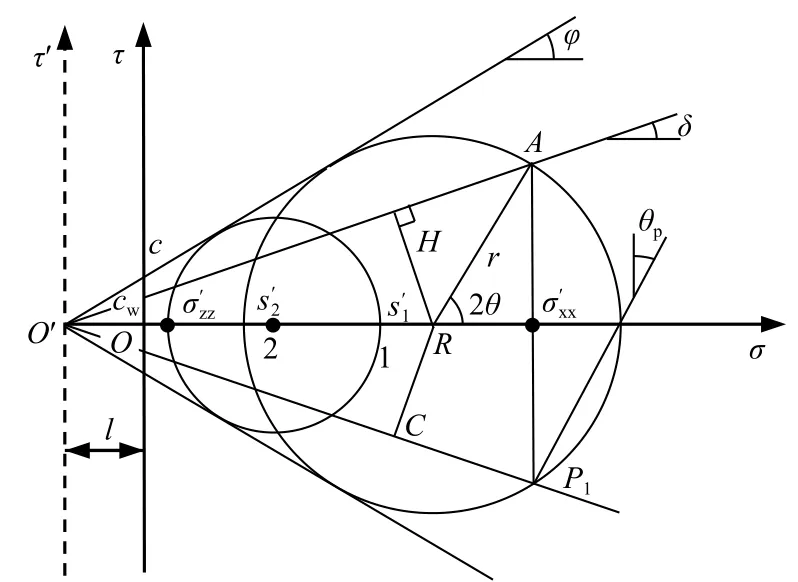
圖3 被動土壓力應力圓Fig.3 Passive earth pressure stress circle

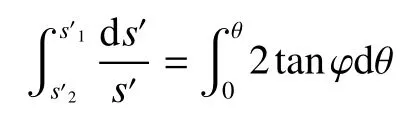
得：

在主應力方向偏轉后的應力圓1中（圖3）：

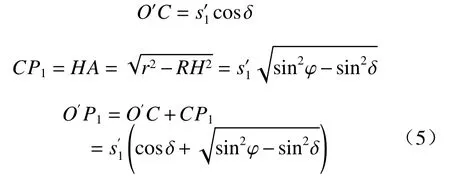
式中：δ—墻背與填土間的摩擦角。

又由于

且圓2之中主應力方向未發生偏轉，即：

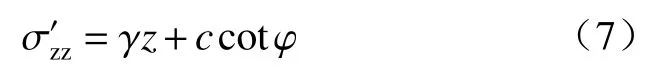
故：

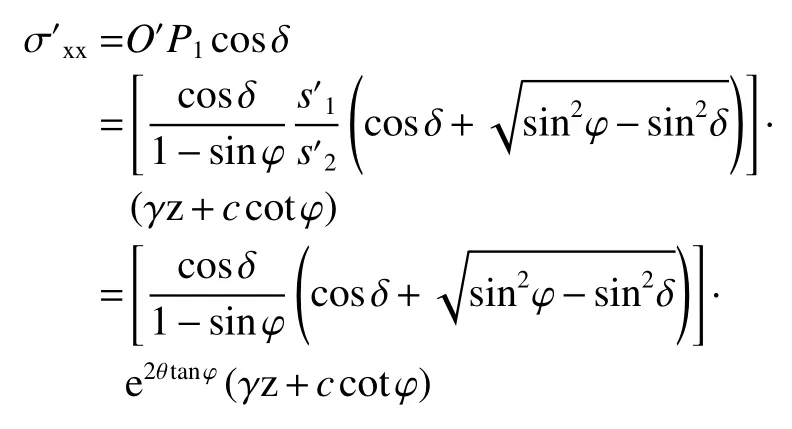
墻背土體單元水平應力為：

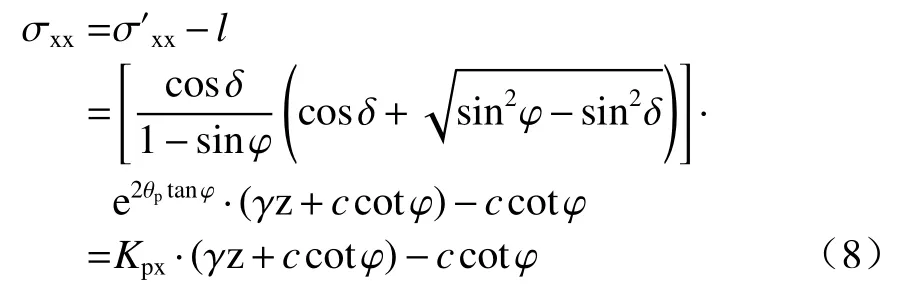
式中：

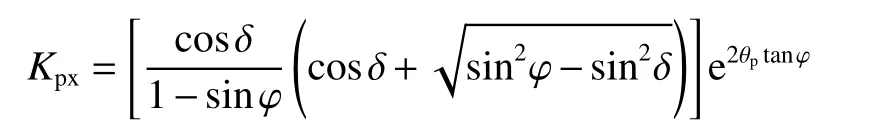
墻背土體單元剪應力：

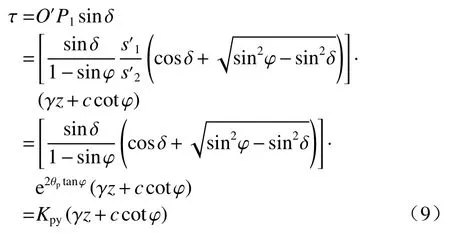
式中：

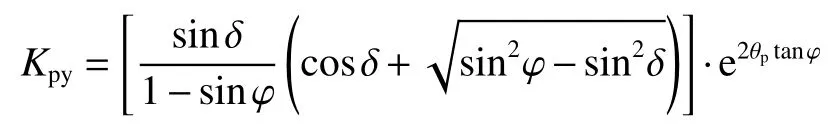
則作用在擋土墻上的被動土壓力強度為：

墻背切向力：

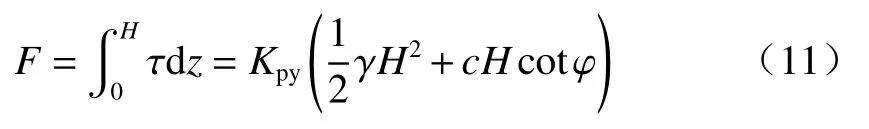
墻背水平力：

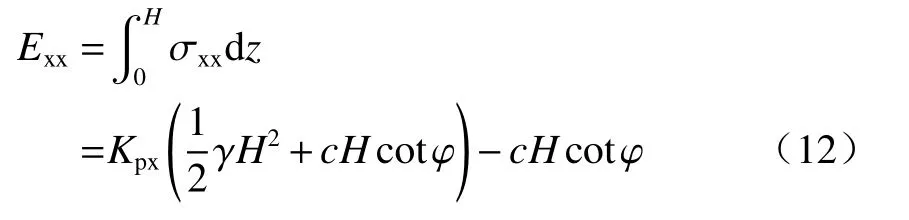
則黏性土擋土墻被動土壓力為：

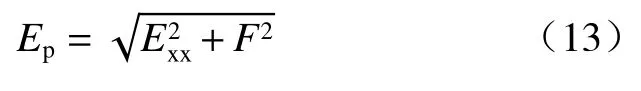
被動土壓力與墻背法線之間夾角：

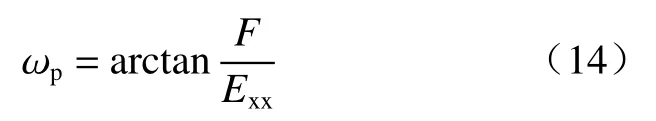
由圖3中的圓1，有：

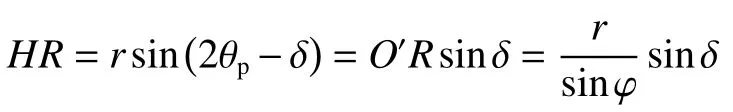
則墻后土體主應力偏轉角θp為：

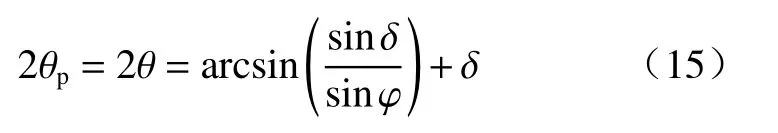
由圖3可知，墻土界面黏結力cw與墻土界面摩擦角δ、填土黏聚力c、內摩擦角φ存在如下關系：

若墻背光滑（δ=0），則θp=0，cw=0，式（13）退化為：

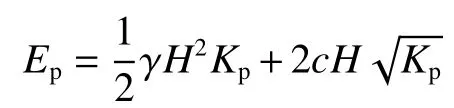
這意味著，若不考慮墻土摩擦角，被動土壓力計算式與朗肯被動土壓力公式相等。

2 主動土壓力計算解析

對于主動土壓力情形，墻后土體應力狀態如圖4所示。同樣，取墻背和墻后土體單元進行分析，則主動擋墻墻背及墻后土體摩爾應力圓如圖5所示。其中，主動土壓力應力圓1為墻后土體單元應力圓，圓心橫坐標為s′1，主應力方向未發生偏轉。墻背土體應力圓2，主應力方向偏轉角為θ。同理有：

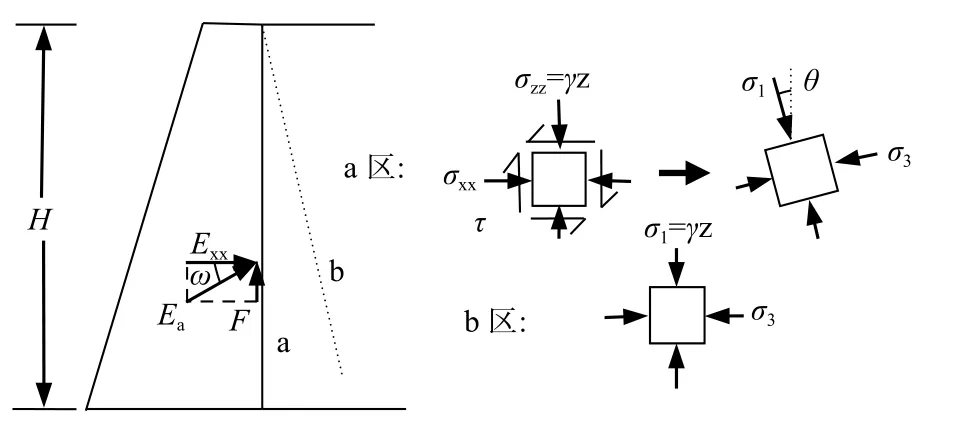
圖4 主動極限狀態土體單元應力圖Fig.4 Stress of soil element under the active limit state

由圖5可得：

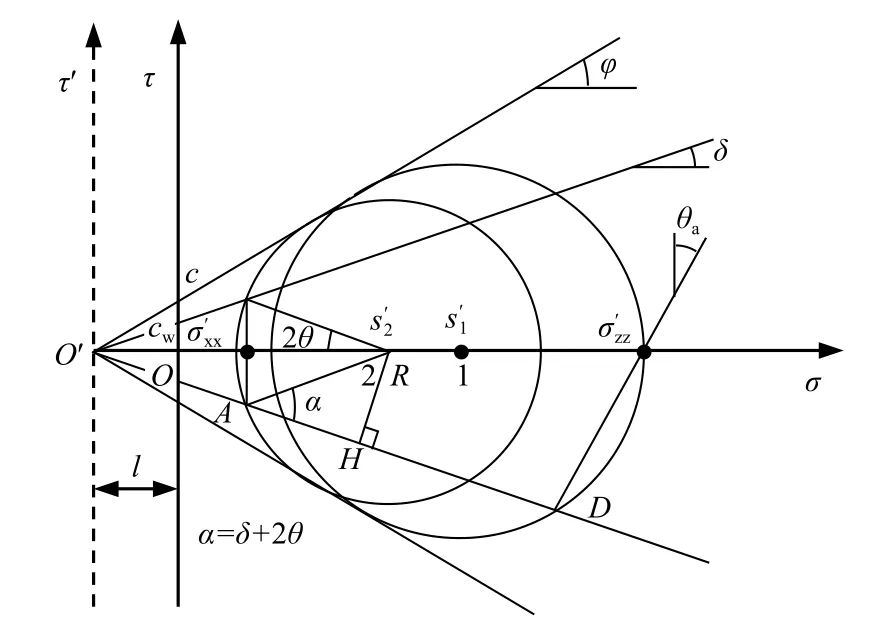
圖5 主動土壓力應力圓Fig.5 Active earth pressure stress circle

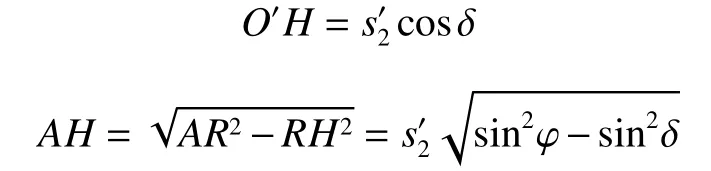
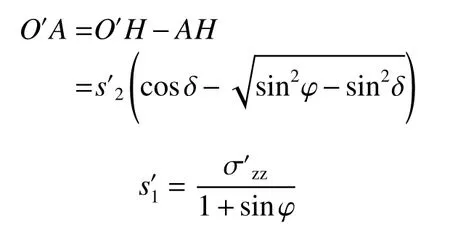
由于圓1之中主應力方向未發生偏轉，則：

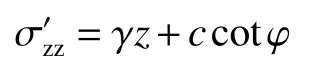
可得：

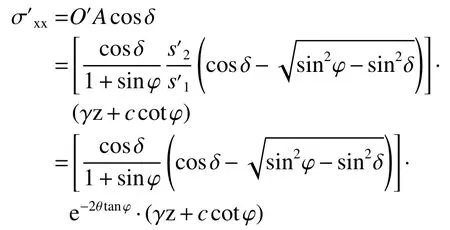
墻背土體單元水平應力：

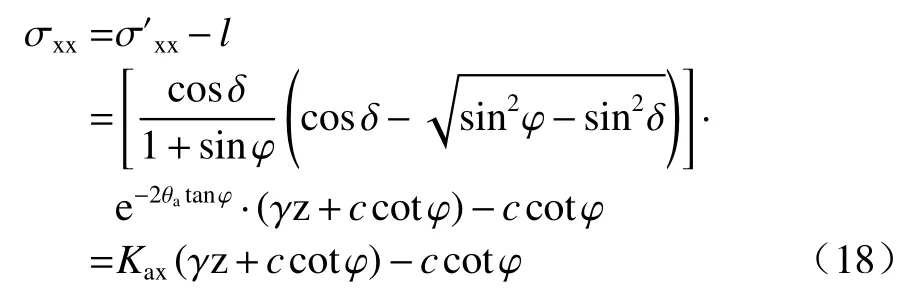
其中：

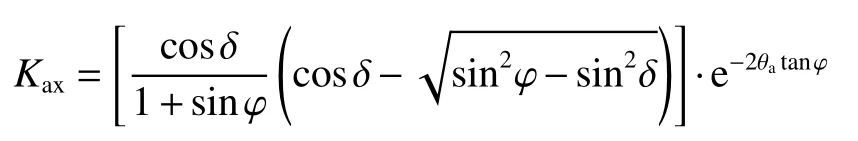
墻背土體單元剪應力：

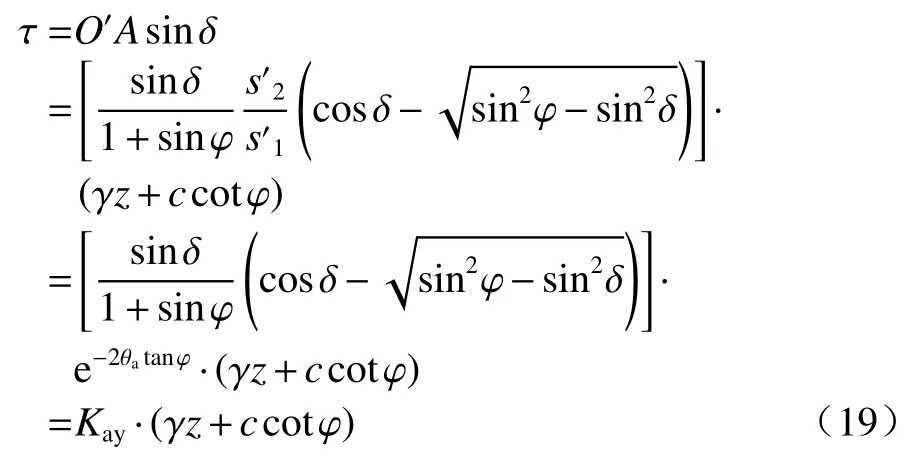
式中：

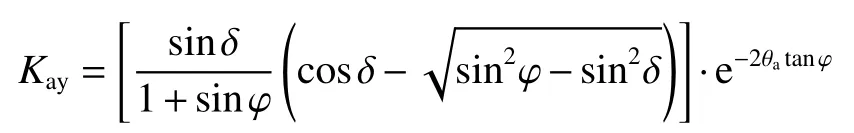
從而，作用在擋土墻上的主動土壓力強度為：

拉應力區臨界深度為：

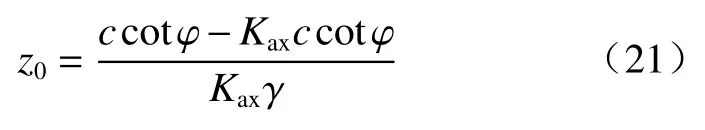
則：

將開裂土層深度范圍內的土等效成均布荷載作用：

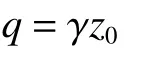
墻背切向力：

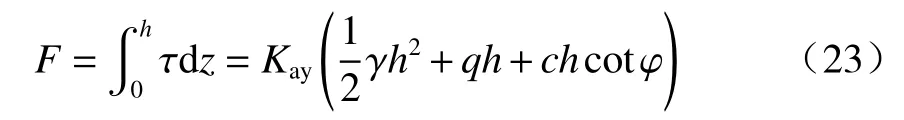
墻背水平力：

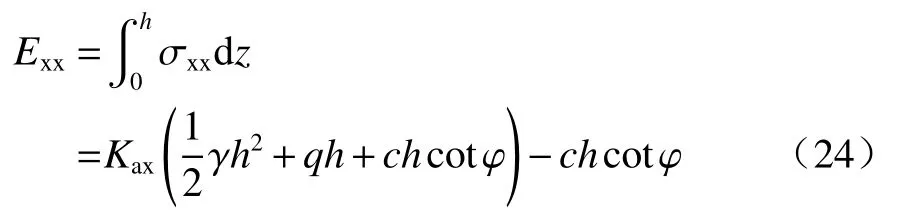
作用在墻背的主動土壓力為：

主動土壓力與墻背法線之間夾角：

同理可得墻背土體主應力偏轉角θa為：

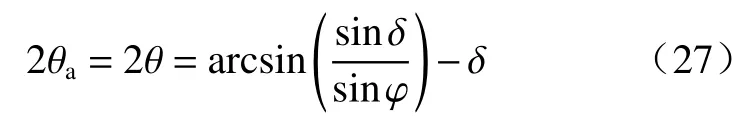
由圖（5）可得墻土界面黏結力cw為：

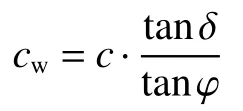
若墻背光滑（δ= 0），則有θa=0，cw=0，式（25）退化為：

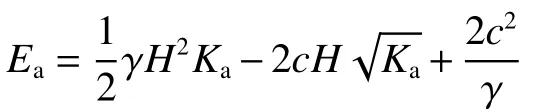
顯然，若不考慮墻土摩擦角，主動土壓力與朗肯主動土壓力相同。

3 基于算例的對比分析

3.1 黏性填土擋土墻土壓力計算的代表方法

（1）朗肯土壓力理論。朗肯土壓力理論是經典的黏性土土壓力計算理論，是根據半空間的應力狀態和土的極限平衡條件而得到的土壓力計算方法。但朗肯理論假定擋土墻墻背光滑，忽略了擋土墻墻背與土體之間的摩擦和黏結力作用。

（2）盧廷浩法[8]。該法基于庫倫理論平面滑裂面假定，考慮擋墻墻背與黏性填土的摩擦及黏結力、填土表面的裂縫及荷載以及滑裂面黏聚力的影響，由滑動楔體力矢圖推導出主動土壓力公式。以編程試算法得到滑裂面傾角的精確值求得主動土壓力精確解。

（3）胡曉軍法[11]。該法基于庫倫理論平面滑裂面假定，考慮填土的黏聚力、墻土界面的摩擦力和黏結力，通過力矢多邊形建立均布荷載作用下一般形式的黏性土擋土墻被動土壓力計算公式。

（4）柯才桐法[17]。該法同樣基于庫倫理論平面滑裂面假定，但采用斜向條分法，考慮墻后黏性填土、墻土界面的摩擦力和黏結力以及均布荷載作用，通過土條靜力分析，給出了一般形式的黏性土擋墻主動和被動土壓力計算公式，并基于公式的特殊處理給出了滑裂角計算式。

3.2 對比分析

運用朗肯理論、盧廷浩法、胡曉軍法、柯才桐法以及本文方法對以下2個算例進行計算并對比。

算例1：某擋墻墻高H=10 m，，墻背豎直，墻后填土水平，墻后填土表面無超載。填土參數為γ=18.6 kN/m3，φ=24°，其它有關參數及計算結果見表1，其中取cw=c·tanδ/tanφ。

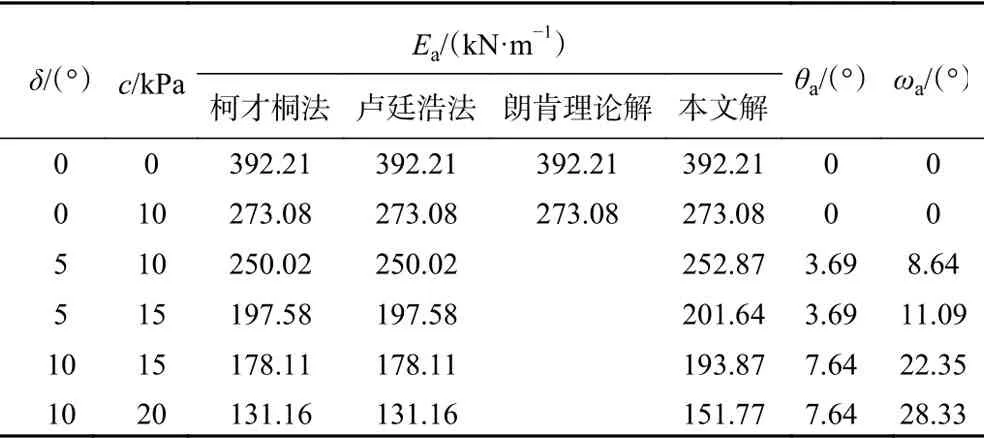
表1 主動土壓力算例Table 1 Example for the active earth pressure

算例2：某擋土墻墻高H=8 m，填土參數為γ=18.6 kN/m3，φ=20°，墻背豎直，墻后填土水平，無超載作用，其它有關參數及計算結果列于表2，其中取cw=c·tanδ/tanφ。

由表1和表2可以看出，對于符合朗肯假設條件的情況，本文方法所得主被動土壓力與朗肯理論的結果相同。對于考慮墻土摩擦和黏結力的黏性土擋墻主動土壓力，本文方法所得結果大于其他學者的結果。對于考慮墻土摩擦和黏結力的黏性土擋墻被動土壓力，本文方法所得結果小于其他學者的計算結果。本文方法主動和被動土壓力計算結果與其他學者主動和被動土壓力計算結果的差值變化規律一致，均隨著δ、c的增大而增大。

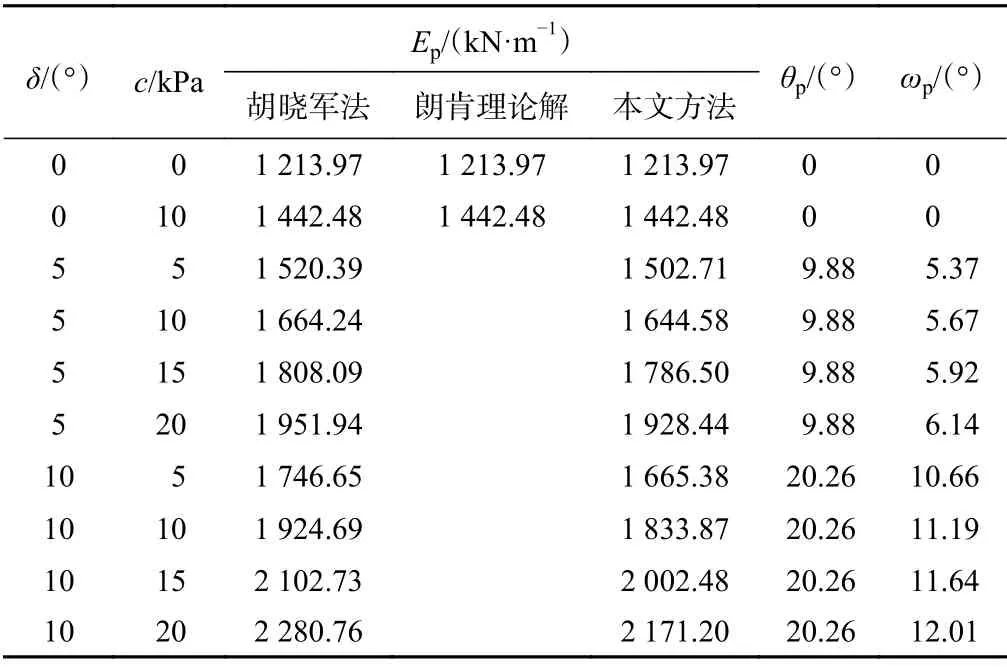
表2 被動土壓力算例Table 2 Example for the passive earth pressure

表1和表2還表明，由于本文方法考慮了墻土界面黏結力作用，墻土界面的黏結力包含在土壓力切向分量F中，使得土壓力與墻背法線夾角ω大于摩擦角δ，且隨著摩擦角δ、黏聚力c的增大而增大。墻土摩擦角越大，墻背土體主應力偏轉越大，本文方法所得結果與他人結果相差也越大。然而當主應力旋轉角θ=20°時sinθ≈θ仍成立，兩者的誤差只有0.007。顯然，因考慮了墻后土體主應力偏轉的事實，本文方法所得結果更客觀、計算式更為簡明易用。

4 參數敏感性分析

設擋墻高H=4 m，墻背豎直，墻后土體表面水平且無超載，填土γ=20 kN/m3，c=12 kPa。取φ=5°～35°，δ=（0～0.7）φ，分析δ、φ對土壓力的影響（圖6、圖7）。圖6和圖7分別反映作用在擋墻墻背的主被動土壓力隨δ和φ的變化情況。對于主動土壓力，當φ<10°時，主動土壓力隨δ、δ/φ增大不斷減小，且減小的速度在逐漸減緩；當φ≥10°時，主動土壓力隨δ、δ/φ增大先減小后增大，但總體變化不大；當δ不變時，主動土壓力隨φ增大不斷減小，且減小的速度在逐漸減緩。被動土壓力則隨δ、φ、δ/φ的增大不斷增大，且增大的速度在逐漸加快。主動土壓力隨δ值增大不斷減小，但總體變化不大。φ值對主被動土壓力影響均較δ顯著。

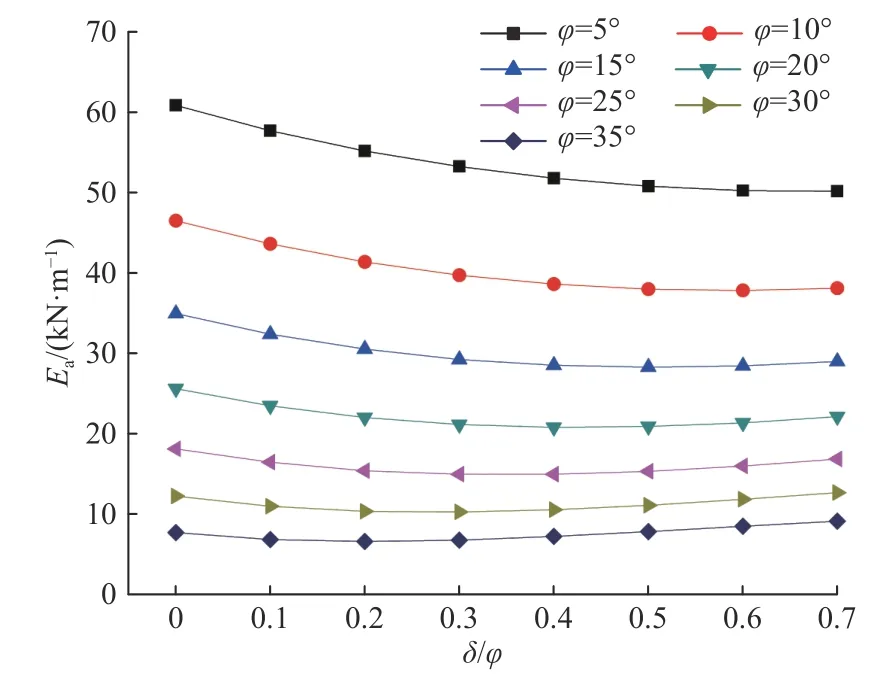
圖6 主動土壓力隨δ/φ的變化Fig.6 Change of the active earth pressure with δ/φ

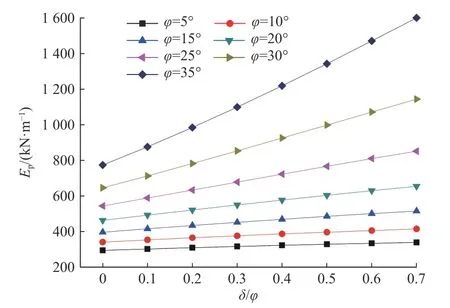
圖7 被動土壓力隨δ/φ的變化Fig.7 Change of the passive earth pressure with δ/φ

5 結論

（1）采用主應力旋轉處理墻后土體主應力偏轉現象，推導出考慮墻土摩擦和黏結力作用的黏性土擋墻土壓力計算式，朗肯土壓力公式只是新方法公式的特例。由于墻土界面黏結力作用，土壓力與墻背法線的夾角ω大于摩擦角δ。

（2）當黏性土內摩擦角φ較小時，墻土界面黏結力影響較小，隨著墻土摩擦角δ的增大，主動土壓力不斷減小，且減小的速度逐漸減緩；當φ值較大時，隨著墻土摩擦角δ的增大，墻土界面黏結力加強，主動土壓力先減小后增大。被動土壓力隨著墻土摩擦角δ的增大不斷增大，且增大的速度在逐漸加快。隨φ值增大，主動土壓力減小且減小的速率在逐漸減緩，被動土壓力增大且增大的速率在逐漸加大。φ值的影響比δ值更明顯。

（3）對于主動土壓力，本文方法所得結果大于其他學者的結果。對于被動土壓力，本文方法所得結果小于其他學者的計算結果。本文方法主被動土壓力計算結果與其他學者主被動土壓力計算結果的差值變化規律一致，均隨著δ、c的增大而增大。本文方法考慮了墻后土體主應力偏轉的事實，計算結果更客觀。