基于深度學習的盾構豎向姿態組合預測

李增良

(中鐵二十局集團有限公司，陜西 西安 710016)

0 引言

盾構姿態控制是盾構施工過程中重要的環節之一。傳統的被動式控制方式具有一定的滯后性，很難在施工過程中實現及時有效的控制。因此，實現盾構姿態的主動控制成為盾構施工過程中施工人員關注的核心問題之一。

盾構姿態的精準預測，能夠為盾構姿態主動控制提供決策依據。近年來，隨著計算機水平的不斷提高，相關的機器學習、人工智能方法在盾構姿態預測方面得到了廣泛應用。不同于力學建模[1-2]、模糊理論[3-4]等盾構姿態預測方法，機器學習方法主要是以實際施工數據為驅動，在確定模型輸入、輸出變量的基礎上實現對盾構姿態的預測。高兵[5]基于專家系統、知識推理實現了盾構姿態的實時預測。李英偉等[6]、張愛軍[7]分別基于BP神經網絡建立了角礫地層盾構管片位姿和上軟下硬地層盾構豎向位姿預測模型。陳昱竹[8]構建了基于XGBoost-SVR的盾構位姿偏差預測模型。

由于淺層神經網絡對于信息的處理存在一定的局限性，研究者們開始逐步探索深層神經網絡(深度學習技術)的應用。孔憲光等[9]基于深度學習技術，依托寧波地鐵實際盾構施工數據構建了相應的位姿預測模型，該預測模型表現出較高的預測精度和效率。Zhou等[10]在基于小波神經網絡對盾構姿態數據進行降噪處理的基礎上，構建了基于CNN-LSTM的混合深度學習盾構位姿預測框架，為盾構姿態預測提供了新的思路。

盾構掘進姿態數據具有隨時間不斷演進變化的特點，其相應的姿態預測問題屬于典型的時間序列預測問題。由于盾構姿態數據的演化規律復雜，且呈現非線性，通過力學建模、公式推導的方式研究其變化規律難度較大。本文基于上述已有的研究，采用深度學習的方式對盾構姿態進行建模預測。考慮到單一預測模型預測精度不高的問題，采用長短期記憶(long short term memory，LSTM)神經網絡算法和支持向量回歸(support vector regression,SVR)算法分別構建盾構姿態預測模型，并基于最優組合賦權的方式對二者的預測結果進行融合，以期能夠實現較為準確的預測。

1 理論基礎

1.1 長短期記憶神經網絡

對于時間序列數據的預測問題，傳統的淺層神經網絡無法將當前時刻的信息與過去結合起來，很難實現精準預測。因此，一系列深度學習算法應運而生。循環神經網絡可以有效實現過去、現在和將來的融合，是解決時間序列預測問題的“利器”。為進一步解決循環神經網絡在進行長時間序列預測時出現的梯度爆炸和衰減問題，文獻[11]提出了長短期記憶神經網絡方法，其能夠對過去信息進行自動化取舍，預測精度較高，在風電工程[12]、汽車工業工程[13]等多個領域得以廣泛應用。LSTM層通過引入門機制(輸入門、輸出門和遺忘門)來實現對過去信息的選擇性保留和去除，相應的結構圖如圖1所示。相應的計算公式為

(1)

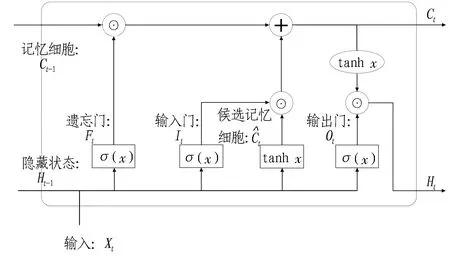
圖1 LSTM結構圖Fig.1 Principle diagram of LSTM

1.2 支持向量回歸算法

支持向量回歸算法[14]適用于解決小樣本數據情況下的預測問題。該算法實現預測的方式主要是通過若干有限個樣本數據去尋找最優超平面，以實現所有樣本點與最優超平面之間的偏差和最小。設1組樣本數據集為{xi,yi}(i=1,2,3,…，n)，xi∈Rn(n維實數集)為輸入量，yi∈R(一維實數集)為輸出量。通過非線性映射關系φ(x)將樣本投射到高維線性空間中，即

f(x)=wφ(x)+b。

(2)

式中w和b為待求解參數。

基于式(1)構建支持向量回歸模型時，需要設定一定的誤差容忍度ε(不敏感損失函數)來提高算法的容錯能力。誤差容忍度設定的基本思路是當模型算法輸出值f(x)(預測值)與真實值Y之偏差在[-ε,ε]時，不計損失，否則將其計入損失。SVR原理如圖2所示。

ζi為實測值與預測值之間的偏差。圖2 SVR原理圖Fig.2 Principle diagram of SVR

通過引入Lagrange函數得到對偶模型并進行求解，可得最終模型解的形式為

(3)

在構建支持向量回歸模型中，相關的核函數類型有線性核函數、多項式核函數、高斯核函數和Sigmoid核函數等，具體如表1所示。

表1 SVR核函數類型Table1 Kernel function type of SVR

2 LSTM-SVR盾構豎向姿態組合預測模型

為實現盾構豎向姿態的精準預測，本文將長短期記憶神經網絡和支持向量回歸算法的優勢進行融合，提出基于LSTM-SVR的盾構豎向姿態組合深度學習預測模型，相應的預測流程如圖3所示。

MRE為平均相對誤差；R2為相關系數。圖3 基于LSTM-SVR的盾構豎向姿態預測流程Fig.3 Vertical posture prediction process of shield based on LSTM-SVR

具體的模型實現步驟如下。

1)收集開展盾構豎向姿態預測的樣本數據。

2)樣本數據預處理，即基于箱線圖法進行數據異常值的識別，基于線性內插的方式對識別出的異常值和樣本數據中的缺失值進行填充；同時，為提高模型運算速度，基于最大最小值法(計算見式4)對預處理之后的樣本數據進行歸一化處理[15]。

(4)

式中：X為歸一化后的數據；x為原始數據；xmin，xmax分別為原始數據的最小值、最大值。

3)確定輸入、輸出變量。在構建預測模型之前，首先需要確定模型的輸入、輸出變量。盾構豎向姿態的智能預測可以分為2類，即多因素的耦合預測和單點的規律性預測。由于多因素耦合預測所要考慮的因素眾多，部分因素的數據成規模采集仍比較困難。而盾構姿態的演化與之前一段時間的姿態狀況具有密不可分的關系，因此，本文采用單點的規律性預測來研究該預測問題，即憑借過去一段時間的姿態數據進行預測。本文采用過去10個時刻的盾構豎向姿態對下一時刻進行預測，即模型的輸入變量為過去10個時刻的姿態數據，輸出變量為下一時刻的姿態數據。為實現樣本數據的最大化利用，采用滑動窗口的方式對樣本數據進行劃分，基于上述確定的輸入、輸出變量，將滑動窗口的寬度m設定為10，滑動步長設定為1。

4)訓練集、測試集劃分。由于本文所采用的LSTM算法在進行當前預測時能夠對過去的信息進行關聯分析，因此，在對該問題進行建模預測時，對測試集和訓練集的劃分是基于滑動窗口劃分后得到的樣本數據，按照時間先后順序以8∶2的比例來劃分訓練集和測試集，即將樣本數據中先產生的80%的數據作為訓練集，后產生的20%的數據作為測試集。

5)模型構建。基于樣本數據分別構建LSTM和SVR盾構豎向姿態預測模型，模型超參數采用交叉驗證網格搜索的方式確定，并基于最優組合賦權法進行模型融合，即采用使LSTM-SVR組合模型調和平均誤差e(見式(5))最小的思想來實現最優組合賦權，通過將其轉化為求解最優化問題來計算。將模型在訓練集上的預測誤差標準設定為平均相對誤差MRE<0.001。當模型的預測結果滿足該標準時，說明模型訓練完畢；反之，則分別調整2個預測模型的超參數，然后對模型進行重新訓練。

(5)

式中：y1，y2分別為LSTM和SVR模型的預測結果；φ1，φ2分別為LSTM和SVR模型預測結果在最終預測結果中所占的比例，0≤φ1≤1，φ1+φ2=1。

6)模型測試。采用訓練好的LSTM-SVR組合預測模型，對測試集數據進行預測，將預測的誤差標準設定為：平均相對誤差MRE<2%且相關系數R2>0.90。MRE和R2的計算分別如式(6)和式(7)所示。MRE越小、R2越大，說明模型預測性能越好。當模型在測試集上的預測結果滿足該標準時，說明模型訓練成功；反之，則返回步驟5)重新調整2個模型的網絡結構和超參數，然后對模型進行重新訓練。

(6)

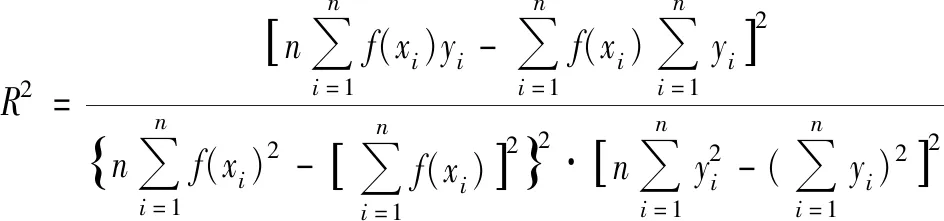
(7)

式(6)—(7)中：f(xi)為預測值；yi為實測值；n為樣本數。

3 實例應用

3.1 盾構豎向姿態數據收集與預處理

為驗證本文所構建的LSTM-SVR盾構豎向姿態組合深度學習預測模型的有效性，以昆明地鐵5號線盾構區間左線為例開展實例應用研究。該區間采用土壓平衡盾構法施工，穿越的地層主要為粉土、泥炭質土、粉砂和粉質黏土。

盾構豎向姿態數據的收集主要是提取盾構PLC系統中實時采集的數據信息。該盾構的數據采集頻率為5 s/次，但由于較高的采集頻率下數據波動較小，對于模型預測沒有實際意義。因此，本文對采集到的數據重新采樣，將其整理成采集頻率為10 min/次的數據信息。取盾構掘進200—240環的豎向姿態數據，經重新采樣后可得樣本數據560組。

為提高模型后續預測的精度和效率，采用第2節中設計的預處理方法對采集到的560組樣本數據進行基于箱線圖法的數據異常值識別、基于線性內插的數據異常值替換和缺失值填充，進而得到較為真實的“去噪”數據，相應的盾構豎向姿態演化趨勢如圖4所示。從圖中可以看出，俯仰角始終大于0°。說明盾構在200—240環掘進時始終處于“抬頭”狀態。為進一步提高建模過程中模型的收斂速度，將樣本數據基于式(4)進行歸一化處理。

3.2 LSTM-SVR組合預測模型的構建

3.2.1 盾構豎向姿態數據收集與處理

本實例所使用的計算機配置和軟件環境為：Intel(R)Core(TM)i5-7200U CPU，16.0 GB內存。系統是Windows10(64位)，程序語言版本為Python 3.7.8，集成開發環境為Anaconda包中的spyder 4.1.4版本，在Keras庫中以Tensorflow為后端實現。

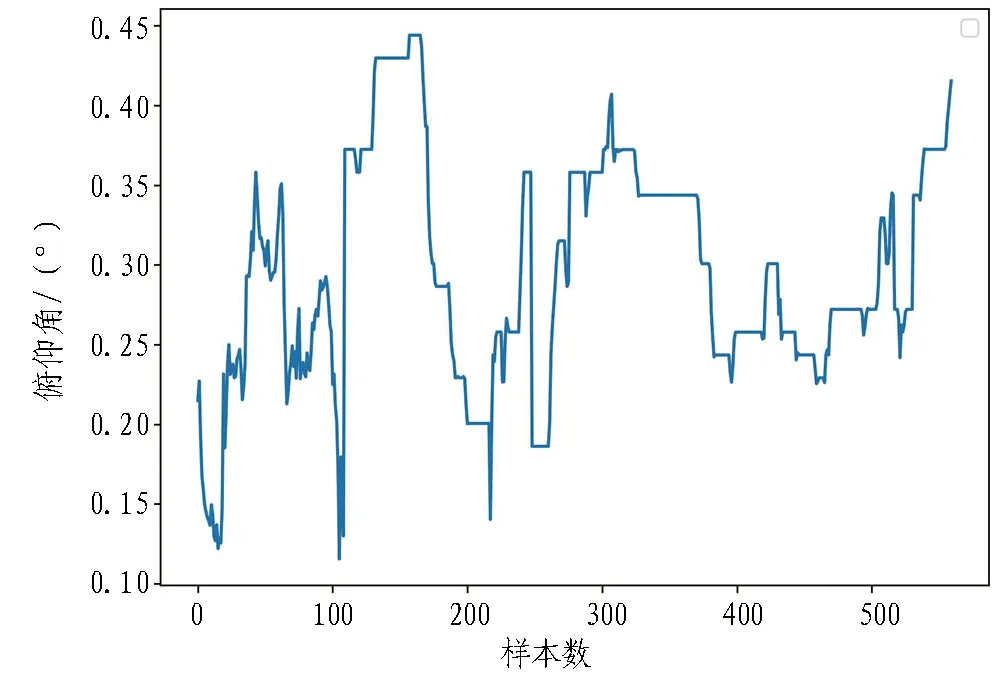
圖4 200—240環盾構豎向姿態演化趨勢圖Fig.4 Shield vertical posture evolution trend of rings 200 to 240

本文在構建盾構豎向姿態預測模型時，將過去10個時刻的姿態數據作為輸入變量，下一時刻的姿態數據作為輸出變量。為了提高樣本數據的利用率，采用第2節中設計的滑動窗口方式進行數據整理，即可得到用于建模訓練的樣本數據550組。

在建模前，將樣本數據按照8∶2的比例進行劃分，即可得到訓練集440組，測試集110組。然后基于440組訓練集數據分別構建LSTM和SVR盾構豎向姿態預測模型。

在構建LSTM模型時，將模型的網絡結構設定為1個輸入層、1個輸出層、3個LSTM隱含層和1個Dense層，比率Dropout=0.4，相應的網絡結構如圖5所示。

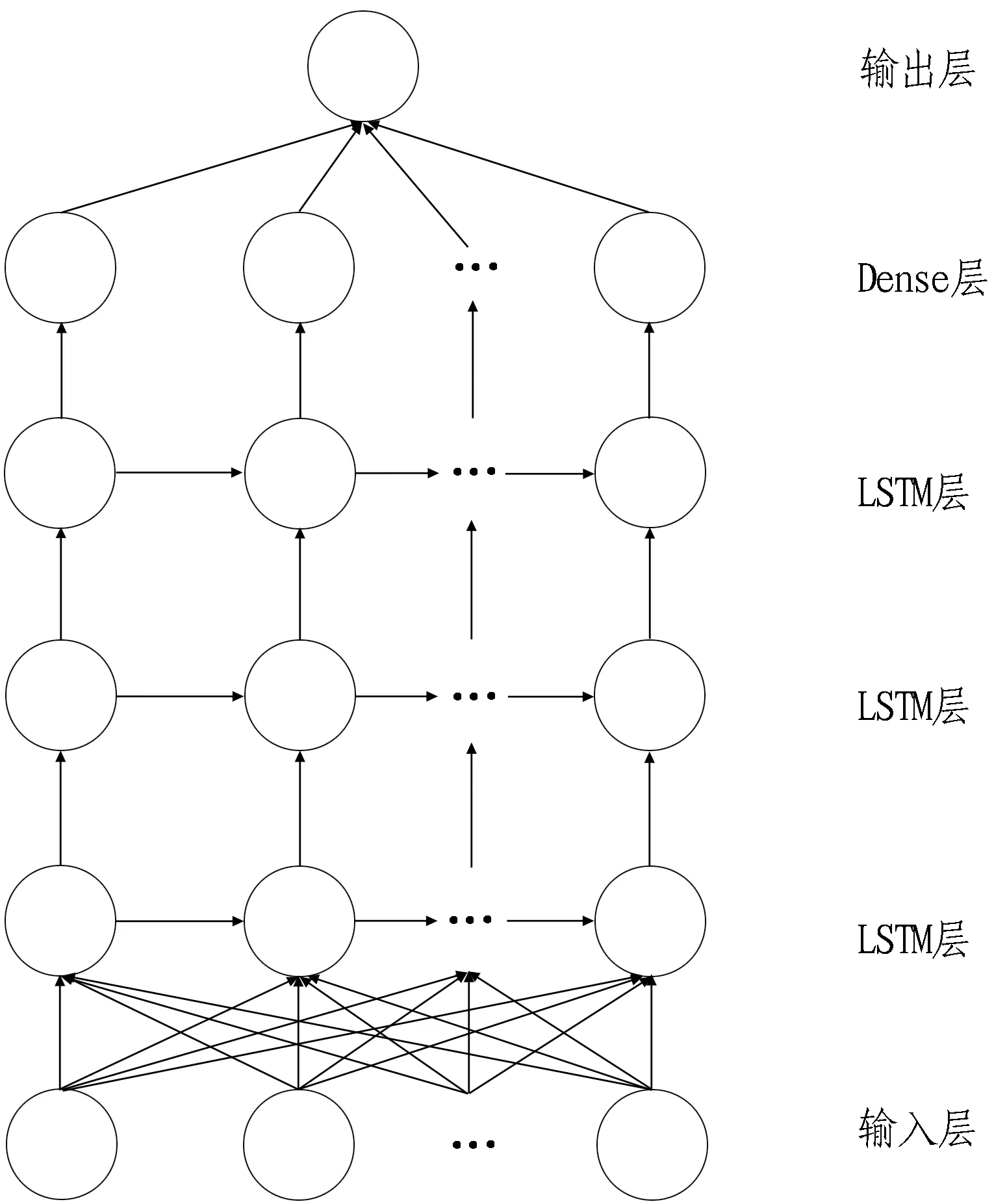
圖5 LSTM預測模型網絡結構Fig.5 Network structure of LSTM prediction model

在模型訓練過程中，將模型的迭代次數iter、學習率lr和模型隱含層單元數Uniti(i=1,2,3,4)確定為該模型的待尋優超參數，并基于試算法確定超參數的取值區間，基于交叉驗證網絡搜索的方式確定最優的超參數組合。LSTM預測模型超參數尋優結果如表2所示。

表2 LSTM預測模型超參數尋優結果Table 2 Hyperparameters optimization results of LSTM prediction model

根據確定的LSTM模型最優超參數組合(200,0.01,32,64,64,128)，基于440組訓練集數據進行模型構建，并進一步采用訓練集進行SVR模型構建，將核函數確定為表1中的高斯核函數。對于模型訓練過程中2個待優化超參數懲罰因子C和核函數參數G，分別基于試驗法確定其合適的取值范圍。懲罰因子C取值范圍為0.1～20.0，步長為0.5；核函數參數G取值范圍為0.01～2.00，步長為0.05。通過交叉驗證網格搜索的方式得到最優的參數組合為(10.1，1.01)。

根據確定的SVR模型最優超參數組合(10.1,1.01)，基于440組訓練集數據進行模型構建。

對于LSTM、SVR模型得到的訓練集預測結果，基于第2節設計的最優組合賦權方式(如式(5)所示)進行預測結果融合，進而得到LSTM-SVR模型在訓練集上的預測結果。經計算可知，相應的平均相對誤差MRE=8×10-4，小于0.001，能夠滿足模型設計的預測標準，說明該模型訓練完畢。

3.2.2 模型預測結果與分析

為驗證所構建的LSTM-SVR模型預測的準確性，基于測試集盾構豎向姿態數據進行模型性能測試。經計算可知，相應的平均相對誤差MRE=1.13%，小于2%；相關系數R2=0.935，大于90%。模型在測試集上的預測結果能夠滿足模型設計的要求，說明本文所構建的LSTM-SVR盾構豎向姿態預測模型能夠滿足實際工程需要。

為進一步討論本文所構建的預測模型的預測性能，將其與LSTM、SVR以及BP預測模型的預測結果進行對比，各模型在測試集上的預測結果如圖6所示。相應的預測結果指標計算如表3所示。從表3中可以看出，本文所構建的預測模型預測誤差最小，預測結果和實測數據的擬合效果最佳，進一步證實了所構建模型的預測精度和模型泛化能力。

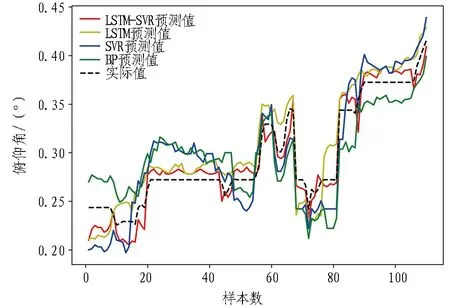
圖6 各模型測試集預測結果Fig.6 Predicted results of each model based on test set

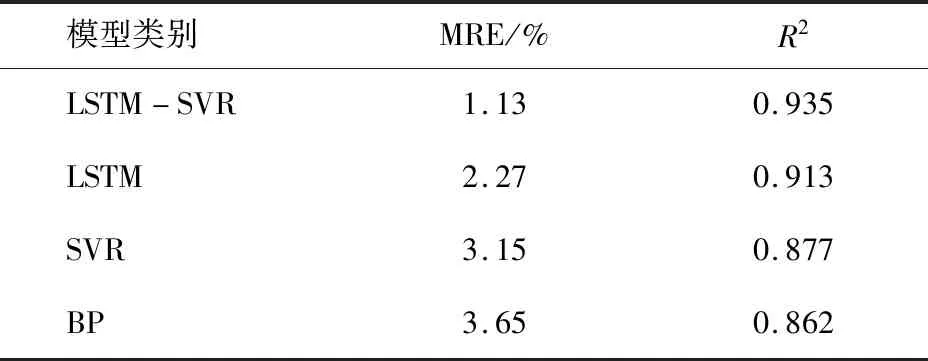
表3 各模型預測結果指標對比Table 3 Comparison of prediction results of each model

4 結論與討論

本文構建了基于LSTM-SVR的盾構豎向姿態組合預測模型,并依托實際盾構施工項目對其預測性能和適用性進行了驗證，得出如下結論。

1)基于LSTM-SVR的盾構豎向姿態組合預測模型在實際工程上的預測結果為MRE=1.13%，預測誤差較小；R2=0.935，模型預測結果和實測結果的擬合度較高，說明所提出的模型具有較好的預測性能，能夠滿足工程需要。

2)模型預測結果和單一預測模型LSTM、SVR以及BP模型的對比表明，本文所構建的基于LSTM-SVR的組合預測模型具有較高的預測精度。

3)本文僅針對盾構姿態中的豎向姿態進行了預測，尚未開展水平和轉動姿態的預測研究，后續建議進一步對其進行深入研究，已完善整個盾構姿態的預測體系，進而為盾構姿態控制提供輔助決策依據。