MARS-like Feistel 結構的量子攻擊

錢 新, 尤啟迪, 周 旋, 張 洋, 趙曉晶

1. 北京衛星信息工程研究所 信息科學工程技術中心, 北京 100086

2. 清華大學 計算機科學與技術系, 北京 100084

1 引言

Feistel 結構[1]自1973 年由Feistel 等人提出之后便成為了分組密碼設計的主流整體結構. Feistel 結構具備相似的加解密操作, 輪函數的選擇也較為靈活多變, 很多廣泛應用的分組密碼, 如DES、Camellia、FEAL、RC5 等都采用了Feistel 結構.

廣義Feistel 結構(generized Feistel structure, GFS) 是對Feistel 結構的一般形式的推廣, 可以隨著分支數的增加以更小規模的輪函數實現更大的分組, 從而在設計輕量級分組密碼時具備比Feistel 結構更大的優勢, 更適用于資源受限的通信環境中. 在1989 年美密會上, Zheng 等人[2]總結了三類廣義Feistel結構, 分別為Type-1 型、Type-2 型和Type-3 型廣義Feistel. 隨后Schneier 等人[3]將Feistel 結構推廣到了非平衡Feistel 結構, 此后出現了各種各樣的廣義Feistel 結構以及相應代表性的分組密碼, 包括CAST 256-like Feistel 結構(Type-1)[4], CLEFIA-like Feistel 結構(Type-2)[5], SMS4-like Feistel 結構[6], MARS-like Feistel 結構[7]. MARS-like Feistel 結構是在AES 候選密碼MARS 分組密碼的基礎上定義的一種廣義Feistel 結構. Moriai 等人[7]在2000 年給出了MARS-like 廣義Feistel 結構的隨機性證明, 并提出5 輪4 分支MARS-like Feistel 結構具有偽隨機性, 8 輪4 分支MARS-like 結構具有超偽隨機性; 當分支數為d時,d+1 輪MARS-like 結構具有偽隨機性, 2d輪MARS-like 結構具有超偽隨機性. 對于MARS-like 結構的密碼性質研究主要集中在不可能差分分析. 目前最好的結果是, 當分支數(子塊數)d為偶數時, 可以構造長為3d ?1 輪的不可能差分特征, 而當d為奇數時, 可以構造任意長輪數的不可能差分特征.

隨著量子理論的發展迅速, 量子信息科學的發展為密碼學的發展也帶來了一定挑戰. 后量子密碼成為了密碼學的研究熱點. 量子計算機的出現意味著人類計算能力的上限又得到極大的提升. Grover 提出了一種無序數據庫的標準搜索算法, 以Grover 算法[8]為代表的量子搜索算法以及推廣算法在量子計算環境下的計算復雜度是對經典算法的平方加速, 可用于加速密鑰的搜索, 對所有密碼產生了一定威脅; Shor算法[9,10]可用于分解大整數、求解離散對數, 在在量子計算環境下的計算復雜度是對經典算法的指數加速, 可用于相關公鑰密碼中的數學難題的加速求解, 對RSA、ECC 等為代表的公鑰密碼產生了一定威脅.相比于公鑰密碼, 由于對稱密碼算法通常不具有明顯的代數結構, 對稱密碼方案的設計也并非基于相應數學難題的計算困難性, 在一段時間內, 密碼學界的普遍觀點是, 針對對稱密碼沒有明顯有效的量子攻擊方法. 這種觀點在2010 年之后被Simon 算法[11]在量子區分攻擊Feistel 結構中的應用, 以及Simon 算法與Grover 算法的結合在量子密鑰恢復攻擊中的應用打破. Kuwakado 和Morii[12]首先利用Simon 算法構造了3 輪Feistel 結構的多項式時間量子區分器. 隨后, Even-Mansour 算法的量子密鑰恢復攻擊[13]、各種MAC 算法的偽造攻擊[14]、AEZ 的量子破解[15]、FX 結構的密鑰恢復攻擊[16], 以及Feistel 結構的量子密鑰恢復攻擊[17–21]和量子安全性證明[22]等相繼被提出. 廣義Feistel 結構的量子分析首先由Dong 等[23]提出并給出了Type-1、Type-2 廣義Feistel 結構的量子區分攻擊以及密鑰恢復. 隨后倪博煜等[24,25]和羅宜元[26]對相關結果進行了改進. 對SMS4-like 廣義Feistel 結構以及SMS4 算法的量子安全性分析由錢新等[27]提出.

需要指出的是, 考慮到針對對稱密碼進行量子分析時的攻擊者具備的不同攻擊能力, 可分為量子選擇明文攻擊和量子選擇密文攻擊[28]. 此外根據Zhandry[29]的研究工作, 分組密碼的量子分析模型主要有兩種: 標準安全模型、量子安全模型. 兩種分析模型的區別在于: 在標準安全模型中, 攻擊者對預言機的查詢只能通過經典方法進行, 對數據的處理可以使用量子計算機; 在量子安全模型中, 攻擊者對預言機的查詢可以以量子疊加態的方式進行, 并獲得相應的輸出疊加態, 對數據的處理也可以使用量子計算機.

本文基于量子安全模型, 結合Simon 算法和Grover 搜索算法, 給出了MARS-like 廣義Feistel 結構的量子選擇明文攻擊(quantum chosen-plaintext attack,QCPA)和量子選擇密文攻擊(quantum chosenciphertext attack, QCCA). 在量子選擇明文攻擊條件下, 給出d分支MARS-like 結構的d輪多項式時間量子區分攻擊, 以及2d輪量子密鑰恢復攻擊; 在量子選擇密文攻擊條件下, 給出d分支MARS-like 結構的d+1 輪多項式時間量子區分攻擊, 以及2d+1 輪量子密鑰恢復攻擊.

2 預備知識

2.1 Simon 算法

Simon 問題: 給定一個布爾函數f:{0,1}n →{0,1}n, 該布爾函數f滿足Simon 承諾, 即滿足x ⊕y={0n,s} ?f(x) =f(y). 求出n比特的s使得布爾函數f滿足Simon 承諾的問題即為Simon 問題. 在經典計算環境下, 利用生日攻擊解決這個問題的時間復雜度約為O(2n2). Simon 算法[11]由Simon 于1994 年提出, 主要用于解決Simon 問題——求解特殊布爾函數f的周期. 在量子計算環境下, 利用Simon 量子算法可以對布爾函數f以O(n) 的時間復雜度求出周期s.

Simon 算法包括以下步驟:

(1) 初始化: 將2n個量子比特的寄存器的狀態初始化為|0〉?n|0〉?n, 將Hadamard 變換應用于前n個量子比特得到平均疊加態

(2) 對量子預言機Uf:Uf|x〉|b〉=|x〉|b ⊕f(x)〉, 進行量子詢問得到當前的狀態

(3) 測量后n個量子比特, 前n個量子比特塌縮為狀態

(4) 將Hadamard 變換應用于前n個量子比特得到狀態

(5) 測量前n個量子比特, 顯然該疊加態中滿足y·s=1 則|y〉的振幅為0, 即

因此, 測量所有|y〉都必然滿足y·s=0.

重復以上步驟O(n) 次, 即可得到函數f的周期s.

Simon 算法對應的操作可以簡單描述為

Simon 算法的整個過程可以表示為

測量前n個量子比特, 所得|y〉滿足y·s= 0. 重復以上步驟O(n) 次, 可以得到n ?1 個線性無關方程組成方程組, 求解該線性方程組即可得到函數f的非零周期s.

需要指出的是, 參考Santoli 等人[18]提出在構建區分器進行密鑰恢復攻擊時, 無需真正計算得到函數f的周期s, 通過運行Simon 算法

得到滿足y·s=0 的, 對應n ?1 個線性無關方程組的向量|y1〉,|y2〉,|y3〉,···所張成的空間的維數. 如果函數f存在非零周期s, 也就意味著方程組y·s=0 存在非零解, 則向量|y1〉,|y2〉,|y3〉,···所張成的空間的維數至多為|s|?1; 如果函數f不存在任何周期, 也就意味著方程組y·s=0 不存在非零解, 則向量|y1〉,|y2〉,|y3〉,···所張成的空間的維數將可以達到|s|. 因此無需真正計算得到函數f的周期s, 即使函數f存在幾個局部周期, 或是周期不等于s的情況下, 仍可以通過檢查空間維數來驗證函數f的周期性.

2.2 Grove 算法

(1) 初始化: 將n量子比特的初始狀態設置為|0〉?n, 將Hadamard 變換應用于n量子比特得到相應的疊加態|φ〉

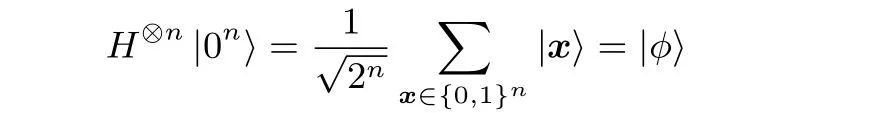
其中Grover 迭代包括以下幾個步驟:

(1) 翻轉目標態|x0〉的相位, 其余態保持不變

對目標態的相位反轉是通過查詢量子預言機Of來完成的;

(2) 進行n量子比特Hadamard 變換H?n;

(3) 保持|0〉態的相位不變, 翻轉其余態的相位

(4) 進行n量子比特Hadamard 變換H?n.

其中后面三步稱為擴散操作.

Grover 迭代對應的操作可以簡單描述為

2.3 量子密鑰恢復攻擊

Leander 等人于2017 年提出對FX 結構的量子密鑰恢復攻擊[16],該FX 結構滿足Enc(x)=Ek0(x+k1)+k2,通過構造函數f(k,x)=Enc(x)+Ek(x)=Ek0(x+k1)+k2+Ek(x),若猜測的密鑰正確,k=k0,滿足f(k,x)=f(k,x+k1). 若猜測的密鑰錯誤,k ?=k0, 不存在f(k,x)=f(k,x+k1),f(k,·) 不是周期的. Leander 等人在量子選擇明文條件下結合Simon 算法和Grover 算法來實施對FX 結構的量子攻擊.

本文分別在量子選擇明文條件和量子選擇密文條件下, 基于Simon 算法給出MARS-like 結構的具有多項式時間的量子區分器, 并基于Grover 算法結合Simon 算法對MARS-like 結構進行相應的量子密鑰恢復攻擊.

3 QCPA 條件下對MARS-like 結構的量子攻擊

MARS 密碼算法是AES 加密標準的五個最終候選算法之一, 其分組長度為128 比特, 包括四個分支, 采用非平衡Feistel 結構, 輪函數fi的輸出長度大于輸入長度. 其主要帶密鑰變換部分, 也稱密碼核(cryptographic core), 每輪中使用一個子塊作為輪函數的輸入, 得到三個32 比特的輸出, 分別和其他三個子塊相加或者異或, 因而每輪變換中作為輪函數輸入的一個子塊以及輪密鑰將影響到其他所有子塊. 在密碼核的前后分別是前向混合層和后向混合層. MARS-like 結構在MARS 密碼算法的密碼核的基礎上做了簡化, 其輪函數的輸出與其他分支之間均采用異或運算, 并且省略了作為輪函數輸入的子塊的移位變換,與MARS 密碼算法四個分支相比MARS-like 結構還可以有更多的分支.

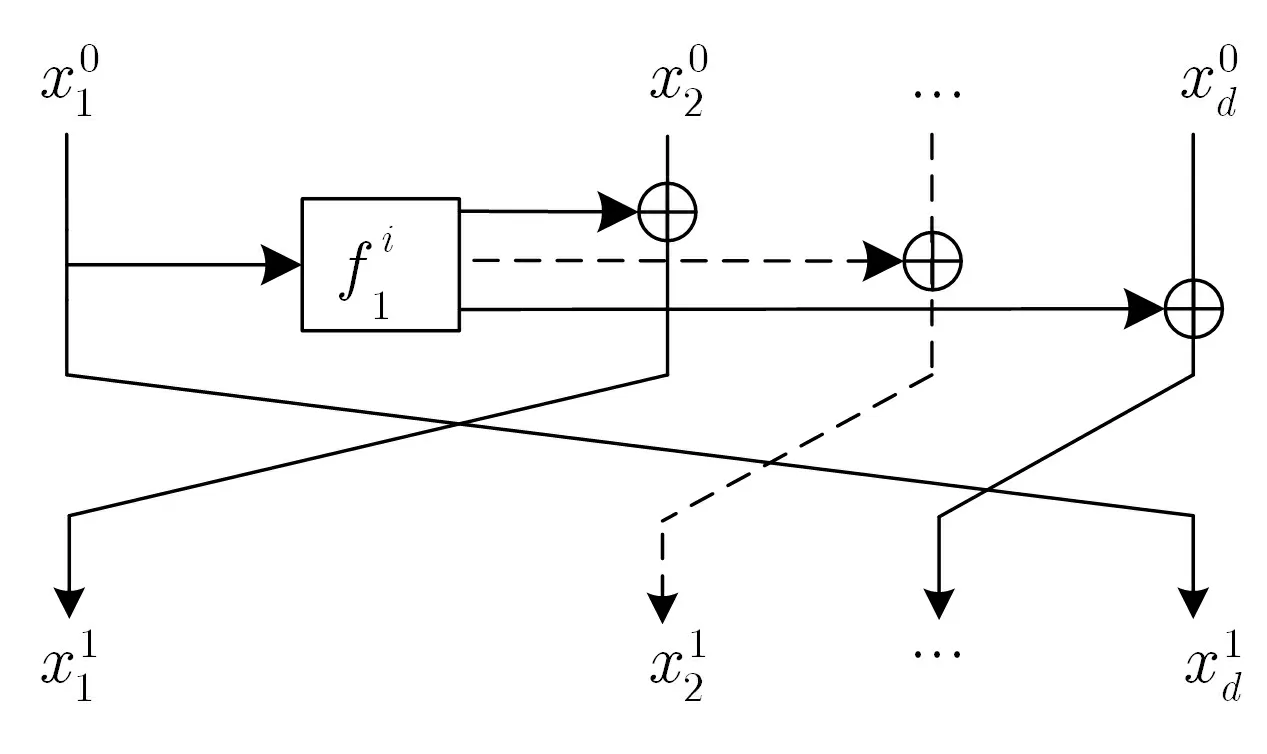
圖1 1 輪d 分支MARS-like 結構Figure 1 Structure of 1-round MARS-like of d branches

下面本文將先以四分支MARS-like 結構分別給出量子選擇明文條件和量子選擇密文條件下的具體量子攻擊過程, 并推廣到針對d分支MARS-like 結構的量子攻擊.

3.1 QCPA 條件下的量子區分攻擊

對四分支MARS-like 結構構造得到周期函數f如下:

下面驗證函數f為周期函數并求得其周期T.

當s=f3(f2(f1(x0)⊕x1)⊕f1(x0)⊕α0)⊕f3(f2(f1(x0)⊕x1)⊕f1(x0)⊕α1) 時, 顯然有f(0,x)=f(1,x ⊕s), 因此驗證得到函數f滿足Simon 承諾, 具有周期T=1||s.

借助周期函數f構造具有多項式時間的4 輪量子區分器如圖2 所示.

圖2 四分支MARS-like 結構的4 輪量子區分器Figure 2 4-round quantum distinguisher on MARS-like of 4 branches

推廣至一般情形, 對d分支MARS-like 結構構造得到周期函數f如下:

類似地可驗證函數f為周期函數并求得其周期T=1||s, 其中

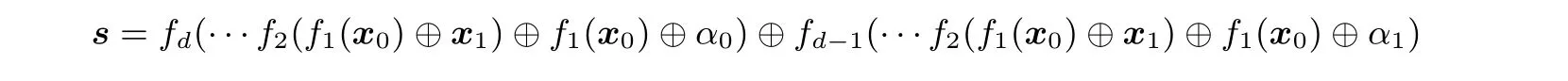
借助周期函數f構造可具有多項式時間的d輪量子區分器, 進行量子區分攻擊.

3.2 QCPA 條件下的量子密鑰恢復攻擊

8 輪量子密鑰恢復攻擊如圖3 所示.

圖3 四分支MARS-like 結構的8 輪量子密鑰恢復攻擊Figure 3 8-round quantum key recovery attack on MARS-like of 4 branches

利用量子區分器進行r輪量子密鑰恢復攻擊過程如下:

整體攻擊架構如圖4 所示.

圖4 整體攻擊架構Figure 4 Construction of quantum attack

4 QCCA 條件下對MARS-like 結構的量子攻擊

和QCPA 條件中不同的是, 在QCCA 條件下敵手不僅可以詢問量子加密預言機, 還可以訪問量子解密預言機.

4.1 QCCA 條件下的量子區分攻擊

對四分支MARS-like 結構構造得到周期函數f如下:

當s=α0⊕α1時, 有f(0,s)=f(1,x ⊕s), 驗證得到函數f滿足Simon 承諾, 具有周期T=1||s.借助周期函數f構造具有多項式時間的5 輪量子區分器如圖5 所示.

圖5 四分支MARS-like 結構的5 輪量子區分器Figure 5 5-round quantum distinguisher on MARS-like of 4 branches

推廣至一般情形, 對d分支MARS-like 結構構造得到周期函數f如下:

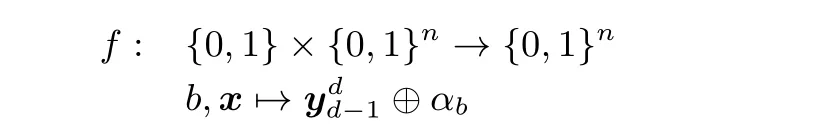
借助周期函數f構造可具有多項式時間的d+1 輪量子區分器, 進行量子區分攻擊.

4.2 QCCA 條件下的量子密鑰恢復攻擊

8 輪量子密鑰恢復攻擊如圖6 所示.

圖6 四分支MARS-like 結構的9 輪量子區分器Figure 6 9-round quantum key recovery attack on MARS-like of 4 branches

利用量子區分器進行r輪量子密鑰恢復攻擊過程如下:

圖7 整體攻擊架構Figure 7 Construction of quantum attack

5 總結

本文介紹了對MARS-like 結構在量子選擇明文條件下以及量子選擇密文條件下的量子攻擊, 總結了利用Simon 量子算法和Grover 搜索算法對分組密碼中的MARS-like 結構進行量子算法攻擊的方法. 本文給出了首次對MARS-like 結構的量子算法攻擊. 通過利用Simon 算法, 借助周期函數f構建量子區分器, 進行量子密鑰恢復攻擊. 在量子選擇明文條件下, 對四分支MARS-like 結構, 我們在4 輪量子區分器附加4 輪進行8 輪量子密鑰恢復攻擊; 對d分支MARS-like 結構, 我們在d輪量子區分器附加2d輪進行2d輪量子密鑰恢復攻擊. 在量子選擇密文條件下, 對四分支MARS-like 結構, 我們在5 輪量子區分器附加4 輪進行9 輪量子密鑰恢復攻擊; 對d分支MARS-like 結構, 我們在d+1 輪量子區分器附加d輪進行2d+1 輪量子密鑰恢復攻擊.