基于圖論方法的SHA-1 差分路徑的精準概率計算*

李婧瑜, 楊 陽,2, 曾 光, 李德剛

1. 中國人民解放軍戰略支援部隊信息工程大學 數學工程與先進計算國家重點實驗室, 鄭州 450001

2. 中國科學院 軟件研究所 可信計算與信息保障實驗室, 北京 100190

1 引言

SHA-1 算法由美國國家安全局[1]設計, 1994 年被美國國家標準與技術研究院(NIST) 發布作為聯邦信息處理標準(FIPS), 該算法一經提出就受到各國密碼學家的廣泛關注. 2005 年, 王小云教授[2]通過模差分攻擊技術和消息修改技術把對SHA-1 隨機碰撞攻擊的復雜度降到了269, 這也是首次將SHA-1 隨機碰撞攻擊的復雜度降到生日攻擊以下. 隨后, 很多團隊嘗試利用該方法對減輪的SHA-1 算法進行碰撞攻擊[3–6]. 直到2017 年, Stevens 與Google[7]宣布了一個成功的SHA-1 碰撞攻擊, 并且發布了兩份內容不同但SHA-1 散列值相同的PDF 文件作為證明. 這是目前為止對SHA-1 的最好的隨機碰撞攻擊結果.對SHA-1 的另一攻擊手段是選擇前綴碰撞攻擊, 這一類的攻擊最好結果由Leurent 和Peyrin[8]在2020年發布, 他們以263.4的復雜度完成了對SHA-1 的選擇前綴攻擊.

在對SHA-1 的隨機碰撞攻擊和選擇前綴攻擊過程中, 構造差分路徑和根據差分路徑尋找碰撞是兩種攻擊中共同的步驟. 在構造差分路徑方面, 現已由早期的手動構造方法[2]發展為自動化的差分路徑構造算法[9–11]. 差分路徑的成立概率很大程度上決定了尋找碰撞的成功率和復雜度, 所以對概率的高精度刻畫在攻擊過程中是十分重要的. 在早期的SHA-1 碰撞攻擊研究過程中, 往往以充分條件的個數來決定差分路徑成立概率[12,13], 設由差分路徑推導的充分條件的個數為k, 則認為該差分路徑成立的概率大約為1/2k. 2007 年, Mendel 等人[14]提出了在允許比特擴展且局部碰撞之間相互獨立的條件下, 對攻擊復雜度的評估方法. 2011 年, Manuel[15]證明了目前公布的擾動向量只有Type-I 和Type-II 兩類. 隨后,Stevens[11]提出了聯合概率的概念, 給出的概率模型是在同時滿足所有局部碰撞的條件下得到的, 對差分路徑的成立概率刻畫的精度更高.

本文對Stevens 提出的基于聯合概率的差分路徑概率模型進一步分析, 給出其中第三部分的所有結構和相應的概率特征, 最后給出實例以佐證.

2 SHA-1 算法

SHA-1 算法采用MD 迭代結構, 可以將任意長度的輸入消息壓縮成160 比特的Hash 值. 算法分成消息填充、消息擴展和壓縮函數三個部分.

消息填充在輸入消息的最后先填充一個1, 再填充若干個0, 使得填充后的消息長度l滿足l ≡448 mod 512, 再將原始消息的長度轉換成64 比特二進制的形式填充到消息末尾, 此時消息長度是512 的整數倍, 這就是消息填充過程.

消息擴展設填充后的消息長度為512K比特, 每個512 比特為一個消息塊, 分別記為M0,M1,···,MK?1. 消息擴展過程是將每個512 比特的消息塊擴展成80 個32 比特的消息字. 每個消息塊由16 個32 比特的消息字組成, 將第k+1 個消息塊Mk記為W0,k,W1,k,··· ,W15,k, 則對Mk的消息擴展準則如下式, 其中RL(W,b) 代表將32 比特向量W循環左移b比特:

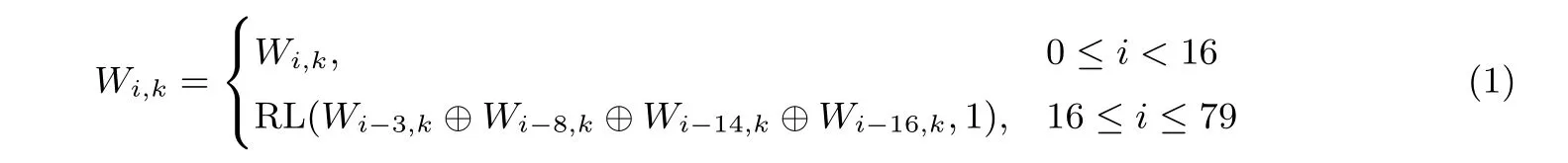
接下來擴展后的消息塊依次進入壓縮函數, 當處理第k+1 個消息塊Mk時, 壓縮函數以Mk和上一個消息塊的壓縮函數輸出IHVk=(ak,bk,ck,dk,ek) 作為輸入(ak,bk,ck,dk,ek為32 比特消息字), 輸出結果為160 比特的消息摘要IHVk+1, 即IHVk+1= Compress(IHVk,Mk), 處理第一個消息塊M0的初始值取值為IHV0=(a0,b0,c0,d0,e0):

這樣, 最后一個消息塊MK?1進入壓縮函數后的輸出結果IHVK即為最終的SHA-1 哈希值.

壓縮函數第k+1 個消息塊Mk經過消息擴展后進入壓縮函數的過程如下: 由上一步的壓縮結果IHVk= (ak,bk,ck,dk,ek), 令5 個寄存器的初始值為(Q0,Q?1,Q?2,Q?3,Q?4) = (ak,bk,RR(ck,30),RR(dk,30),RR(ek,30)), 其中RR(W,b) 代表將32 比特向量W循環右移b比特.

然后進行4 輪(每輪20 步) 迭代計算, 每次迭代均輸入一個擴展后的消息字, 第t(0≤t ≤79) 步的迭代方程為:Qt+1=RL(Qt,5)+Ft+RL(Qt?4,30)+Wt,k+ACt. 其中:

(1)Ft=ft(Qt?1,RL(Qt?2,30),RL(Qt?3,30)),ft是以三個比特為輸入的布爾函數, 其在每一輪的表達式分別為:

(2) ACt是輪常數, 其在每一輪的取值如下:

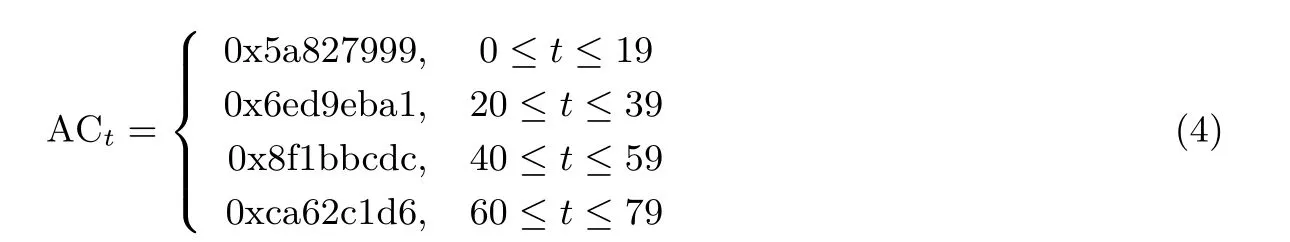
80 步迭代之后, 壓縮函數的輸出為IHVk+1= (ak+1,bk+1,ck+1,dk+1,ek+1) = (ak+Q80,bk+Q79,ck+RL(Q78,30),dk+RL(Q77,30),ek+RL(Q76,30)).

3 基于聯合概率的差分路徑概率模型

為了完整性, 本節介紹文獻[11] 所提出的一種新的基于聯合概率的差分路徑概率模型. 該模型通過提出概率實驗1, 從理論上對差分路徑的概率進行了精準刻畫. 進一步, 為了方便對實驗的成功率進行刻畫, 將實驗1 改進得到概率實驗2. 然而, 在概率實驗1 和2 中, 都存在取值空間過大、無法窮舉的問題.為了解決這一問題, 文獻[11] 結合圖論方面的知識, 通過對差分路徑上的寄存器差分和布爾函數差分的拆

概率實驗1

對于第一塊消息, 隨機選擇初始寄存器值 ?Qtb?4,··· ,?Qtb和第tb到te步的擴展消息字?Wtb,··· ,?Wte, 然后計算第一塊消息在第tb到te步的布爾函數值并更新寄存器值, 其中t=tb,··· ,te:

然后根據SHA-1 算法的壓縮函數計算每一步的布爾函數值, 并更新寄存器值, 其中t=tb,··· ,te:

得到兩塊消息相關變量的取值后, 判斷兩個消息塊的寄存器差分和布爾函數差分是否與差分路徑吻合, 即判斷:

對于第二塊消息, 各個變量的計算方法與實驗1 一致. 判斷實驗是否成功的條件也與實驗1 一致.

可以看到, 實驗1 在第一塊消息上首先隨機選擇消息字, 再計算寄存器值. 而實驗2 與這一過程相反,即先隨機選擇寄存器值, 再計算消息的值. 經過實驗1 到實驗2 的轉變, 隨機選擇的變量完成了由兩類向一類的整合(實驗1 需要隨機選擇寄存器值和消息值兩類變量, 而實驗2 中需要隨機選擇的變量只有寄存器值一類).

第一部分

設差分路徑上非零的寄存器差分對應的比特位集合為GΔQ={(j,i)|?Qj[i]?= 0, j ∈ {tb ?3,··· ,te}, i ∈{0,··· ,31}}. 對于集合GΔQ中元素(j,i), 為了取得實驗2 的成功, 若?Qj[i] = +1,則隨機選擇的第一塊消息的 ?Qj必須滿足 ?Qj[i] = 0; 若?Qj[i] =?1, 則隨機選擇的第一塊消息的 ?Qj必須滿足 ?Qj[i] = 1, 這兩種情況的成立概率均為1/2. 所以GΔQ中的比特位滿足差分路徑的概率為pΔQ=2?|GΔQ|.

第二部分

給定差分路徑上第t步的布爾函數的三個輸入寄存器差分為?Qt?1,?Qt?2,?Qt?3, 對于滿足這三個寄存器差分的3 對寄存器取值, 將第b比特上所有可能的布爾函數輸出差分組成的集合記為Vt,b:

設SF={(t,b)||Vt,b|> 1}, 考慮滿足以下兩個條件的寄存器比特位(j,i): 1○對應的寄存器差分為零, 即?Qj[i]=0; 2○(j+1,i),(j+2,i ?2),(j+3,i ?2) 中至少有一個在集合SF中. 即

第三部分

命題2在上述分割方法下, 差分路徑的概率分解成若干個因子的乘積:

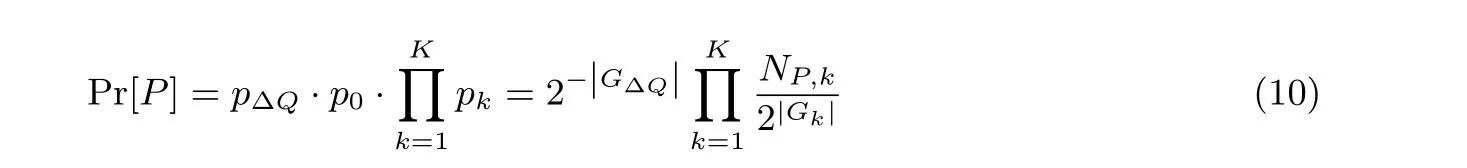
4 基于圖論方法的精確概率特征計算

本小節對第3 節中的第三部分概率做進一步的理論分析. 按照第3 節的分割方法, 第三部分主要考慮布爾函數輸出差分不唯一時的成立概率. 對于SHA-1 算法在后三輪所采用的布爾函數—異或函數和擇多函數, 分析總結其輸出差分規律. 進一步, 結合圖論相關知識分析第三部分中連通分支的結構特征和概率特征. 首先提出本文所涉及的圖論的基本概念.

定義1一個集合的元素和它們之間的某種關系稱為圖. 具體地說, 圖是一個二元組(V,E), 其中集合V稱為節點集, 集合V中由兩個元素組成的無序對的集合E稱為邊集. 圖的節點集中的元素稱為節點,邊集中的元素稱為邊. 節點的數目|V| 稱為圖的階, 邊的數目|E| 稱為圖的邊數.

例 1給定G= (V,E), 其中節點集V={v1,v2,v3,v4,v5}, 邊集E={(v1,v2),(v3,v4),(v1,v5),(v5,v5)}. 這便定義出一個圖. 節點v1和v2稱為邊(v1,v2) 的端點, 反過來也稱邊(v1,v2)連接節點v1和v2.

定義2(點和點的相鄰) 如果圖上兩點被同一條邊相連, 則稱該兩點在圖中相鄰.

定義3(點和邊的關聯) 如果在圖G中節點v是邊e的一個端點, 則稱節點v與邊e在圖G中相關聯.

定義4(節點的度) 圖G中節點v所關聯的邊的數目稱為節點v的度, 記為dG(v) 或d(v).

定義5圖G中一個點邊接續交替出現的序列w=vi0ei1vi1ei2···eikvik稱為圖G的一條途徑, 其中vi0,vik分別稱為途徑w的起點和終點,w上其余節點稱為中途點. 圖G中邊不重復出現的途徑稱為跡. 圖G中頂點不重復出現的跡稱為路.

定義6設G是一個圖,V′?V(G). 以V′為節點集, 以G中兩端點均屬于V′的所有邊作為邊集所組成的子圖, 稱為G的由節點集V′導出的子圖, 簡稱為G的點導出子圖, 記為G|V′|.

定義7(圖中兩點的連通) 如果在圖G中u,v兩點間有路相通, 則稱節點u,v在圖G中連通. 若圖G中任兩節點都相通, 則稱圖G是連通圖.

定義8(圖的連通分支) 若圖G的節點集V(G) 可劃分為若干非空子集V1,V2,···Vw, 使得兩節點屬于同一子集當且僅當它們在G中連通, 則每個點導出子圖G|Vi| 為圖G的一個連通分支(i=1,2,··· ,w).G的連通分支的個數稱為G的連通分支數.

在本文所涉及的圖中, 節點分為兩類, 一類代表寄存器比特位, 另一類代表布爾函數比特位. 另外, 圖中相鄰的兩個點屬于不同類節點, 即邊的端點均為一個寄存器比特位和一個布爾函數比特位.

定理1對于異或函數f(X,Y,Z)=X ⊕Y ⊕Z, 給定X,Y,Z上的差分?X,?Y,?Z, 定義集合

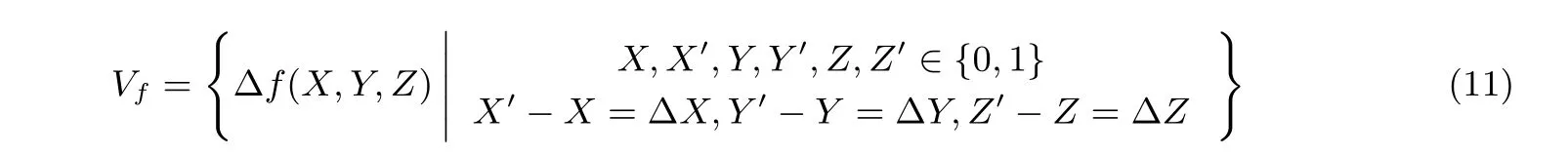
則|Vf|> 1??X,?Y,?Z中有且僅有一個為非零, 即存在六種輸入寄存器差分的取值使得布爾函數的輸出差分不唯一, 這六種取值分別為三個輸入中的其中一個為正差分或負差分.

證明:1)|Vf|>1??X,?Y,?Z中有且僅有一個為非零.

在布爾函數f(X,Y,Z) =X ⊕Y ⊕Z的三個輸入比特上, 每個比特上的差分都有三種取值: 0、+1和?1, 所以三個輸入比特差分共有27 種取值情況. 將?X,?Y,?Z的27 種取值遍歷, 計算每種取值下的集合Vf, 將所有|Vf|> 1 的情況匯總得到表1(左), 可以從中發現寄存器差分的規律: 輸入寄存器差分?X,?Y,?Z中有且僅有一個為非零.

2) ?X,?Y,?Z中有且僅有一個為非零?|Vf|>1.

當?X,?Y,?Z中有且僅有一個為非零時, 由表1(左),|Vf|>1.

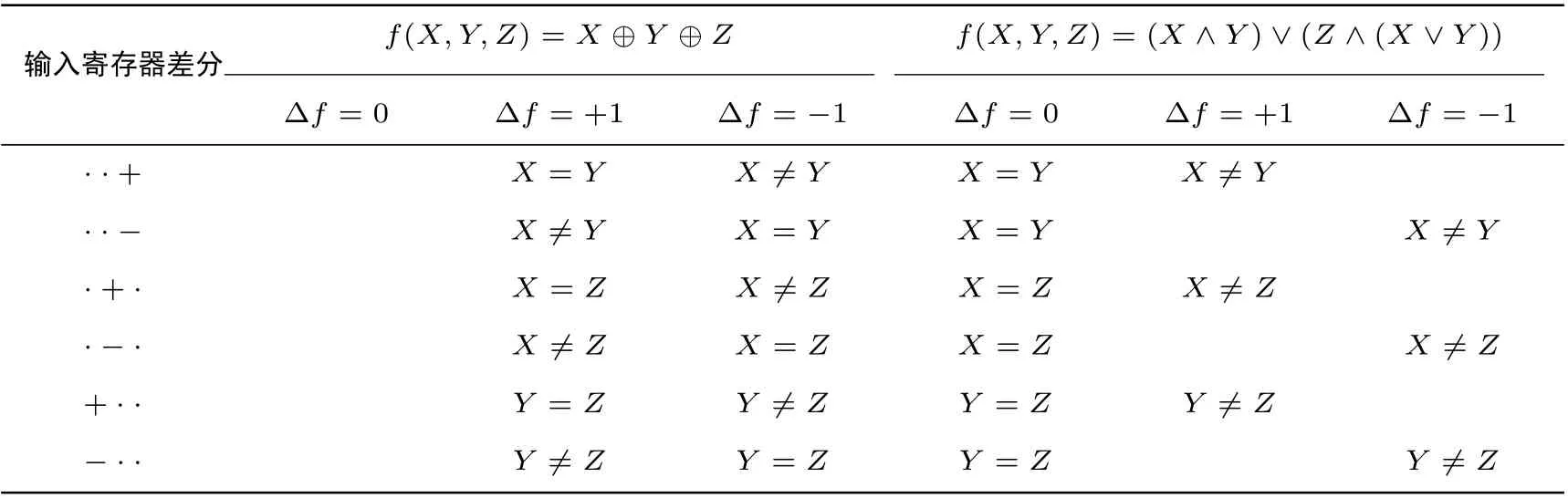
表1 布爾函數輸出差分不唯一的所有情況Table 1 All cases where Boolean function output difference is not unique

表注: 每個Vf中的元素下的等式或不等式是為了得到相應的輸出差分而對兩個不存在差分的寄存器的取值提出的制約條件. 以第一行為例, 當三個輸入寄存器比特上的差分為··+ 時(即?X=0、?Y=0和?Z=+1),集合Vf中存在兩個元素: +1 和?1. 其中,?f(X,Y,Z)=+1 時要求X′=X=Y=Y′,而?f(X,Y,Z)=?1 時要求X′=X,Y=Y′,X ?=Y.

定理2將定理1 中的異或函數替換成擇多函數f(X,Y,Z)= (X ∧Y)∨(Z ∧(X ∨Y)), 結論依然成立.

證明:將異或函數替換成擇多函數f(X,Y,Z) = (X ∧Y)∨(Z ∧(X ∨Y)), 同樣計算27 種輸入差分取值下的集合Vf, 將|Vf|>1 的情況匯總得到表1(右). 其余證明過程與定理1 同理.

根據定理1 和定理2 可以得到以下定理和推論:

定理3連通分支FQk中每個布爾函數比特位的度均為2.

證明:在連通分支FQk(k=1,2,··· ,K) 中, 對于(t,b)∈SF, 由定理1 和定理2 可知,Ft[b] 的三個輸入寄存器差分?Qt?1[b], RL(?Qt?2,30)[b], RL(?Qt?3,30)[b] 中有且僅有一個為非零, 其中20≤t<79,b=0,1,··· ,31. 即在連通分支FQk(k=1,2,··· ,K) 中, 每個布爾函數比特位(t,b)∈SF一定與兩個輸入寄存器比特位相連接, 故而該點在連通分支中的度為2.

定義9將含有l個布爾函數比特位、l+1 個寄存器比特位的連通分支稱為l-l+1 型連通分支.

綜合以上分析, 所有連通分支的類型為1-2 型、2-3 型、3-4 型等. 顯然, 1-2 型和2-3 型連通分支只有一種結構, 而3-4 型連通分支由于一個寄存器比特位的度的不確定性可以分為兩種結構, 圖1 列舉了1-2型、2-3 型、3-4 型連通分支的所有結構. 在每個類型的連通分支中, 上層節點均為布爾函數比特位, 自左向右分別記為F1,F2,··· ,下層節點均為寄存器比特位, 自左向右分別記為Q1,Q2,··· .

定理4在由Type-I 和Type-II 類擾動向量得到的差分路徑中, 圖1 中3-4 型(2) 的結構不存在.

圖1 連通分支的結構Figure 1 Structure of connected branches

證明:首先分析一個寄存器比特位在連通分支中的結構特點. 對于寄存器比特Qj[i], 其中i=0,1,··· ,31 且20≤j<79, 存在三個布爾函數比特位以其作為輸入, 分別為

由集合SQ的含義以及定理3, 當?Qj[i] = 0 且三對寄存器比特Qj?1[i+2 mod 32] 和Qj?2[i+2 mod 32]、Qj+1[i ?2 mod 32] 和Qj?1[i]、Qj+2[i ?2 mod 32] 和Qj+1[i] 中至少有一對比特上的差分為零和非零的組合時, 有(j,i)∈SQ.

下面證明連通分支中一個寄存器比特位的度不可能為3.

假設(j,i)∈SQ且在連通分支中的度為3, 則(j,i)∈SQ與三個布爾函數位(分別為(j+1,i),(j+2,i ?2),(j+3,i ?2)∈SF) 相連接, 則三對寄存器比特Qj?1[i+2 mod 32] 和Qj?2[i+2 mod 32]、Qj+1[i ?2 mod 32] 和Qj?1[i]、Qj+2[i ?2 mod 32] 和Qj+1[i] 上的差分均為零和非零的組合, 具體有8種情況見表2.

表2 d((j,i))=3 時要求寄存器差分的取值情況Table 2 Value of register differential required for d((j,i))=3

針對表2 中的第一種情況進行分析: 首先, 在后60 步差分路徑上, 寄存器上的差分(不考慮差分的正負) 與擾動向量是一致的, 即?Qj[i]?= 0 當且僅當擾動向量滿足DVj?1[i] = 1, 反之, ?Qj[i] = 0 當且僅當擾動向量滿足DVj?1[i] = 0. 所以, 表2 的第一種情況要求擾動向量滿足: 對于i= 0,1,··· ,31 和20≤j< 79, DVj?1[i],DVj?2[i+2 mod 32],DVj[i ?2 mod 32],DVj+1[i ?2 mod 32] 的取值為0, 而DVj?3[i+2 mod 32],DVj?2[i],DVj[i] 的取值為1. 文獻[15] 中證明了最優擾動向量存在兩類(Type-I和Type-II), 目前為止對SHA-1 的碰撞攻擊中用到的擾動向量有

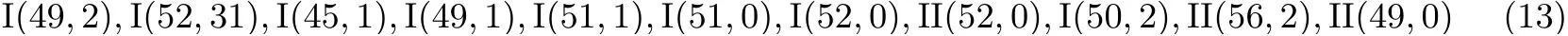
附錄列出了這些擾動向量的后60 步在通式I(K,0) 和II(K,0) 中涉及的最大范圍. 將上述條件和附錄對比發現Type-I 和Type-II 類擾動向量不能滿足表2 中第一種情況. 對表2 中另外7 種情況進行同理分析, 最終結論為: 對于Type-I 和Type-II 類擾動向量, 表2 中的8 種情況均不可能存在, 故連通分支中寄存器比特位的度小于3, 即圖1 中3-4 型(2) 的結構不存在.

定理5在由Type-I 和Type-II 類擾動向量得到的差分路徑中, 圖1 中3-4 型(1) 的結構不存在.

證明:對于圖1 中3-4 型(1) 的結構, 固定Q2點為(j,i), 在此基礎上分析其他寄存器比特位和布爾函數位的取值情況. 與Q2點相連的兩個布爾函數位F1和F2從(j+1,i),(j+2,i ?2),(j+3,i ?2) 中選擇, 由于F1和F2兩點在3-4 型(1) 結構中的地位是不對等的, 所以共有6 種選擇. 然后, 在F2的除Q2外的兩個輸入寄存器比特中選擇一個確定為Q3點(2 種選擇), 再在以Q3點為輸入的除F2外的兩個布爾函數位中選擇一個確定為F3(2 種選擇). 最后確定Q1和Q4(均有2 種選擇). 所以, 在固定節點Q2點后, 3-4 型(1) 結構的連通分支上所有點的取值共有6×2×2×2×2=96 種情況.

與定理4 的證明過程同理, 將96 種情況對照附錄進行分析, 發現Type-I 和Type-II 類擾動向量不能滿足上述條件. 另外發現有些情況本身就存在矛盾. 總之, 96 種情況均不可能存在, 所以3-4 型(1) 結構的連通分支在由Type-I 和Type-II 類擾動向量得到的差分路徑中不可能存在.

推論2在由Type-I 和Type-II 類擾動向量得到的差分路徑中, 本文的概率模型的第三部分中連通分支的結構只可能有1-2 和2-3 型兩種.

證明:假設存在l-l+1 型連通分支(l> 3), 則一定內嵌有3-4 型(1) 和3-4 型(2) 結構. 結合定理4 和定理5, 在由Type-I 和Type-II 類擾動向量得到的差分路徑中, 只可能有1-2 和2-3 型兩種結構的連通分支.

定理6l-l+1 型連通分支SQ中寄存器比特位的取值滿足差分路徑的概率為2/2l+1.

證明:設一個l-l+1 型連通分支SQ中的寄存器比特位分別為(j1,i1),··· ,(jl,il),(jl+1,il+1), 對應Qj1[i1],··· ,Qjl[il],Qjl+1[il+1]. 其中一個位置Qjm[im],m=1,2,··· ,l在取定0 或1 其中一個值后,由表1 可以確定這些比特位的取值以得到差分路徑指定的布爾函數輸出差分, 即與Qjm[im] 的關系都確定為“相等” 或“不相等”. 也就是說, 當確定Qj1[i1],··· ,Qjl[il],Qjl+1[il+1] 中的其中一個取值后, 其余比特位的取值也隨之確定. 所以Qj1[i1],··· ,Qjl[il],Qjl+1[il+1] 一共在兩種取值下可以滿足差分路徑. 而l+1 個比特位的取值空間中存在2l+1個元素, 所以這些比特位滿足差分路徑的概率為2/2l+1.

5 實例及評估

本節以三段具體的差分路徑為例, 對其分別按照實驗的方法、計數充分條件的方法和本文第3、4 節的方法進行概率計算, 綜合三個結果對本文的概率模型進行評估.

實例1

2005 年,王小云[2]針對SHA-1 算法提出了模差分攻擊的方法,以269的復雜度給出了對全輪SHA-1算法的碰撞攻擊. 隨后文獻[16] 對其用到的差分路徑進行了全輪分析, 本文以文獻[16] 整理的差分路徑進行概率分析. 以文獻[16] 中Figure 3 的第46–56 步的差分路徑(記為P46–56) 為例進行概率分析, 差分路徑及對應的充分條件如表3, 表中的數字代表存在擾動(第2 列) 或差分不為零(第3–7 列) 的比特位,“-” 代表32 位無擾動或全零差分.

表3 第46–56 步上的差分路徑Table 3 Differential path over Steps 46–56

命題3當按照充分條件的個數計算差分路徑的概率時, Pr[P46–56]=1/219.

證明:由于在第46–56 步上的充分條件的個數為19, 根據每個充分條件成立的概率為1/2 的原則,所以差分路徑P46–56的概率為1/219.

命題4當按照本文的差分路徑概率模型計算概率時, Pr[P46–56]=1/216.

證明:當按照第3 節和第4 節中的差分路徑概率模型, 差分路徑上寄存器差分的情況為:

(1)δRL(Q42,30)=0;

(2) ?Q43,?Q44,?Q46,?Q48,?Q50上無差分, ?Q45,?Q47,?Q49,?Q51均在第1 位上存在正差分;

(3)δQ57=0.

進而可以確定集合GΔQ為GΔQ={(45,1),(47,1),(49,1),(51,1)}, 共四個元素, 所以這一部分對應的概率為1/24.

然后確定集合SF的所有元素. 對于(t,b)∈SF, ?Qt?1[b],RL(?Qt?2,30)[b],RL(?Qt?3,30)[b] 中至少有一個輸入差分為非零. 故將每個非零寄存器差分作為布爾函數的輸入, 他們影響的所有布爾函數差分如表4, 其中“無” 代表布爾函數輸出的32 個比特上差分均為0.

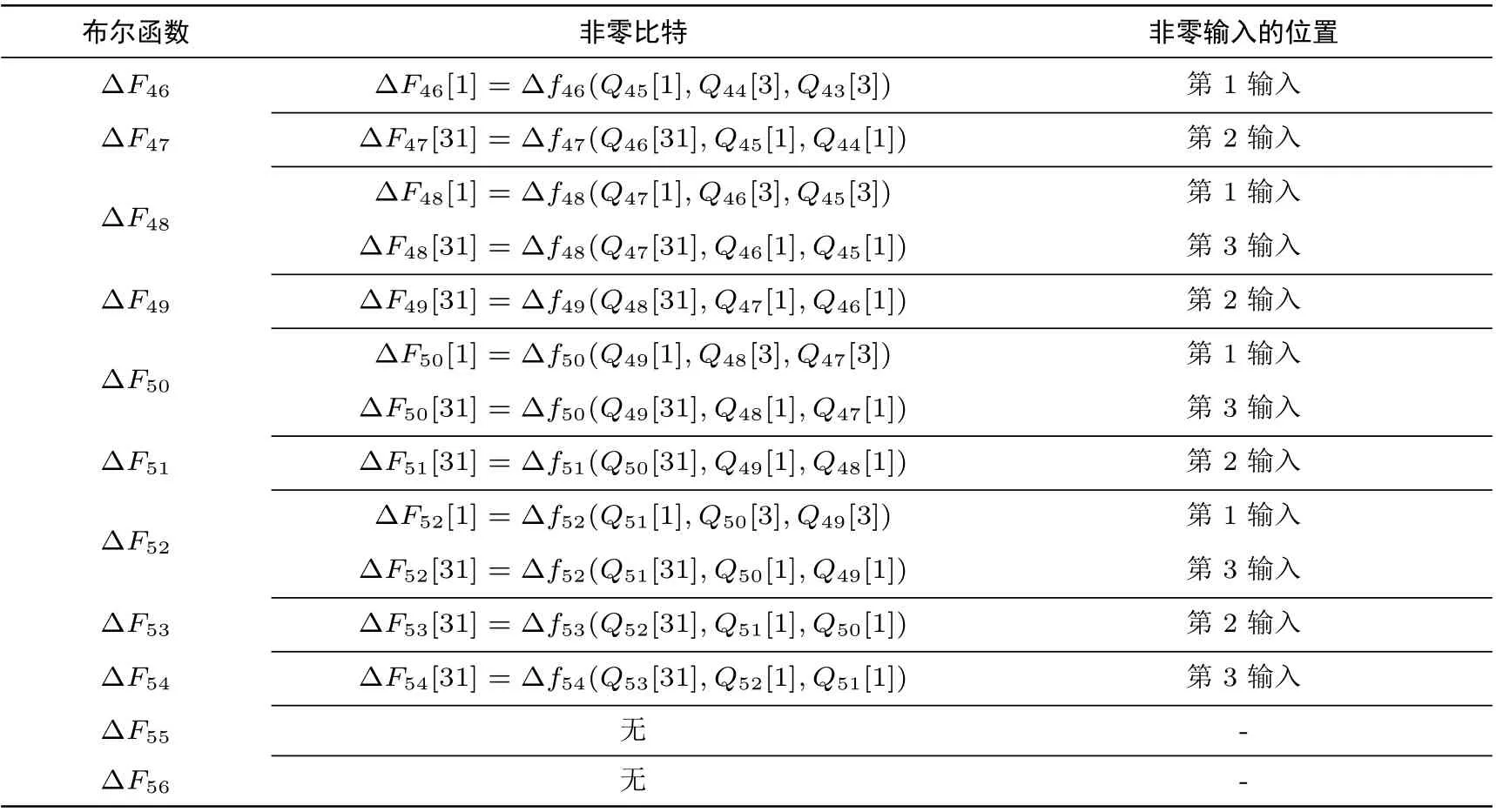
表4 差分路徑P46–56 上非零布爾函數差分與非零輸入的關系Table 4 Nonzero Boolean function differences and nonzero inputs on differential path P46–56

這 12 個布爾函數比特位均滿足有且只有一個輸入差分非零, 根據定理1 確定集合SF={(46,1),(47,31),(48,1),(48,31),(49,31),(50,1),(50,31),(51,31),(52,1),(52,31),(53,31),(54,31)}. 進而集合SQ={(44,3),(43,3),(46,31),(44,1),(46,3),(45,3),(47,31),(46,1),(48,31),(48,3),(47,3),(49,31),(48,1),(50,31),(50,3),(49,3),(51,31),(50,1),(52,31),(52,1),(53,31)}.SF和SQ形成集合FQ, 對于(j,i)∈SQ和(t,b)∈SF, 若Qj[i] 是Ft[b] 的一個輸入, 則在FQ 中將(j,i) 和(t,b) 連接起來.所連成的圖如圖2 所示(圖2與圖1的節點排列方式相同, 連通分支的布爾函數節點位于上層, 寄存器節點位于下層).

圖2 第46–56 步差分路徑的所有連通分支Figure 2 All connected branches of differential path over Steps 46–56

可以看到, FQ 中的元素一共形成9 個連通分支, 其中有6 個1-2 型連通分支和3 個2-3 型連通分支.依據定理4, 1-2 型連通分支的概率為2/22, 2-3 型連通分支的概率為2/23. 綜上, 這段第46–56 步的差分路徑成立概率為2?4×(2/23)3×(2/22)6=1/216.

實例2

本文還對文獻[16] 中Figure 3 中的第66–79 步的差分路徑進行了相同過程的概率分析, 按照充分條件的個數計算得到的差分路徑的概率為1/230, 而按照第3 節和第4 節中的差分路徑概率模型計算得到的概率為1/221, 其中第三部分的連通分支結構都是1-2 型的, 具體計算過程不再贅述.

實例3

命題5當按照充分條件的個數計算差分路徑的概率時, Pr[P8–16]=1/233.

證明:由于在第8–16 步上的充分條件的個數為33, 根據每個充分條件成立的概率為1/2 的原則, 所以差分路徑P8–16的概率為1/233.

命題6當按照充分條件的個數計算差分路徑的概率時, Pr[P8–16]=1/228.

證明:當按照第3 節和第4 節中的差分路徑概率模型, 差分路徑上寄存器差分的情況為:

(1)δRL(Q4,30)=24+25+26+27+28?29?228+231;

(2) ?Q5–?Q16上的差分如表5;

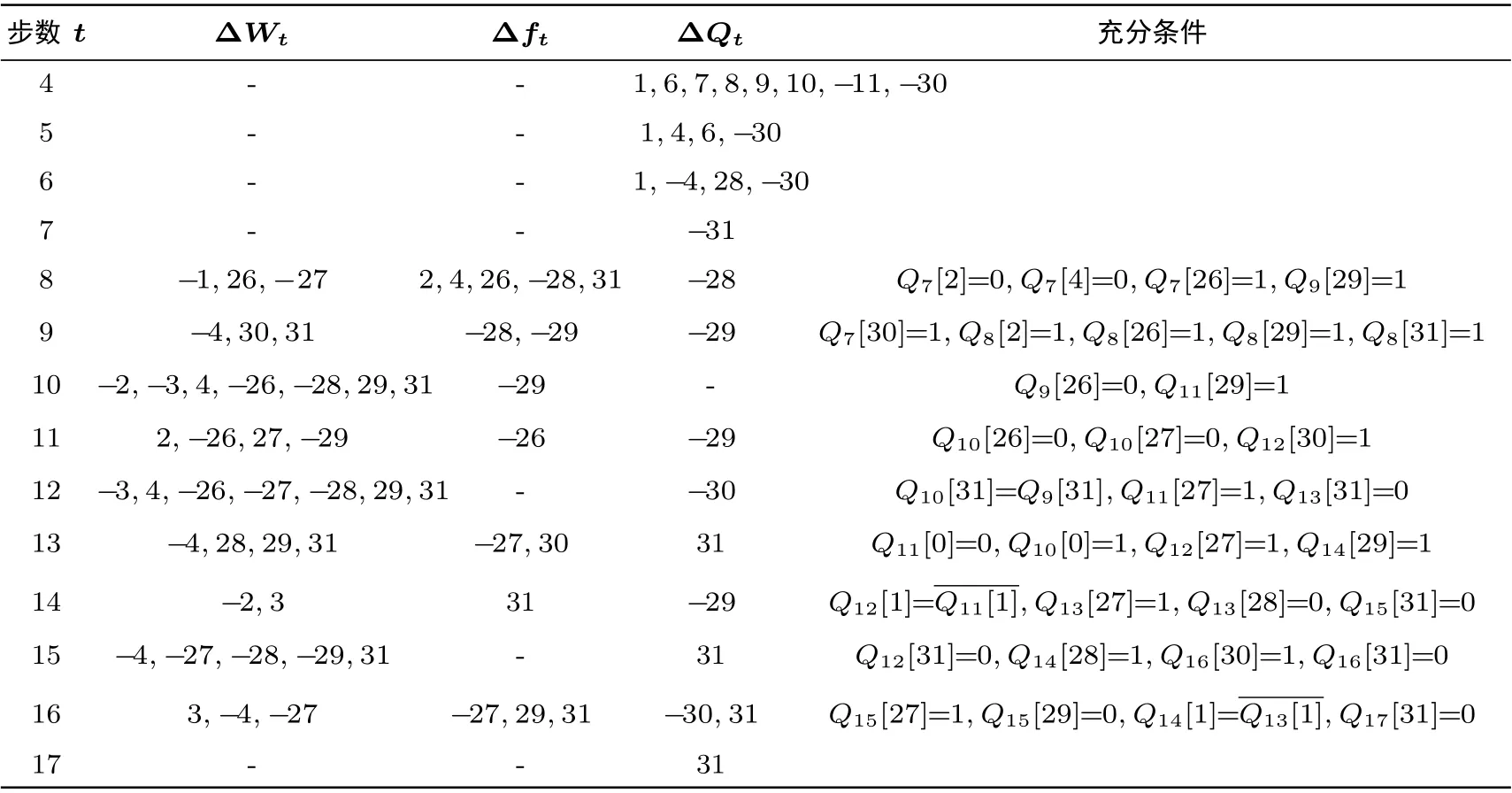
表5 第8–16 步上的差分路徑P8–16Table 5 Differential path over Steps 8–16

(3)δQ17=231.

進而可以確定集合GΔQ為?Q5–?Q16上所有差分為非零的比特位, 根據表5 可知GΔQ中共有18個元素, 所以這一部分對應的概率為1/218.

然后確定集合SF的所有元素. 對于(t,b)∈SF, ?Qt?1[b], RL(?Qt?2,30)[b], RL(?Qt?3,30)[b] 中至少有一個輸入差分為非零. 將由表5 中布爾函數上的非零差分總結在表6 中, 分析非零寄存器差分的輸入情況.

表6 差分路徑P8–16 上非零布爾函數差分與非零輸入的關系Table 6 Nonzero Boolean function differences and nonzero inputs on differential path P8–16

由定理1 可知, 當存在兩個及以上的輸入存在非零差分時, 布爾函數的輸出值唯一. 所以可以確定集合SF為:

進而集合SQ為:

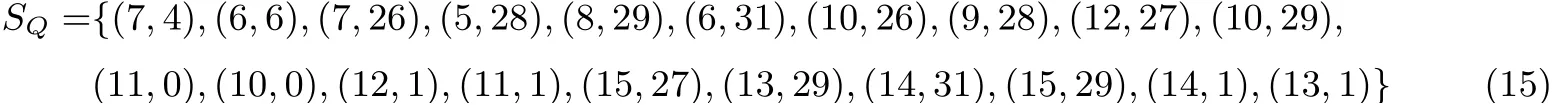
SF和SQ形成集合FQ, 對于(j,i)∈SQ和(t,b)∈SF, 若Qj[i] 是Ft[b] 的一個輸入, 則在FQ 中將(j,i) 和(t,b) 連接起來. 所連成的圖如圖3 所示(圖結構和節點的含義同圖2):

圖3 第6–18 步差分路徑的所有連通分支Figure 3 All connected branches of differential path over Steps 6–18

可以看到, FQ 中的元素一共形成10 個1-2 型連通分支. 依據定理6, 每個1-2 型連通分支的概率為2/22, 所以第8–16 步的差分路徑成立概率為2?18×(2/22)10=1/228.

本節的差分路徑實例從涵蓋的輪數上看, 既包含了第一輪的非線性路徑, 也包含了后三輪的線性差分路徑部分, 實驗結果可見本文的概率模型在刻畫差分路徑成立概率上的優越性. 從表7 的結果中可以發現,相較本文的概率模型, 按照充分條件的個數計算得到的差分路徑概率偏小. 這是因為本文的概率模型是針對差分路徑的整體進行概率分析的, 而充分條件個數的方法將差分路徑中的局部碰撞視為相互獨立的. 由于各個局部碰撞成立的充分條件可能會同一寄存器比特或消息比特做出約束, 充分條件之間存在內在的聯系, 所以按照每個充分條件的成立概率均為1/2、同時所有充分條件獨立的計算方法會使計算結果偏小.

表7 差分路徑實例的不同概率分析結果對比Table 7 Comparison of different probability analysis results of differential paths instance

6 總結

在對SHA-1 的碰撞攻擊過程中, 差分路徑的構造是非常重要的步驟, 將會直接影響后續尋找碰撞消息對的復雜度. 差分路徑的成立概率是考察其優劣的一個重要衡量指標, 所以更精確地刻畫差分路徑成立的概率有助于對差分路徑進行準確評估, 進而對整個碰撞攻擊的復雜度進行精準評估. 隨機碰撞分為差分路徑構造和消息搜索兩個階段, 利用本文的概率模型對文獻[16] 中后三輪的差分路徑進行分析, 得到其成立概率為1/292, 而該段差分路徑成立的充分條件個數為113 個, 這說明本文方法更貼近實際概率. 需要說明的是基于該路徑, 消息搜索階段可利用消息遞歸技術和高級消息修改技術進一步降低復雜度, 致使差分路徑概率與真實的碰撞攻擊復雜度存在差距. 本文對Stevens 提出的基于聯合概率的差分路徑概率模型進行分析, 得出了其中第三部分連通分支的結構特征和概率特征. 從理論上證明了對于兩類最優擾動向量, 不存在包含3 個及以上布爾函數比特的連通分支, 明確了每一類連通分支對應的成立概率. 完善之后的概率模型使得差分路徑的概率計算過程更為簡單, 且較之前的計算方法誤差更小.