考慮高速公路橫向坡道轉向行駛操縱穩定性的汽車軸距和輪距分析

謝欣然 李松玨 吳明虎 馮清 楊弘毅 魏登 楊鑫

摘要：為分析汽車軸距和輪距設計對操縱穩定性的影響，建立高速公路橫向坡道轉向行駛的汽車轉向動力學模型，并在MATLAB/Simulink軟件中建立相應的仿真模型。采用某型汽車設計軸距和輪距進行仿真，得到以不同速度在不同橫向坡度道路上轉向行駛時的橫擺角速度、側向加速度和質心側偏角。根據該型汽車的轉向特性和側翻閾值評價其在高速公路橫向坡道轉向行駛時的操縱穩定性，結果表明該型汽車的設計軸距和輪距滿足操縱穩定性要求。計算方法和仿真結果對整車設計具有指導意義。

關鍵詞：

整車設計; 橫向坡度; 轉向; 橫擺; 側偏; 操縱穩定性

中圖分類號：U462.33; TP391.92

文獻標志碼：B

Vehicle wheel-base and wheel-track analysis considering

handling stability of steering on transverse slope highway

XIE Xinran， LI Songjue， WU Minghu， FENG Qing， YANG Hongyi，

WEI Deng， YANG Xin

（

Department of Automation Engineering， Engineering & Technical College of Chengdu University of

Technology，

Leshan 200052， Sichuan， China）

Abstract：

To analyze the influence of the wheel-base and wheel-track design on the vehicle handling stability， the dynamic modelof vehicle steering on the transverse slope highway is established， and the corresponding simulation model is built in MATLAB/Simulink. The design values of wheel-base and wheel-track of the type of vehicle are used for simulation， and then the yaw rate， the lateral acceleration and the sideslip angle of the mass center are obtained while the vehicle steers on the highway with different transverse slopes at different speeds. The handling stability of the vehicle steering on the transverse slope highway is tested according to the steering characteristics and rollover threshold of the vehicle. The results show that the design values of wheel-base and wheel-track of the type of vehicle meet the handling stability. The calculation method and simulation results can guide the vehicle design direction.

Key words：

vehicle design; transverse slope; steer; yaw; sideslip; handling stability

0 引 言

近年來，汽車整車參數對操縱穩定性的影響越來越受到關注。王郭俊等[1]研究整車結構參數對雙半掛汽車操縱穩定性的影響;鄭希江等[2]研究前輪定位參數對汽車整車操縱穩定性的影響，并采用Adams進行仿真分析;蘭鳳崇等[3]根據車輪轉角研究整車操縱穩定性;邱衛明等[4]研究汽車橫向穩定桿剛度對汽車側傾角和整車操縱穩定性的影響;田萌健等[5]研究輪邊集成底盤系統新型懸架結構對整車操縱穩定性的影響;王基月等[6]研究車體質心位置變化對鉸接式自卸車操縱穩定性的影響;楊晨等[7]研究復合連桿式前懸架結構對自卸車操縱穩定性的影響;高晉等[8]研究副車架柔性參數對整車操縱穩定性的影響;杜錫滔等[9]研究彈簧剛度對整車操縱穩定性的影響。

在汽車整車設計過程中，軸距設計不當會使汽車操縱穩定性變差;同樣，輪距設計不當也會造成汽車橫向穩定性變差，甚至引起橫向坡道側翻。因此，應同時考慮軸距和輪距對汽車操縱穩定性的影響。汽車總體設計計算得到的軸距和輪距是否對汽車的操縱穩定性有不利影響，是一個值得考慮和分析的問題。通過樣車在專用試驗場的試驗進行汽車的操縱穩定性測試，然后根據測試結果修改總體設計中的參數。但是，這種多次樣車試驗和修改會導致設計成本和周期的增加。為解決這一問題，通常的做法是采用虛擬樣機技術建立汽車的仿真模型，通過仿真模型研究汽車的軸距和輪距是否對操縱穩定性產生不利的影響，提前預測汽車軸距和輪距的修改方向。

在汽車總體設計時建立相應的力學和數學模型，采用力學和物理參數以及整車設計尺寸參數描述整車及各系統，并使用MATLAB中的Simulink模塊對模型進行仿真，能夠降低設計成本并縮短開發周期。[10]近年來，類似的與橫向動力學相關的設計方法和理念研究較多。WARTH等[11]在MATLAB/Simulink中建立14自由度的非線性整車模型，論證其設計的控制器的有效性;RUBI-MASSEGU'等[12]運用仿真方法驗證其設計的懸架靜態輸出反饋控制器性能良好;JAVANSHIR等[13]對越野車懸架進行建模仿真并優化懸架幾何參數，根據仿真結果分析懸架幾何參數優化對越野車操縱穩定性的影響;AOUADJ等[14]設計車輛動力學控制系統，通過仿真證明該控制系統有效且有利于提高整車操縱穩定性;AHANGARNEJAD等[15]提出一種整車集成動力學系統，并通過仿真證明其有效性，認為與非集成系統相比，該系統能提高整車操縱穩定性指標;ASIABAR等[16]提出一種直接偏航力矩控制算法，并采用MATLAB/Simulink進行仿真，結果表明該方法能夠提高汽車操縱穩定性。

本文建立含軸距和輪距的整車數學模型，考慮汽車橫向坡道轉向行駛工況，通過模型仿真分析汽車總體設計中的軸距和輪距是否對操縱穩定性產生不利影響，從而預測總體設計中汽車軸距和輪距設計是否合理，以期縮短汽車設計周期、降低汽車的設計成本、提高設計效率。

1 汽車橫向坡道轉向行駛動力學模型

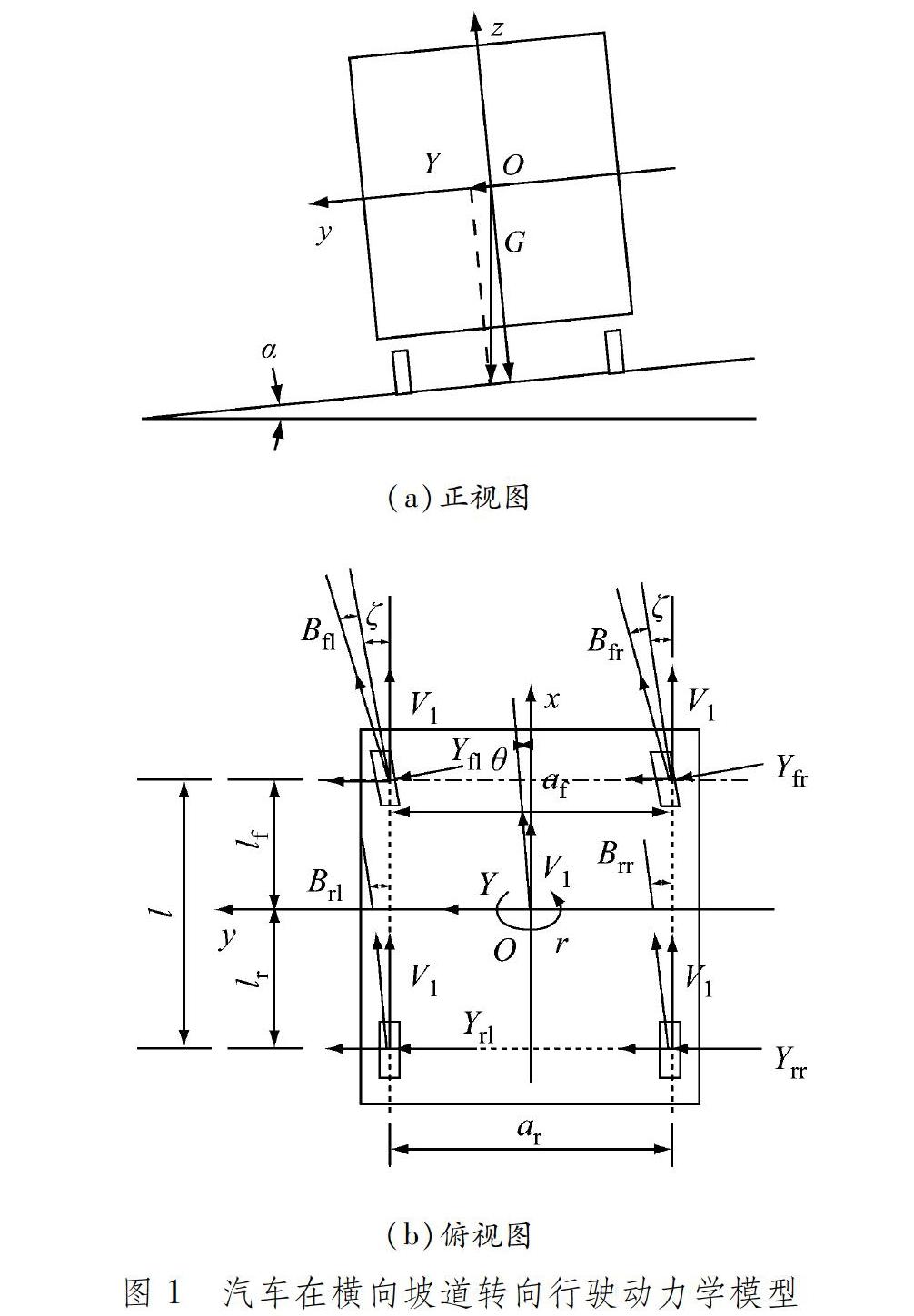
為分析汽車操縱穩定性，首先要建立相應的汽車動力學模型。[17]忽略汽車懸架彈性變形和輪胎垂直路面的彈性變形，只考慮汽車輪胎的彈性側偏;在汽車轉向運動中，忽略彈性元件、汽車零部件裝配間隙和柔性元件側傾導致的質心偏移。為便于排水或者為避免轉向運動產生離心力導致汽車側翻，高速公路在轉彎處要設立超高，即有橫向坡度。基于此，建立汽車在橫向坡道轉向行駛的動力學模型，見圖1，其中的符號含義及其量綱見表1，汽車轉向輪前面的虛線表示汽車轉向輪的航向即速度方向。

在汽車轉向行駛的過程中，由于汽車的橫擺運動和側向運動，在輪胎處產生彈性側偏，從而導致汽車的各車輪存在側偏角。按《公路工程技術標準》（JTG B01—2014）中的規定，超高值分別取0、6%和10%，對應的橫向坡道坡度α分別為0、3.43°和5.71°。設計車速分別為80、100和120 km/h，其中最低速度80 km/h是根據標準規定，在某些特定條件下由于地形特別復雜可以把高速公路的最低速度定為80 km/h。

2 汽車橫向坡道轉向行駛數學模型

根據汽車橫向坡道轉向行駛動力學模型建立數學模型。

汽車橫向坡道轉向行駛時，在過質心的橫向截面內，

Y=G sin α

（1）

4個車輪的側偏力計算公式分別為

Yfl=-γfBfl

（2）

Yfr=-γfBfr

（3）

Yrl=-γrBrl

（4）

Yrr=-γrBrr

（5）

汽車在橫向坡道上轉向運動時，汽車左、右轉向輪都存在轉向角ζ，ζ來自于轉向盤的轉角輸入。不考慮轉向系各元件的裝配間隙和彈性，可以近似地把轉向盤轉動角度輸入通過轉向系換算為汽車轉向輪的轉向角。由圖1可知，汽車轉向輪航向（即速度方向）與x軸（即汽車的縱軸方向）夾角也為ζ，ζ既是轉向輪的轉向角，也是汽車轉向輪速度方向與x軸的夾角，由此可以建立汽車4個車輪的側偏角的計算公式，即

Bfl≈V1θ+lfrV1-afr2-ξ

（6）

Bfr≈V1θ+lfrV1+afr2-ξ

（7）

Brl≈V1θ-lrrV1-arr2

（8）

Brr≈V1θ-lrrV1+arr2

（9）

式中：V1θ為汽車轉向輪速度在x軸方向的分量;afr/2、arr/2分別為汽車轉向輪速度在汽車前、后輪橫向即y軸方向的分量。

將式（6）～（9）分別代入式（2）～（5），可得到汽車4個車輪的側偏力分別為

Yfl=-γfV1θ+lfrV1-afr2-ξ

（10）

Yfr=-γfV1θ+lfrV1+afr2-ξ

（11）

Yrl=-γrV1θ-lrrV1-arr2

（12）

Yrr=-γrV1θ-lrrV1+arr2

（13）

式（10）～（13）中同時包含軸距和輪距2個參數。分析圖1可知，Yff、Yfr、Yrl和Yrr均作用于輪胎且方向基本垂直于汽車航向，即與汽車橫向y軸方向基本一致。同時，汽車在橫向坡道上行駛，汽車受到的重力在過質心的橫向截面內的分力Y也與汽車航向基本垂直，即與汽車橫向y軸方向基本一致。Y即為汽車橫向坡道轉向行駛時對汽車操縱穩定性的側向干擾力。汽車操縱穩定性可以分別用質心側偏角和橫擺角速度響應評價。[18]由此，建立汽車側向（橫向）運動方程，即

mV1dθdt+r=Yff+Yfr+Yrl+Yrr+Y

（14）

Y作用在汽車質心上，不會產生繞坐標系z軸的轉動力矩，而Yff、Yfr、Yrl和Yrr會產生作用在汽車上的繞坐標系z軸的轉動力矩，由此建立汽車橫擺運動方程，即

Izdrdt=lf（Yfl+Yfr）-lr（Yrl+Yrr）

（15）

式中：Iz為汽車繞z軸的轉動慣量。

將式（1）和式（10）～（13）分別代入式（14）和（15）中，可得

mV1dθdt+r=-γfV1θ+lfrV1-afr2-ξ-γfV1θ+lfrV1+afr2-ξ-γrV1θ-lrrV1-arr2-γrV1θ-lrrV1+arr2+Gsin α

（16）

Izdrdt=lf-γfV1+lfrV1-afr2-ξ-γfV1θ+lfrV1+afr2-ξ-lr-γrV1θ-lrrV1-arr2-γrV1θ-lrrV1+arr2

（17）

式（16）和（17）即為描述汽車在橫向坡道上轉向行駛的數學模型。由此可知，當轉向輪輸入任意轉向角度ζ時，汽車的運動與地面坐標系的位置和汽車航向無關。汽車的軸距、輪距、質量、輪胎的側偏剛度，以及高速公路的橫向坡度均影響汽車的運動。汽車質心側偏角θ、橫擺角速度r導致汽車產生轉向角ζ[19]，因此θ和r是評價汽車操縱穩定性的主要參數[20]。

3 汽車穩態轉向特性

在汽車穩態轉向行駛時，汽車質心側偏角和橫擺角速度不變，即dθ/dt=0、dr/dt=0。為計算方便，將式（16）和（17）適當簡化，則轉向半徑為

ρ=1-m（lfγf-lrγr）V212l2γfγr1ζ

（18）

若ζ為定值，則有：當lfγf-lrγr<0時，ρ隨V1增大而減小，汽車呈現不足轉向的特性;當lfγf-lrγr>0時，ρ隨V1增大而增大，汽車呈現過度轉向的特性;當lfγf-lrγr=0時，ρ不隨V1變化，汽車呈現中性轉向的特性。某車型設計參數見表2。

根據表2計算可知該型汽車lfγf-lrγr<0，即有不足轉向的特性。

該車型特征車速為

Vch=-mI2afγr-arγf-[SX（]12[SX）]

（19）

根據表2可計算得到Vch=50 km/h，當車速大于50 km/h時，質心側偏角隨速度增加而減小。

4 汽車在橫向坡道行駛的側翻閾值

輪距減小使側翻阻力減小，從而導致行駛不穩定。較寬的輪距能加強汽車的橫向穩定性和抗側翻能力。[21]

汽車側翻時的動力學模型見圖2，其中：ay為側向加速度，ay方向平行于橫向坡道坡面;h為汽車質心到橫向坡道坡面的垂直距離;Fi和Fo分別為橫向坡道坡面對左、右汽車輪胎的支承反力，方向垂直于橫向坡道坡面;Yfl、Yrl、Yfr、Yrr為汽車輪胎所受的側偏力，方向與橫向坡道坡面平行。汽車左轉向行駛時的側向加速度為

假定汽車為只含輪胎彈性側偏的近似剛體，那么汽車在橫向坡道轉向行駛時無質心的偏移，因此不用考慮車輛的橫向載荷轉移率。基于該假定分析汽車在橫向坡道轉向行駛時側向加速度與汽車側翻的關系。

當汽車在橫向坡道穩定左轉向時，隨著車速增大，

ay增大直至Fi為0，此時汽車輪胎剛好離開坡面，汽車將要發生側翻。以右側車輪與地面接觸點為原點建立數學模型，即

mayh-mghsin α+Fiar-12mgarcos α=0

（21）

當Fi=0時，上式變為

ay=gsin α+argcos α2h

（22）

若取超高值為10%，則橫向坡度α約為5.71°，此時sin α=0.099 49、cos α=0.995 00，取h=0.5 m、ar=1.5 m代入式（21）得ay=16.41 m/s2，ay值即為該車型在坡度為5.71°的橫向坡道轉向行駛時的側翻閾值。如果該型汽車在橫向坡道轉向行駛的側向加速度值大于所求的側翻閾值，該型汽車將側翻。為避免汽車側翻，橫向加速度必須小于側翻閾值。[22]由于本文將汽車假定為近似剛體，所以求出的側翻閾值偏大，但仍可以作為仿真計算的參考值。同理，橫向坡道

坡度為3.43°對應的側翻閾值為15.52 m/s2。

5 汽車橫向坡道轉向行駛仿真

5.1 建立仿真模型

MATLAB是一款功能強大的應用軟件，其Simulink工具箱可以獲得可視化數據并用于分析，方便快捷。根據式（16）和（17），運用Simulink工具箱構建汽車橫向坡道轉向行駛仿真模型。

5.2 仿真分析數據和轉向輪轉向角輸入

Simulink建模仿真數據取表2中某車型設計參數，

研究該型汽車在不同橫向坡度的道路上以不同車速行駛時的操縱穩定性，從而分析該車型的軸距和輪距對操縱穩定性的影響，判斷該車型的軸距和輪距設計是否滿足汽車操縱穩定性要求。

角階躍輸入試驗是道路試驗中最典型的試驗[23]，汽車對轉向盤輸入的瞬態響應能夠通過階躍試驗反映[24]。本文仿真采用轉向盤的角階躍輸入換算為轉向輪的轉向角階躍輸入。

5.3 轉向輪的角階躍輸入final值為定值的仿真結果

轉向輪轉向角階躍輸入時間為10.0 s。汽車的轉向盤存在自由行程，因此轉向輪的轉向角階躍輸入的initial值在0.5 s前為0，階躍輸入的final值為0.010 rad。

對該型汽車在橫向坡度為0、3.43°和5.71°的坡道上分別以80、100和120 km/h速度轉向行駛進行仿真，轉向輪轉向角階躍輸入曲線見圖3。

汽車以不同速度在不同橫向坡度道路上轉向行駛時的橫擺角速度、質心側偏角和側向加速度仿真結果見圖4和5。

6 仿真結果分析

根據仿真結果可知，當階躍輸入的final值為0.010 rad時，該型汽車以不同速度在不同橫向坡度道路上轉向行駛的側向加速度峰值和穩定值均小于該車在相應橫向坡度的側翻閾值，這意味著該型汽車在此階躍輸入下不會發生側翻。

6.1 0～0.5 s時間段內的仿真結果分析

在0～0.5 s時間段內，該型汽車轉向輪轉向角階躍輸入initial值為0，汽車在3.43°和5.71°坡度的橫向坡道行駛時受到作用于汽車質心的側向力Y

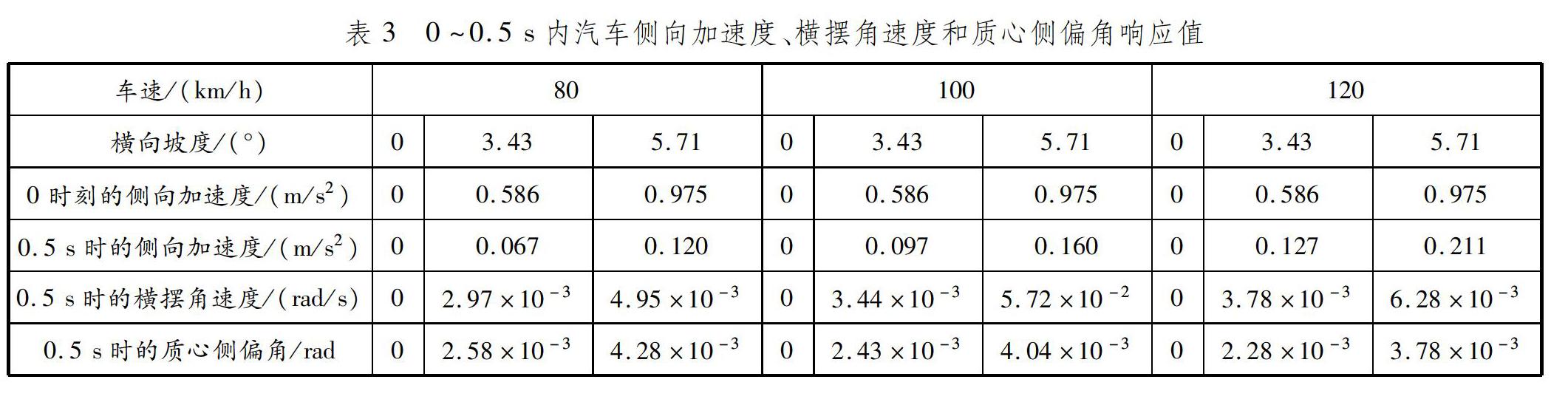
而產生側向運動，同時該型汽車質心產生側偏角，汽車輪胎受到側偏力作用。該型汽車在0～0.5 s仿真時間段內的側向加速度、橫擺角速度和質心側偏角響應值見表3。

作用于質心的側向力Y導致汽車的側向加速度在0～0.5 s時間段內迅速減小。隨著車速和坡度的增大，側向加速度在0.5 s時也減小。進一步仿真該型汽車在橫向坡度為3.43°和5.71°工況下無轉向行駛的情況，結果在0.5 s時其側向加速度穩態值達到最小，表明該型汽車在無轉向角輸入時橫向穩定性較好。在0時刻以及橫向坡度為0時，質心側偏角、橫擺角速度都為0。在橫向坡度為3.43°和5.71°時，由于側向力Y的作用，汽車產生側向運動，質心側偏角和橫擺角速度隨時間增加而增大。在0.5 s時質心側偏角、橫擺角速度達到最大。0.5 s時的質心側偏角、橫擺角速度最大值隨橫向坡度和速度增大而減小，說明該型汽車在橫向坡道轉向行駛時操縱穩定性較好。

6.2 0.5～10.0 s時間段內的仿真結果分析

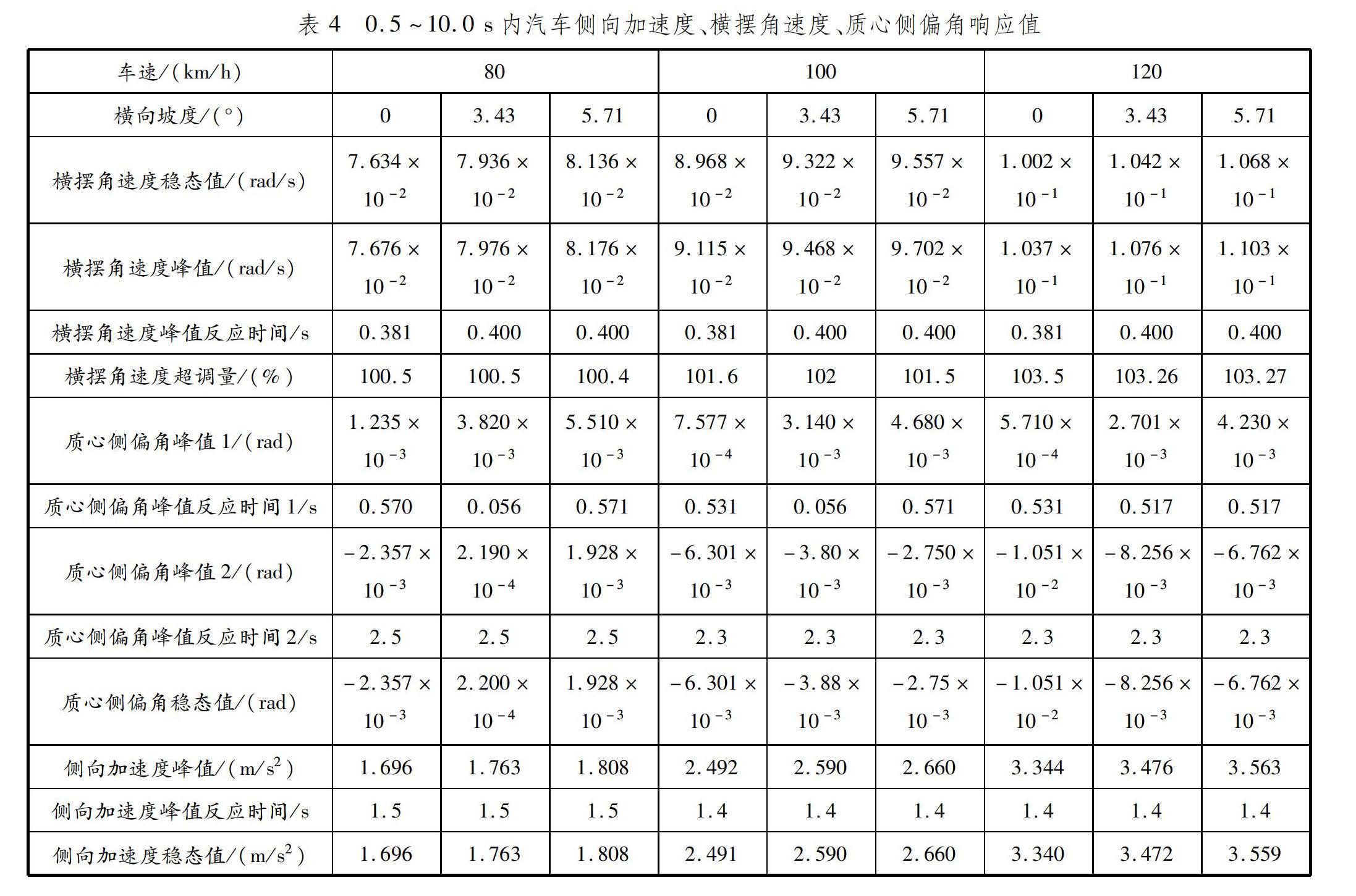
在0.5～10.0 s時間段內汽車的側向加速度、橫擺角速度和質心側偏角響應值見表4。

該型汽車在不同橫向坡度道路以不同速度轉向行駛時的橫擺角速度超調量最大為103.27%，最小為100.5%，超調量較小且變化不大，說明該型汽車能

夠迅速從橫擺角速度峰值回到穩定狀態，汽車操縱穩定較好。橫擺角速度和側向加速度各自的峰值響應時間也能夠反映汽車對操縱響應的靈敏程度。[25]質心側偏角和側向加速度峰值時間均較小，說明該型汽車瞬態響應迅速、操縱靈敏。

從前文可知，該型汽車具有不足轉向特性，特征速度Vch=50 km/h。仿真車速80、100和120 km/h均大于特征速度Vch，故該型汽車質心側偏角穩態值在同一橫向坡度上隨速度的增加而減小，直至為負值。在車速120 km/h、橫向坡度為5.71°時，質心側偏角達到-6.762×10-3 rad。當該型汽車以同一速度在不同橫向坡度道路上轉向行駛時，側向力Y的大小隨橫向坡度變化而變化，橫向坡度為5.71°時Y最大。當該型汽車以同一速度在不同橫向坡度的道路上行駛時，Y與車輪的側偏力共同平衡離心力，質心側偏角隨橫向坡度的增加而減小。在橫向坡度為5.71°時質心側偏角最小，說明該車型在橫向坡道行駛時操縱穩定性較好。汽車的側向力越大，汽車抵抗干擾的能力越強，側向偏移越小。[26]該型汽車側向加速度穩定值隨橫向坡度和速度的增大而增大，側向加速度穩態值小于側翻閾值，也說明該車型橫向穩定性好。

7 結束語

建立考慮某設計車型橫向坡道轉向行駛的動力學模型及其相應的數學模型，并根據該車型的設計軸矩和輪距進行仿真計算，得到該設計車型以80、100和120 km/h的速度分別在橫向坡度為0、3.43°和5.71°的道路上轉向行駛時的側向加速度、橫擺角速度和質心側偏角響應值，結果表明該車型的在橫向坡道上轉向行駛的操縱穩定性較好，該車型的軸距和輪距設計均可以滿足要求。

參考文獻：

[1]

王郭俊， 許洪國， 劉宏飛. 雙半掛汽車列車操縱穩定性分析[J]. 浙江大學學報（工學版）， 2019， 53（2）： 299-306.

[2] 鄭希江， 紀少波， 李淑廷， 等. 獨立懸架前輪定位參數對操縱穩定性影響分析[J]. 機械設計與制造， 2019（7）： 263-267.

[3] 蘭鳳崇， 李詩成， 陳吉清， 等. 考慮操縱穩定性的自動駕駛汽車軌跡綜合優化方法[J]. 湖南大學學報（自然科學版）， 2019， 46（10）： 36-45. DOI： 10.16339/j.cnki.hdxbzkb.2019.10.005.

[4] 邱衛明， 祝書偉. 橫向穩定桿剛度對乘用車操縱穩定性的影響研究[J]. 機電工程， 2019， 36（7）： 744-748. DOI： 10.3969/j.issn.1001-4551.2019.07.017.

[5] 田萌健， 李偉鋒， 孟德樂， 等. 面向機動性與操縱穩定性的輪邊集成底盤系統設計[J]. 機械工程學報， 2019， 55（22）： 11-20.

[6] 王基月， 李偉. 鉸接式自卸車操縱穩定性影響因素分析[J]. 機械設計與制造， 2018（7）： 180-183.

[7] 楊晨， 張曉瑩. 基于在環試驗自卸車懸架系統操縱穩定性分析[J]. 機械設計與制造， 2018（6）： 207-211.

[8] 高晉， 艾田付， 李芷昕， 等. 副車架柔性對整車操縱穩定性能影響的研究[J]. 昆明理工大學學報（自然科學版）， 2018， 43（6）：118-123. DOI： 10.16112/j.cnki.53-1223/n.2018.06.016.

[9] 杜錫滔， 熊銳， 吳堅， 等. 基于車輛操縱穩定性及平順性的底盤多目標優化[J]. 現代制造工程， 2018（5）： 98-101. DOI： 10.16731/j.cnki.1671-3133.2018.05.018.

[10] 李杰， 高雄， 王維， 等. 基于UniTire模型的平順性和操縱穩定性協同研究[J]. 汽車工程， 2018， 40（2）： 127-132. DOI： 10.19562/j.chinasae.qcgc.2018.02.001.

[11] WARTH G， FREY M， GAUTERIN F. Design of a central feedforward control of torque vectoring and rear-wheel steering to beneficially use tyre information[J]. Vehicle System Dynamics， 2020， 58（12）： 1789-1822. DOI： 10.1080/00423114.2019.1647345.

[12] RUBI-MASSEGU' J， PALACIOS-QUIONERO F， ROSSELL J M， et al. Static output-feedback controller design for vehicle suspensions： An effective two-step computational approach[J]. IET Control Theory & Applications， 2014， 8（15）： 1566-1574. DOI： 10.1049/iet-cta.2013.1129.

[13] JAVANSHIR I， MASELENO A， TASOUJIAN S， et al. Optimization of suspension system of heavy off-road vehicle for stability enhancement using integrated anti-roll bar and coiling spring mechanism[J]. Journal of Central South University， 2018， 25（9）： 2289-2298. DOI： 10.1007/s11771-018-3913-6.

[14] AOUADJ N， HARTANI K， FATIHA M. New integrated vehicle dynamics control system based on coordination of active front steering， direct yaw control， and electric differential for improvements in vehicle handling and stability[J]. SAE International Journal of Vehicle Dynamics， Stability， and NVH-V129-10EJ， 2020， 4（2）： 119-133. DOI： 10.4271/10-04-02-0009.

[15] AHANGARNEJAD A H， MELZI S， AHMADIAN M. Integrated vehicle dynamics system through coordinating active aerodynamics control， active rear steering， torque vectoring and hydraulically interconnected suspension[J]. International Journal of Automotive Technology， 2019， 20（5）： 903-915. DOI： 10.1007/s12239-019-0084-x.

[16] ASIABAR A N， KAZEMI R. A direct yaw moment controller for a four in-wheel motor drive electric vehicle using adaptive sliding mode control[J]. Proceedings of Institution of Mechanical Engineers， Part K： Journal of Multi-body Dynamics， 2019， 233（3）： 549-567. DOI： 10.1177/1464419318807700.

[17] 潘公宇， 張明梅. 高速轉向工況下汽車操縱穩定性和平順性研究[J]. 廣西大學學報（自然科學版）， 2016， 41（3）： 674-683. DOI： 10.13624/j.cnki.issn.1001-7445.2016.0674.

[18] KHAN M M， AWAN A U， LIAQUAT M. Improving vehicle handling and stability under uncertainties using probabilistic approach[J]. International Federation of Automatic Control， 2015， 48（25）： 242-247. DOI： 10.1016/j.ifacol.2015.11.094.

[19] 劉文營， 劉偉， 崔曉川. 二自由度車輛動力學模型的擴展研究[J]. 中國測試， 2016， 42（S2）： 76-79.

[20] 劉秋生， 徐延海， 陳啟. 4WID輪轂電機式電動汽車橫擺穩定性滑模控制研究[J]. 廣西大學學報（自然科學版）， 2015， 40（5）： 1080-1091. DOI： 10.13624/j.cnki.issn.1001-7445.2015.1080.

[21] HASSAN M A， ABDELKAREEM M A A， MOHEYELDEIN M M， et al. Advanced study of tire characteristics and their influence on vehicle lateral stability and untripped rollover threshold[J]. Alexandria Engineering Journal， 2020， 59（3）： 1613-1628. DOI： 10.1016/j.aej.2020.04.008.

[22] CHOKOR A， TALJ R， DOUMIATI M， et al. A global chassis control system involving active suspensions， direct yaw control and active front steering[J]. International Federation of Automatic Control， 2019， 52（5）： 444-451. DOI： 10.1016/j.ifacol.2019.09.071.

[23] 張洪昌， 丁建完. 基于Modleica的操縱穩定性實時仿真方法研究[J]. 計算機工程與應用， 2015， 51（3）： 31-34. DOI： 10.3778/j.issn.1002-8331.1407-0098.

[24] 陳煥明， 郭孔輝. 輪胎性能對車輛操縱穩定性影響的仿真研究[J]. 汽車工程， 2015， 37（5）： 491-494. DOI： 10.19562/j.chinasae.qcgc.2015.05.001.

[25] 徐剛， 龐赟， 周毅， 等. 輪轂電機對汽車瞬態操縱穩定性的影響[J]. 計算機輔助工程， 2016， 25（4）： 29-32. DOI： 10.13340/j.cae.2016.04.006.

[26] 李洋， 張建偉， 郭孔輝， 等. 四輪驅動電動汽車軸間驅動力和制動力分配[J]. 吉林大學學報（工學版）， 2015， 45（3）： 703-710. DOI： 10.13229/j.cnki.jdxbgxb201503004.

（編輯 武曉英）