基于反應擴散方程的水平集結構拓撲優化方法與實現

賴松 王坤

摘要：為實現更加先進的拓撲優化算法，研究采用反應擴散方程的水平集結構拓撲優化方法，通過理論推導給出算法中的參數選擇建議。該方法允許在拓撲優化過程中生成新的孔洞，初始結構無須包含孔洞，不需要重新初始化步驟，從而可提高算法的收斂性。針對傳統拓撲優化中主要采用體積約束、以柔度最小為目標和體積保留率設定存在一定主觀性的問題，探究不同體積保留率下的結構應力水平的變化規律，結果顯示可以依據結構最大應力水平與體積保留率的變化規律確定最優體積保留率。

關鍵詞：

反應擴散方程; 水平集; 拓撲優化; 體積保留率; 收斂

中圖分類號：TB115.2

文獻標志碼：B

Topology optimization method and its implement of

level set structure using reaction diffusion equation

LAI Song， WANG Kun

（School of Energy and Power Engineering， Huazhong University of Science and Technology， Wuhan 430064， China）

Abstract：

To realize a more advanced topology optimization algorithm， the level set structure topology optimization method using reaction diffusion equation is studied. The parameter selections in the algorithm are suggested by theoretical deduction. In this method， the generation of new holes in the process of topology optimization is allowed， and the initial structure does not need to set holes， and the initialization step need not restart， and then the convergence of the algorithm can be improved. In traditional topology optimization， the constraint is volume， and the objective is minimum flexibility， and the setting of volume retention rate is subjective. As to this issue， the variation law of structural stress level under different volume retention rate is explored. The results show that the optimal volume retention rate can be determined according to the variation law of the maximum stress level and volume retention rate of the structure.

Key words：

reaction diffusion equation; level set; topology optimization; volume retention rate; convergence

0 引 言

拓撲優化方法是在給定設計域中確定材料的分布、形狀和連通性以達到某一最優目標的方法。[1]與尺寸優化和形狀優化相比，拓撲優化有更大的設計自由度，因此可用于在概念設計階段產生最佳的拓撲結構，進而得到可觀的經濟收益。在最近幾十年里，結構拓撲優化取得長足發展，以變密度法為代表的拓撲優化方法廣泛應用于結構、傳熱、流動和多物理場等領域。拓撲優化模塊已經嵌入到某些商業有限元軟件中，并應用于實際工程中。[2]在眾多的拓撲優化方法中，最常見的是變密度法和水平集法。變密度法引入一個在0～1范圍內連續變化的虛擬密度，并以此作為設計變量，表示材料的有無。由于虛擬密度是連續的，可以視作普通的場變量，所以變密度法與現有成熟的有限元法耦合良好。變密度法可以利用懲罰機制減少中間密度單元，但是無法得到真正的“0-1”分布，所以可能會在考慮材料非線性、應力約束等情況下出現問題。水平集法采用零水平集函數顯式地表示結構邊界，因此可以得到“0-1”分布，特別適用于考慮邊界的拓撲優化。水平集方法的缺陷是過度依賴初始結構、迭代過程受限于時間步長、優化過程更加復雜等。

以柔度最小為目標的優化問題一般都具有良好的數學性質，因此大多數結構拓撲優化算法均以柔度最小為目標。但是，在實際工程結構設計中，有時工程師更看重的設計目標是強度。目前，與應力相關的優化目標在結構拓撲優化設計中還存在一定的困難。[3]一方面，應力的局部性質要求約束必須作用在每一個材料點上，導致約束的量非常大;另一方面，在基于密度的方法中，密度非常低的單元反而可能會出現較高的應力值，即應力奇異現象。

針對第一個問題，常見的解決方案是通過一個全局應力函數將大量局部應力約束擬合成一個全局約束，常見的全局函數有p-范數函數和K-S函數。LE等[4]將分區域的全局應力約束函數和自適應正則化方案相結合，在一定程度上可緩解應力集中現象。XIA等[5]提出改進的p-范數全局應力函數以控制最大應力，該全局函數可節約大量計算資源，但有時不能完全估計結構的局部應力特征，無法起到控制最大應力的作用。CHEN等[6]發現某些實際工程中使用最大主應力失效準則而不是VON MISES應力準則，因此將最大主應力作為約束，采用BESO作為優化求解器進行計算。EMMENDIERFER等[7]使用與SIMP法一樣的應力松弛、p-范數聚集等技術，研究柔性機構的應力約束優化問題。PICELLI等[8]通過在每個迭代步中求解一個子問題得到優化的邊界速度場，算例顯示優化后的結構有非常平滑的邊界。LIAN等[9]基于DSC方法更新網格，結合形狀和拓撲優化解決最大VON MISES應力問題。

針對第二個問題，利用應力松弛方法，如qp-松弛法[3]、插值函數懲罰法[4，10]，可以消除應力奇異現象。但是，由于應力與結構的強非線性相關性，在尖角、孔洞和邊界處會出現應力集中現象[11]，極易導致拓撲優化出現不穩定、收斂困難甚至無法收斂等問題。盡管如此，在工程應用中基于應力約束的拓撲優化方法只能應用于一些簡單的結構，如板、殼、桿和混凝土結構等，而數學性質更好的柔度最小化目標仍然是更廣泛使用的模型。

鑒于應力問題的復雜性，本文以結構柔度最小為優化目標，研究基于反應擴散方程的水平集結構拓撲優化方法，并考察方法中各參數對優化迭代過程與拓撲結構的影響。在不同體積約束下對下承式橋梁進行優化，分析得到結構應力與體積保留率的變化規律及其適用條件。

1 拓撲優化問題

1.1 基于水平集的拓撲結構描述

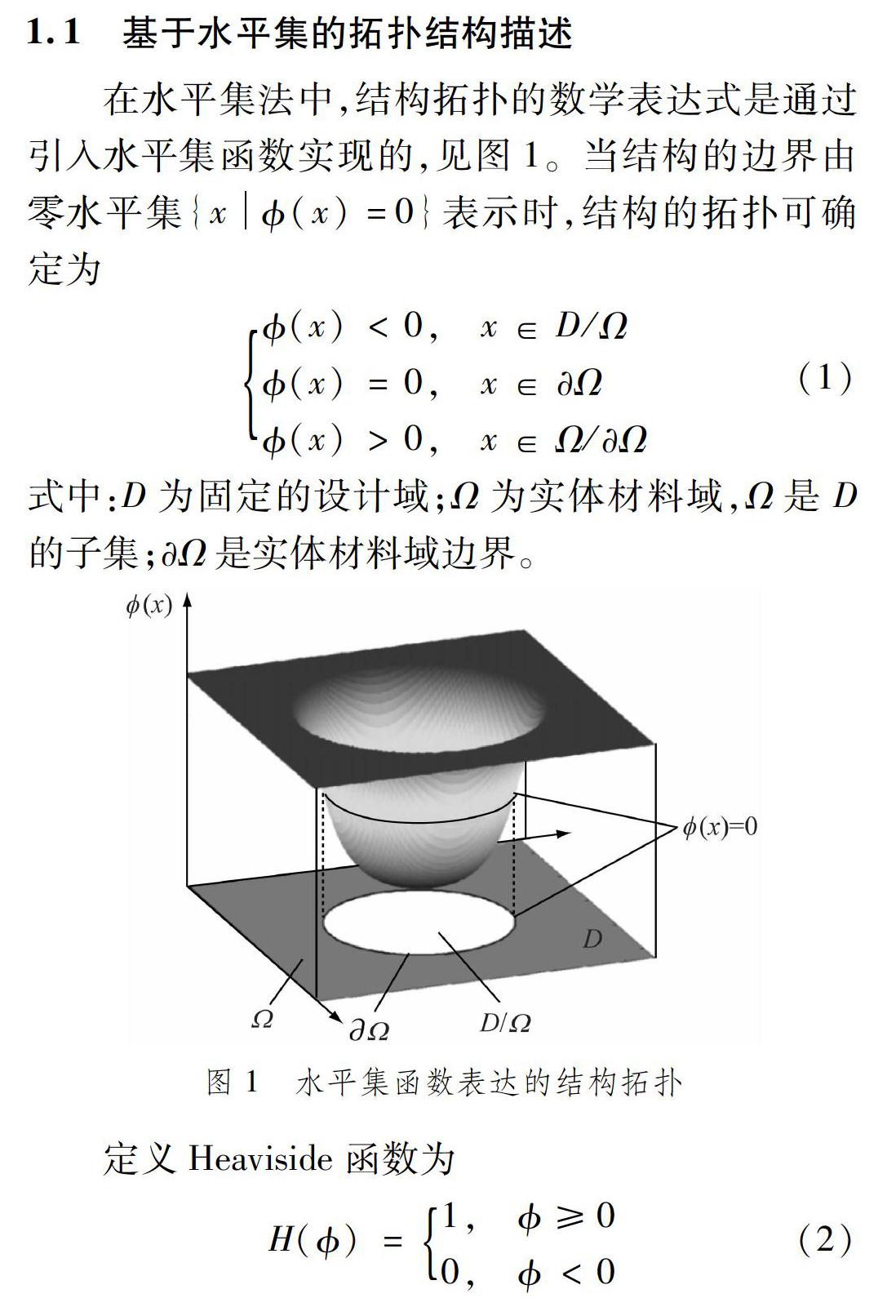
在水平集法中，結構拓撲的數學表達式是通過引入水平集函數實現的，見圖1。當結構的邊界由零水平集{x（x）=0}表示時，結構的拓撲可確定為

（x）<0， x∈D/Ω

（x）=0， x∈Ω

（x）>0， x∈Ω/Ω

（1）

式中：D為固定的設計域;Ω為實體材料域，Ω是D的子集;Ω是實體材料域邊界。

定義Heaviside函數為

H（）=1， ≥0

0， <0

（2）

實體材料域Ω可以表示為

Ω={x|H（（x））=1}

（3）

2.2 結構場控制方程

假設實體域材料為各向同性線彈性材料，線彈性結構的微分控制方程為

-div（σ（u））=0，u∈Ω

u=0，u∈ΓD

σ（u）n=t，u∈ΓN

（4）

式中：u為位移場變量;ΓD為狄利克雷邊界;ΓN為紐曼邊界;t為作用在紐曼邊界上的載荷，在本文中是一個常量，不隨優化進程變化;σ（u）為應力張量，其定義為

σ（u）=Cε（u）

（5）

ε（u）=12（SymbolQC@u+（SymbolQC@u）T）

（6）

式中：C為彈性張量;ε（u）為應變張量。

2.3 柔度最小優化問題

優化目標為柔度最小，約束為體積約束，即

min J（u）=∫Ω（ε（u））TCε（u）dV

s.t. G（Ω）=∫ΩdV-V∫DdV=0

（7）

式中：V為給定的體積保留率。

2.5 增廣拉格朗日乘子法

增廣拉格朗日乘子法是大多數水平集法使用的優化算法，能將優化問題（式（7））轉化為無約束問題并求解。增廣拉格朗日函數定義為

L（u，λ，η）=J（u）+λG（Ω）+η2（G（Ω））2

（8）

式中：η為懲罰因子，在本文中，懲罰因子在整個迭代過程保持不變;λ為拉格朗日乘子，其更新方案為

λk+1=λk+ηG（Ω）

（9）

3 水平集函數更新

3.1 反應擴散方程

傳統的水平集函數更新Hamilton-Jacobi方程無法生成孔洞，需要重新初始化步驟。為避免這一問題，可使用基于反應擴散方程的水平集更新方式[12]，即

t=αSymbolQC@2+Vn，∈D

（t=0）=0，∈D∪D

n=0，∈D/DN

=1，∈DN

（10）

式中：α為擴散系數;Vn為法向速度場;αSymbolQC@2為擴散項;DN為非設計域的邊界。αSymbolQC@2可增加拓撲優化問題的正則性，促進水平集函數更新過程的穩定性，所以上式可以用標準伽遼金有限元法離散求解，以簡化有限元法求解水平集方程的過程。此外，擴散項使形狀靈敏度更加平滑，因此調整擴散系數α可以控制拓撲結構的復雜度，但擴散項有時也令靈敏度過于平坦，從而導致收斂出現問題，應綜合考慮。

3.2 法向速度場的計算

法向速度場Vn可為水平集函數更新提供最高速下降方向，由增廣拉格朗日函數的形狀靈敏度求得。形狀靈敏度反映邊界移動對目標函數的影響，可以由物質導數公式和伴隨方法[13]推導得到。

柔度目標的形狀靈敏度為

δJδ=∫Ω（-（ε（u））TCε（u））VndΓ

（11）

體積約束的形狀靈敏度為

δGδ=∫ΩVndΓ

（12）

因此

δLδ=∫Ω（-（ε（u））TCε（u）+λ+ηG（Ω））VndΓ

（13）

法向速度場為

Vn=V0-λ-ηG（Ω）

（14）

其中

V0=（ε（u））TCε（u）

（15）

4 數值實現

為能夠在固定網格中運用有限元法求解位移場，位移場必須在整個設計域中都有定義，而不只是存在于實體材料域中。為將位移場拓展到整個設計域，使用彈性模量非常小的弱材料填充無材料區域D-Ω，避免整體剛度矩陣奇異。參照變密度法，采用虛擬密度ρ表示有限元單元的材料屬性（有或無），因此材料的彈性模量Eρ可表示為

Eρ=Emin+ρ（E-Emin）

（16）

式中：E為實體材料的彈性模量;Emin為弱材料的彈性模量，一般取Emin=E×10-3。

2種方法的迭代曲線見圖8。變密度法收斂只迭代64次，而水平集法迭代168次才收斂，說明變密度法的收斂過程在穩定性和速度方面要優于水平集法。因此，水平集法仍然需要在算法方面進一步研究以提高其穩定性和效率。

5.3 不同體積保留率V下最優結構的最大等效應力變化規律

以某橋梁模型拓撲優化為例，其初始結構見圖9（a），尺寸為10 m×4 m×4 m，橋梁下底面兩端固定，橋面施加10 N/m2方向向下的面載荷。橋面以下的區域為非設計域，占總體積的6.25%。不同體積保留率下的優化結果分別見圖9（b）～（d）。

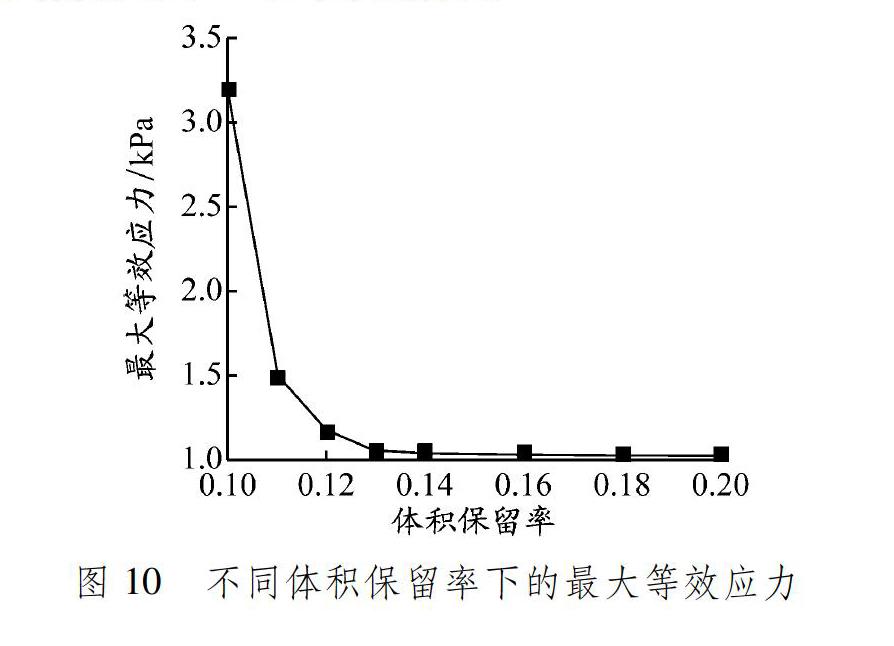
不同體積保留率V下優化結構的最大應力見圖10。由此可知：隨著V增大，優化結果的最大等效應力一直減小;當V<0.12時，最大等效應力隨V的減小迅速增大;當V>0.12時，最大等效應力減小幅度不大。這是因為隨著體積分數的減小，一些加強性結構被刪除，導致結構拓撲發生較大的改變，從而造成最大等效應力迅速增大。V越小優化越困難，所花費的時間越多，因此V不應過小，在本文模型中最佳的V為0.12。因此，針對具體的優化問題，體積保留率應該存在一個最佳值，可以使材料消耗與結構應力處于最優搭配。

6 結束語

針對以柔度最小為目標的結構優化問題，實現基于反應擴散方程的水平集法，重點考察時間步長和水平集方程求解次數這2個影響參數，結果認為水平集法的時間步長不受CFL條件限制，無論時間步長為何值，都能得到穩定的優化結果。然而，總時間步長（即時間步長與求解次數的乘積）過大會使優化結構更加簡單。當總時間步長一定時，適當增加水平集求解次數可以減少迭代次數、節約時間。將基于反應擴散方程的水平集法與變密度法進行對比，水平集法能夠得到更清晰的邊界結構，能夠調節結構復雜度但收斂緩慢。根據不同體積保留率下最優結構的最大等效應力變化規律可知，針對具體的優化問題，體積保留率應該存在一個最佳值，可以使材料消耗與結構應力處于最優搭配，該值可以通過考察體積保留率與最大應力或結構柔度之間的變化規律獲得。

參考文獻：

[1] VAN DIJK N P， MAUTE K， LANGELAAR M， et al. Level-set methods for structural topology optimization： A review[J]. Structural and Multidisciplinary Optimization， 2013， 48（3）： 437-472. DOI： 10.1007/s00158-013-0912-y.

[2] 張召穎， 張帆， 鄒洵， 等. 基于Ansys Workbench的T形結構優化設計[J]. 計算機輔助工程， 2019， 28（3）： 35-38. DOI： 10.13340/j.cae.2019.03.007.

[3] DUYSINX P， BENDSE M P. Topology optimization of continuum structures with local stress constraints[J]. International Journal for Numerical Methods in Engineering， 1998， 43（8）： 1453-1478. DOI： 10.1002/（SICI）1097-0207（19981230）43：8〈1453：：AID-NME480〉3.0.CO;2-2.

[4] LE C， NORATO J， BRUNS T， et al. Stress-based topology optimization for continua[J]. Structural and Multidisciplinary Optimization， 2010， 41（4）： 605-620. DOI： 10.1007/s00158-009-0440-y.

[5] XIA Q， SHI T L， LIU S Y， et al. A level set solution to stress-based structural shape and topology optimization[J]. Computers & Structures， 2012， 90/91： 55-64. DOI： 10.1016/j.compstruc.2011.10.009.

[6] CHEN A B， CAI K， ZHAO Z L， et al. Controlling maximum first principal stress in topology optimization[J]. Structural and Multidisciplinary Optimization， 2020， 63： 327-339. DOI： 10.1007/s00158-020-02701-5.

[7] EMMENDIERFER H， FANCELLO E A， SILVA E C N. Stress-constrained level set topology optimization for compliant mechanisms[J]. Computer Methods in Applied Mechanics and Engineering， 2020， 362： 112777. DOI： 10.1016/j.cma.2019.112777.

[8] PICELLI R， TOWNSEND S， BRAMPTON C， et al. Stress-based shape and topology optimization with level set method[J]. Computer Methods in Applied Mechanics and Engineering， 2018， 329： 1-23. DOI： 10.1016/j.cma.2017.09.001.

[9] LIAN H J， CHRISTIANSEN A N， TORTORELLI D A， et al. Combined shape and topology optimization for minimization of maximal VON MISES stress[J]. Structural and Multidisciplinary Optimization， 2017， 55（5）： 1541-1557. DOI： 10.1007/s00158-017-1656-x.

[10] 占金青， 龍良明， 劉敏. 熱彈性結構全局應力約束拓撲優化設計[J]. 機械科學與技術， 2019， 38（9）： 1386-1392. DOI： 10.13433/j.cnki.1003-8728.20190005.

[11] 張維生. 基于水平集方法的應力相關拓撲優化問題研究[D]. 大連： 大連理工大學， 2013.

[12] YAMADA T， IZUI K， NISHIWAKI S， et al. A topology optimization method based on level set method incorporating a fictitious interfaceenergy[J]. Computer Methods in Applied Mechanics and Engineering， 2010， 199（45-48）： 2876-2891. DOI： 10.1016/j.cma.2010.05.013.

[13] ALLAIRE G， JOUVE F， TOADER A M. Structural optimization using sensitivity analysis and a level-set method[J]. Journal of Computational Physics， 2004， 194（1）： 363-393. DOI： 10.1016/j.jcp.2003.09.032.

[14] ANDREASSEN E， CLAUSEN A， SCHEVENELS M， et al. Efficient topology optimization in MATLAB using 88 lines of code[J]. Structural and Multidisciplinary Optimization， 2011， 43（1）： 1-16. DOI： 10.1007/s00158-010-0594-7.

（編輯 武曉英）