多旋翼飛行器建模與控制器設計

杜 明，趙燕飛，范書瑞，賈穎淼，吳佳飛

(1.中國電子科技集團公司第五十四研究所，石家莊 050081；2.天津市海河管理中心，天津 300231；3.河北工業大學電子信息工程學院，天津 300401)

多旋翼飛行器又稱無人機，其構造簡單緊湊、行動十分靈巧、運動格外穩定[1]，在軍事領域與民用領域均展露出很大的應用價值，四旋翼機已廣泛應用于航空攝影、遙感測量、實時監測、軍事偵察、農藥噴灑等行業[2-4]。但是其同樣擁有續航時間短、載重量低等問題，在配送東西過程中難免會遇到懸掛的東西掉落的問題，造成無人機的不平衡，如何讓無人機在懸掛質量突然增加或者減少的情況下能夠快速恢復平衡是一大難點。

如今，隨著無人機的研究逐漸深入，中外的諸多科研機構和大學都對四旋翼無人機進行了很深入的研究。目前相關專家提出了很多四旋翼無人機的控制方法，其中最經典的就是比例積分微分(proportion integration differentiation，PID)控制[5]。PID控制有著原理簡單、控制技術成熟、易于實現的優點。Ji等[6]提出了傾斜四旋翼機的新概念，獨立控制無人機的旋轉與平移，建立了一個完整的動力學模型，其中考慮了參數不確定性和外部干擾，提出了一種自適應快速有限時間控制方法，最后通過對比仿真實驗驗證了控制器的有效性和魯棒性。Zhang等[7]提出了一種預測滑膜控制方法，并將其應用于飛行器的運動控制中。實現了在干擾環境下的跨域過渡，最后通過與PID控制器的對比仿真，驗證了控制方案的可行性與魯棒性。Cervantes-Rojas等[8]開發了一種自適應控制器來解決四旋翼機的軌跡跟蹤問題，提出了利用神經網絡與模糊推理系統進行交互作用的模式。在室外環境進行實驗，證明了基于動態域名服務(dynamic domain name server，DNNs)和高木-關野(Takagi-Sugeno，T-S)技術相結合的算法相對于經典的控制器具有更好的性能。南京航空航天大學從1958年開始才進行無人機方面的研究。王源等[9]提出直接坐標法控制無人機的飛行軌跡，實現四旋翼無人機自主導航控制，有效地保證系統穩定性和響應的快速性。2015年北京航空航天大學提出了一套基于自抗擾控制的姿態解算法[10]，該算法很好地解決了無人機系統狀態耦合性高和建模產生的狀態誤差問題，所設計的自抗擾控制系統在快速響應、無超調的前提下，具有很強的抗干擾能力以及較高的控制效率。2018年，王春陽等[11]提出了一種基于線性自抗擾的軌跡跟蹤控制系統設計方案，可以很好地克服無人機的強耦合性、模型不確定性以及外部干擾問題，滿足無人機姿態調節快速和高穩定度的控制要求。

在充分了解無人機的結果和飛行原理的前提下，現利用最簡單也最經典的PID控制，調整PID參數，使無人機在懸掛質量突然改變的情況下快速恢復平衡，持續穩定飛行，在Simulink上搭建系統模型，得到仿真結果，證明飛行器可以得到穩定有效的控制，提高飛行器的性能。

1 數學模型建立

1.1 坐標系的轉換

四旋翼無人機在空間飛行時，為了方便地描述無人機的轉動方程，建立了四旋翼飛行器的機體坐標系，它的坐標原點是飛行器的中心，xy水平面即是4個旋翼所在的水平面，z軸垂直于xy水平面。此種坐標系建立在飛行器本身上最為方便,可以用B表示。地面坐標系是建立在假設地面為水平面的基礎上，一般用E表示。

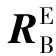
(1)

(2)

(3)

(4)

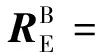
(5)

式中：θ、ψ、φ為歐拉角，用來描述E系到B系轉換需要的角度；θ為俯仰角，表示無人機與水平面之間形成的夾角；ψ為偏航角，表示無人機在地面的投影和地軸之間的夾角；φ為滾轉角，表示無人機繞中心對稱軸旋轉過的角度。

1.2 動力學數學模型

無人機的數學模型可以分為線性運動的數學模型和角運動的數學模型，線性運動的數學模型可以根據經典力學的理論來描述。由于無人機各項參數十分復雜，在最后對控制效果影響較小的前提下，做以下假設。

(1)將四旋翼飛行器視為剛體，在飛行器的聚合中心有著均勻的紋理和質量中心分布。

(2)忽略飛行器的四個旋翼與其相應電機之間的摩擦以及四旋翼飛行器中的空氣摩擦。

(3)由于四旋翼飛行器的飛行高度不是很高，因此受到地球重力的影響也非常小，所以認為它受到的重力在飛行過程中受到的重力不變，即重力加速度不會改變。

(4)假設由旋翼旋轉而產生的升力垂直于相應的旋翼，則該升力的大小與旋翼的轉速的平方呈線性關系。

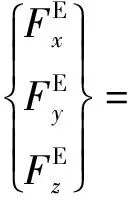
四旋翼飛行器飛行過程中飛行過程中主要受到3個力的影響，這3個力是旋翼產生的拉力，飛行過程中的阻力和來自地面的重力[12]。可得四旋翼飛行器在地面坐標系中的受力表達式[式(6)]，四旋翼飛行器的線性運動數學模型表達式[式(7)]。

(6)

(7)

(8)

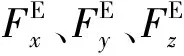
(9)

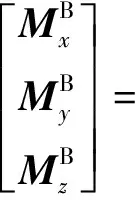
(10)

式中：L為電機軸中心到無人機質心之間的距離；Jr為旋翼的轉動變量；c為空氣阻力系數；p、r、q為機體沿三軸方向的角速度分量；d為反扭矩系數，且Ω=Ω1+Ω2-Ω3-Ω4。

因為四旋翼飛行器的結構對稱，所以機體整體轉動慣量可以用式(10)表示，即

(11)

式(11)中：I為剛體對定軸的轉動變量；Ixx、Iyy、Izz為3個方向上的轉動慣量。

將式(10)與式(11)綜合便可以得到四旋翼飛行器在機體坐標系中的角運動表達式，如式(12)所示。

(12)

2 PID控制方法

2.1 PID結構

姿態控制算法主要是采用串級PID控制[13]，這種控制系統不僅原理簡單、魯棒性強，而且通用性高。四旋翼飛行器運動過程中需要控制的量包括3個位置量：x、y、z和3個姿態控制量：θ、φ、ψ。單個閉環PID控制器[14]很容易減慢系統處理速度。由于姿態角的變化與位置坐標的變化之間存在因果關系，因此控制系統采用順序控制進行雙重設計閉環PID控制。內環是用于調整無人機姿態角變化的姿態控制環，外環是用于控制無人機位置坐標變化的位置控制環。這種串級控制方法往往都會取得不錯的效果。

PID的結構圖如圖1所示，PID的輸入信號為e(t)，輸出信號為u(t)。它主要可以分為比例、微分和積分三部分，比例是PID控制器的基礎部分，一切都是圍繞比例部分作用的。積分部分是為了消除因比例部分帶來的穩態誤差，而微分部分則是抑制積分帶來的超調作用。這三部分的不同組合將會帶來不同的作用，因此調整3個控制系數對于PID控制來說十分重要。

圖1 PID結構

e(t)=i(t)-r(t)

(13)

(14)

式中：i(t)為PID輸入的信號；r(t)為系統實際輸出的信號；Kp為比例系數；Ti為積分時間常數；Td為微分時間常數。

參數整定是PID控制器的核心，也是其最難的部分，直接在控制系統中通過不斷的試驗去調整參數，這種方式簡單不需要很復雜的數學計算，并且調試成功后更加貼近實際應用，但缺點就是太過耗費時間并且對試驗人員的經驗要求很高。實驗調整PID的參數步驟如下。

(1)合理確定一個采樣周期，確保系統能夠穩定運行。

(2)調整系數的大小直到系統將要出現振蕩現象，與此同時，仔細觀察記錄比例系數和臨界振蕩周期。

(3)利用數學公式解算出PID控制器參數。

2.2 數字模型的簡化

為了方便四旋翼飛行器的控制器設計，需要考慮到實際情況增加約束條件，進而使數學模型在合理的范圍內得到最大程度的簡化。當小型四旋翼飛行器在室內慢速飛行時，由于沒有風力的干擾，且轉動速度十分緩慢，所以能夠添加以下約束條件。

(1)忽略空氣阻力因素帶來的干擾，即把空氣阻力矩和空氣阻力的大小看作0。

(2)因為實驗用的是小型四旋翼飛行器，其4個螺旋槳無論是質量還是尺寸都十分小，因此忽略陀螺效應力矩，即Jr為0。

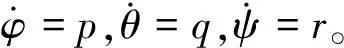
為了方便描述，令

(15)

當在無風條件下或者是只對無人機產生小角度干擾的環境下，低速穩定飛行或到達懸停狀態時進行無人機實驗，由于無人機的飛行姿態角度變化很小，所以空氣阻力因素和陀螺效應都可以暫時忽略，故可以在上面的基礎上進一步簡化無人機的數學模型，從而達到如式(16)、式(17)所示的最簡模型。

(16)

(17)

2.2 外環位置控制算法

位置控制環可通過PID計算獲得運動方向上的3個預期加速度，例如預期位移與實際位移之間的差，各方向的計算公式為

(18)

式(18)中：kPi、kIi、kDi(i=x,y,z)分別為比例系數、積分系數和微分系數；xd、yd、zd為3個方向上的預期位移；x、y、z為實際位移。

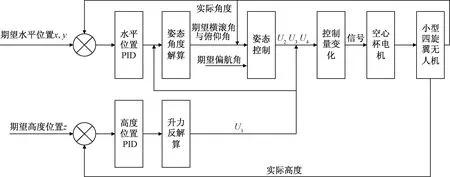
圖2 位置控制流程圖

由式(19)可得U1，再輸入期望偏航角得出期望的滾轉角和期望的俯仰角為

U1=

(19)

(20)

式(20)中：下角標e表示該物理量的期望值。

2.4 內環姿態控制算法

在內環姿態控制也是串級結構，首先將外環送來的期望姿態和實際反饋回來的值輸入給角度控制器，角速度控制器根據期望角速度與實際角速度算出U2、U3和U4的值，最后將其變換為電機的期望拉力解算出各旋翼的期望轉速公式為

(22)

式中：kPi、kIi、kDi(i=2,3,4)分別為比例系數、積分系數和微分系數。

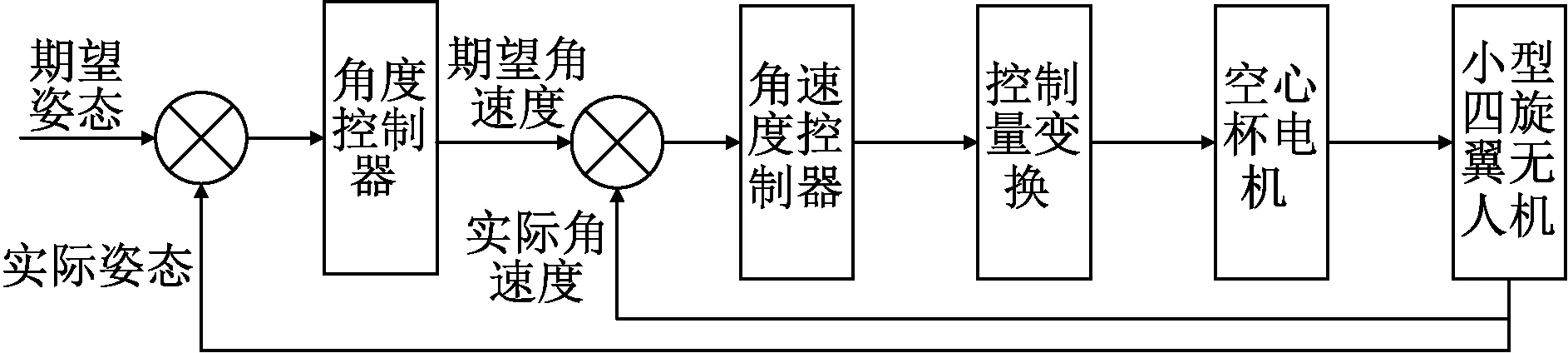
圖3 姿態控制流程圖

期望角速度的計算公式為

(23)

白煞留下和鐵衛連夜清理黑旗會分壇，因為與黑旗會博弈須要充裕的銀子作基礎，所以蕭飛羽臨走時吩咐將所有值錢的東西帶去安和莊，余下的事情交給樊虎帶領的伙計。白煞和鐵衛搜索發現天問大師和紫陽道長要找的少林俗家弟子之首的白云飛竟然囚禁在地牢里。

經過多次試驗，最終得到這些PID控制系數如表1所示。

表1 PID參數

2.5 Simulink仿真結果分析

利用上述求出來的PID參數進行模型的構建，在Simulink中進行仿真，得到的外環位置仿真結果如圖4所示，其中黑色曲線為x軸的期望位置與實際位置，紅色曲線為y軸的期望位置與實際位置，綠色曲線是z軸的期望位置與實際位置。

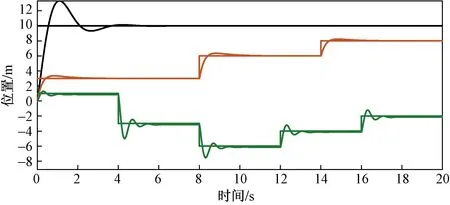
圖4 位置仿真結果

仿真模型中預期坐標為x=10，y=3、6、8，z=1、-3、-6、-4、-2，由仿真曲線可知，x點在4 s內實現了無人機從初始坐標到預期坐標的平滑過渡，穩態誤差在±4范圍內；y點在1 s內實現無人機從原來坐標到預期坐標的平滑過渡，穩態誤差在±1范圍內，超調量較小，很快進入穩定狀態；z點在1.4 s后趨于平穩，高度波動較大，但響應速度快。整體來說，系統可以取得較好的控制效果，使系統迅速穩定下來。

在Simulink中進行仿真得到姿態控制效果，其中俯仰角、滾轉角、航偏角的變化分別如圖5所示。

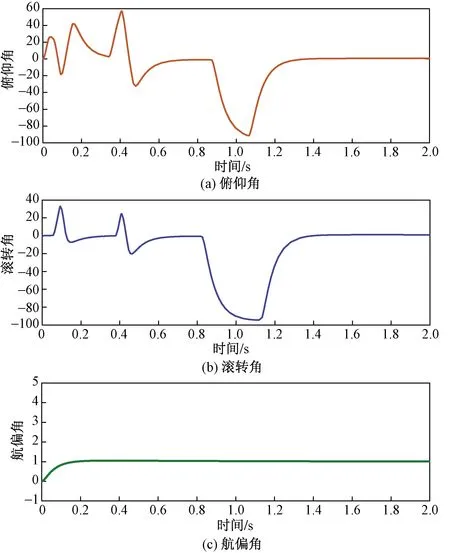
圖5 俯仰角、滾轉角和航偏角曲線圖

圖5(a)和圖5(b)中，俯仰角和滾轉角在曲線波動后基本穩定在期望值零點，其曲線波動較大，最大達到60，最小將近-100，但是控制系統的穩定性較好，基本可以在1.5 s內近似恢復期望值0。圖5(c)中，無人機偏航角賦值為1,，使無人機方向不發生變化，無人機在0.2 s內進入固定偏航角狀態，能夠維持穩定。由此可以看出系統調整速度很快，穩定性良好，取得了較好的控制效果。

3 滑膜控制器的設計

3.1 控制器設計

控制器所要達到的目標是使四旋翼無人機能夠在一個固定的高度進行相對懸停，并以指數趨近律為核心來設計滑膜動態控制器[15]。通過公式推導將3個歐拉角θ、ψ、φ解耦，分別對其進行控制以實現整體飛行控制，以下是推導過程

通過反饋線性化，得到的線性系統公式為

(24)

(25)

(26)

(27)

為了方便后續推導，令

(28)

已知s=Cηi，對其求一階導數，可得

(29)

式(29)中：C為常系數，ε>0,k>0,i=1,2,3；-ks為指數趨近項；-εsgn(s)為等速趨近項。

將式(24)代入式(29)中，得到式(30)，即

ui=(CiBi)-1(-CiAiηi)+s

(30)

式(30)中：Ci=[15 1],Bi=[0bi]T,ε=10，k=3.5，i=1,2,3，ηi=[1 1]T,利用趨近律對四旋翼飛行器的高度z實時控制和反饋。則狀態方程為

(31)

式(31)中：f1=[0-g]T，g為重力加速度。

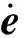
(32)

設切換函數為

(33)

由高度誤差變化率可得

(34)

將式(31)和式(33)代入式(29)中，可得式(35)，其中c=30,ε=10,k=3。

(35)

3.2 仿真結果分析

圖6是高度z的變化曲線，在圖6中可以看到，高度z的曲線在1.5 s內達到穩定，并且沒有超調。由此可知設計的滑模控制器可以使四旋翼無人機在一個固定的高度進行相對懸停，圖6懸停在5 m處，滑膜控制器可以實現對無人機的控制。

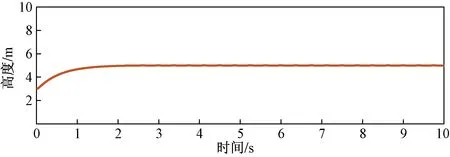
圖6 高度z的變化曲線

4 結論

分析了無人機的運動原理，建立了完備的數學模型。在數學模型的基礎上做了一個仿真驗證，實現了無人機的期望飛行。驗證了數學模型的正確性。得到的主要結論如下。

(1)在基本限制條件下進行受力分析，進一步得到了無人機運動的線性運動模型以及角運動模型，最后根據實驗條件再進行模型的簡化，有利于后期的模型計算。

(2)在Simulink中搭建出仿真模型，經過多次嘗試得到的PID控制系統參數可以有效地區控制系統的穩定性，取得較好的控制效果。

(3)設計滑膜控制器，并在Simulink中搭建出相應的仿真模型，可以實現期望的效果，使四旋翼無人機能夠在一個固定的高度進行相對懸停。