線性系統的系統辨識綜述

李 昱，袁 磊

(1.北京理工大學機電學院，北京 100081；2.北京特種車輛研究所，北京 100072)

0 引言

系統辨識是使用傳遞函數對所研究系統進行表征。在研究系統特性的過程中，掌握如何正確使用系統辨識工具十分重要。

目前對線性系統辨識的研究已經頗為深入。20世紀50年代末期便出現了傳統的系統辨識，傳統的系統辨識存在一定的局限性，僅適用于線性系統，對非線性系統的估計準確性較差[1]。近年來伴隨著計算機硬件以及神經網絡、遺傳算法等理論的發展，系統辨識理論在非線性系統中又迎來了新的分析方法，這些方法統稱為新型系統辨識方法[2-3]。

針對系統辨識參數計算算法的綜述文章較多，但是針對在辨識過程中的系統模型結構建立以及選取的文章較少；同時，在建模過程中，模型結構正確地建立與合適地選取對計算的效率與最后結果的精度都有重要的影響[4-5]。本文著重對在線性系統辨識過程中的常用結構模型的形式、適用場景以及使用方法進行介紹與分析，同時介紹了適用于常用模型的計算算法，并使用系統辨識方法對實際問題進行了分析與求解。

1 系統辨識的概念及要素

系統辨識中“辨識”的定義[6]是1962年由美國著名控制理論專家Lotfi Aliasker Zadeh教授提出的：“辨識就是在輸入和輸出數據的基礎上，從一組給定的模型類中，確定一個與所測系統等價的模型。”

線性系統指的是同時滿足疊加性與均勻性的系統，線性系統可用微分或者差分方程來表示。一般而言，線性系統的系統特性比較簡單，處理起來較為容易，目前對線性系統辨識的研究較多，方法較為成熟。相對而言，非線性系統整體看來更加復雜，其中局部可以簡化為線性系統處理。對非線性系統的辨識往往是將傳統算法與神經網絡、模糊邏輯、遺傳算法等相結合[7]，目前研究還處在發展的階段。

系統辨識理論是現代控制理論的一個重要分支，系統辨識起源于現代控制理論的發展。在現代控制理論中，對于系統的設計和配置等都是在對系統動態特性掌握的前提下進行的，對系統動態特性的研究中，純理論計算在現實條件下十分復雜甚至不可行，這時便需要利用實驗數據直接擬合出特性相同或者相似的系統，從而代替原始系統，這種方法被稱作系統辨識[8]。

理想條件下，一些相對簡單的線性系統可以直接由物理學關系推導得出，例如在無誤差以及環境干擾情況下的理想彈簧阻尼系統，任意兩點間的速度、加速度等物理學關系可以由運動學方程組推導而出[9]。但現實條件下系統通常涉及到多個組成部分，每個部分之間的配合無法做到完全理想化，并且存在外界擾動，實際的傳遞關系更加復雜，物理學先驗知識一般只能作為補充，利用系統辨識以及相關算法才可以得到更準確的數學表達式[10]。

系統辨識包含三個重要的因素：實驗得到的系統輸入輸出作為辨識的數據基礎；采用的適當的系統結構模型以最大化擬合的準確度；使用的參數計算算法以獲得系統模型中的待定系數[11]。理想化的簡單系統可以使用白箱法或直接計算法進行直接辨識，該方法是使用物理公式直接推導得出系統的傳遞函數；真實條件下的復雜系統可以使用黑箱法進行辨識，在只關注系統的輸入輸出而不關注系統的內部聯系下找到等價系統的傳遞函數；將兩種方法結合可以根據白箱法的系統特點得到關鍵參數(例如系統階次等)為黑箱法的模型構建提供依據，稱作灰箱法。在涉及到黑箱法的辨識中，最重要的兩個步驟是辨識系統模型結構的選取與模型中參數的計算[12-13]。

2 模型結構與計算算法

2.1 線性系統建模的模型結構

2.1.1線性非參數化模型

線性非參數化模型，亦或直接辨識估計法，分為沖擊響應直接辨識以及頻率響應直接辨識，適用于簡單系統在受到脈沖輸入的實驗條件下在時域與頻域進行的系統辨識。

在時域下，一個線性系統可以用脈沖響應來描述[14]。該系統的性質為：

(1)

式(1)中，脈沖響應系數gk是使用相關分析法直接從輸入/輸出數據中估計得出的[15]。

線性系統的頻率響應是其脈沖響應的傅里葉變換。輸入和輸出之間的關系為：

y(t)=G(z)u(t)+v(t)

(2)

系統的頻率響應可以使用頻譜分析法直接估計[16]。

線性非參數化模型結構簡單，模型中沒有需要調試的參數，計算量小，適用于一些簡單的線性系統在受到脈沖輸入時的系統辨識。在文獻[17]中，對沖擊響應下的磁懸浮軸承進行仿真辨識，將軸承與轉子分別進行了簡化，并在低轉速下將系統中各部分視作剛體建模，最后得出準確的辨識結果。文獻[18]對軸承在不同類型的沖擊響應下進行系統辨識，建立系統模型并著重使用改進的相關分析算法對參數進行估計，并驗證了該算法的可行性。因此在研究軸承一類簡單的系統受到沖擊響應下的系統特性，使用直接辨識估計法可以得到理想的結果。

2.1.2線性參數化模型

線性參數化模型的適用范圍廣泛，模型種類較多且較為復雜，依據不同的實際情況，前人設計出了多種模型結構，每種結構適用于不同特性的系統。

比較常見的線性參數化模型有：輸入輸出模型(傳遞函數模型)、狀態空間模型、過程數學模型和多項式模型[19]。

1)傳遞函數模型

傳遞函數模型以傳遞函數的形式對系統進行表示，形式為：

(3)

該模型適用于連續時間與離散時間系統。由式(3)可知，系統的輸入輸出傳遞關系完全由Num/Den決定，因此，根據極點與零點的個數以及各項系數便可確定系統的傳遞函數。系統階次可以通過系統的結構配合、物理學先驗知識進行初步確定，對于參數的估計可以使用工具變量法(instrumental variable method，IV)[20]、狀態變量濾波器法(state variable filter method，SVF)、廣義泊松矩函數法(generalized poisson moment method，GPMF)以及子空間狀態估計法(subspace state estimation method,N4SID)[21]進行。

在線性參數化模型中，傳遞函數模型的結構較為簡單，在該模型中，需要調試的參數有零點以及極點的個數，對于一些簡單或者理想化的系統，使用傳遞函數模型更加快捷方便。文獻[22]對冰箱的內部溫度的動態平衡狀態進行研究，利用傳遞函數模型對其進行建模，集成和發展了冰箱負荷計算的傳遞函數模型,簡化了計算過程。文獻[23]對人體脈搏系統進行研究，將脈搏信號看作是一線性時不變系統在準周期脈沖序列激勵下的輸出，并建立了到脈搏系統的傳遞函數。仿真結果表明，該模型可以較真實地模擬人體脈搏信號。在簡單的單輸入單輸出系統的辨識中，使用傳遞函數模型進行數學建模的準確度較高。

2)狀態空間模型

狀態空間模型以狀態空間表達式[24]的形式對系統進行表示，形式如下：

(4)

和傳遞模型一樣，該模型也適用于連續時間與離散時間系統。對于狀態空間模型而言，最重要的參數是模型階次，也就是狀態向量x的維數。同樣，系統的階次可由先驗知識進行初步確定[25]，對于狀態空間模型，參數矩陣的估計常用N4SID(子空間狀態估計法)和PEM(最小誤差估計法)來計算[26]。

狀態空間模型在建模的過程中引入了對多個信號的矩陣表示，維數上更高，對于多輸入多輸出的系統而言，可以更好地進行表示。文獻[27]在對汽車懸架系統特性的研究中，分別選取車身多個部位進行測量，利用狀態空間模型對該系統進行建模，建立了4個輸入3個輸出模型，通過建模及仿真，得到了可以有效地研究汽車振動特性的方法。文獻[28]研究了雙率系統的系統辨識，經過推導得出該系統可被視作線性時不變多變量系統，研究該系統時搭建了狀態空間模型，并證明了其可靠性。在研究多變量系統時，系統每個輸入對應于每個輸出均存在一個傳遞關系，使用狀態空間模型可以使用矩陣的形式對系統的輸入輸出以及系統特性進行更有效地表示。

3)過程數學模型

過程數學模型用增量K、延遲Td和一個或多個時間常量來描述一個系統，形式如下：

(5)

式(5)中，e-sTd為系統延遲項，1+Tns為系統零點項，該模型是傳遞函數模型的簡化。在工業過程中，針對典型的控制系統，使用過程數學模型表征系統特性準確度較高。

4)多項式模型

多項式模型以多項式的形式對系統進行表示，其中包括四個子模型：①自回歸各態歷經模型(autoregressive exogenous,ARX models)；②有外源變量的隨機預測數學模型(ARMAX models)；③輸出誤差模型(output-error models)；④時間序列預測模型(box-jenkins models)。

四種子模型均是多項式的形式，差別在于參數部分的表示有所不同，與傳遞函數模型以及狀態空間模型不同的是其只適用于離散時間系統。

對于ARX模型來說，該模型是Matlab系統參數辨識中最經常使用到的參數模型，常用的模型結構為：

(6)

該模型需要調試的參數為極點個數、零點個數，以及系統的純延時大小，對于沒有時延的系統，可以將延時參數設置為1。模型參數可使用ARX以及IV算法進行估計。ARMAX、OE和BJ模型則是在ARX模型的基礎上，引入了擾動而來的。

ARMAX模型的基本結構為：

(7)

OE模型的基本結構為：

(8)

BJ模型的基本結構為：

(9)

對于ARMAX、OE和BJ模型，參數的估計通常使用誤差估計方法。上述四個子模型是多項式模型的四種不同的表述形式，其基本結構為：

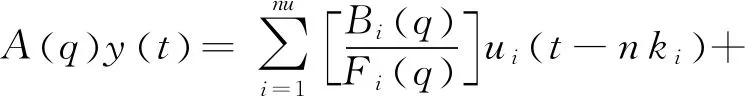
(10)

多項式模型的優點：其一可以通過逐步疊加高次項來進行逼近，且往往項數越高，結果越貼近原始模型；其二，通過選擇不同的復雜度子模型，既可以對簡單系統進行表達又可以對復雜系統準確表征。文獻[29]對阻尼器進行動力學建模，該阻尼器擁有多個組件并以不同方式相連，在建模時使用到了多項式模型，并在仿真后進行了模型驗證以及誤差分析，建立了一個12階多項式參數模型；同樣在文獻[30]中，對磁流變阻尼器進行了研究，認為高次多項式擬合容易導致擬合曲線的兩端出現劇烈地振蕩，并且最后使用了分段三次多項式來表征系統并消除了振蕩；在文獻[31]中使用多項式模型對傳感器的動態特性進行了建模并完成系統辨識；文獻[32]在進行BDI指數預測時使用了ARMA以及ARMAX模型；文獻[33]在進行徑流短期預測中使用了ARMAX模型；文獻[34]同樣使用ARMAX模型對穩壓設備進行建模。

對于以上各模型來說，不同的模型結構在傳遞函數的表達方式上存在差異，其本質都是為了用數學公式的形式表示出系統特性。例如傳遞函數模型與狀態空間模型可以相互轉化，過程數學模型則是對傳遞函數模型進行簡化而來，而多項式模型中的四個子模型均是對基本結構進行不同程度地簡化。其根本目的都是為了表達出系統的傳遞關系，不同點在于多項式模型等相對復雜的模型結構對于復雜的系統表征更加準確，相對來說系統擬合度更高，但計算量也相應增大。因此，根據不同實際情況選擇合適的系統模型十分關鍵。

通過對上述各模型結構的理論分析以及學者們在系統辨識實驗中的經驗匯總，表1對線性系統辨識的模型結構相關特性做出歸納。

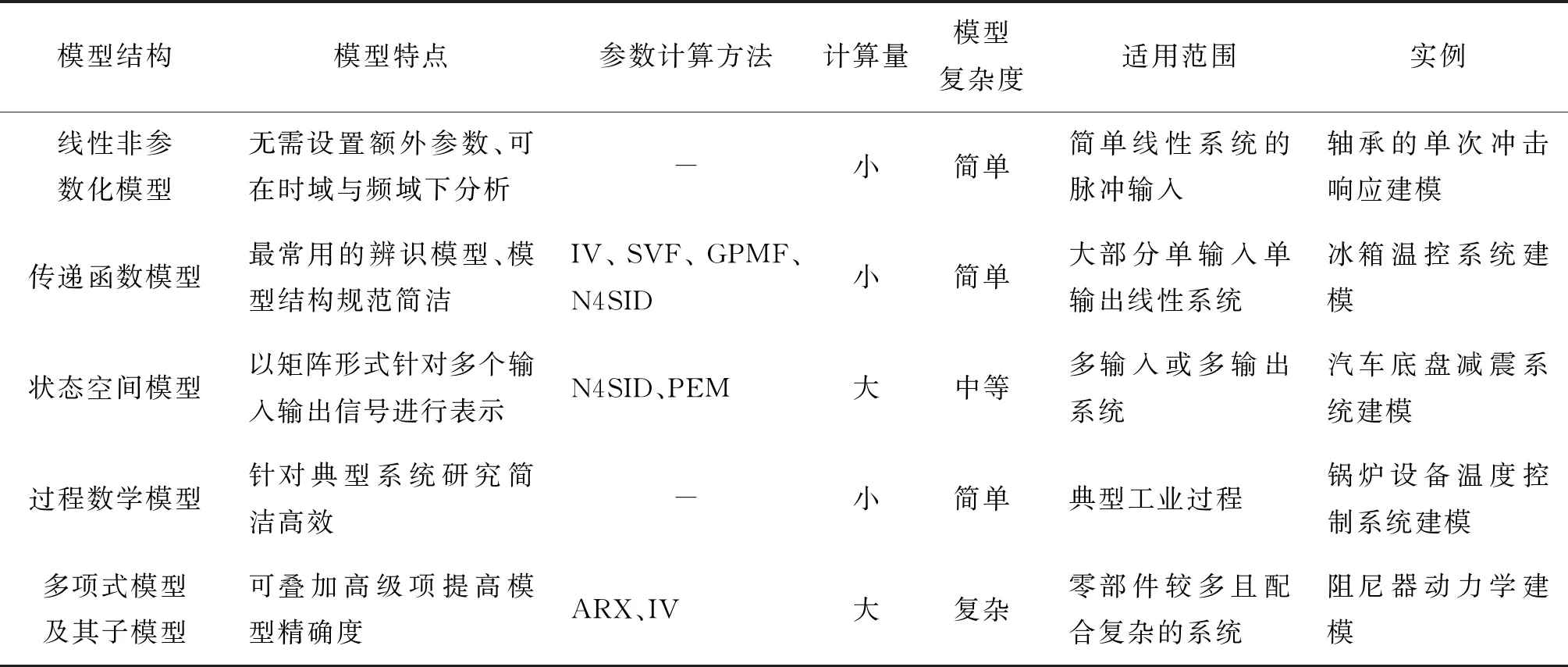
表1 常用傳遞函數模型結構特點Tab.1 Characteristics of commonly used transfer function model structures

2.2 模型參數的計算算法

線性系統常用的傳統參數估計算法經過多年的發展研究已經頗為深入，這里只簡單介紹一下上述涉及到的幾種算法[35]。

2.2.1工具變量法(instrument variable)

工具變量法，亦或輔助變量法(auxiliary variable)是一種最小二乘參數估計法的延伸，其定義如下：

(11)

在收斂不到真值θ的情形下，可以用一個輔助向量z(t)，使在N→∞時，輔助變量趨于(即收斂于)真值θ0。輔助變量法的關鍵在于如何構造一個滿足上述條件的輔助變量，也就是說輔助變量應當與噪聲v(t)不相關，而與φ(t)強相關。因此常見的一種選擇是由輸入激勵和一個確定性系統產生的輸出組成[36]。工具變量法與最小二乘法一樣，作為最普適的估計算法，在系統模型的參數估計過程中有著頻繁的應用。

2.2.2預測誤差法(prediction error estimate)

PEM采用數值優化方法來最小化代價函數VN(G,H)，定義如下：

(12)

式(12)中，e(t)為模型的測量輸出與預測輸出之差，e(t)為向量；代價函數VN(G,H)為標量值，下標N表示代價函數是數據樣本個數的函數，N越大，代價函數越精確。預測誤差法在狀態空間模型以及多項式模型的參數估計中應用頻繁。

2.2.3子空間辨識法(N4SID)

子空間辨識法可應用于多輸入多輸出模型，對于給定的一個未知的單入單出或多入多出系統，假定輸入測量值為u，輸出測量值為y，在系統可能存在噪聲的情況下，估計出系統的狀態空間模型。其直接利用輸入輸出數據的行與列估計出廣義觀測矩陣以及卡爾曼狀態序列，利用最小二乘法求出系統的狀態空間表達式[37]。子空間估計法對多輸入多輸出模型的估計效果較好，例如在狀態空間模型中的應用十分廣泛。

3 實際應用中不同線性系統辨識方法對比

在實際應用中，通過已知系統的特性、復雜度等情況可以先排除一些不適用或計算精度不高的方法。例如在簡單的兩物體鋼性接觸條件下可以首先使用傳遞函數模型，而在復雜的多物體系統中，可以首先使用多項式模型，在多輸入多輸出系統中，狀態空間模型則更適用[38-39]。

為了驗證并對比不同方法在實際應用中的區別以及適用性，本文對實際問題進行了實驗與仿真分析。實驗內容如下：已知某型炮彈及引信是通過螺紋剛性連接，獲得了炮彈在彈底受到的軸向沖擊與引信部位產生的軸向響應的相關數據，對炮彈底部到引信部位的響應傳遞進行系統辨識，以求得其彈底到引信的傳遞函數。

仿真部分使用的軟件為Matlab 2019b，本文調用了Matlab 2019b中內置系統辨識工具箱，其中上述算法的相關函數已整合為庫函數供用戶直接調用，并且可以選擇性使用內置的UI程序進行交互。由于計算量不高，分別使用了多種辨識方法進行計算，并對結果進行對比[40-42]。

已有數據是在1×10-5s的采樣間隔下，記錄的1 204組輸入輸出數據。使用Matlab 2019b軟件對收集的數據進行處理與分析，根據數據點繪制的時間-響應圖像如圖1所示。

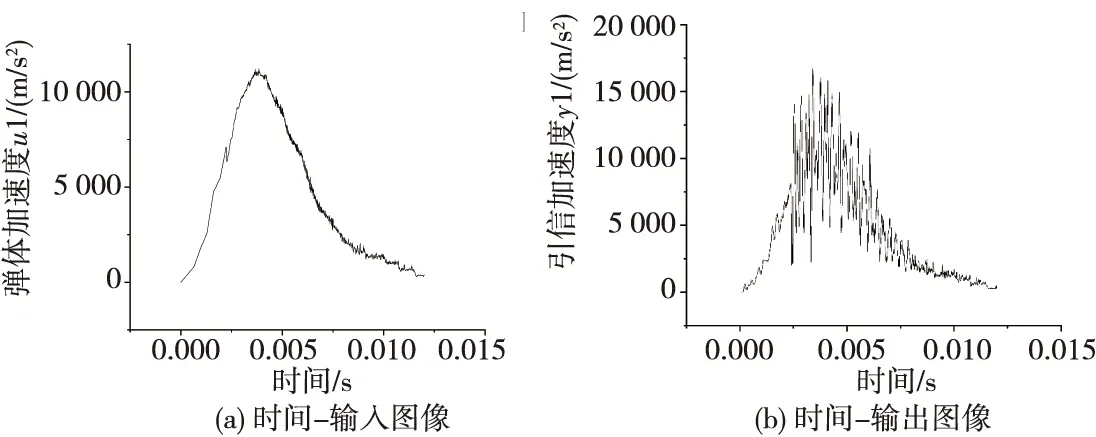
圖1 時間-響應圖像Fig.1 Time-response graph

仿真結果中，u1為彈體受到的沖擊加速度，y1為引信體受到的沖擊加速度。在引信彈體系統中，引信各部分以及彈體各部分間使用螺紋連接，系統的輸入振動以波的形式通過彈體結構以及螺紋傳遞給引信結構，實驗中將該系統視為線性系統，將輸入輸出數據導入Matlab進行系統辨識。鑒于對傳感器固定方式及引信內部結構沒有了解，遂使用黑箱法，即在不考慮物理學先驗知識的前提下進行辨識。由于系統的輸入為振動信號，因此選擇使用線性參數化辨識模型作為系統的模型結構，即將收集到的傳感器數據經過預處理后分別使用傳遞函數模型、狀態空間模型、過程數學模型以及多項式模型進行系統辨識，通過對模型中的自定義參數進行設置來得到不同擬合度的曲線，然后選擇性地在圖像中展示了幾種不同擬合度的結果，圖中標有數字序號的代表仿真計算出的響應曲線。實驗中將70%的擬合度定為可接受的擬合度，在這個數值附近或大于這個數值，則認為傳遞函數表達式可以較為準確地表征原始系統。為方便觀察辨識曲線的差異，對不同辨識方法的結果曲線均取前30%進行放大與原曲線進行對比。

圖2為根據實驗輸入輸出數據點繪制的引信部位實際響應的加速度-時間圖像。下文使用不同系統辨識模型對彈體引信進行系統辨識，得到的擬合度數據為仿真結果相對實際響應的準確程度。

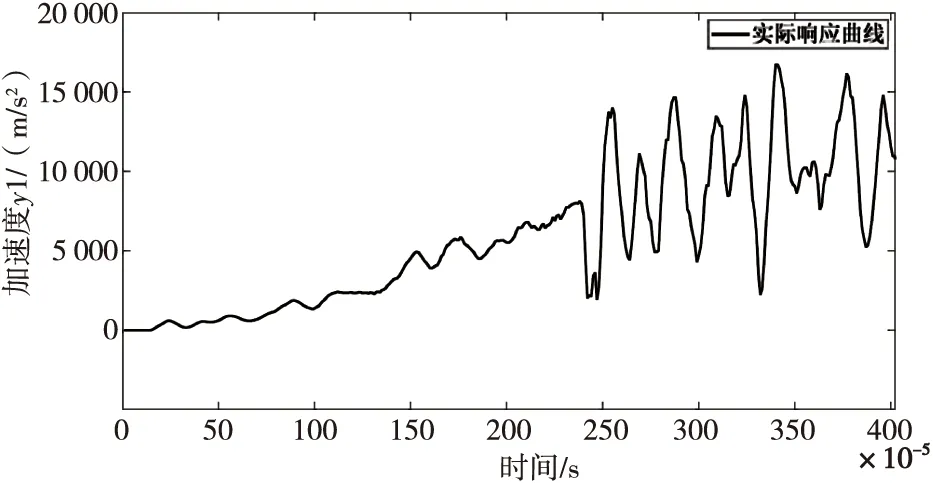
圖2 實際響應曲線Fig.2 Actual response curve

圖3為使用傳遞函數模型對系統進行建模的仿真結果。結果顯示仿真曲線與實際模型曲線有一定的差異，擬合度最高在72%左右，該表達式分母為五階，分子為三階，擬合度滿足要求且表達式簡潔，故使用傳遞函數模型表征系統較為合適。

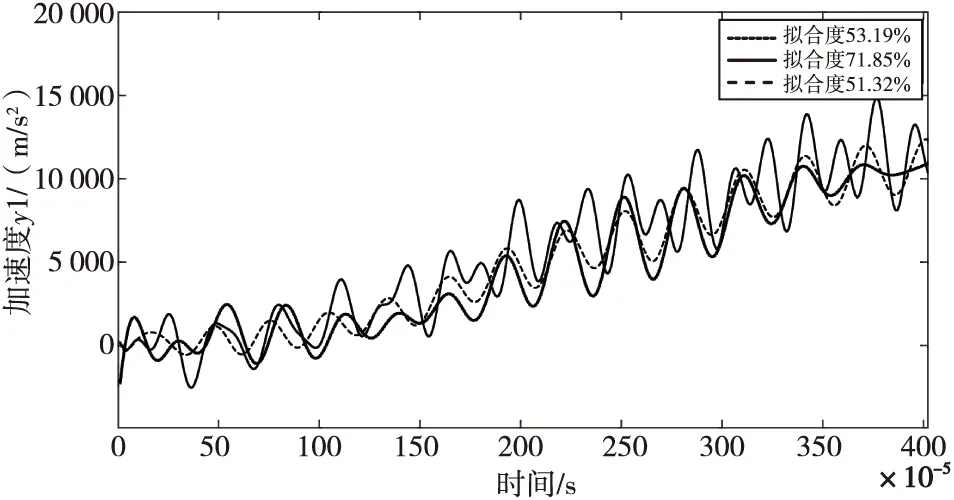
圖3 傳遞函數模型仿真結果Fig.3 Simulation results of transfer function model

圖4為使用狀態空間模型對系統進行建模的仿真結果，從辯識結果可以看出，實線仿真曲線與實際模型響應曲線差別較小，該曲線是在將模型階次設置在30次附近時所得，擬合度可以達到71%左右，該擬合度相對較高，但是30階模型得到的系數矩陣的規模達到了30×30，過于復雜，故適用性不高。

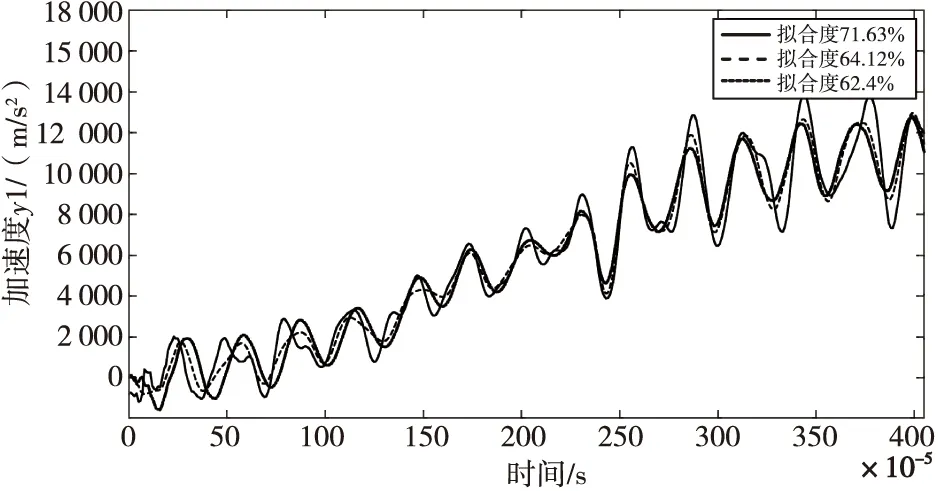
圖4 狀態空間模型仿真結果Fig.4 Simulation results of state space model

圖5為使用過程數學模型對系統進行建模的仿真結果。經過仿真，得到過程數學模型的最大擬合度在58%左右，雖然得出的傳遞函數表達式簡潔，但是曲線擬合度低于70%，故認為此模型不適用于該實驗。

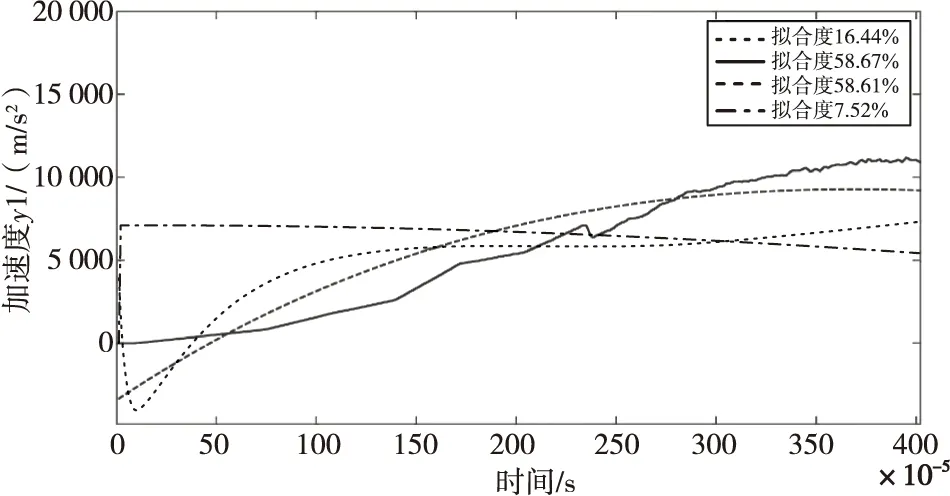
圖5 過程數學模型仿真結果 Fig.5 Simulation results of process model

圖6為使用多項式模型中的ARX子模型對系統進行建模的仿真結果。圖中四條曲線中有三條擬合度較高，其中實線擬合度超過了90%。由圖像可以得到結論：該系統在ARX模型建模下，隨著對極點零點數目配置的提高，其擬合度會逐漸上升，最終達到94%左右，此時擬合度完全滿足要求，但該傳遞函數多項式項數達到了300項以上，計算量龐大且表達式繁瑣，故不推薦采用此方法。

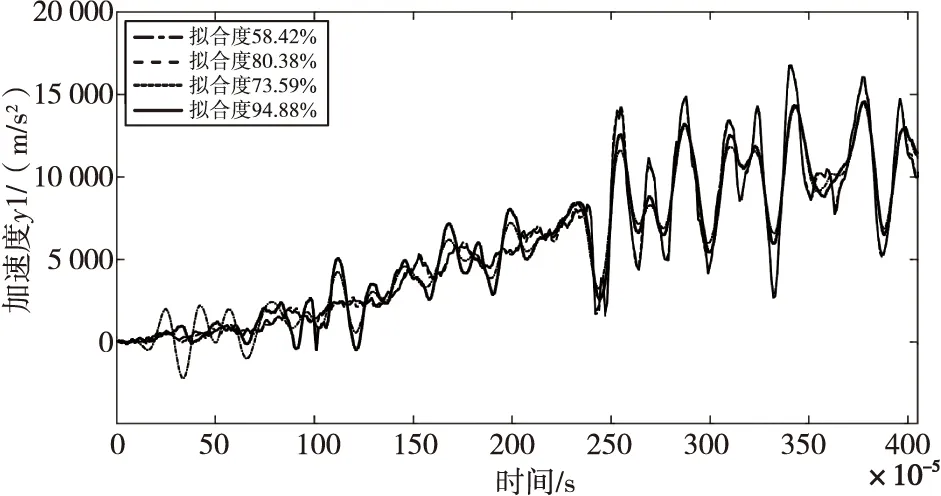
圖6 ARX模型仿真結果Fig.6 Simulation results of ARX model

圖7為使用多項式模型中的ARMAX子模型對系統進行建模的仿真結果。使用ARMAX模型仿真出的傳遞函數擬合度在70%左右，但在零點極點個數達到上百個時，計算速度明顯慢于ARX模型，故ARMAX模型同樣不適用于該系統。

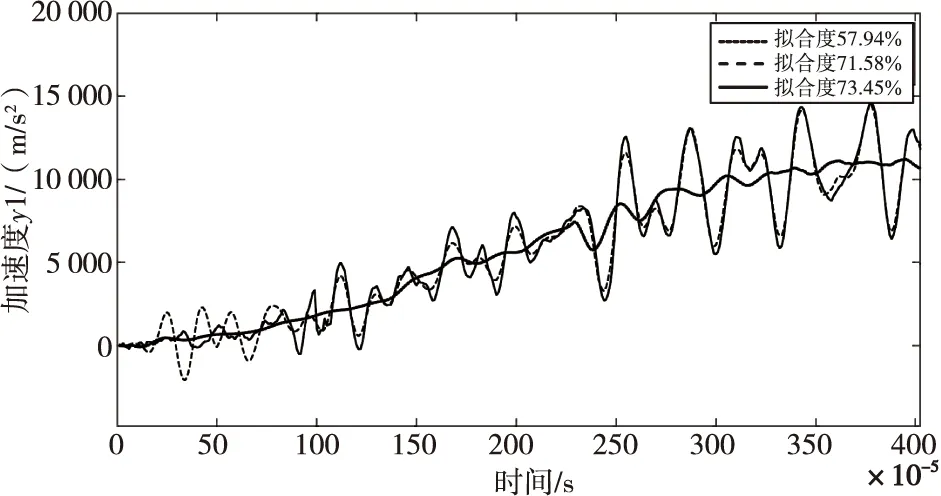
圖7 ARMAX模型仿真結果Fig.7 Simulation results of ARMAX model

圖8為使用多項式模型中的OE子模型對系統進行建模的結果，可以看到，當使用OE模型仿真時，模型階次設置為10次時，擬合度最高達到80%左右。傳遞函數的項數為11項，相對于之前的ARX以及ARMX模型在80%擬合度時，計算量最小；相對于傳遞函數模型擬合度更高，表達式也比較簡潔，因此OE模型對于炮彈引信振動響應系統的辨識來說也是一種適用的方法。

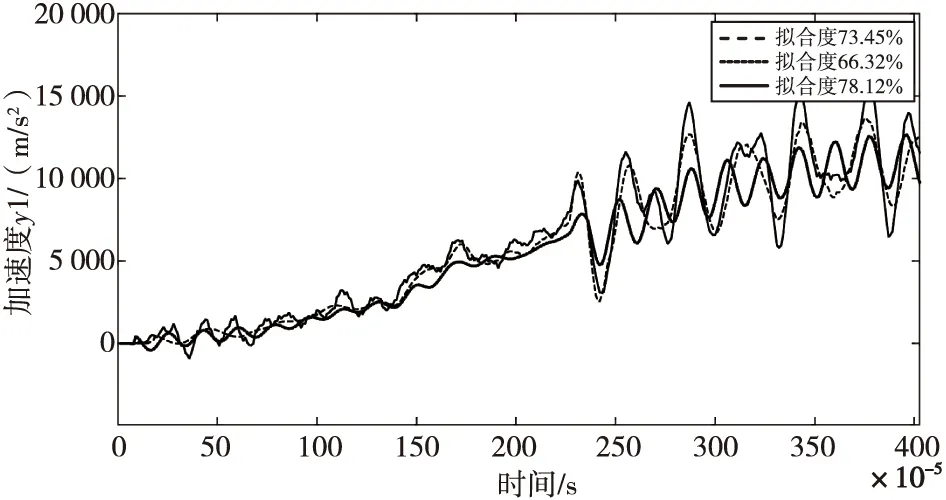
圖8 OE模型仿真結果Fig.8 Simulation results of OE model

圖9為使用多項式模型中的BJ子模型對系統進行建模的仿真結果。BJ模型在模型階數達到30上下時，擬合度可以達到80%左右，此時多項式項數在60項左右。模型簡潔程度要次于OE模型。綜上所述，本研究中不同模型的擬合度和表達式復雜度如表2所示。

表2 傳遞函數擬合度Tab.2 Transfer functions’ fitting degree

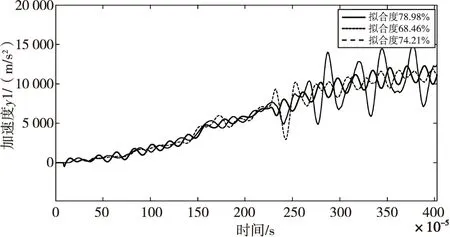
圖9 BJ模型仿真結果Fig.9 Simulation results of BJ model

從以上仿真結果可以看到，在彈體引信模型的系統辨識研究中，使用傳遞函數模型和OE模型獲取系統傳遞函數，可以做到在傳遞函數表達式簡潔的同時，達到相對較高的擬合度，故選該模型來計算系統傳遞函數比較合適。

4 結論

系統辨識作為系統特性研究中的重要手段，近幾年來發展迅速，特別是針對線性系統的辨識方法已經發展成熟。在辨識的過程中，需要根據不同實際情況對辨識方法進行選擇以便得到更好的擬合函數，系統模型的選擇和參數辨識算法的選擇在這個過程中至關重要，合適的模型算法可以更輕松地得到擬合度高的函數。

本文詳細介紹了線性系統的辨識模型，并歸納總結了不同模型的特點與適用范圍。在簡單系統受到脈沖輸入的實驗條件下(如瞬時沖擊)可首先使用線性非參數化模型；在簡單系統受到非脈沖輸入條件(如振動)可以首先使用傳遞函數模型；在多輸入多輸出系統的辨識中，可以使用狀態空間模型以及子空間辨識算法；在已知傳遞函數符合傳遞函數模型且模型中部分階次項系數已知時，可采用過程數學模型；在復雜系統階次較高或對系統結構已知不多時，建議首先嘗試多項式模型。最后，本文開展了基于實際應用的系統辨識算法研究，結果表明，研究炮彈引信系統或結構及特性相似的系統時，可以首先嘗試使用傳遞函數以及OE方法進行建模。