基于SNAP結構微腔的位移傳感特性研究
陳 劍 董永超 王 晗 孫鵬輝
廣東工業大學機電工程學院 廣東 廣州 510006
1 引言
回音壁模式光學微腔以其高質量因數和較小模式體積的優點,近年來在傳感領域引起了廣泛的研究[1,2],比如在生物傳感[3],溫度傳感[4],以及壓力和位移傳感[5-7],當特定波長的光進入微腔時,光通過全內反射在狹窄的環內傳播并在繞行一周后相互疊加增強,這樣就形成了回音壁模式。WGM微腔與光波導組成耦合系統可以高效激發內部回音壁模式,由產生諧振的光波構成微腔的諧振譜。其諧振譜特征由光纖尺寸、微腔結構和耦合條件決定,改變耦合位置可以改變諧振譜中各諧振模式的耦合狀態,表現為中心波長偏移、透過率和Q值得變化等,研究諧振譜的變化規律可以實現基于微腔耦合系統的位移傳感。2011年,英國阿斯頓大學M.Sumetsky首次提出了SNAP結構微腔的概念,并給出了其分析理論模型,相較于其他WGM微腔中光的全內反射,SNAP微腔中的光在角動量勢壘定義的兩個焦散點之間來回循環震蕩,這使得微腔的模式場分布在軸向上明顯增長[8-11]。
綜上,為了實現大量程、高靈敏度,的微腔傳感測量,本文首先計算SNAP腔的模式譜。該傳感原理如圖1所示。寬帶光源通過光纖錐耦合進入SNAP微腔,在腔體內激發出多個軸向模式,其透過譜表現為多個諧振峰,當SNAP微腔進行軸向移動時會改變諧振峰的Q值和諧振波長,進而實現微腔軸向位置傳感。

圖1 SNAP位移檢測原理
2 理論模型介紹
2.1 SNAP腔模式理論SNAP微腔的有效半徑變化可以看曲線,其近似輪廓可以用下面的公式來表示[10,11]:
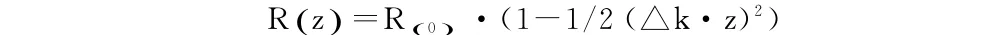
公式表明了諧振半徑R隨著諧振腔z方向坐標的變化情況,其中△k是諧振腔的曲率。最后,由q階厄米多項式和高斯函數可求得歸一化場強分布,表示如下:


2.2 snap腔耦合理論 針對本項目提出的基于SNAP微腔的位移傳感方案,分析SNAP微腔的耦合諧振譜與耦合位置坐標的關系式。通過求解一維薛定諤方程得到SANP微腔耦合系統的透過譜理論表達式:
其中:
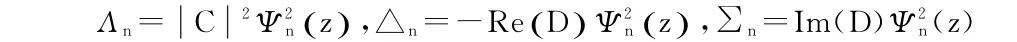
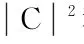
3 仿真結果分析


圖2 特定耦合參數下的諧振譜圖,S(0)=0.95-0.01i
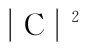
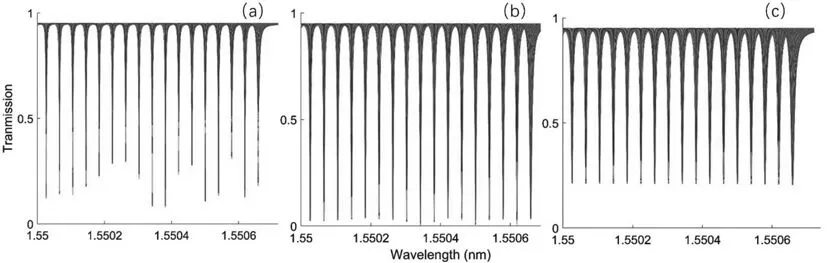
圖3 不同耦合參數下的歸一化透過率譜圖,(a)D=0+0.010i,(b)D=0+0.015i,(c)D=0+0.02i,
3.2 有效半徑變化參數對諧振譜的影響 首先我們研究了SNAP微腔的曲率對軸向自由頻譜范圍的影響。計算中取諧振范圍從1.55000μm到1.55072μm,我們發現當?k翻倍變化,后者是前者的2倍,即?k從120增加到960的過程中,相鄰模式之間的波長逐漸增大。在傳感實際應用過程中較大的自由頻譜范圍表示模式之間的間隔大,相鄰模式之間不會重疊,進而后期編碼的復雜度和識別的錯誤率就會降低。但是若FSR太大,將意味著掃描相應數量的模式需要的頻率掃描范圍更大,在實際應用中對儀器的精度是巨大的考驗。這里經過綜合考量,我們選擇?k=120。
圖4給出了SNAP-光纖錐耦合系統透射譜在?k=120情況下的前7階透過率-Z曲線圖,在圖中,對于一階模式,在耦合位置從z=0μm到z=200μm變化的過程中,透過率經歷了從小再到大的單調過程,其測量范圍只有透過率單調陡峭變化的部分;同理,對于n階軸向模式則會經歷n次類似的變化歷程。由此可見,隨著自由頻譜范圍的變小,模式數量的提高,在高階模式中,透過率陡峭變化區域較多,可實現多段高靈敏度位移測量,但是依舊無法實現連續大范圍 高靈敏度位移傳感。所以,利用單個階數無法實現大量程位移傳感,只有多階軸向模式一起綜合利用才可以。
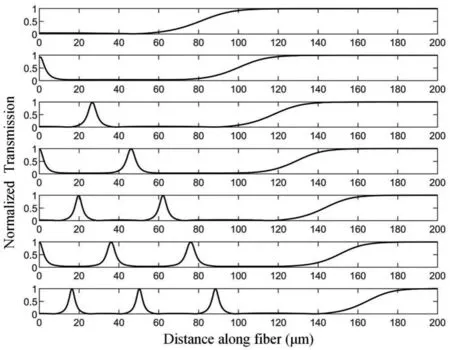
圖4 透過率——z曲線圖,?k=120
4 結論
為了獲得大量程、高分辨率和良好穩定性的微位移傳感,本文提出了一種基于微腔的新型位移傳感方案。對SNAP結構微腔-光纖錐耦合系統的位移傳感特性進行了研究,仿真計算繪制了不同耦合位置諧振譜圖,并分析了參數和諧振譜特征之間的關系。本文所得到的結論對SNAP微腔諧振譜圖對于傳感的試驗參數設計有指導作用。

