NACA埋入式進氣口氣動特性試驗設計優化

朱德軒，楊 旸，余志健，李志鵬，張 冬

(1.中國商飛上海飛機設計研究院，上海 201210；2.中國科學院工程熱物理研究所南京未來能源系統研究院，南京 210000；3.中國科學院工程熱物理研究所先進燃氣輪機實驗室，北京 100190)

民航飛機飛行時燃油箱需要與外界大氣連通以保證油箱結構的安全。同時，飛機惰化系統和環控系統也需引入外部冷卻空氣以滿足系統運行需求。對于民航飛機來說，目前主要有兩種進氣口設計，分別為戽斗式進氣口和埋入式進氣口。與戽斗式進氣口相比，埋入式進氣口沒有外部突出物，降低了對飛機氣動阻力的影響。同時無需支撐加固結構，重量較輕。埋入式進氣口主要為(美國)國家航空咨詢委員會(National Advisory Committee for Aeronautics，NACA)埋入式進氣口，該種進氣口已在波音、空客及中國商飛等若干機型上得到廣泛應用。

NACA埋入式進氣口，通過側邊產生一對軸向渦，將壁面氣流卷吸入進氣通道[1]。但由于進氣口通常位于較厚的邊界層內，吸入的為邊界層中低能氣流，導致進氣流量減少及出口氣流不均勻度高[2]。同時由于飛機在高馬赫數(Ma)下飛行，在NACA進氣口前部喉道位置容易產生激波，增加氣動阻力，惡化氣動性能。

因而，需對NACA進氣口進行氣動優化設計。徐尚成等[3]將一體化設計方法應用于進氣道設計, 采用特征線法設計了5種不同型面的前體。喬文友等[4]提出一種基于前體激波形狀的一體化設計方法，以使進氣道捕獲截面和唇口型線與飛行器前體激波匹配。李怡慶等[5]對圓錐流場在不同攻角條件下的氣動特征進行分析, 以流線追蹤技術為基礎，發展了一種曲錐前體/三維內轉進氣道一體化設計方法, 獲得了3個幾何參數對一體化方案外形和性能的影響規律。為設計低噪聲進氣道，邱昇[6]提出了一套基于聲學伴隨方法和梯度增強代理模型的高效優化設計框架。李靜等[7]提出了一種三維進氣道沿程結冰參數分析方法，并考察了進氣道參數對結冰的影響。在實際進氣道工程設計上，上海飛機設計研究院薛勇等[8]基于試驗數據獲得的進氣口總壓恢復系數和截面捕獲流量比關系，確定飛機極熱天巡航狀態設計工況點，而后根據NACA推薦尺寸比，確定最終尺寸。王赟等[9]提出在滿流量基礎上以燃油代償損失為綜合評價指標進行設計。

國外Soltani等[2]對超音速混合壓縮進氣道進行了實驗研究。以總壓恢復系數、質量流率和流畸變為進氣性能指標。結果表明，應用邊界層抽吸上游的攝入量喉嚨可以大大提高進氣性能的設計和非設計工況條件而不影響進氣質量流量。Javed等[10]采用計算流體力學方法計算了超燃沖壓發動機引擎進氣系統的質量捕獲率。

現有進氣道設計研究主要針對超聲速或發動機進氣道，考慮減小發動機前進氣畸變。設計中兼顧進氣道進氣噪聲及結冰等特性。對于民用客機公用系統進氣道研究較少。各結構參數對客機公用系統進氣道性能參數影響特性研究較少。工程設計上直接采用基于邊界層的理論公式計算進氣口參數，各關鍵幾何尺寸采用NACA早期推薦值，各幾何參數的具體影響機制和作用機理無法解析。且對于非平行面組成的進氣口，斜坡底部的流動發散，且外流不平行于斜壁，有渦形成，理論模型精度不足。

為解決上述問題，現采用計算流體力學(computational fluid dynamics,CFD)方法建立民機公用系統NACA埋入式進氣口數值模型，對其氣動特性進行分析，并以阻力、總壓恢復系數、出口質量流量和出口馬赫數為性能指標進行幾何參數優化設計。首先，理論分析確定幾個關鍵的進氣口幾何控制參數，通過試驗設計(design of experiments，DoE)方法進行參數優化，通過統計回歸找出最優的幾何參數組合結構。并對試驗設計結果進行方差分析(analysis of variance, ANOVA)[11]，分析出各控制參數各自及相互影響規律。同時基于CFD計算結果詳細研究各幾何控制參數對進氣口速度、壓力分布、渦強度及流線等氣動特性影響機理，最終獲得具有最佳氣動特性的進氣口幾何結構參數。

1 數值方法

1.1 幾何及邊界條件

所用的NACA進氣道幾何結構如圖1(a)所示，由進氣口、斜坡、轉角及尾通道組成。基準工況：出口尺寸68 mm×24 mm，斜坡高30 mm，轉角外半徑30 mm，內半徑10 mm, 出口高度232 mm。整體計算域如圖1(b)所示，坐標原點位于進氣口前緣尖角位置，計算域進口距離前緣尖角1 m，通氣口后1 m結束，側面各留0.5 m長，向下擴展0.7 m。氣流經過NACA通氣口后拐角轉90°向上連接火焰抑制器，計算采用直通口，并預留一定長度直通道。進氣口附近表面為壁面，主流計算域四周及底面采用壓力遠場邊界，進氣口出口為壓力出口邊界條件。主流參數如表1所示。

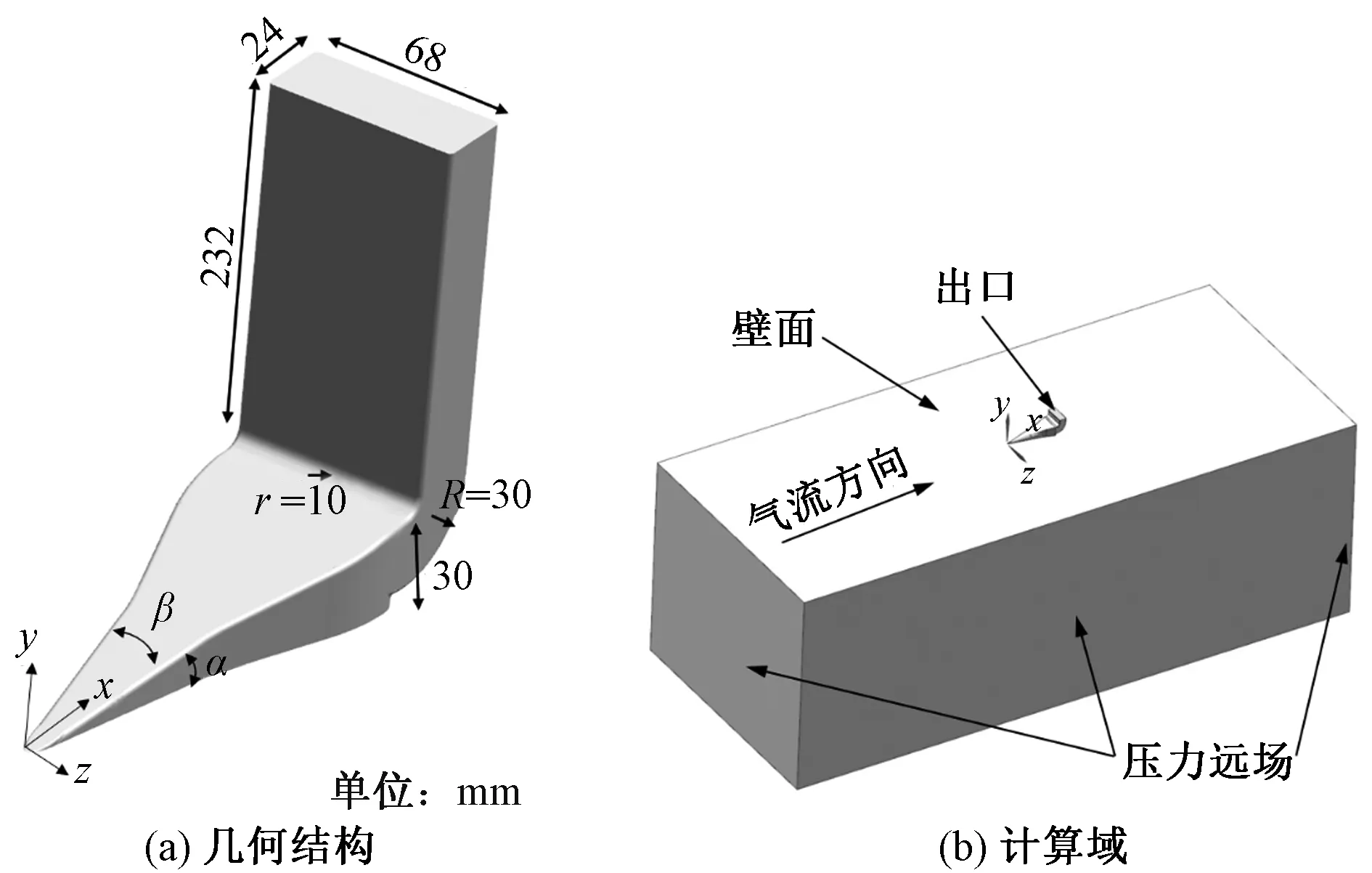
α為斜坡角度；β為斜坡錐角；r為內折轉半徑；R為折轉角半徑

表1 主流參數

1.2 網格與網格無關性

主流壁面和NACA進氣口壁面采用3層棱柱層網格，網格第一層高度分別為0.025 mm和0.02 mm，保證無量綱壁面距離y+≈1[12]，由于選用k-omega SST(shear stress transfer)湍流模型，僅研究型面的影響，選擇巡航設計點作為單一邊界條件，因此對于不同計算工況采用同一套網格分辨率劃分。對整個計算域進行分區劃分混合網格。對于NACA進氣口及進口向下10 mm單獨分區采用空間分辨率1.25 mm的結構化多面體網格；進氣口四周一定范圍單獨分區采用分辨率4 mm的結構化多面體網格；其他區域采用分辨率15 mm結構化多面體網格。結構化網格以及邊界層網格的交界面處，采用了非結構網格進行填充。由于NACA通氣口為邊界層進氣，非結構填充將極大減小求解過程的數值耗散問題。整體網格劃分和局部網格細節如圖2所示。

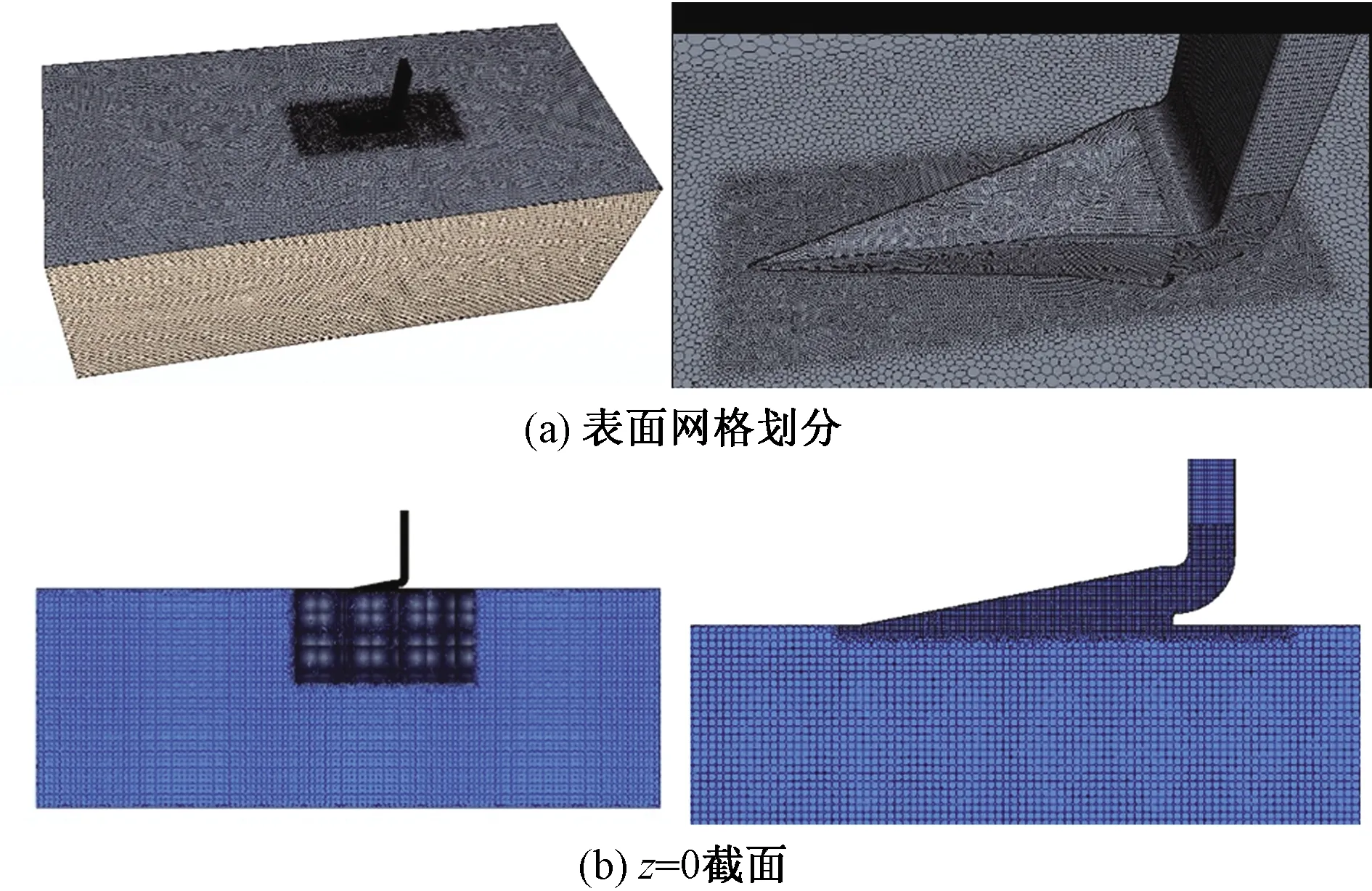
圖2 整體和局部網格劃分

對網格進行無關性驗證。在不改變壁面棱柱層網格高度的情況下，對劃分的3個區域分別進行加密，使得主流、靠近通氣口區域及通氣口內部包含折轉部分增加和減少20%的節點，分別劃分出110萬、197萬和297萬三套網格。

圖3、圖4和圖5為不同網格數量下進氣口軸向渦發展截面(x=0.08 m)x方向、y方向及z方向速度分布。x=0.08 m處，邊界層開始有向進氣口內部發展趨勢，兩個軸向渦已經發展完成。將197萬的網格進一步加密到297萬，并不能明顯改變速度分量沿展向的數值，但加密后計算的速度分布還是有輕微的變化，由于297網格不算太多，因此后續將采用297萬網格策略。

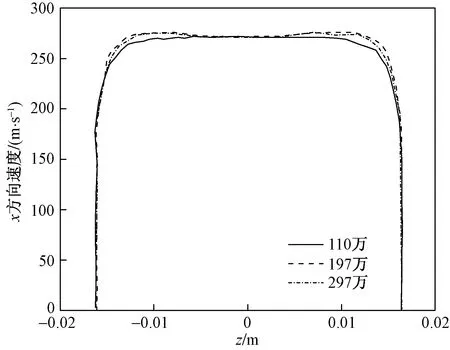
圖3 不同網格數量下截面(x=0.08 m)x方向速度分布對比

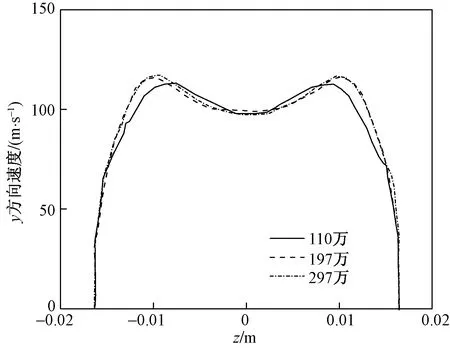
圖4 不同網格數量下截面(x=0.08 m)y方向速度分布對比

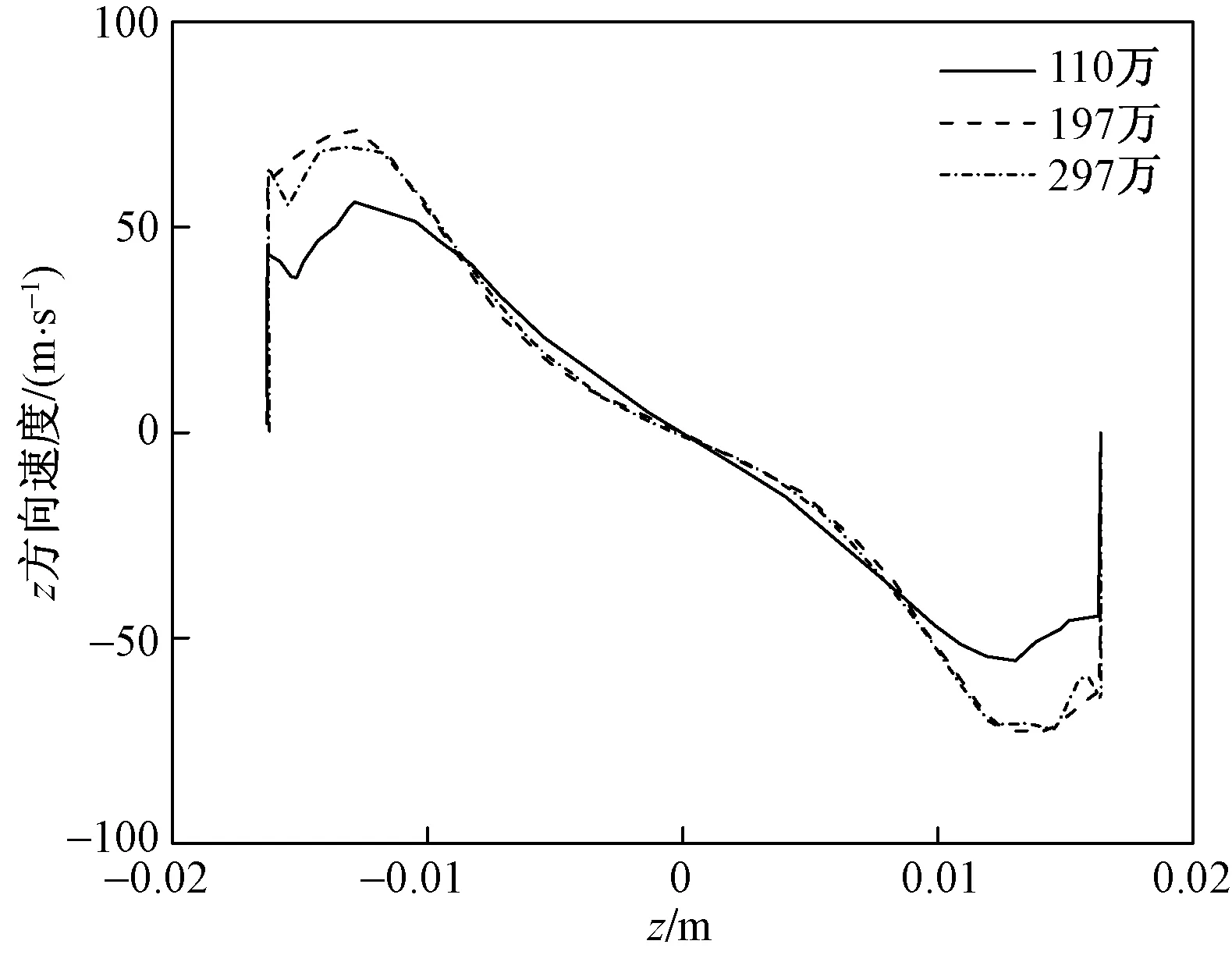
圖5 不同網格數量下截面(x=0.08 m)z方向速度分布對比

1.3 數值方法

穩態RANS(Reynolds-averaged Navier-Stokes)計算采用k-omega SST湍流模型，并采用密度基求解器求解。密度采用理想氣體定律，比熱容采用分段多項式，動力黏度采用Sutherland模型。湍流動能和湍流耗散率采用二階迎風格式離散，操作壓力選為零值。壁面均為絕熱條件。

1.4 DoE設計

根據三角翼[13]與四面渦發生器[14]理論，進口坡度對軸向渦產生有重要作用，而對于NACA進氣口需加強軸向渦還是減弱軸向渦，文獻暫未給出結論。現有NACA通氣口側邊根據文獻[15]設計，而NACA原始文獻中，該形狀是從三角形出發，依據減少進口展向角度修型獲得。對于型面設計是否影響進氣口氣動性能未有詳細分析。

如圖6所示，NACA進氣口斜坡形狀可以簡化成兩個三角形，并用光滑曲線進行連接[16]。根據型面曲線結果，β可保持不變以減少參數個數，且民航飛機巡航馬赫數低于1。

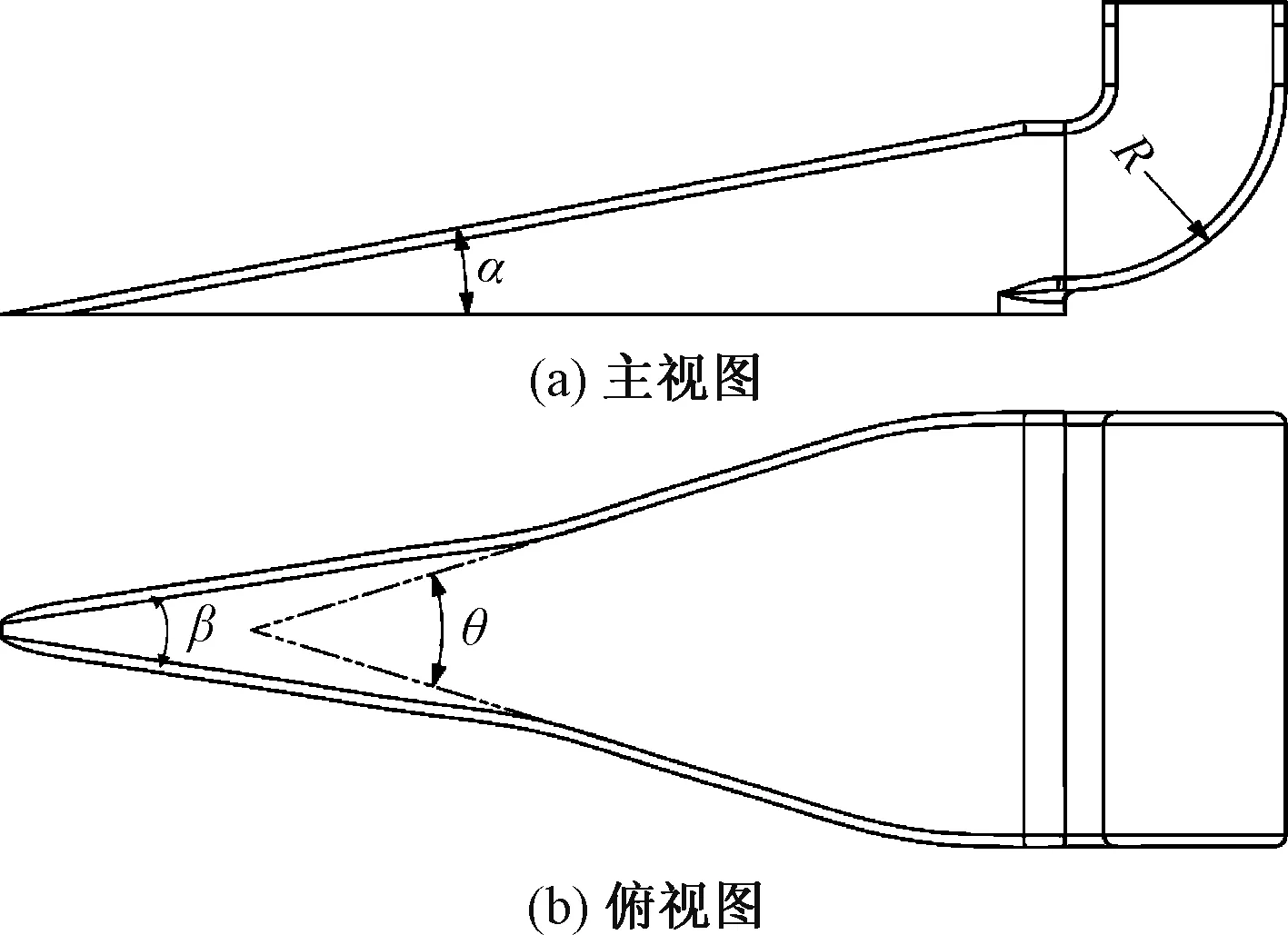
圖6 關鍵幾何控制參數

因此主要研究進氣口3個關鍵幾何參數，如圖6所示分別為α、θ和折轉半徑R。在主流體域及網格策略不變的情況下，固定折轉角出口幾何尺寸及其下游幾何域進行試驗設計。對3個因素進行三水平設計，確定3個因素對性能的影響是否有非線性；再從中篩選出8個算例，對三因素-兩水平結果進行方差分析，獲得主要影響參數。三因素-三水平取值分析如下。

(1)α。該角度為斜坡角度。在保證折轉角不變的情況下，增大該角引起進氣口整體縮短。根據三角翼以及四面體渦發生器理論，該角度直接影響軸向渦的形態。主流進氣有3°的攻角，而一般平板邊界層分離擴散角為11°，因此選取11°、13°、和15°共3個幾何變量水平，相應的，主流對斜坡的氣動攻角為8°、10°和12°。

(2)θ。該角度為斜坡擴張角，決定斜坡型面拐點位置。θ小則拐點靠近前緣。在NACA報告中沒有對此的描述，而是用光滑樣條曲線連接了出口與前部三角形。為了量化該型面，采用θ來控制拐點位置，取值范圍為36°、40°和44°。

(3)折轉角半徑R。在保證出口位置一定時，該弧度會影響進氣口的阻力以及轉向時因面積變化導致的流道內馬赫數變化。R的取值為32、40和44 mm。

三因素-三水平的試驗設計表如表2所示。

表2 水平試驗設計表

1.5 性能參數指標

選取如下4個性能參數指標作為試驗設計的因變量。

(1)阻力D。該阻力為作用在NACA進氣口斜坡、斜坡側面以及所有轉角面的總摩擦力與壓力之和，采用絕對值。

(2)總壓恢復系數。定義[15]為

(1)

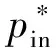
(3)進入進氣口的質量流量m，為斜坡出口拐角前截面數據。

(4)斜坡出口拐角前截面平均馬赫數。

2 結果與分析

2.1 基準工況

圖7為基準工況下進氣口表面極限流線和靜壓分布圖。可以看出，在1/2軸向位置的側面上有低壓區，而靠近進氣口折轉角位置處靜壓恢復。

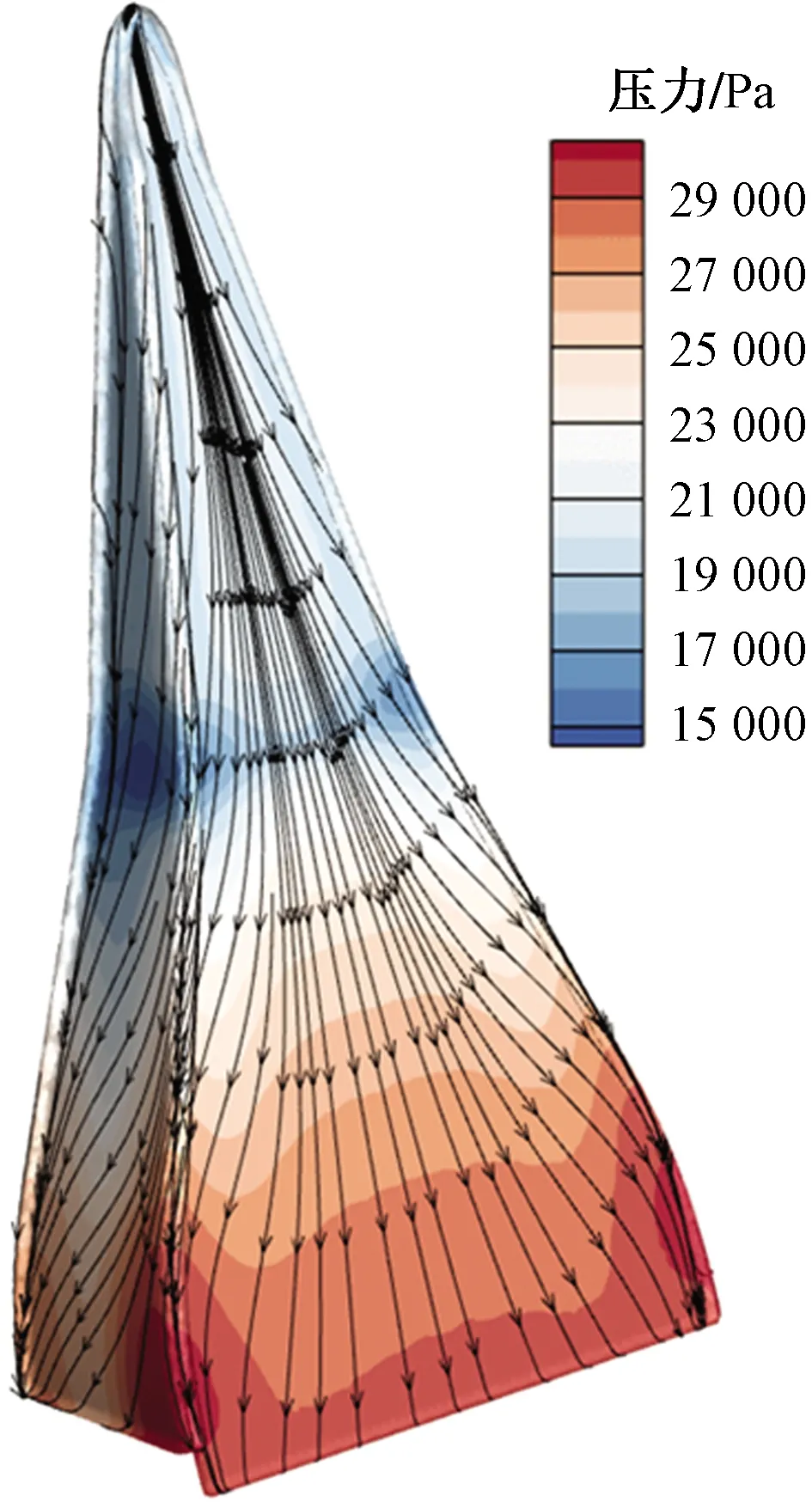
圖7 基準工況進氣口表面極限流線和靜壓分布圖

表面極限流線表明斜坡底部沿流向流線呈現分散趨勢，因此在底部無分離。在側面靠近通氣口底部的側邊，通氣口底部流線在此聚集；在側面靠近主流的一面，側面流線在此聚集，因此可以推斷，主流在側邊卷起軸向渦，并向下游發展。但是這個軸向渦并不貼靠在斜坡底面，否則斜坡底部將會有流線匯聚的現象。

為更形象地分析軸向渦，選取渦量為1.03×108s-1的等值面并用靜壓染色進行分析，如圖8所示。軸向渦從NACA進氣口前緣形成，并且始終靠近斜坡側面與主流相交的側邊，而不靠近斜坡的底部，因此推測側邊的主流與進氣口內部壓差，以及側邊帶來的速度間斷面是產生軸向渦的關鍵，如果希望增強軸向渦，就需要增大壓差與間斷面，即增大斜坡角并盡量減少側邊的倒角。側邊倒角受制造工藝影響，而斜坡角α是可以設計的。觀察兩支軸向渦，發現在靠近進氣口處靜壓較低，而在斜坡側邊拐點處，渦管上靜壓陡升。在側邊形成的軸向渦繼續向下游發展，通過90°轉角延伸至出口，而且越向下游，兩支渦管越有相互靠攏的趨勢。在轉角附近，速度方向發生變化，該處可被Q渦識別方法捕獲，并具有較低靜壓。

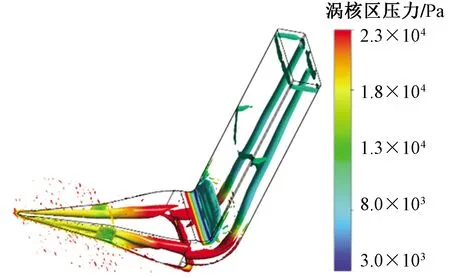
圖8 渦核區靜壓染色圖

2.2 DoE結果

DoE 27個算例求解的性能參數如表3所示。可以看出，在斜坡角α為15°的所有組合中，進氣口出口馬赫數均超過1，而在α為11°的所有組合中，出口馬赫數均小于1，當α為13°時，則兩種情況均有。當馬赫數超過1時，跨過激波面總壓損失增大，速度降低，靜壓升高。單就氣動損失而言，是不利的，然而這也是一種短距離內快速降低流入進氣口速度的方法。以表3中第2(α=15°)與第27(α=11°)工況為例，在其他參數不變時，盡管高α角(第2個工況)總壓恢復系數較低α角的工況縮小了11.12%，阻力降低了9.62%，但低α角流入通氣口的氣體流量增加了14.57%。

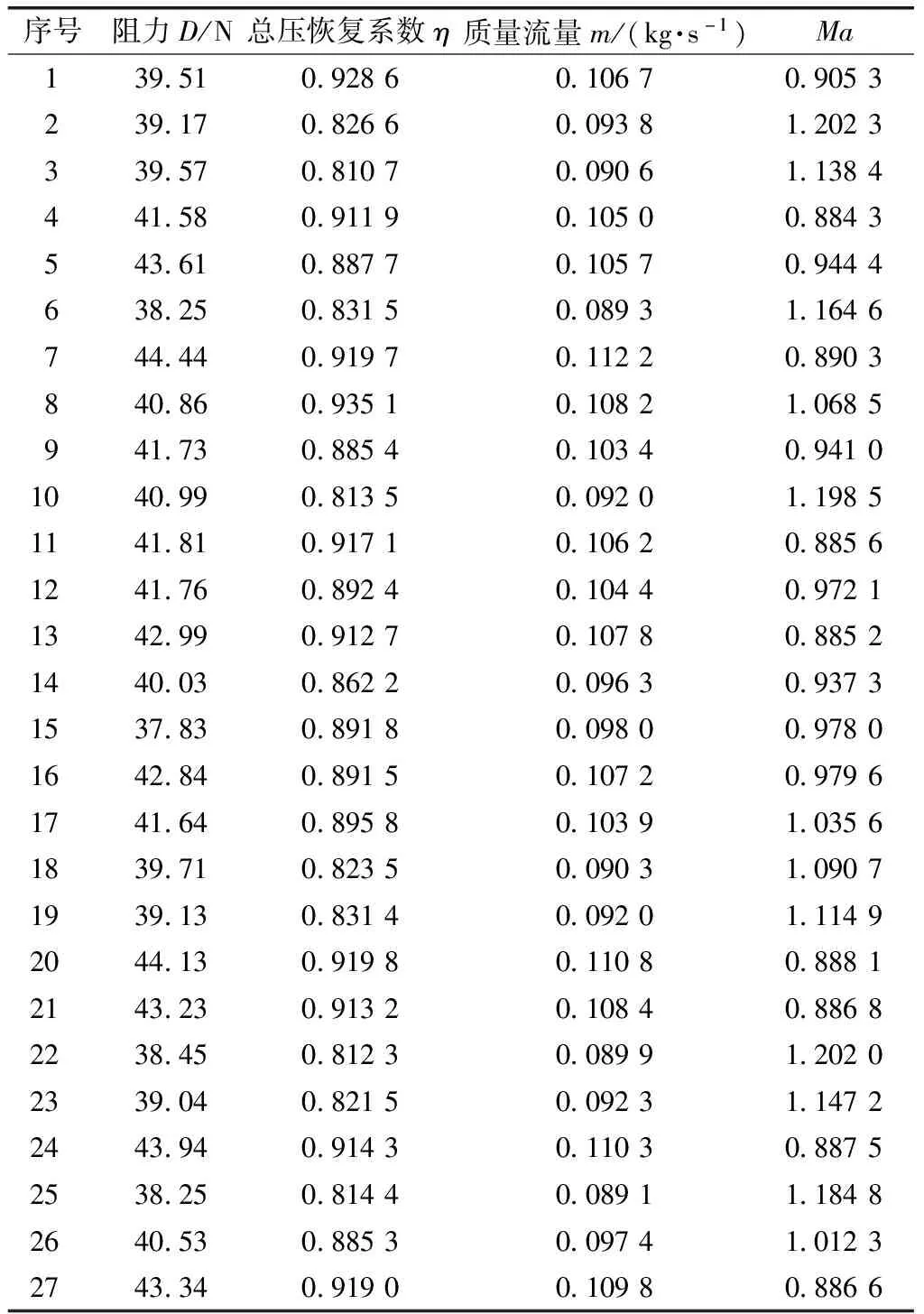
表3 DoE算例計算結果

對表3數據進行三因素-三水平的方差分析，各因素對各性能參數的主效應和交互效應如圖9和圖10所示。由圖9可以看出，θ對阻力有非線性的影響，由于整體影響偏小，且上下限相對平均值小于2%，該非線性影響基本可忽略。α對4個因變量影響較其他兩個參數影響大，隨著α增大，除了出口截面馬赫數外，其他參數值均減小。因此減小α對進氣口氣動性能提升有利。θ對4種因變量的影響在3個幾何參數中最小。除了阻力特性外，其他參數均隨θ增大而減小。出口轉折半徑R對阻力和流量影響大，且均隨著折轉半徑R增大而減小。

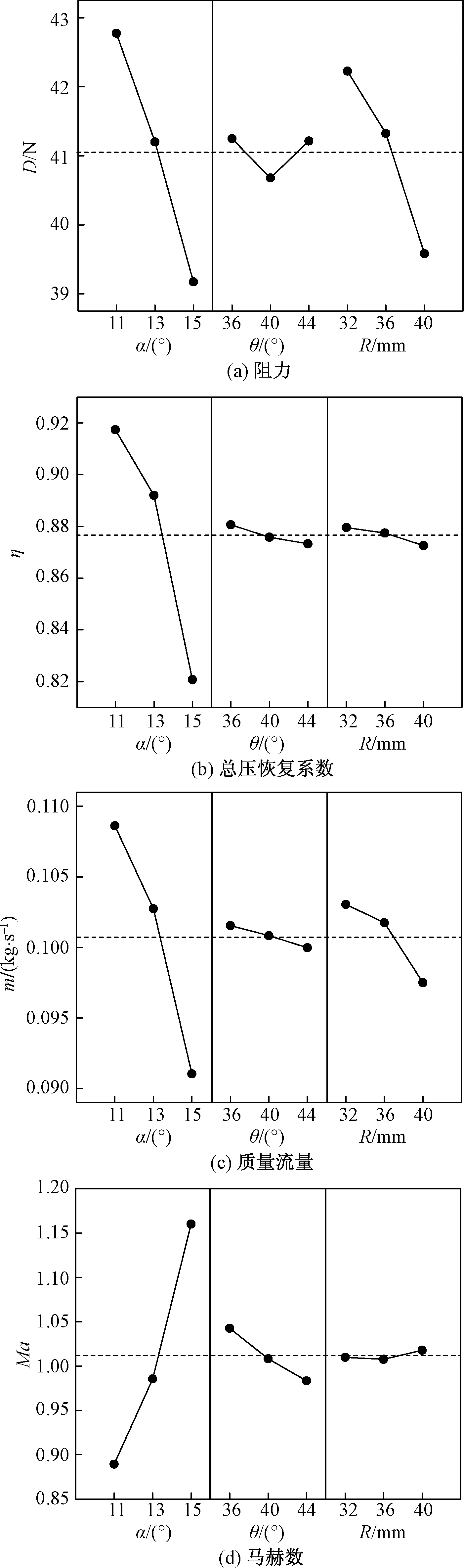
圖9 各因素對性能參數主效應影響

從圖10交互效應可以看出，阻力和質量流量上α和θ與折轉半徑R相互影響效應強；總壓恢復系數上，各因素之間相互影響弱；出口馬赫數上，α和θ之間有相互影響。由主效應分析可知，α越小，總壓恢復系數和流量越大，進氣口性能越好；而后根據交互效應，在α一定時較小的折轉半徑和θ對這兩個參數有利。表3中工況7和工況27為兩個極端參數工況，可見工況27性能較佳。

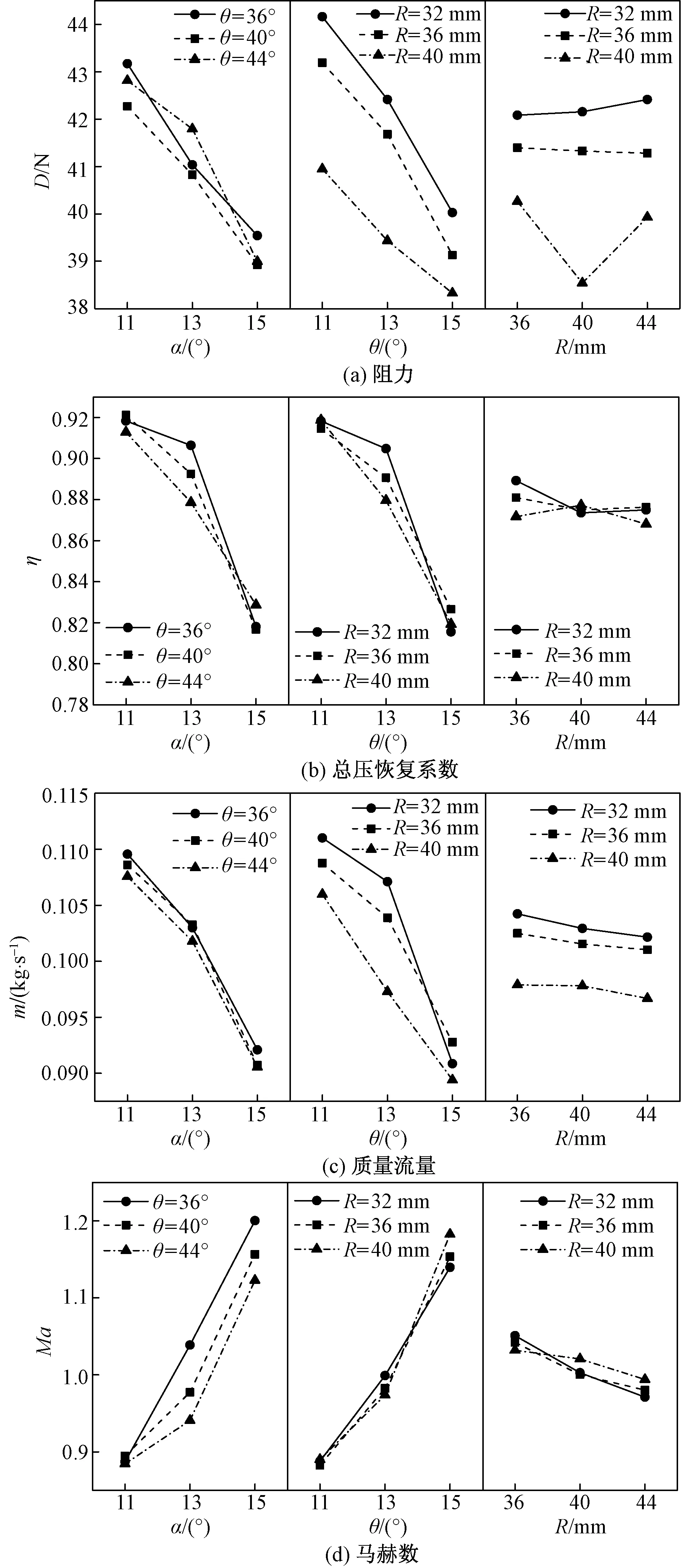
圖10 各因素對性能參數交互效應影響

2.3 工況2 和工況27結果對比

由圖9可知，α對進氣口氣動特性影響大，且較小α、θ和折轉半徑R性能較佳，并進一步比較工況2和工況27性能指標，可得α=11°、θ=11°和折轉半徑R=36 mm的工況27進氣口綜合性能最好。因而基于工況27(α=11°)和工況2(α=15°)，其他兩參數保持一致，進一步分析α角的影響機制。

圖11為進氣口渦核區馬赫數分布，α越小，進口越大，進氣口前緣氣流擠壓效果越弱，前緣位置馬赫數越小。

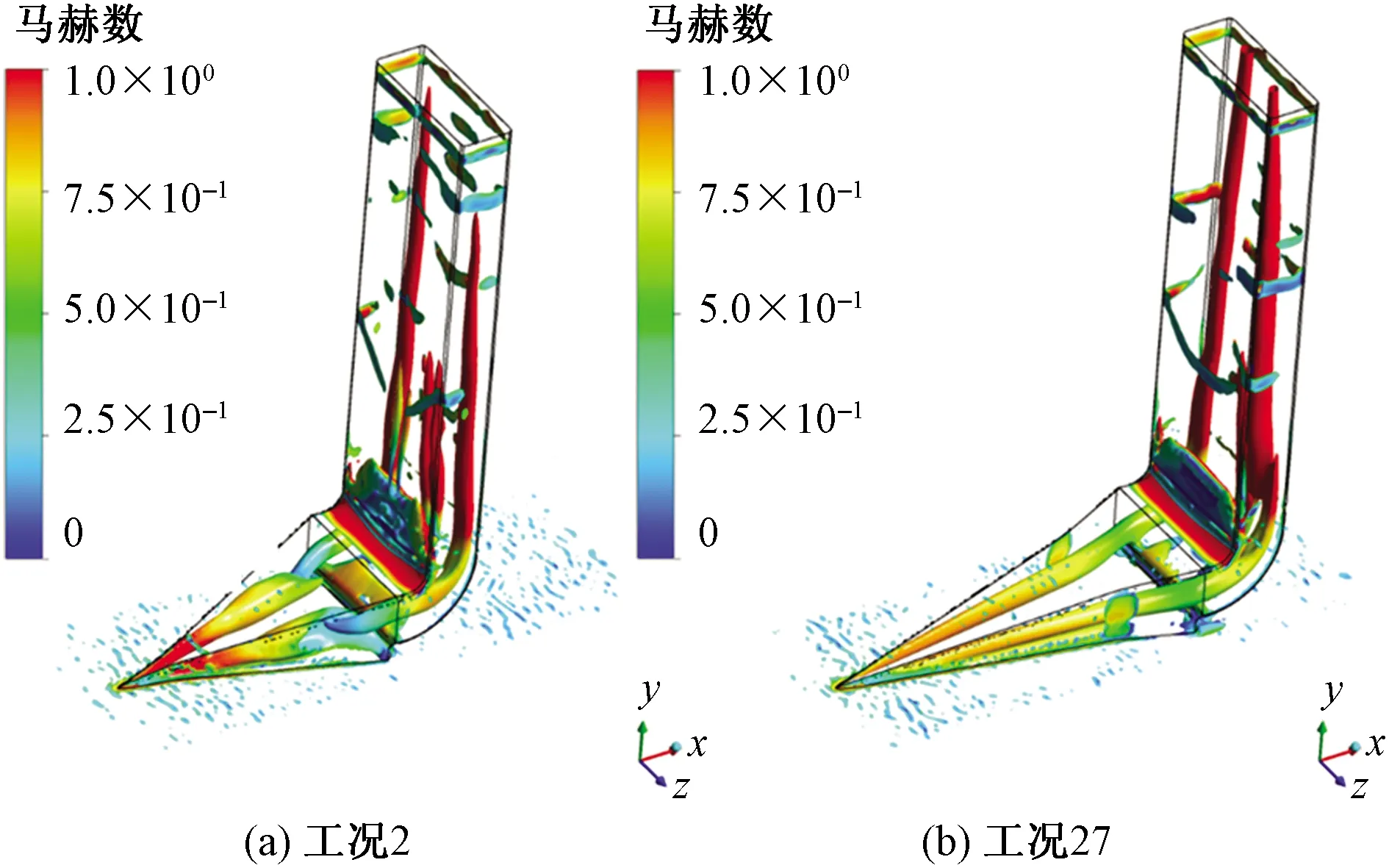
圖11 渦核區馬赫數分布

圖12為渦核區靜壓分布，α越小，進氣口前緣靜壓越大，對減弱壓損有力，斜坡處渦管越長，越有利于卷吸氣流，同時渦管向折轉通道下游延伸越長，有利于加強下游氣流摻混，進而利于出口氣流均勻度提升。

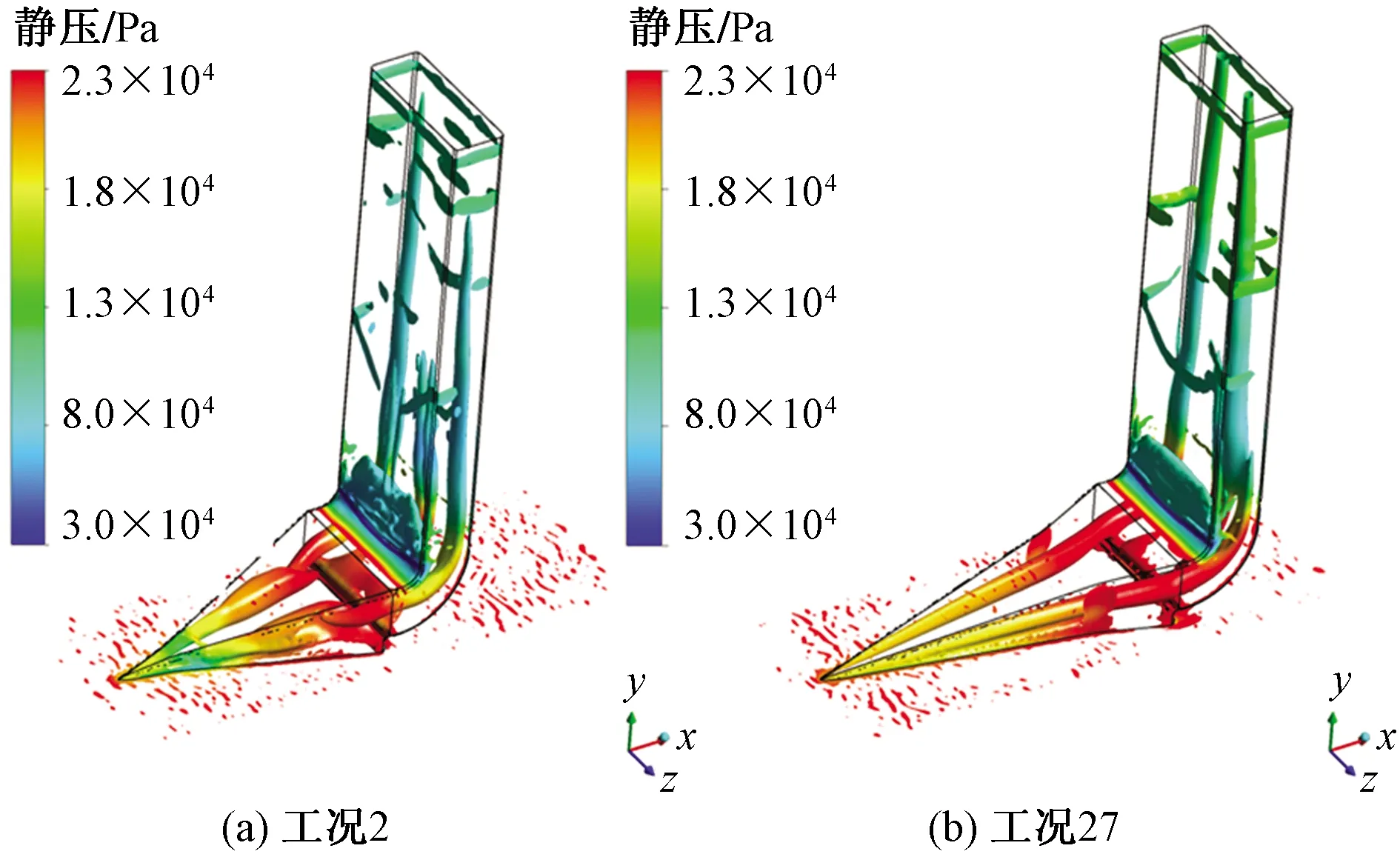
圖12 渦核區靜壓分布

圖13為斜坡各截面馬赫數分布，可以看出α越小，截面馬赫數分布越均勻，且數值越小。圖14 為流入進氣口流線及斜坡各截面速度分布云圖，可以看出α越小，相同位置截面速度分布越均勻。更加均勻的速度分布有利于減小出口畸變，提升進氣口進氣質量。從流線上看，α越小，壁面分離效果越弱，有利于減弱壓損和增加出口氣流均勻性。

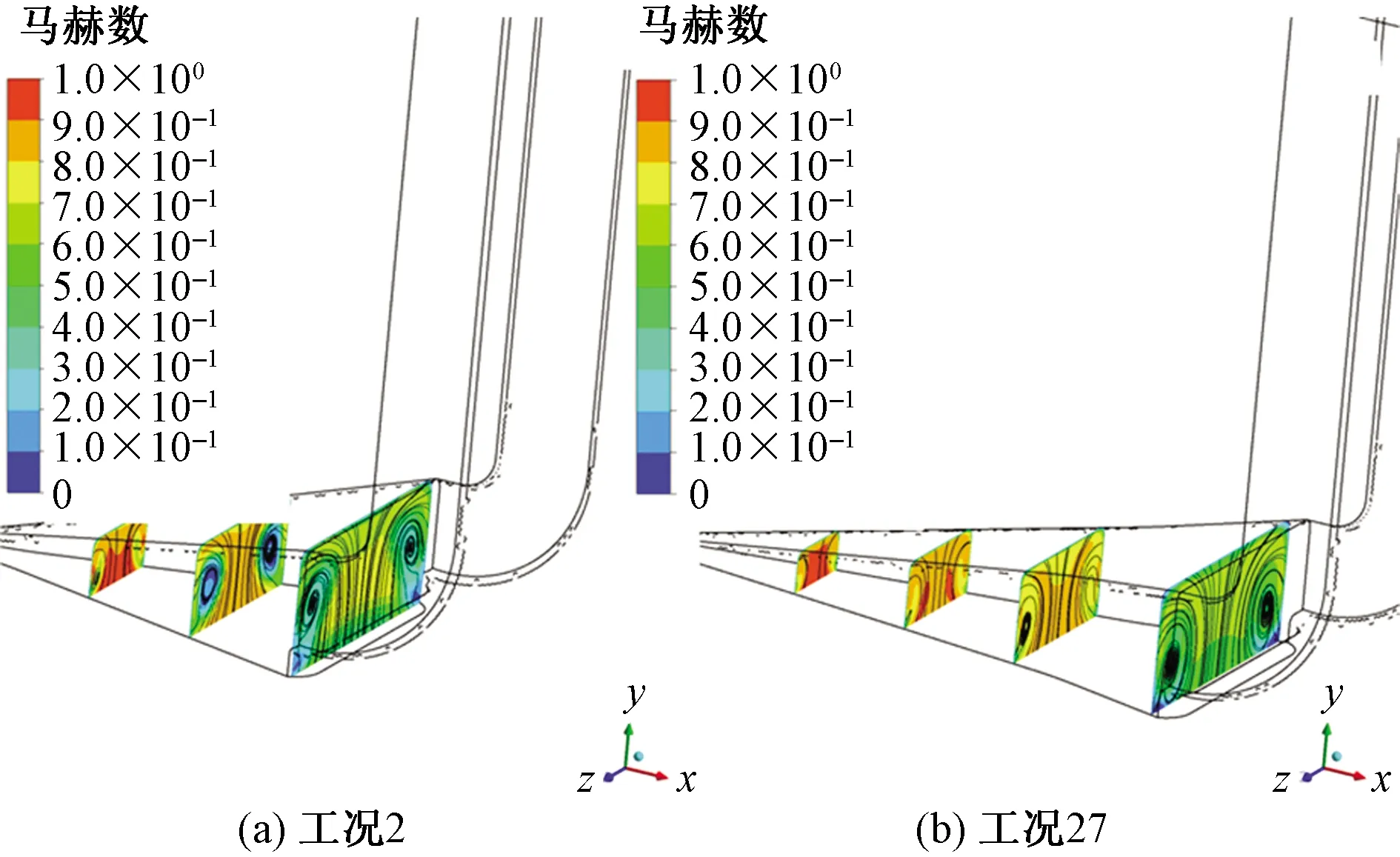
圖13 斜坡各截面馬赫數分布

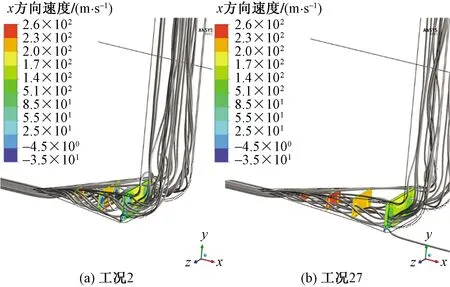
圖14 流入進氣口流線及斜坡各截面速度分布

3 結論

(1)進氣口軸向側面上有低壓區，在斜坡側邊靠近主流處有一對軸向渦，且越向下游，兩支渦管越靠攏。

(2)α對4個性能參數影響大，α增大，除出口截面平均馬赫數外，其他參數值均減小。θ對性能參數影響小。出口折轉半徑R對平均阻力和平均流量影響大，且均隨著R增大而減小。

(3)交互效應可得，阻力和質量流量上，α和θ與折轉半徑R相互影響效應強。α越小，總壓恢復系數和流量越大。而后根據交互效應，可確定較小的折轉半徑R和θ性能指標越好。

(4)α越小，前緣位置馬赫數越小，靜壓越大，同時渦管向下游延伸越長，同截面馬赫數和速度分布越均勻，壁面分離越弱，有利于減小壓損，增加卷吸氣流，減小出口畸變，提升進氣質量。

綜上分析，較小α、θ和折轉半徑R的性能較佳，并進一步比較工況2和工況27性能指標，可得α=11°、θ=36°和折轉半徑R=36 mm的工況27進氣口綜合性能最好。