FY?3（05）星主動對月定標控制技術研究

王金華，薄煜明，高旭東，尹海寧

（1.南京理工大學 自動化學院，江蘇 南京 210094；2.上海衛(wèi)星工程研究所，上海 201109；3.上海航天控制技術研究所，上海 201109）

0 引言

氣象衛(wèi)星的遙感儀器性能通常會隨著光學元件和電子元件的老化以及空間環(huán)境的變化而變化。工程經(jīng)驗表明，氣象衛(wèi)星的可見光、近紅外通道探測器靈敏度每年都有一定程度的衰減。這意味著，對衛(wèi)星遙感儀器進行在軌定標是非常必要的。目前，衛(wèi)星在軌定標源主要采用星上黑體、太陽光等，但黑體自身溫度的控制誤差、太陽光漫反射板的衰減會對星上定標造成不利的影響。以地物為目標開展定標時，大氣的確定性也會對在軌星上定標產(chǎn)生不利影響［1］。

除了傳統(tǒng)的定標手段外，在工程實踐中，月球作為一種在軌定標源也逐漸受到重視，主要是月球定標相對于其他定標手段有其獨特的優(yōu)勢。首先，月球具有極穩(wěn)定的反射比，輻照度年變化小于10?8，并且反射光譜是連續(xù)光滑的，能夠較好地反映太陽光譜的結構；其次，月球光譜輻亮度值在大部分衛(wèi)星遙感儀器的動態(tài)范圍之內(nèi)，不需要在光路中引入其他部件，可以簡化定標流程；另外，從衛(wèi)星運行的軌道來看，無論是常用的太陽同步軌道衛(wèi)星還是地球靜止軌道衛(wèi)星，都有較多機會在軌進行月球觀測，為不同衛(wèi)星之間的定標提供了統(tǒng)一的標準［2-7，9-10，12］。

FY-3（05）星是風云三號系列衛(wèi)星中首顆運行于晨昏軌道的太陽同步軌道衛(wèi)星，針對主載荷——中分辨率光譜成像儀的應用需求，首次設計了衛(wèi)星對月定標工作模式。中分辨率光譜成像儀在軌運行時，需要通過對月觀測進行儀器定標。目前在軌衛(wèi)星采用對地定向的姿態(tài)模式，月球每月進入中分辨率光譜成像儀視場一次，但由于月球矢量相對于衛(wèi)星軌道系+Y軸轉(zhuǎn)動，中分辨率光譜成像儀視場掃描月球圓盤的時間不足10 s，只能形成數(shù)幀有效圖像。為了增加中分辨率光譜成像儀對月球的觀測時長，本文提出了機動對月定標工作模式。在該模式下，衛(wèi)星本體姿態(tài)保持近似慣性定向，使中分辨率光譜成像儀視場能夠長時間觀測到月球。確定機動對月定標的控制目標，使月球在中分辨率光譜成像儀掃描視場內(nèi)停留超過30 min。

本文對FY-3（05）衛(wèi)星機動對月定標工作模式的相關情況進行了說明，總結了軌道、數(shù)管、姿軌控、熱控相關分系統(tǒng)的工作。姿軌控方案表明，機動對月定標模式能夠增加中分對月球圓盤的觀測時長。在機動對月定標過程中，平臺及載荷各分系統(tǒng)能夠適應外部環(huán)境變化。

1 對月定標方案

1.1 載荷視場分析

中分掃描視場的后視圖（即從軌道系原點指向+X軸方向）如圖1 所示。中分掃描視場是一個條帶狀視場，在跨軌跡方向很寬（正常模式對地視場為圖中的34.9°～145.1°），但沿軌跡方向視場僅0.685°。在最初的方案中僅19°～22°的冷空定標視場可用于對月定標，目前的方案為中分可以調(diào)整掃描方案（更改掃描起始位置），使得12°～140°均可對月定標。由于對月定標時月球位于+Y側(cè)，所以實際對月定標可用視場為12°～90°。

圖1 中分掃描視場Fig.1 Median scanning field of view

圖1 中，0°方向為軌道系的+Y方向，90°方向為軌道系的+Z方向（即對地方向）。FY-3（05）衛(wèi)星是晨昏軌道衛(wèi)星，太陽始終位于軌道系的?Y方向附近，即圖1 中的180°附近。

1.2 對月定標方法

衛(wèi)星正常在軌飛行一圈，衛(wèi)星指向月球的矢量會繞衛(wèi)星軌道系的+Y軸轉(zhuǎn)動一圈，如圖2 所示。圖中可見，只有當月球矢量位于YOZ平面內(nèi)時，月球才會位于中分視場中，由于月球矢量的轉(zhuǎn)動，該過程只能持續(xù)一小段時間。

圖2 對月定標指向角示意圖Fig.2 Schematic diagram of the pointing angle of lunar calibration

為了能夠讓月球始終處于中分掃描視場之內(nèi)，當月球矢量進入YOZ平面以后，可以讓衛(wèi)星本體按一個確定的角速度繞+Y軸轉(zhuǎn)動，該角速度即月球矢量在軌道系中繞+Y軸轉(zhuǎn)動的角速度。通過衛(wèi)星本體的轉(zhuǎn)動，保證了月球矢量始終位于YOZ平面以內(nèi)。

1.3 指向角的定義

為了便于分析對月定標過程中的角度關系，下面定義了如圖2 所示的兩個指向角：1）α角為星月矢量與軌道系+Y軸夾角，用于輔助判斷星月矢量是否滿足中分掃描視場要求；2）β角為星月矢量在軌道系XOZ面的投影與+Z軸夾角，用于引導姿控作俯仰機動。

2 軌道計算方案

2.1 月球運動特點

月球軌道運動的平面稱為白道面，將月球軌道面擴大和天球相交的大圓稱為白道。為了描述月球的軌道運動，可以和人造地球衛(wèi)星一樣，用6 個軌道根數(shù)表示。不同的是月球的軌道根數(shù)應在以地心、黃道和春分點為基準的地心黃道坐標系中描述（描述人造地球衛(wèi)星的軌道根數(shù)的坐標系一般是以地心、地球赤道和春分點為基準的地心赤道坐標系）。

月球的6 個軌道根數(shù)為：aL為半長軸；eL為偏心率為升交點黃經(jīng)為軌道傾角為近地點黃經(jīng)為歷元時刻月球的平黃經(jīng)。

上述前4 個根數(shù)與經(jīng)典軌道根數(shù)的定義一樣。近地點黃經(jīng)為首先沿黃道從春分點量至升交點，然后再沿白道量至近地點的角度之和；月球的平黃經(jīng)為首先沿黃道從春分點量至升交點，然后再沿白道量至月球的平位置的角度之和。

白道、黃道和地球赤道的相互關系如圖3 所示。圖中：r為春分點為白道相對于黃道的升交點；εS為黃道相對于地球赤道的夾角（即黃赤交角），

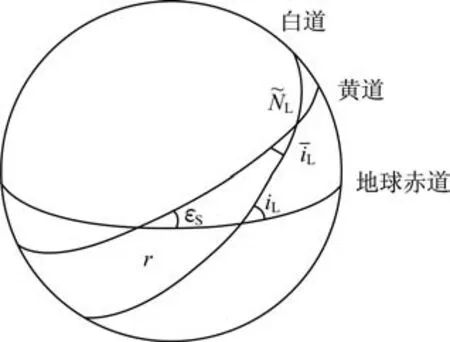
圖3 白道、黃道和地球赤道的相互關系Fig.3 Interrelation among moon’s path，ecliptic，and earth equator

由圖3 可知，由于交點西退引起白道與地球赤道的夾角iL發(fā)生變化。當升交點與春分點重合時，白道與地球赤道之間的夾角達到最大值：23°27′+5°09′=28°36′。當降交點與春分點重合時，白道面與地球赤道面之間的夾角達到最小值23°27′?5°09′=18°18′。因此，白道面與地球赤道面間的夾角在18°18′～28°36′之間變化，變化周期是18.6 a。

朔望月是以太陽位置為基準的周期。月球與太陽的相對位置不同而使月球的月相不同。月相為觀測者所看到的月球的相貌，如朔、望、上弦、下弦。陰歷初一為新月，稱為朔，十五或十六為滿月，稱為望，在朔望之間為弦，如圖4 所示。

圖4 月相的成因Fig.4 Reasons for the formation of moon phases

朔望月是月相連續(xù)兩次相同所經(jīng)過的時間，例如從新月到新月的周期或從滿月到滿月的周期。朔望月的平均長度為29.530 6 個太陽日，我國傳統(tǒng)的農(nóng)歷以朔望月作為月的單位。

2.2 月球矢量插值計算方法及精度分析

對月定標過程中需要計算月球位置矢量，常用的計算方法有解析法和插值法兩種。解析法的優(yōu)勢在于能夠遞推得到任意時刻的月球位置，但指向精度只能保證到0.1°左右；插值法的優(yōu)勢在于能夠提供高精度的月球位置，指向精度可以保證到0.001°，但有效的時間范圍只能保證1～2 d，不能遞推［8，11］。

考慮到衛(wèi)星對月定標的實際工作需求，采用插值法更為適合。一是因為對月定標的控制方案是一種開環(huán)控制（姿軌控分系統(tǒng)沒有月球敏感器，月球在中分辨率光譜成像儀視場中的實際位置不會反饋到姿軌控分系統(tǒng)），總的指向誤差余量只有0.092 5°，所以首先要求月球矢量計算盡可能不要引入誤差，把誤差余量留給姿軌控分系統(tǒng)；二是對月定標頻次較少（一年若干次），沒有必要時刻計算月球矢量，插值法僅需要在對月定標前上注12 個系數(shù)以及插值起始歷元即可。

2.2.1 插值算法

利用三次多項式計算月球在J2000 地心坐標系下的坐標：

式中：px1，px2，…，pz4為12 個插值系數(shù)；t為相對于插值歷元點的分鐘數(shù)（假設歷元時間為2019-04-26T00：00：00.000，需要計算的時間點為2019-04-26T00：01：30.000，則相對于歷元點的分鐘數(shù)為1.5，即式中t用1.5 代入）；t為星上數(shù)管軟件的計時時間，同真實時間之間存在20 ms 左右的偏差，在后文指向精度分析中考慮了該誤差。

當明確了中分對月定標的日期后，衛(wèi)星總體方根據(jù)該日期，利用STK 中的JPL/DE 星歷仿真出月球矢量在1 d 內(nèi)的J2000 位置坐標（共1 441 個數(shù)據(jù)點）；然后利用Maltab 中的曲線擬合工具cftool，采用三次多項式分別對x、y、z進行擬合，擬合系數(shù)使用雙精度浮點數(shù)，有效位數(shù)保證在15 位左右。擬合系數(shù)共12 個，每一個坐標4 個系數(shù)，即前文中的px1，px2，…，pz4，該系數(shù)在實施中分別對月定標前上注到數(shù)管計算機，同時還需要將擬合區(qū)間的初始時間t0上注到數(shù)管計算機，初始時間t0的格式符合數(shù)管現(xiàn)有計時格式（即相對J2000 的日計數(shù)和日內(nèi)毫秒計數(shù)）。

數(shù)管軟件需設置一個標志位，當該標志位有效時，啟動月球矢量的插值計算，否則還是使用之前的解析公式計算月球矢量。

2.2.2 插值精度

利用STK 中的DE 星歷計算了月球在1 d 之中的位置矢量，然后針對x、y、z坐標分別進行三次多項式擬合，比較了擬合結果和真實位置矢量之間的偏差。結果表明，x坐標最大偏差為0.3 km，y坐標最大偏差為0.3 km，z坐標最大偏差為0.14 km。其中，0.3 km 對應的角度誤差約為0.000 045°，能夠滿足高精度月球矢量的計算需求。

實際操作時，擬合區(qū)間也可以取2 d，這樣插值精度會略微降低，約為0.000 75°，但擬合系數(shù)的有效范圍可以延長1 d。

3 姿態(tài)控制方案

3.1 衛(wèi)星姿態(tài)控制方案

衛(wèi)星姿軌控分系統(tǒng)主要由測量部件、控制部件和執(zhí)行部件組成。其中，姿態(tài)測量部件包括星敏感器、紅外地平儀、陀螺、磁強計和太陽敏感器等；控制器為雙CPU 的姿軌控計算機；執(zhí)行機構包括偏置動量輪、反作用飛輪、磁力矩器和推力器等［13-16］。

該低軌氣象衛(wèi)星采用三軸穩(wěn)定偏置動量控制方式。為實現(xiàn)高可靠高精度姿態(tài)控制，系統(tǒng)穩(wěn)態(tài)運行階段采用“雙星敏感器+地平儀+飛輪”組合的三軸閉環(huán)控制方案，采用“陀螺組合+星敏感器+飛輪”實現(xiàn)俯仰機動360°完成對月定標觀測控制任務［14］。

為保證系統(tǒng)可靠性，采用如圖5 所示的飛輪配置及安裝方式，包含2 臺68 N·ms 偏置動量輪，1 臺6 N·ms、2 臺25 N·ms 反作用飛輪以及1臺68 N·ms 角動量補償輪。2 臺68 N·ms 偏置動量輪A、B 安裝在俯仰軸上，反作用飛輪D、E 分別正交安裝于偏航軸和滾動軸上，C 為備份反作用飛輪，其安裝軸與滾動軸正方向、偏航軸負方向夾角均為45°且在OXZ平面內(nèi)，1 臺68 N·ms 補償輪安裝在偏航軸上。

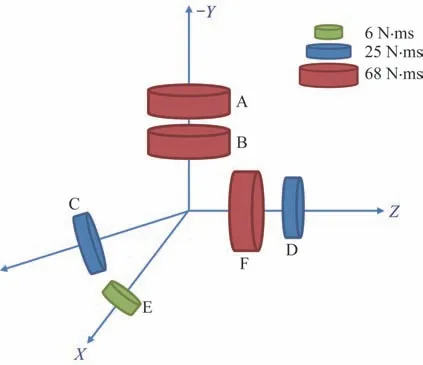
圖5 飛輪配置示意圖Fig.5 Schematic diagram of flywheel configuration

各飛輪在本體系下飛輪的安裝矩陣為

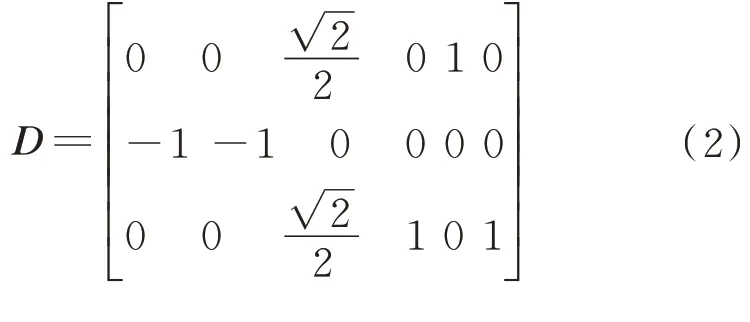
3.2 跟蹤控制器設計

對月定標采用跟蹤給定姿態(tài)角的方式進行跟蹤控制，給定姿態(tài)角為月球矢量在本軌道系XOZ面內(nèi)的投影與軌道系+Z軸的夾角β，由數(shù)管計算，作為控制器的輸入?yún)?shù)。當月球矢量在衛(wèi)星本體坐標系+X方向半平面時，β定義為正；當月球矢量在衛(wèi)星本體坐標系?X方向半平面時，β定義為負。衛(wèi)星繞俯仰軸轉(zhuǎn)動對β進行跟蹤實現(xiàn)對月定標。所設計的控制律由誤差姿態(tài)動力學模型得到。由于跟蹤過程的起始階段是一個長時間的動態(tài)過程，積分項I會帶來較大滯后，造成積分飽和影響系統(tǒng)穩(wěn)定性，所以在整個對月定標期間不接入積分控制。具體的控制算法如下：

無陀螺角速度信息為

式中：Kpx、Kpy、Kpz為XYZ軸比例控制系統(tǒng)；Kdx、Kdy、Kdz為XYZ軸微分控制系統(tǒng)；Tmgx、Tmgy、Tmgz為XYZ軸的磁卸載前饋力矩；Tdx、Tdy、Tdz為XYZ軸的干擾力矩前饋；令qe=[qe0qe1qe2qe3]T為誤差四元數(shù)，可表示為參考姿態(tài)四元數(shù)qoc（對月跟蹤的目標姿態(tài)，參考系相對于軌道系）和當前姿態(tài)四元數(shù)qob的四元數(shù)差。

qoc通過β計算得到，公式為

qob為衛(wèi)星本體系相對于軌道系的姿態(tài)四元數(shù)，由星敏測量姿態(tài)經(jīng)過姿態(tài)結算給出。

qe計算公式為

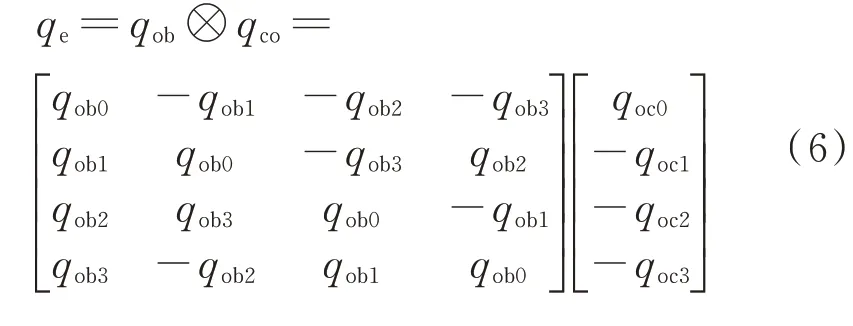
3.3 陀螺積分器設計

衛(wèi)星繞俯仰軸轉(zhuǎn)過一定角度后，受地球和星敏安裝角度的影響，會出現(xiàn)3 臺星敏全部失效的情況（持續(xù)約20～30 min），此時需要以最后一次有效的星敏數(shù)據(jù)作為姿態(tài)積分初值，通過光纖陀螺給出的角速度信息進行四元數(shù)積分得到當前衛(wèi)星姿態(tài)。

四元數(shù)運動學方程可寫為

通過k時刻的姿態(tài)四元數(shù)和陀螺角速度可以得到k+1 時刻的四元數(shù)，采用四階Runge-Kutta 法的高精度積分公式為

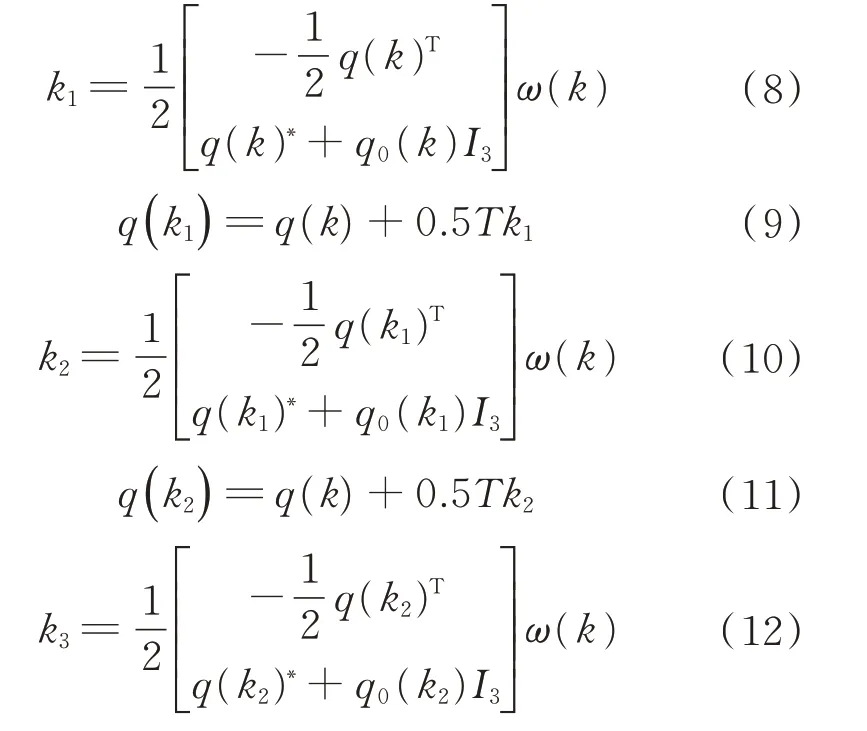
式中：T為陀螺積分的步長。

4 半物理仿真

仿真輸入條件如下：

仿真初值：三軸姿態(tài)角為0.15o，角速度為零。

仿真總時長：10 000 s。

仿真工況：1）t=0 s 時刻，模擬在軌正常穩(wěn)態(tài)運行，三軸姿態(tài)角由星敏感器測量解算得出；2）t=500 s 時刻，月球矢量進入YOZ面內(nèi)，開始執(zhí)行對月觀測任務，控制器切換至跟蹤控制律；3）t=6 620 s時刻，對月觀測任務結束，恢復在軌星敏+飛輪的長期穩(wěn)態(tài)對地定向控制。控制律中不含陀螺角速度，結果如圖6～圖11 所示。

圖6 參考姿態(tài)Fig.6 Reference attitude

圖7 衛(wèi)星姿態(tài)1Fig.7 Satellite attitude 1

圖8 衛(wèi)星角速度1Fig.8 Satellite angular velocity 1

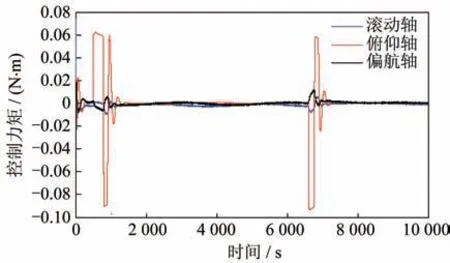
圖9 控制力矩1Fig.9 Control torque 1

圖10 跟蹤誤差1Fig.10 Tracking error 1

圖11 飛輪角動量1Fig.11 Flywheel angular momentum 1

控制律中含陀螺角速度，結果如圖12～圖16所示。

圖12 衛(wèi)星姿態(tài)2Fig.12 Satellite attitude 2

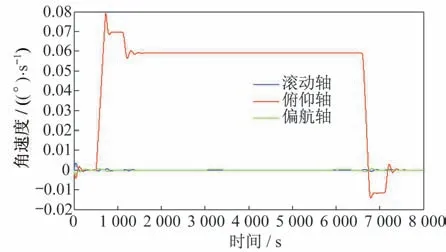
圖13 衛(wèi)星角速度2Fig.13 Satellite angular velocity 2

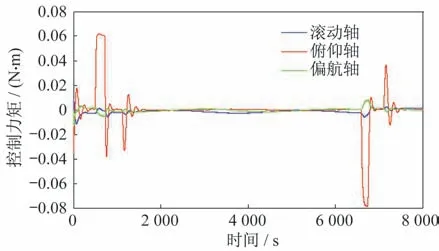
圖14 控制力矩2Fig.14 Control torque 2

圖15 跟蹤誤差2Fig.15 Tracking error 2

圖16 飛輪角動量2Fig.16 Flywheel angular momentum 2

從數(shù)值仿真結果得出以下結論：

1）由于穩(wěn)態(tài)和跟蹤控制律在控制誤差較小的情況下基本相同，該控制方案可以實現(xiàn)進入和退出對月觀測模式時姿態(tài)平穩(wěn)過渡，且任務過程中除了過渡部分外姿態(tài)控制精度可到達穩(wěn)態(tài)控制精度的要求，即小于0.15°。

2）使用一個偏置動量輪進行控制也可實現(xiàn)對月觀測，但由于單個動量輪僅能提供最大0.075 N·m的力矩，穩(wěn)態(tài)到對月以及對月到穩(wěn)態(tài)的過渡過程較長，且過渡部分姿態(tài)誤差較大。

3）軌道周期101 min，對月定標前到對月觀測的過渡時間為1 000 s，每軌實際用于對月定標的時間達83 min，滿足大于30 min 的需求。

4）有陀螺角速度信息的控制結果與無陀螺速度相比，角速度的超調(diào)更小，更有利于防止系統(tǒng)積分飽和導致控制發(fā)散。

5 結束語

機動對月定標模式是FY-3（05）衛(wèi)星首次引入的新工作模式，從載荷定標的角度，該模式能夠增加中分對月球的觀測時間，有利于提高定標數(shù)據(jù)的測量精度。但該工作模式對整星其他各分系統(tǒng)的狀態(tài)影響較大，會影響衛(wèi)星的業(yè)務運行，建議盡量采用每月一次的非機動對月定標，機動對月定標的實施頻次不宜過多，確有需要時，可1～2 a 開展一次。