基于IGMM-Copula的入庫徑流過程預報誤差隨機模擬模型

張驗科，張佳新，邰雨航，紀昌明，馬秋梅

（華北電力大學水利與水電工程學院，北京 102206）

1 研究背景

入庫徑流預報誤差是水文預報不確定性的一種表現，目前的研究一般將量化其隨機性作為研究重點，多采用參數估計［1-2］、非參數估計［3］、最大熵［4］等方法對其分布形式近似描述，取得了大量研究成果［5-9］。考慮到入庫徑流預報誤差往往包含多種統計特征，若采用單一分布，例如正態分布、tLocation-Scale 分布等對其進行擬合，某些情況下雖然可呈現出較好的擬合效果，但由于各分布函數有時在對稱性和尾部特征上的表現存在差異，并不能保證總可以找到一種分布形式剛好能夠達到預期的要求；同時，已有的研究成果多集中于單一變量或單一預見時刻的徑流預報誤差的量化分析［10-11］， 而對于多個變量或多個預見時刻的徑流過程預報誤差的分析相對較少。對于預報調度工作而言，前期的入庫徑流預報作業多在某一固定時刻以某一固定間隔對預見期內多個后續時刻的入庫流量進行預報［12］，而根據對應時刻的歷時實測入庫流量序列，即可分析得到相應的徑流過程預報誤差序列。這一預報誤差序列反映了整個調度期的預報不確定性，而僅對單一預見時刻的預報誤差進行研究，則忽略了調度期內不同預見時刻預報誤差間的關聯性。因此，需要在尋求單一預見時刻預報誤差分布的基礎上，綜合考慮分析不同預見時刻預報誤差之間的相關性，才能更為全面地揭示入庫徑流過程預報誤差的變化規律。

為解決上述入庫徑流預報誤差分布研究中存在的問題，紀昌明等［13］依據高斯混合模型（Gaussian Mixture Model，GMM）在密度函數估計中的高度自適應性，結合高維meta-student t Copula 函數在耦合多個類型邊緣分布上的優勢，建立了多個預見時刻入庫徑流預報誤差的GMM-Copula隨機模型，可實現對入庫徑流預報誤差序列的隨機模擬。在該項研究中，GMM-Copula模型是以單一預見時刻徑流預報誤差分布的擬合結果為基礎建立的多維徑流預報誤差聯合分布，在應用過程中仍存在兩個關鍵問題：（1）高斯分布混合個數的確定，這是一個權衡的過程，個數過少會影響擬合的精度，相反則會導致模型過于復雜不利于分析；（2）參數初始值的確定，由于采用的是EM（Expectation-Maximization al?gorithm，EM）法［14］求解模型擬合需要的參數，它是一類通過迭代進行極大似然估計的優化算法，需要對高斯混合模型的權重等參數進行初始化，不同的初始參數值會對迭代的結果造成較大的影響，從而決定最終的擬合精度。由于原GMM-Copula 模型對于擬合過程的兩個關鍵問題都未做細致的研究，各個預見時刻的徑流預報誤差的高斯分布混合個數以及初始參數值的確定存在較大的主觀性，難以保證擬合結果的精度，從而得到的模擬誤差序列也存在進一步優化的空間。

本文基于AIC（Akaike Information Criterion，AIC）與BIC（Bayesian Information Criterion，BIC）準則［15］選取最優高斯分布混合個數，同時引入數據挖掘中的K-means++算法確定高斯混合模型的初始參數值，對GMM-Copula 模型中的GMM 部分進行改進，以此建立基于IGMM-Copula（Improved Gauss?ian Mixture Model Copula）的入庫徑流過程預報誤差隨機模擬模型。以雅礱江流域錦屏一級水庫短期入庫徑流過程預報誤差分析為例，基于IGMM-Copula 模型，首先對預見時刻為6 h、12 h、18 h 和24 h的入庫徑流預報誤差分布進行擬合分析；其次，將擬合結果作為邊緣分布從而建立四維入庫徑流預報誤差的聯合分布，據此對誤差序列進行隨機模擬與統計分析，并與GMM-Copula模型得到的結果進行了對比，驗證模型的可行性與合理性。

2 GMM-Copula中高斯混合模型描述及其存在的問題

現假設預報誤差為ex(i)t(j)，表示當預報起始時刻為x(i)時，對未來t(j)時刻進行徑流預報所產生的預報誤差，其中i表示歷史預報的次數，i∈(1,2,…，n)；j表示預報的時刻數，j∈(1,2,…，m)。可定義為：

式中：Sx(i)t(j)、Hx(i)t(j)分別為預報流量值和實測流量值。

當進行n次預報后，可得到由n個預報誤差序列組成的誤差數據矩陣E：

針對時刻t(j)的預報誤差ex(i)t(j)，可利用高斯混合模型求其分布，設模型中待估計的參數為θ，則高斯混合模型的概率密度函數可表示為：

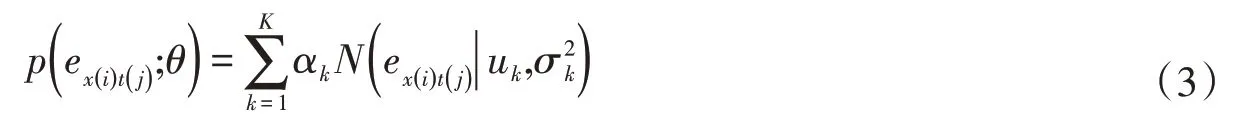
式中：p(ex(i)t(j);θ)為高斯混合分布的概率密度函數；αk、uk、σ2k分別為第k個高斯分布的參數，分別代表權重、均值和方差，且K表示高斯混合模型中的高斯混合個數。

從式（3）中可知，若要求解單一預見時刻誤差分布擬合的表達式，則需要對參數αk、uk、σ2k進行估計，而直接對原式進行最大似然估計則會產生對數的和，求解十分困難，因此采用EM法［14］對參數進行推求。具體的求解步驟如下。

（1）進行EM 算法中的E 步（求期望值），提出一個隱變量γik，γik∈{0,1}，表示第i個樣本是否來自于第k個高斯分布，k=1，…，K。將γik引入式（3），得到單個樣本完全數據的對數似然函數，如式（4）。對參數θ進行初始化，其中ak=1/K，uk設為隨機數，σ2k取1，根據利用貝葉斯定理求解γik的后驗概率P(γik=1|ex(i)t(j),θ)，見式（5）。

（2）進行EM 算法中的M 步（求最大值），由式（4）得到全部樣本完全數據的對數似然函數，見式（6）。依據式（6）分別對αk、uk、σ2k求偏導，令似然函數值為0，求出更新后的參數分別如式（7）所示。

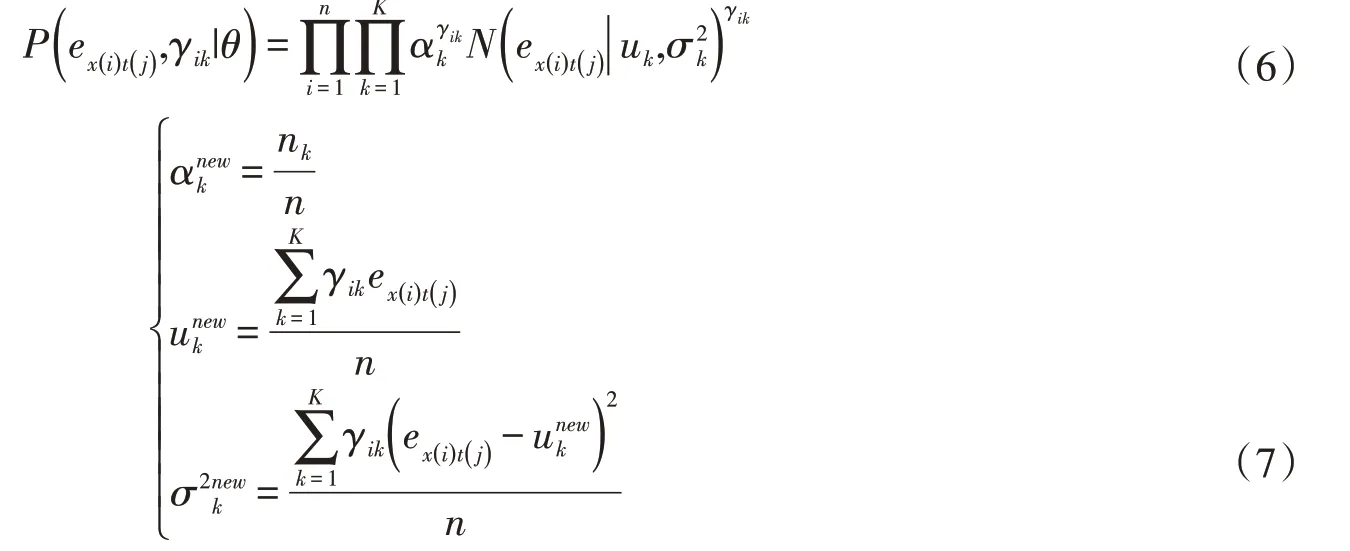
（3）不斷迭代步驟（1）和（2），重復更新αk、uk、σ2k，直到前后兩次迭代結果的變化幅度小于一個設定值ε，則終止迭代，即|θ-θnew|≤ε，θnew代表更新后的參數值，ε通常取10-4。

GMM-Copula 模型在對單一預見時刻誤差分布進行估計的過程中，由于涉及到高斯混合個數K的選取，而通過人為確定的常規方法主觀性太強，尤其在于相鄰時段的預報誤差分布可能具有不同的特征，若高斯混合個數選取不當，勢必會對最終擬合的精度造成影響；同時，模型采用隨機抽取確定初始參數值的方式同樣不嚴謹，初始值的不同會影響最終迭代得到的參數，從而影響最終分布擬合的結果。本文基于AIC與BIC準則選取最優的高斯混合個數，同時采用K-means++算法確定高斯混合模型參數的初始取值，建立基于IGMM-Copula 的入庫徑流過程預報誤差隨機模擬模型。模型在優化單一預見時刻徑流預報誤差分布擬合方法的基礎上，考慮了各個預見時刻之間的相關關系，并結合隨機抽樣理論，可實現對多個預見時刻入庫徑流過程誤差的隨機模擬。

3 基于IGMM-Copula的入庫徑流過程預報誤差隨機模擬模型

模型主要從兩個方面敘述，提出GMM-Copula 模型改進的兩個方面；2.3 節描述了如何利用IGMM-Copula模型建立多個預見時刻的徑流預報誤差聯合分布以及誤差序列隨機模擬的步驟。

3.1 基于AIC與BIC準則的最優高斯分布混合數選取AIC與BIC都作為衡量統計模型擬合優良性的標準，與AIC不同的是，BIC引入了與模型參數個數相關的懲罰項，考慮了樣本數量，更適合樣本數量較多時的情況。對應的計算公式如下：

式中：K為模型的參數個數，在本文中表示為高斯混合模型中的高斯混合個數；n為預報誤差樣本個數；L為模型參數求解中所對應的似然函數。

當模型的參數變動時，AIC 及BIC 的值越小則表示模型的擬合效果越好。由于高斯混合模型中K≥2，因此選擇以K=2作為起點，通過逐一列舉的方式計算模型擬合預報誤差分布的AIC 及BIC 的值，并選取對應AIC及BIC值最小的K值作為當前預見時刻誤差分布最優的高斯分布混合個數。

3.2 基于K-means++的參數初始值確定K-means++算法是一種確定聚類迭代初始起點的算法［16］，一般用于初始化K-means++聚類算法的聚類中心。高斯混合模型本質上作為一種聚類模型，其原理是通過計算每個數據所屬的高斯類從而實現聚類的效果，因此同樣可以利用K-means++算法進行預分類，并根據預分類的結果計算高斯混合模型的初始參數值，其具體步驟如下：

（1）從單一預見時刻誤差數據集中隨機選定與最優高斯分布混合數K相同數目的初始聚類中心；

（2）計算每個誤差數據ex(i)t(j)與之最近一個聚類中心的馬氏距離D(ex(i)t(j))；

（4）重復（2）（3），直至每一個聚類中心不再變化為止；

（5）依據得到的聚類中心將誤差數據聚類，并計算每個類的均值u′k與方差(σ2k)′作為迭代的初始值，其中權值的初始值

當初始參數值確定后，利用EM算法迭代計算則可得到最終的αk、uk、σ2k，帶入式（3）即可得到單一預見時刻的誤差分布表達式。

3.3 多個預見時刻徑流預報誤差聯合分布建立及應用meta-elliptic Copula 函數族中的高維meta-stu?dent t Copula［17］、高維meta-Gaussian Copula［18］是水文中常用的兩類分布，由于在預報模型在預報過程中受到的干擾因素難以量化，可能會在某一時間點產生與均值偏離較大的預報誤差，而高維meta-Gaussian Copula 不具有尾部相關性，因此本文在推求各個預見時刻誤差分布的前提下，選用高維me?ta-student t Copula建立多個預見時刻徑流預報誤差間的聯合分布，可表示為：

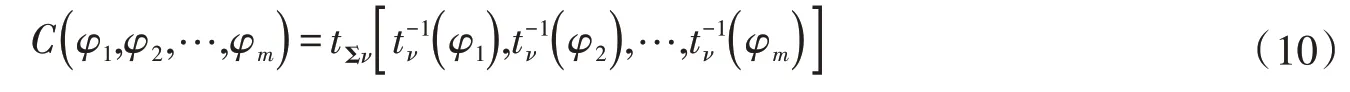
將其展開可得：

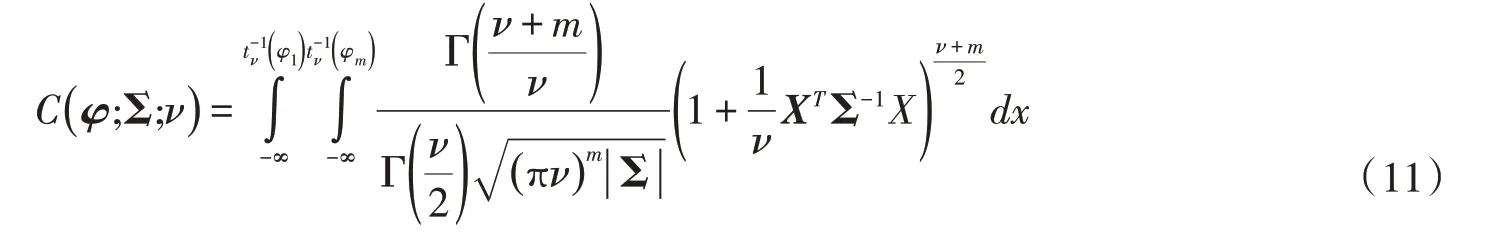
式中：C(φ1,φ2,…,φm) 為m維隨機變量聯合分布，φ1，φ2，…，φm分別表示m個預見時刻的入庫徑流預報誤差；tΣν為ν個自由度的t分布函數，其協方差矩陣為Σ；t-1ν(·)為自由度為ν的t分布的逆函數；Γ(·)為伽馬分布；X為不同預見時刻的預報誤差變量矩陣，X=(φx(i)t(1),φx(i)t(2),…，φx(i)t(m))；φ為被積函數變量矩陣，φ=[φ1,φ2,…，φm]T。

當對整個入庫徑流預報過程進行不確定性分析時，需要依據入庫徑流過程預報誤差聯合分布對誤差序列進行隨機抽樣，主要分為如下兩步。

（1）依據聯合分布C(φ1,φ2,…，φm)生成隨機序列矩陣ω=[ω1,ω2,…，ωm]，ωj表示對應預見時刻誤差分布的累積分布概率。

（2）推求對應預見時刻誤差分布的逆累積分布函數Fj-1(φi)，將隨機序列矩陣ω帶入該函數，可得到模擬的入庫徑流過程誤差序列，表示為e′=(F1-1(ω1) ,F2-1(ω2),…，Fm-1(ωm))。

基于IGMM-Copula的入庫徑流過程預報誤差隨機模擬模型的研究流程如圖1所示。

圖1 基于IGMM-Copula的入庫徑流過程預報誤差隨機模擬模型的流程

4 基于IGMM-Copula的入庫徑流過程預報誤差隨機模擬模型

錦屏一級水電站水庫在雅礱江下游“錦官電源組（錦屏一級、錦屏二級、官地）”梯級水電站水庫群中起控制性作用，其入庫徑流預報采用的是三水源新安江模型［19］，具體是以每天早上的8 點作為預報起點，以連續預報的形式對當天14點、20點、次日2點及次日的8點進行徑流預報（依次對應預見時刻為6 h、12 h、18 h和24 h），一次預報可得到未來一天的預報流量序列，以此制訂水電站水庫的調度計劃［20-21］，預報的實施過程見圖2。自投產以來，存在因來水預測誤差造成水庫運行水位超出控制范圍而需要調整發電計劃的情況［22］，本文選用錦屏一級水電站水庫2014年1月1日至2017年9月23日每日的實測及預報徑流資料，根據式（1）計算得到未來24 h 內的預報誤差序列（每個序列包含4 個預見時刻的預報誤差），共得到1362 條預報誤差序列樣本，而后利用本文所提方法建立基于IGMM-Copula 的入庫徑流誤差隨機模擬模型，一方面通過求解各預見時刻的徑流預報誤差分布，分析了確定性預報模型產生預報誤差的統計特征和分布規律，同時也考慮了不同預見時刻下預報誤差的相關性，實現了對預報誤差的多元聯合模擬，為根據預報資料制訂水庫調度計劃，提供了更多參考信息。

圖2 錦屏一級水電站水庫徑流預報實施過程

4.1 各預見時刻徑流預報誤差分布求解基于IGMM-Copula模型中的分布擬合部分（此處稱為IGMM）對各預見時刻徑流預報誤差經驗分布進行擬合，首先需要確定各時刻預報誤差的最優高斯混合數，在原GMM 模型中，由于沒有相應的指標作為參考，作者偏向于參數較少，更容易求解的模型結構，因此最終選取的高斯混合數為K=2。現以K=2 為起點，根據逐一列舉法計算不同K值下的AIC 及BIC的值。其計算結果如表1。

從表1可以看出，以6 h、12 h、18 h、24 h 徑流預報誤差為基礎建立的IGMM 在AIC 及BIC 的值取得最小時，對應的最優高斯混合數為K=3，據此可建立對應權重的IGMM 對各預見時刻徑流預報誤差進行擬合，表2為基于IGMM 的各預見時刻徑流誤差分布參數估計值。為體現IGMM 在誤差分布估計方面的優勢，將原GMM 與單高斯分布（SGM）作為比較模型。其中，GMM 高斯混合個數的選取及參數初始值的確定均按照原文獻里介紹的方法進行計算。

表1 不同高斯混合數下各預見時刻徑流預報誤差IGMM的AIC及BIC的值

表2 基于IGMM的各預見時刻徑流誤差分布參數估計值

圖3是3 種模型對不同預見時刻徑流預報誤差的擬合效果圖，其中實測預報誤差樣本個數n≥1000，據此做出的頻率直方圖總體呈現出對稱的形狀，誤差數據大部分集中在0值附近，SGM 擬合得到的概率密度函數較為矮胖，在峰部的集中度與頻率直方圖相差較遠，而IGMM 與GMM 由于自適應性較強，兩者的擬合結果在數據集中的位置更契合頻率直方圖，在圖中體現為概率密度函數的形狀更為尖瘦，因此能更大程度的反映實測預報誤差樣本所展現的規律，這也印證了高斯混合模型在概率密度估計中的優越性。同時，由于不同預見時刻的徑流預報誤差具有不同的特征，而人為確定GMM 中高斯混合數與參數初始值難以達到最佳的擬合效果，尤其對于預報誤差數據峰部的擬合，基于IGMM 得到的擬合曲線的擬合效果明顯優于GMM，其原因主要在于IGMM 對高斯混合數進行了優選，并對參數初始值進行了預計算，因此擬合曲線更貼近于頻率直方圖。

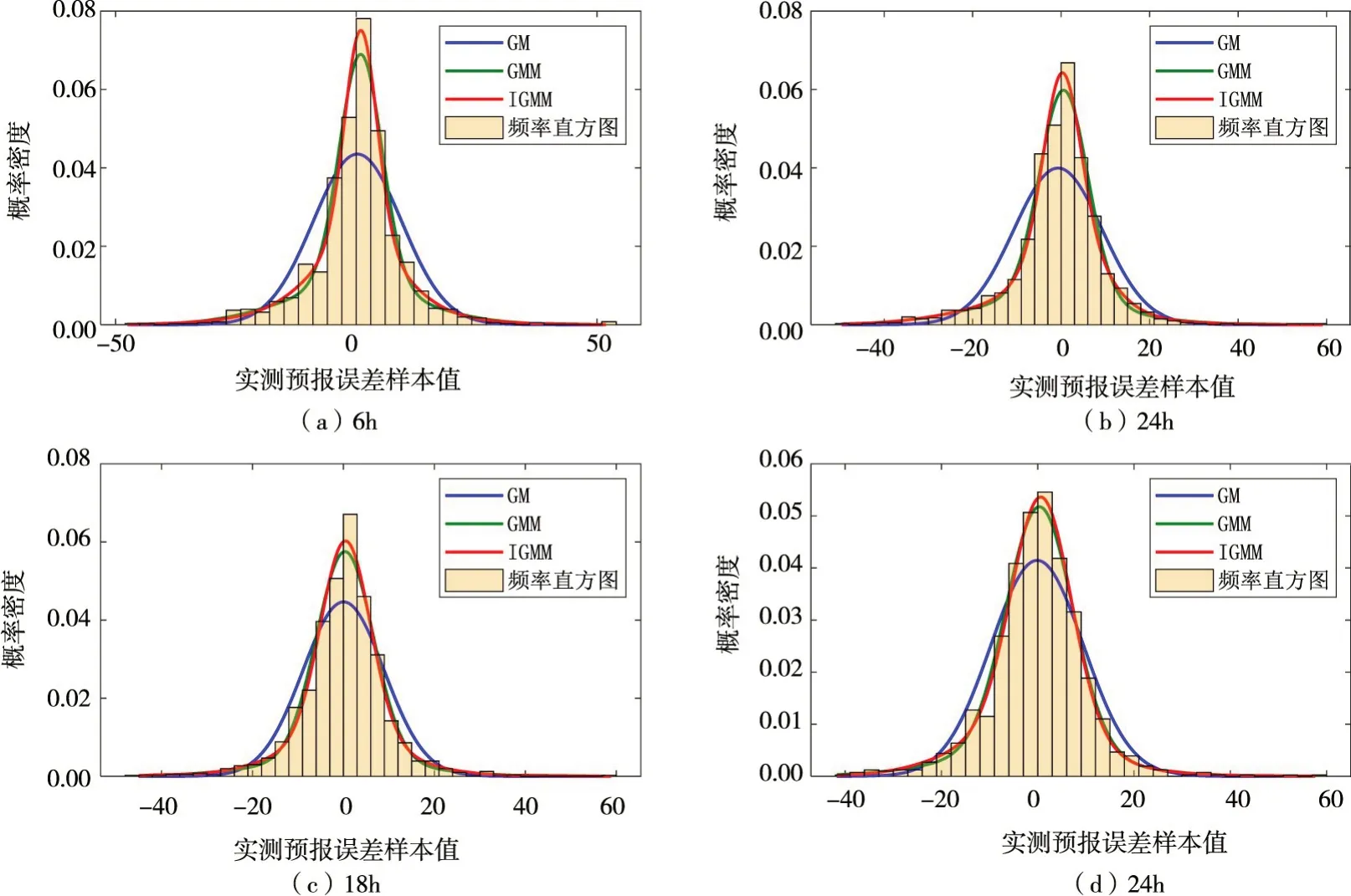
圖3 三種模型對不同預見時刻徑流預報誤差的擬合效果

4.2 模型適用性檢驗適用性檢驗包括擬合優度檢驗與后驗檢驗，擬合優度檢驗的目的是用歷史數據來檢驗模型是否能夠反映徑流誤差的隨機特性［23］，具體包括χ2檢驗、t-檢驗、K-S 檢驗等，其中K-S 檢驗是一種檢驗單個總體是否服從某一理論分布的非參數檢驗方法，相比于χ2檢驗能夠更充分地利用樣本信息，適用于連續和定量數據［24］。K-S檢驗統計量Dn定義見下式：

式中：Dn越小說明擬合優度越高；Fn(·)為經驗分布函數；Ft(·)為假設的理論分布函數。分別對改進高斯混合模型、核密度估計模型以及單高斯模型進行K-S 檢驗，顯著性水平設置為0.01，其計算結果見表3。

從表3可看出，IGMM 及GMM 都通過K-S 檢驗，即兩者與經驗分布在顯著性水平為0.01 的前提下沒有顯著性差異，驗證了IGMM 與GMM 模型在徑流預報誤差密度估計中的可行性，同時IGMM 在各預見時刻下誤差擬合曲線的Dn值都為最小，說明其對于單一預見時刻徑流預報誤差經驗分布的擬合優度最高。

表3 模型K-S檢驗指標值

后驗檢驗的目的是定量評估概率模型與數據觀測分布（即統計直方圖）之間的差異［25］，采用式（13）的均方根誤差εRMSE與式（14）的平均誤差百分數εMAPE作為指標對求得的各預見時刻徑流誤差分布進行檢驗，得到的指標越小，說明擬合模型與數據觀測分布之間的差異越小，其計算結果見表4。

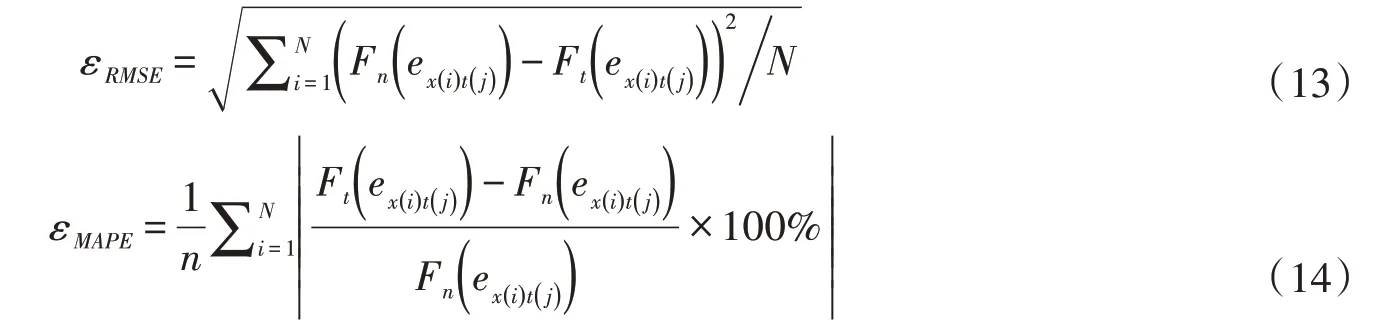
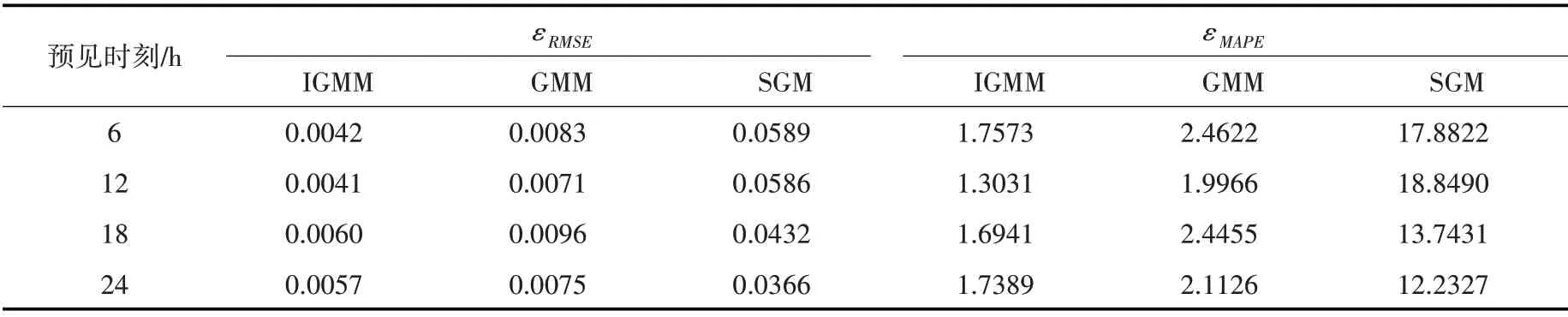
表4 模型后驗檢驗指標值

由表4可見，對于所有預見時刻而言，基于IGMM 得到的誤差分布的εRMSE都保持在0.06 及以下，εMAPE都保持在1.8 以下，相較于SGM 與GMM，在兩指標上的表現最好，說明基于IGMM 得到的各預見時刻誤差分布與數據觀測分布之間的差異相差最小。

為分析不同預見時刻間徑流預報誤差分布的差異，圖4將IGMM 擬合得到的各徑流預報誤差分布曲線匯總，從圖中可觀察到，隨著預見時刻的增加，誤差分布形狀逐漸從“尖瘦型”變化為“矮胖型”，表面預報不確定在隨時間的增加而增大，符合確定性預報模型的預報規律。

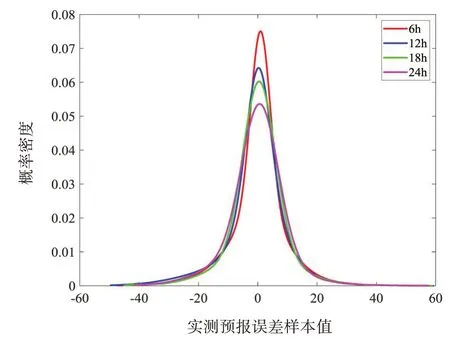
圖4 各預見時刻徑流預報誤差分布曲線

4.3 徑流預報誤差序列隨機模擬首先分析預見期內各時刻徑流預報誤差兩兩間的相關性，et(6)、et(12)、et(18)、et(24)分別表示6 h、12 h、18 h、24 h 的徑流預報誤差，采用Kendall 相關系數作為相關性的度量并進行雙側顯著性檢驗，設置零假設為：變量et(6)、et(12)、et(18)、et(24)沒有相關性，顯著性水平為0.05，其計算及檢驗結果如表5所示。

從表5可知，雙側假設檢驗的P 值均小于顯著性水平，因此拒絕零假設，認為各預見時刻的預報誤差均存在正相關性，考慮利用高維t-Copula建立徑流過程預報誤差的聯合分布并據此進行誤差序列抽樣，實現對預報誤差序列的隨機模擬。

表5 各預見時刻徑流預報誤差間的Kendall相關系數

為檢驗高維t-Copula 對多維誤差的適用情況，根據圖形分析法原理，以IGMM 求得的6 h、12 h、18 h、24 h徑流預報誤差分布為例，分別按式（11）與式（15）計算誤差的理論聯合分布概率和經驗聯合分布概率，并點繪兩者的關系圖，見圖5。

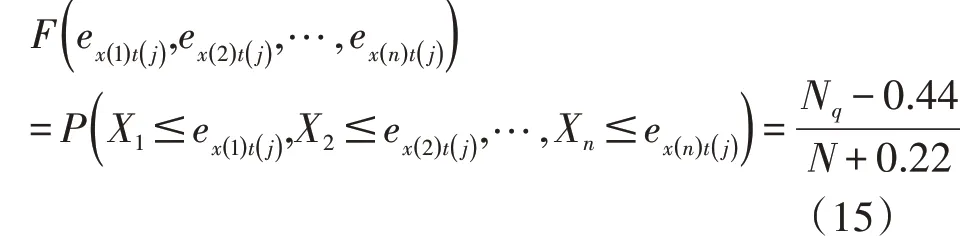
圖5 理論聯合分布概率與經驗聯合分布概率關系

式中：Nq為同時滿足X1≤ex(1)t(j)，X2≤ex(2)t(j)，…，Xn≤ex(n)t(j)的樣本個數；N為樣本總量。

其中，由于實測預報誤差樣本個數較大，因此繪出的散點圖比較密集（圖5中藍色數據點），形狀趨向于一條線，由趨勢線的斜率可看出，圖中的點都大致落在45°對角線兩側，理論聯合分布概率和經驗聯合分布概率的RMSE為0.00907，表明利用高維t-Copula建立多個預見時刻徑流預報誤差的聯合分布是合理可行的。

現根據IGMM 求出的各預見時刻徑流預報誤差分布為邊緣分布，以高維t-Copula 作為連接函數，建立基于IGMM-Copula 的入庫徑流過程預報誤差隨機模擬模型，并與GMM-Copula 模型進行對比，按照2.3 節的步驟分別利用兩模型對預報誤差序列進行500 000 次隨機模擬，計算IGMM-Copula 與GMM-Copula模擬預報誤差的統計參數，計算結果見表6和表7。

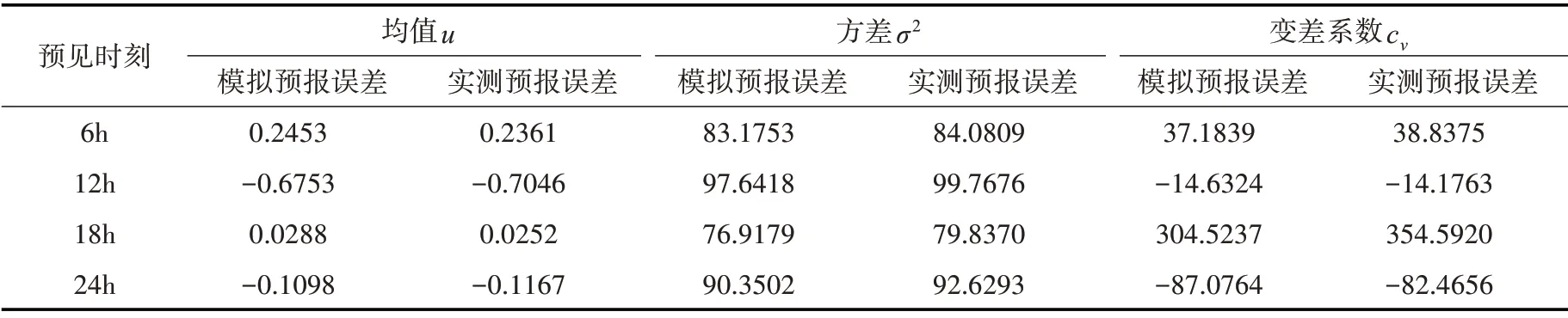
表6 GMM-Copula模擬預報誤差與實測預報誤差的統計參數值

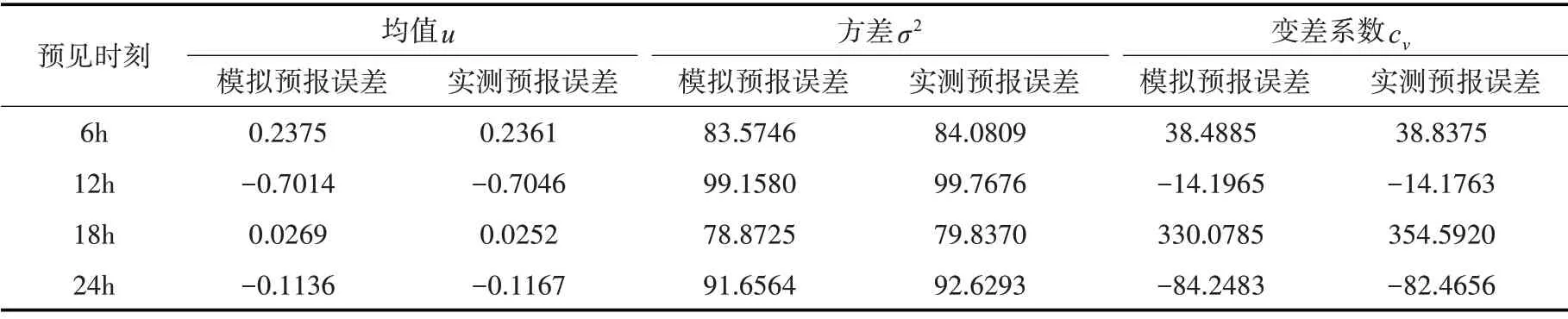
表7 IGMM-Copula模擬預報誤差與實測預報誤差的統計參數值

由表中可知，相較于GMM-Copula模型，IGMM-Copula模型各預見時刻模擬預報誤差的統計參數更貼近于實測預報誤差，而在18 h 時，由于誤差均值較小，模型模擬預報誤差與實測預報誤差的變差系數產生了較大的差異，而IGMM-Copula 模型明顯更優于GMM-Copula 模型，這也反應了不同的預報誤差邊緣分布會對抽樣結果造成一定程度的影響。從統計參數的整體變化趨勢分析，IGMM-Copula 模型的模擬預報誤差能與實測預報誤差保持一致，說明模型能夠很好的反映徑流預報誤差序列的統計特性，可作為對預報結果進行修正的參考依據。

5 結論

本文在GMM-Copula 模型的基礎上，對高斯混合數的選取以及初始參數值的確定進行了改進，建立了基于IGMM-Copula 的入庫徑流過程預報誤差隨機模擬模型，模型可運用于單個預見時刻及多個預見時刻的徑流預報誤差分析與模擬。以錦屏一級水庫為例的結果表明：對于單一預見時刻的徑流預報誤差的描述，IGMM-Copula 模型在擬合優度檢驗及后驗檢驗中皆優于單高斯與GMMCopula 模型；通過IGMM-Copula 模型模擬得到的誤差序列的均值、方差和變差系數相較于GMMCopula 模型更貼近于實測誤差序列，統計參數的變化規律基本一致，驗證了模型的可行性，不僅為研究徑流預報誤差提供一種新的方法，也為水庫短期優化調度計劃的制訂提供了更為豐富的參考信息。