可變勾股模糊VIKOR水資源系統韌性評價調控模型及應用

楊亞鋒，王紅瑞，鞏書鑫，鄧彩云

（1.北京師范大學 水科學研究院 城市水循環與海綿城市技術北京市重點實驗室，北京 100875；2.華北理工大學 理學院，河北 唐山 063000）

1 研究背景

水資源是人類賴以生存和發展的基礎，各種水問題頻發促使人類思考更合理的水資源可持續利用策略［1-4］。作為研究熱點之一，安全評價與風險管理是實現水資源系統可持續發展的重要途徑［5-6］。近年來，韌性理念逐漸在城市水資源系統的研究中受到關注［7-9］。

韌性（Resilience）一詞源自拉丁語中的“Resilio”，是“復位到原始狀態”的意思。與風險分析相比，韌性研究更強調系統本體具備的應對外來沖擊的能力。不同學者對水資源系統韌性有著不同理解：我國學者俞孔堅等［10］提出了水系統韌性的概念，認為水系統具備韌性的特征。Alessa 等［11］在已有水資源評價指數的基礎上建立了水資源脆弱性指數，用以表達水資源系統韌性。Sandoval-Solis 等［12］以“赤字”為衡量值，從可靠性、恢復性和脆弱性三個方面建立了水資源可持續性指標。Yang 等［13］以尼泊爾河流域為研究對象，結合Sandoval-Solis 等的“赤字”概念，從穩定性、恢復性和脆弱性三個方面衡量水資源的可持續性。Huang 等［14］利用GIS 和ABM 模型對城市水系統韌性開展研究。在以上研究的基礎上，作者認為水資源系統韌性指水資源系統及其基本功能在受到自然或人類活動干擾時，具備恢復原有水資源系統功能，并達到新的適應平衡的特性，這個恢復包含了自然和人工的調控作用。

水資源系統是一個復雜多因素系統，與經濟、社會和生態環境等多個系統之間存在密切的耦合關系，其韌性評價必然面臨多準則決策（Multiple-Criteria Decision Making，MCDM）問題［15］。多準則決策是指在具有相互沖突、不可公度性（Non-commensurable）的方案集中進行選擇的決策，其主要目標是在考慮多個屬性的情況下，選擇最優方案或進行方案排序。綜合考慮水資源系統的影響因素，對其韌性水平進行時空排序，進而分析其演化規律，開展水資源系統韌性的評價與調控，對于水資源系統的安全維護和可持續發展策略的制定具有重要的指導意義。

勾股模糊集方法是多準則決策過程中決策矩陣的重要獲取途徑之一。Yager等［16-17］研究了勾股模糊數（Pythagorean Fuzzy Numbers，PFNs）和復數之間的聯系，討論了一種決策方法，隨后定義勾股聚類算子，并應用于新的MCDM 問題處理技術之中［18］。Zhang 等［19-20］提出了基于備擇方案與理想解的相似性度量的PF（Pythagorean Fuzzy，PF）-MCDM 決策方法。Ma 等［21］構建了對稱勾股模糊算子并應用于MCDM 問題中。Ren 等［22］開發了勾股模糊集用于交互式多準則決策的方法；李德清等［23］基于距離測度，結合排序函數構建了一種勾股模糊集多屬性決策模型。

近年來，將勾股模糊集與VIKOR（Vlsekriterijumska Optimizacija I KOmpromisno Resenje，VIKOR）方法融合，結合正負理想點和距離測度進行排序與決策是一個前沿的研究方向。如：Muhammet Gul等［24］以礦山安全風險評價為例，將勾股模糊VIKOR 方法應用于職業風險評價，融合考慮職業健康安全專家在主觀判斷過程中感知的不確定性和模糊性，提出一種新的職業健康安全風險評估方法來確定風險等級；Liang 等［25］在傳統VIKOR 方法的基礎上，通過引入TODIM（an acronym in Portuguese for Interactive Multi-criteria Decision Making，TODIM）處理決策者的心理行為，定義勾股模糊熵和交叉熵測度，提出了一種折衷解決方案的新視角，并應用于加納銀行業網上銀行網站質量的評價；Pratibha R 等［26］基于勾股模糊熵和散度將勾股模糊集VIKOR 方法應用于印度可再生能源技術的評價之中，等等。可見，勾股模糊集與VIKOR 方法的融合，已經在諸多領域取得了成功應用，但在以往研究中，勾股模糊決策數往往依據專家經驗進而通過語言量表對應獲得，相鄰等級之間具有絕對分明的邊界。而事實上，特定指標下某一待評對象的狀態，往往在兩個相鄰等級之間模糊存在；若絕對地將其歸為某一等級，則均會損失一定的客觀性。以水資源系統韌性為例，若某一指標的值處在［20，30］為一級，對應勾股模糊數為［0.85，0.15］；處在［30，40］為二級，對應勾股模糊數為［0.75，0.25］，那么如果某一待評對象的該指標值為30，則需考慮如何確定其勾股模糊數。根據可變集相對隸屬度的方法，該待評對象對于該指標應該在一級和二級之間對立統一，這符合人們的思維認知。

基于此，首先采用可變集相對隸屬度的方法獲取勾股模糊決策矩陣，構建一種可變勾股模糊VIKOR 多準則評價模型；其次從韌性視角出發，構建指標體系與等級標準，進一步將模型應用于長江經濟帶的水資源系統韌性評價，給出調控策略，為該區域的水資源安全和可持續發展提供支持。

2 主要方法

水資源系統是一個復雜系統，其韌性水平及影響因子往往具有模糊不確定性。模糊隸屬函數是解決該類問題的有效手段之一。然而，由于水資源系統和人類思維的復雜性，傳統的隸屬度已不能滿足實際決策需求。勾股模糊集、可變模糊集等幾種新的工具應運而生。本文主要利用可變集中相對隸屬度方法對勾股模糊集進行改進，進而與VIKOR多目標決策方法進行融合拓展研究。

2.1 勾股模糊集勾股模糊集（Pythagorean Fuzzy Sets，PFSs）放寬了直覺模糊集理論中隸屬度與非隸屬度之和小于等于1 這一條件，約定隸屬度與非隸屬度之和可以超過1，但其平方和不超過1。勾股模糊集中的隸屬度和非隸屬度對應勾股定理中的兩個勾股數，故Yager 形象地稱其為勾股模糊集［16］。對于水資源系統的抵抗性、恢復性和適應性水平，從隸屬度和非隸屬度兩方面綜合表達更符合人們的思維認知。

設論域X上的一個勾股模糊集PFSs指的是如下形式的一個集合：

其中uP:X→[0,1]，vP:X→[0,1]。若滿足對于任意xi∈X，(uP(xi))2+(vP(xi))2≤1，則分別稱uP和vP為xi對P的隸屬度和非隸屬度，稱為xi對P的猶豫度或不確定度。

若將隸屬度uP（xi）和非隸屬度vP（xi）看作二維直角坐標系中橫坐標軸和縱坐標軸上的向量，則視為隸屬度與非隸屬度向量的模，稱為勾股模糊集P的自信度；自信度的作用效果與rP(xi)和uP(xi)所在方向的夾角有關。

設rP(xi)和uP(xi)所在方向的夾角為θP(xi)，Yager 定義了一個刻畫自信度rP(xi)方向的量dP(xi)，稱為自信度的方向［16］。 其中，dP(xi)∈[0,1]， 且vP(xi)=rP(xi)sin(θP(xi))。

Zhang 等［19］記p=（up，vp），稱其為勾股模糊數（PFNs）。相應地稱為p的自信度；為p的猶豫度。

2.2 勾股模糊熵與散度水資源系統是一個多因子耦合系統。確定各因子的權重，對于評價與調控至關重要。熵和散度是勾股模糊集理論中的重要概念，也是權重確定的主要工具。Pratibha-Rani等［26］在直覺模糊熵的基礎上定義了勾股模糊集的PF 熵和PF 散度。在PF 熵和PF 散度的基礎上給出勾股模糊數（PFNs）的熵和散度。

設勾股模糊數p=（up，vp），則其PF-熵為

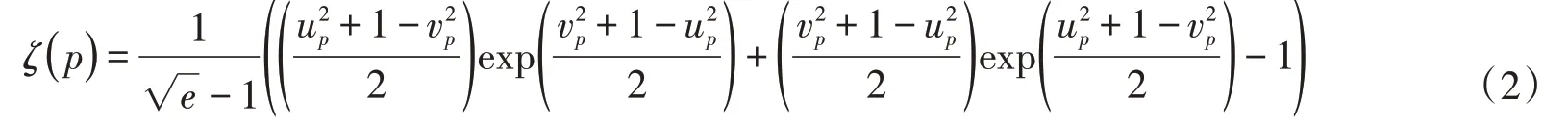
當up+vp=1時，上式可簡化為

設有勾股模糊數p=（up，vp），t=（ut，vt），其散度可表示為

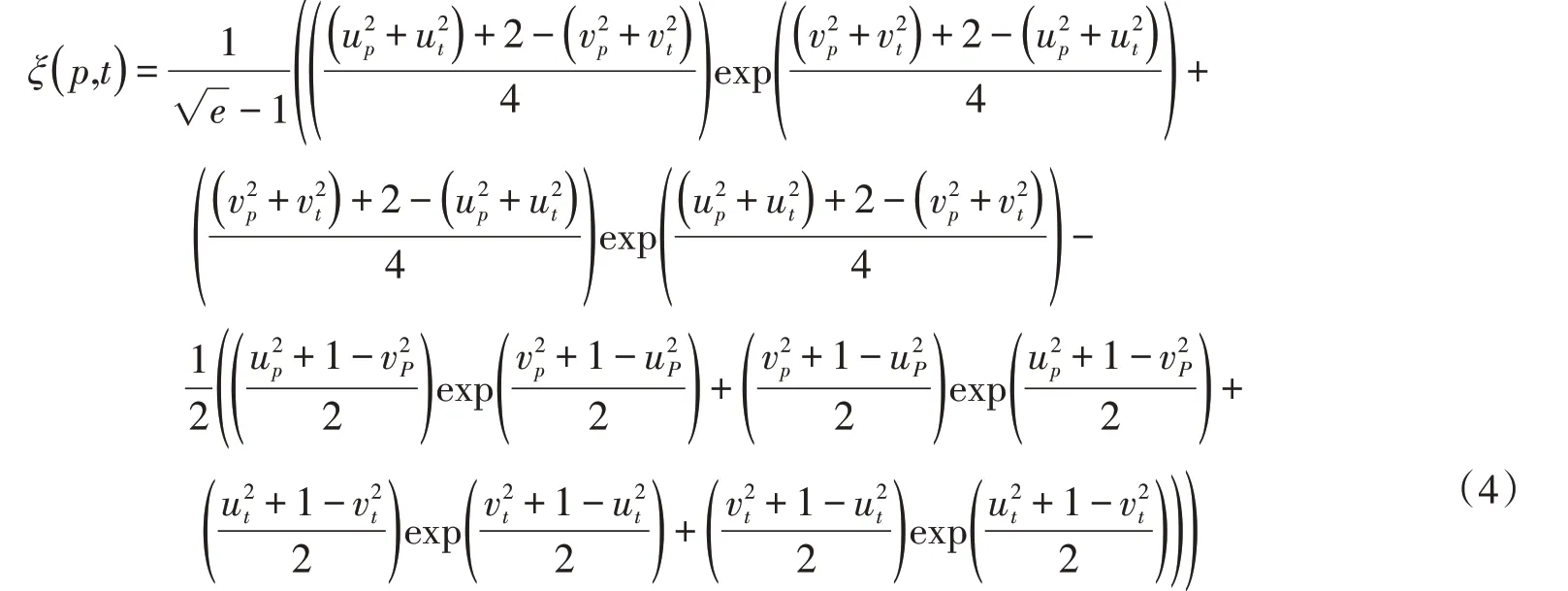
當uP+vP=1時，上式可簡化為

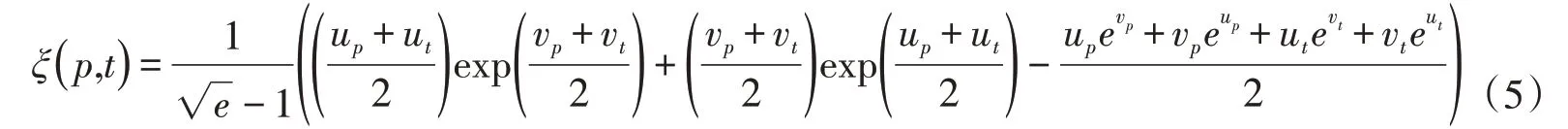
2.3 可變集與相對隸屬函數由于水資源系統韌性相鄰等級之間沒有明確的邊界，評價對象關于某個指標的等級也具有模糊性，應該介于兩個相鄰等級之間，且滿足對立統一性。陳守煜先生［27］于2005年提出的可變集方法是解決此類問題的有效手段。

可變集方法針對經典集合和模糊集合只研究靜態事物、現象與概念的問題，考慮事物變化過程中呈現出“非此即彼”的清晰性與“亦此亦彼”的模糊性兩者辯證對立統一的特性，提出了動態相對隸屬度概念，是對模糊隸屬度的一種拓展研究，已在水資源系統分析研究中得到了成功應用［27-29］。

可變集針對研究對象的對立清晰屬性進行研究，在向對立面轉化過程中，其隸屬程度可用對立測度值來衡量，它們隨時空條件的變化而變化，但其對立測度值之和恒為1。

設O為評價對象集合，o∈O，o的對立清晰屬性記以A與Ac。映射

稱為o對A與Ac的動態對立相對隸屬函數。

設評價對象集為O={oi} (i=1,2,…,m)，Xij=(xij)為對象oi的各指標cj(j=1,2,…,n)的值。指標cj分為s個等級，s個等級的指標值區間矩陣為：

其中ajh、bjh為指標cj在h級別標準值區間的上下限。

根據可變集對立統一定理，在級別h值區間中必定存在指標cj的級別h與級別h+1 的漸變式質變點kjh，質變點兩側對應兩級別相互對立。

由式（8）與矩陣I得矩陣K，K=[kjh，bjh]，若指標值xij在矩陣K相鄰兩級h與h+1區間，則xij對h級的相對隸屬度計算方法如下：

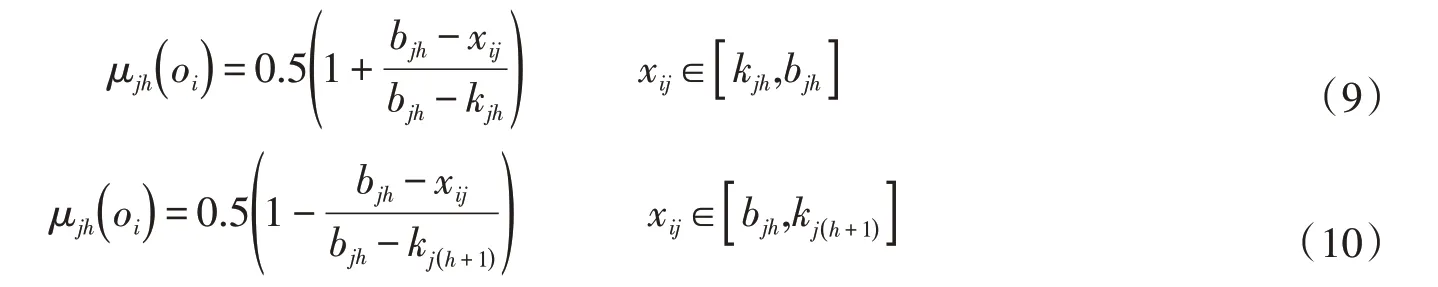
對于小于h級，大于h+1級的指標cj的相對隸屬度均為0，即：μj(h+1)(oi)=0。

2.4 VIKOR方法水資源系統韌性評價是一個多準則多目標的復雜決策問題。在獲取各研究對象關于各指標的勾股模糊隸屬度之后，需要綜合考慮各指標之間的序關系及相互作用。作為多準則決策MCDM 的重要方法之一，VIKOR 方法于1998年由Opricovic 首次提出，其主要目的是根據Lq-度量挖掘出一個折衷解決方案，使其在排序過程中更加接近理想解［30-31］。根據散度的定義，評價對象oi(i=1,2,…,m)的Lq-度量公式為

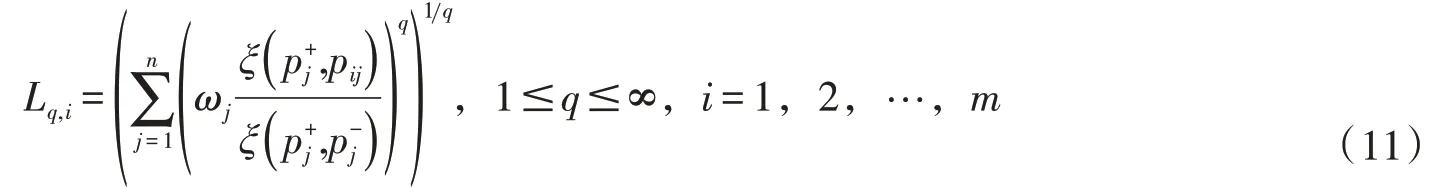
其中，ωj(j=1,2,…,n)是各指標對應的權重。和是第j個指標的正理想解和負理想解。Lq，i代表評價對象oi和理想解之間的距離。這種方法提供的折衷解決方案，滿足最大群體效益和最小個體遺憾，其度量分別為L1，i和L∞，i。

3 可變勾股模糊VIKOR水資源系統韌性評價調控模型設計

水資源系統韌性評價是個多指標決策過程，實施態勢評價與演化分析是韌性調控的前提。本文構建的模型算法設計如下：設有m個研究對象，記作o1，o2，…，om。評價與調控指標體系包含n個指標c1，c2，…，cn。對每個研究對象進行評判，進而所有對象進行優選排序；在評價排序的基礎上，結合實際情況提出調控策略。下面給出基于可變勾股模糊VIKOR多指標評價的具體步驟。

步驟1。勾股模糊決策矩陣。在實際應用中，一個關鍵的問題是合理估計PF 集的隸屬函數。目前，通過語言評分系統構建PF 數據的是普遍采用的一種勾股模糊的獲取方法。結合對水資源系統韌性評價調控認知，這里采用五點語言評價量表及其對應的PF值［32］。見表1。

表1 勾股模糊語言變量與勾股模糊數、韌性等級的對應關系

根據研究對象的實際指標值，利用可變集方法計算關于5個等級的相對隸屬度；若研究對象oi關于各個指標cj的相對隸屬度為μjh(oi)和μjh+1(oi)，則其oi關于指標cj的勾股模糊隸屬度期望值為pij=μjh(oi)ph+μjh+1(oi)ph+1，記作pij=。

步驟2。基于PF 熵和散度確定權重。設各指標的權重為ω1，ω1，…，ωn，且滿足條件0≤ωj≤1，且基于PF熵式（3）和PF散度式（5）的指標權重計算公式［26］如下：

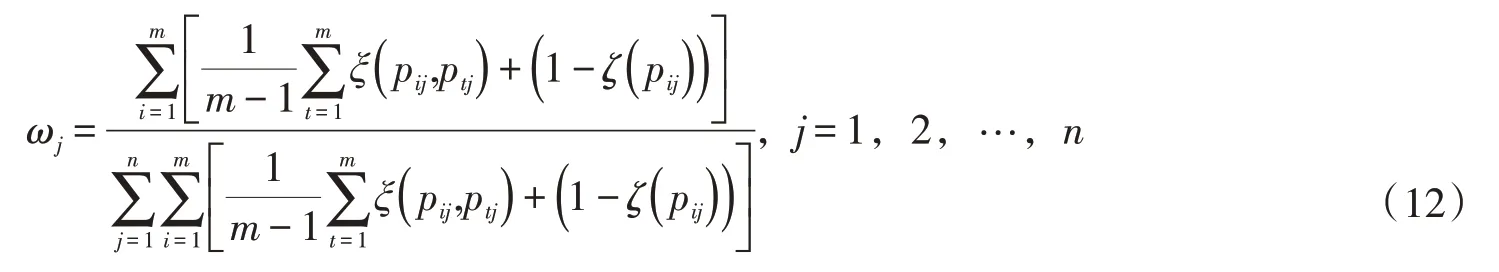
步驟3。確定正負理想點。比較所有研究對象o1，o2，…，om關于同一指標cj()j=1，2，…，n的勾股模糊數值pij=(i=1,2,…，m)，確定指標cj下的最優值和最劣值進而得到正理想指標值向量p+={p+1,p+2,…，p+n} 和負理想指標值向量

步驟4。計算利益比率。計算每個評價對象oi（i=1，2，…，m）的最大群體效益值Si、最小個體遺憾值Ii和利益比率值Qi，如下：

其中，S+=maxSi，S-=minSi，I+=maxIi，I-=minIi，τ∈[0,1]為決策系數。

步驟5。韌性水平排序。令Ri=1-Qi，稱為韌性排序值，則有：Ri越大，韌性水平越高。

步驟6。調控指標挖掘。針對指標cj(j=1，2，…，n)分別重復步驟4—5。對象oi()i=1,2,…,m的排序值記為Rij。設定閾值θ，進行異常檢測。若Rij<θ，則oi在cj下被判定為“劣”，否則為“優”。在指標cj下，若研究對象被判定為“劣”的個數則cj異常，為重點調控指標。

本文構建的水資源系統韌性評價模型流程圖，見圖1。

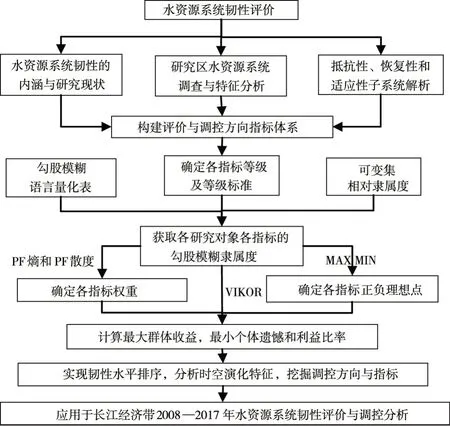
圖1 算法流程圖

4 實例分析

4.1 研究區選擇及數據來源長江經濟帶是指沿長江附近的經濟圈，東起上海，西到云南，幅員遼闊，覆蓋上海、江蘇、浙江、安徽、江西、湖北、湖南、重慶、貴州、四川、云南等11 個省市，面積約205.23 萬km2，占全國的21.4%，人口和生產總值均超過全國的40%。近年來受人類活動和氣候變化等影響，長江水環境惡化、水生態脆弱、水資源短缺與水旱災害等問題日趨嚴重。因此，開展該區域水資源系統的韌性研究，制定相應的調控策略對長江經濟帶水資源可持續利用、生態優先與綠色發展可持續戰略的實施有重要的意義。

本文所有數據均來源于上海等11 個省級行政區的地方統計年鑒（2009—2018年）、地方水資源公報（2009—2018年）以及中國統計年鑒（2009—2018年）。

4.2 指標體系構建韌性可以看作系統提升適應性并不斷適應風險與擾動的這一循環過程。在這一過程中，系統經歷了從風險沖擊到沖擊后維持自身穩定再到迅速恢復，甚至將危機轉變為機遇，實現創新發展等的不同階段。基于該理念，本研究結合以往水資源或水系統韌性研究［10］，將水資源韌性分為擾動前、擾動中和擾動后三個子過程，分別對應抵抗性、恢復性和適應性三個目標。水資源系統的韌性過程就可分解為：（1）受到干擾前，水資源系統能夠抵御干擾的能力；（2）受到干擾時，水資源系統恢復快慢的反應能力；（3）受到干擾后，系統能夠在此次干擾中習得的適應能力。

考慮水資源系統面臨壓力的多元性、復合性與吸收擾動的能力。水資源系統韌性取決于生態環境、地區空間結構、經濟社會、人口以及管理制度等各子系統間的相互作用，從抵抗性、恢復性和適應性三個方面，結合科學性、合理性以及可獲取性的原則來確定相應指標。

（1）抵抗性指標。抵抗性指標是指水資源系統在受到沖擊時，能夠抵御沖擊的能力。在水資源系統中，其面臨的潛在風險越大，受到的干擾就會越多，其抵抗性也就會相應越弱。當區域內洪澇、干旱等外生性因素越多，水資源系統遭受的沖擊就會越大，系統抵抗風險的能力越弱，韌性在抵抗性過程中的表現就會越差。相應地，當區域內水資源壓力、人口壓力等內生性因素同樣會導致水資源系統遭受巨大沖擊，導致抵抗風險能力變弱。

（2）恢復性指標。恢復性指標是指水資源系統受到沖擊后，恢復至受沖擊前狀態的能力。在水資源系統中，恢復的過程受到水環境、經濟以及用水結構等內部因素影響，區域內部因素決定了系統恢復過程的快慢。從影響恢復性的主體看，可以分為環境、生態、經濟、社會等幾個方面：例如，污水的處理決定了水環境的承載能力；經濟結構影響用水結構，經濟發展水平影響用水效率，而農業、工業用水則遠大于第三產業用水；不同的用水效率、能耗效率也會影響水資源的韌性水平等。

（3）適應性指標。適應性指標是指在水資源系統在受到沖擊并恢復后，能夠在其中學習到的適應能力。水資源系統的適應過程，主要受到區域內的創新因素、保障因素等影響。不同的適應水平決定了系統在下一次受沖擊時，能夠遷移到的新的初始狀態水平。在水資源系統中，對適應性的影響主要集中在區域可持續發展以及水資源可持續利用等方面。

根據以上指標體系構建原則及范圍，構建水資源系統韌性評價指標體系。參考相關文獻及行業標準［33-36］，結合長江經濟帶實際情況，制定等級標準。具體見表2。

表2 長江經濟帶水資源系統韌性評價指標體系及等級標準

4.3 模型實施基于以上數據和標準，利用構建的韌性評價模型對長江經濟帶2008—2017年水資源系統韌性的時空演化過程與調控策略展開研究，具體步驟如下：

步驟1，根據11 個省級行政區各指標數據的平均值，利用可變集相對隸屬度方法，結合PF 五級評分表，計算勾股模糊決策矩陣，見表3。

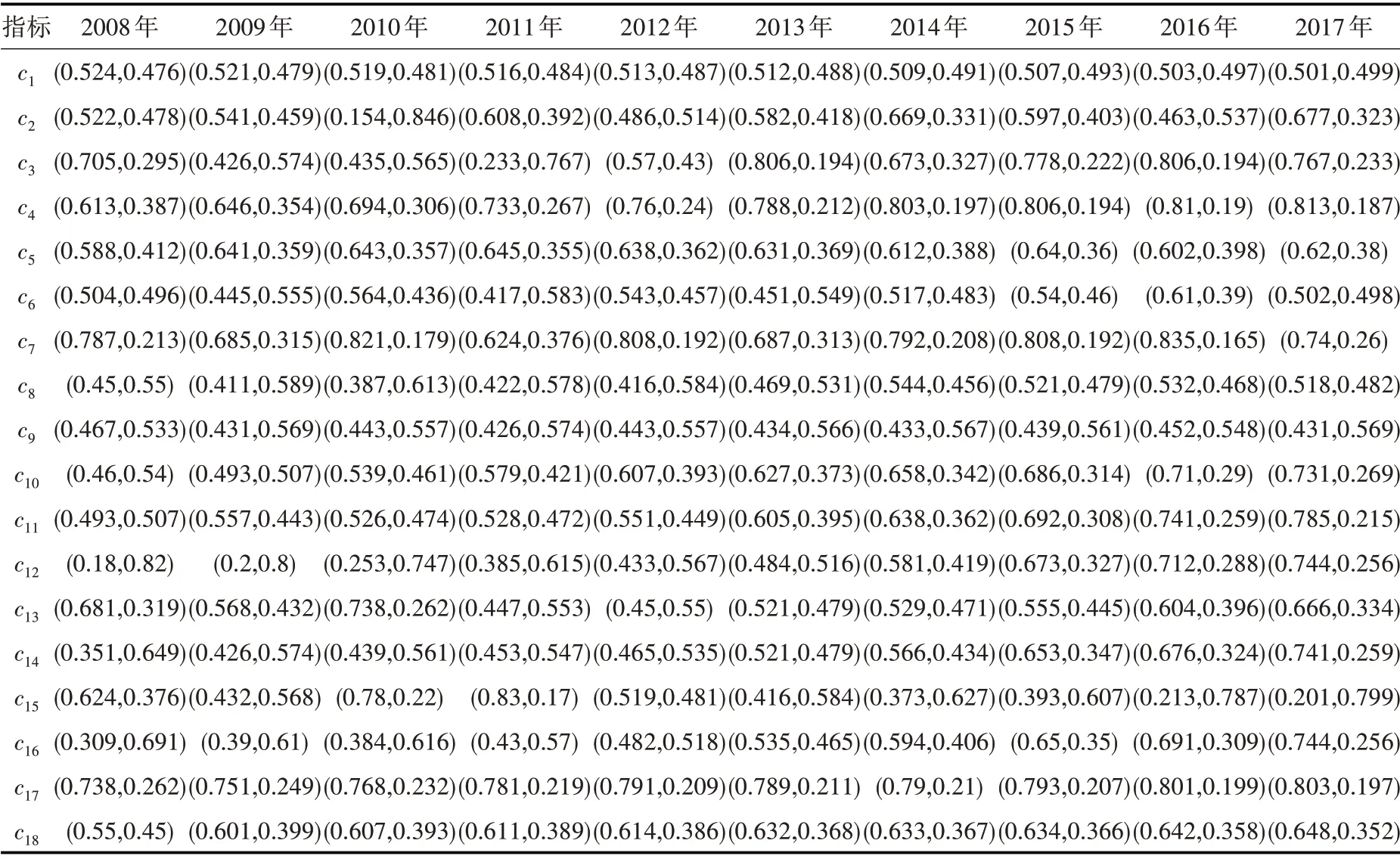
表3 長江經濟帶2008—2017年水資源韌性勾股模糊數

步驟2，基于11個省級行政區10年的總數據，利用式（12）計算各指標的權重，見表4。

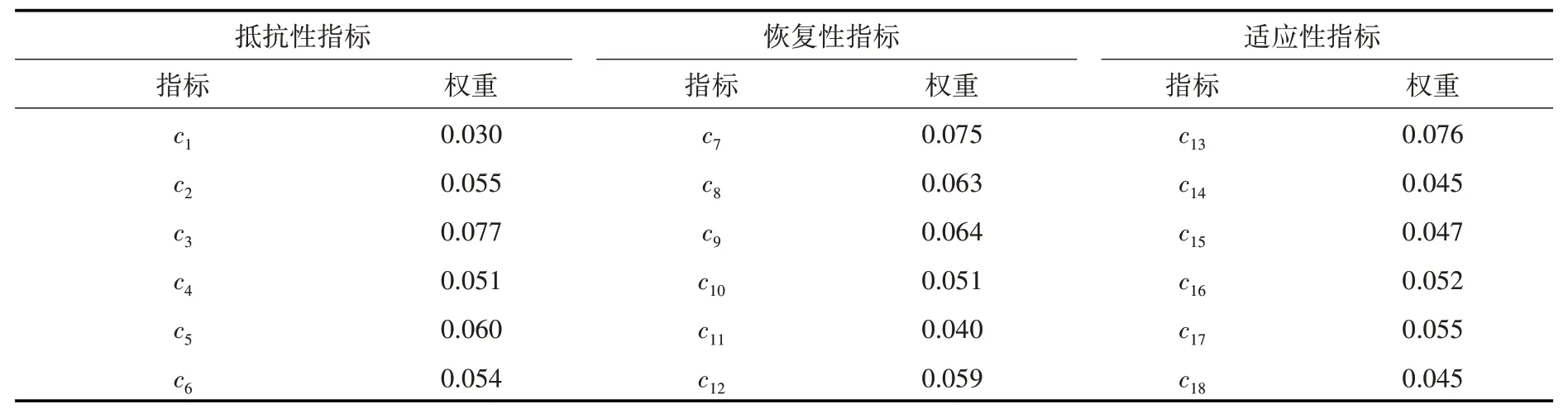
表4 長江經濟帶2008—2017水資源韌性指標權重

步驟3，計算各指標的正理想點和負理想點，見表5。

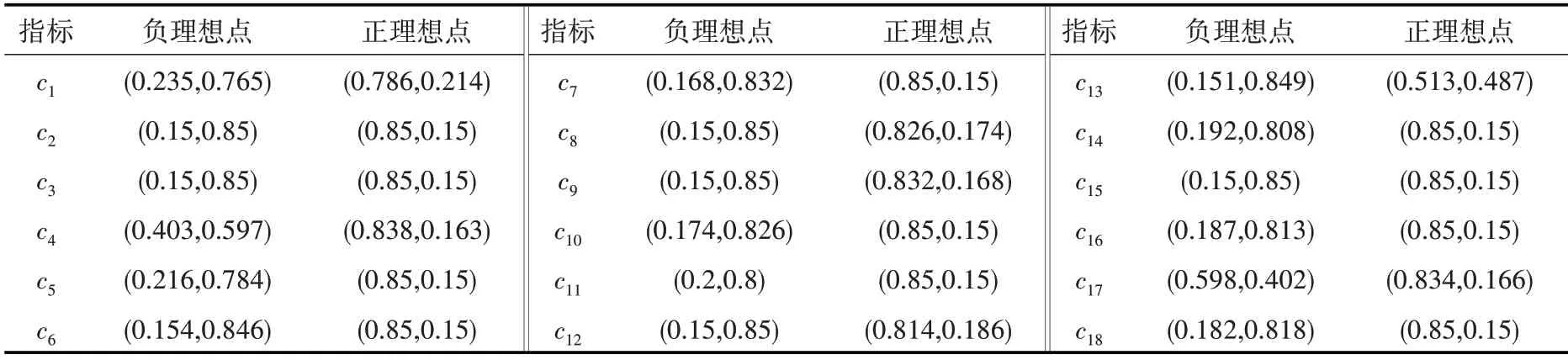
表5 長江經濟帶水資源韌性-各指標的正理想點和負理想點

步驟4，利用式（13）—（15）計算各年度的群體效益S、個體遺憾I和韌性排序值R。具體見表6。

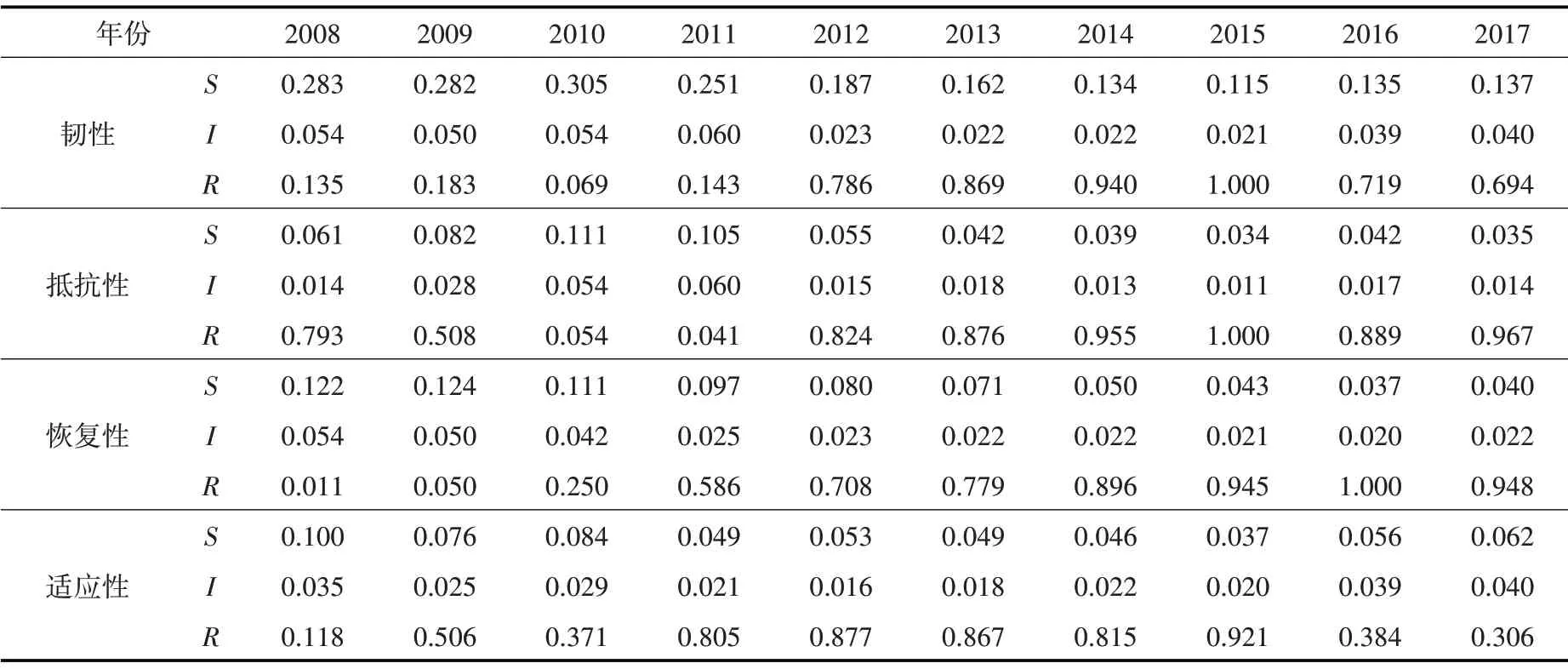
表6 長江經濟帶2008—2017年水資源韌性結果

步驟5，長江經濟帶各年度的韌性排序結果見圖2。各省區韌性及各方向的時空演化見圖3。

4.4 分析與討論由圖2可知：長江經濟帶2008—2017年水資源系統韌性總體上呈現逐年提升的態勢。2008—2011年，韌性值穩定于較低水平，2010年出現最低值；2011年之后，長江經濟帶水資源系統韌性得到了明顯的提升，在2015年出現峰值。隨后適應性水平的大幅下滑，韌性開始出現了一定程度的降低，其主要原因是財政收入增長率放緩，由2015年的12.56%下降至2016年的5.04%，同比下降60%；該指標水平大幅降低，其他的適應性指標水平仍呈現緩慢上升。因此，總體來看，適應性子系統的韌性排序值從0.921驟降至0.384，形勢嚴峻，是目前韌性的重點調控方向。

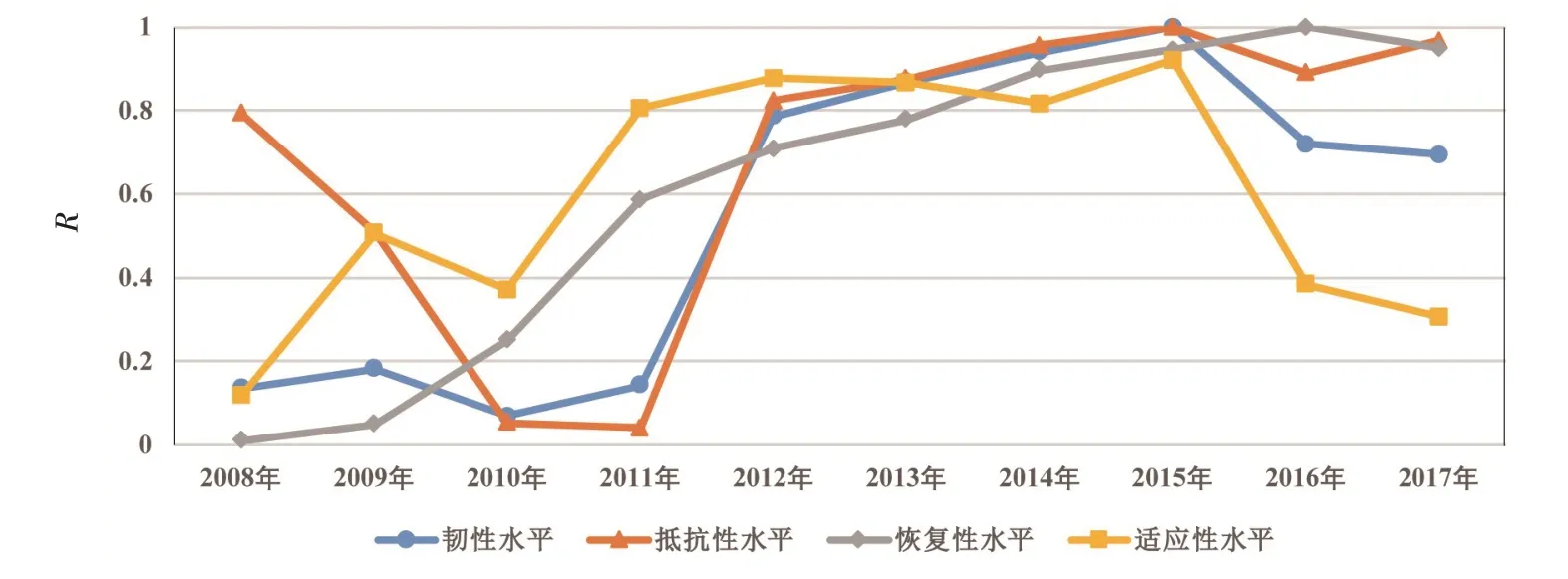
圖2 長江經濟帶2008—2017年水資源系統韌性趨勢

由圖3（a）可知，長江經濟帶11 省的水資源系統韌性均處于逐年上升的態勢，江蘇等部分省份在從2015年開始出現不同程度的下降；根據圖3（b），近年來，長江經濟帶水資源系統的抵抗性同樣呈現逐年提升的趨勢，但是上海、浙江和湖南等省區的抵抗性出現了嚴重的下降。其中上海市下滑最為嚴重，由于水資源稟賦較差，且人口密度持續增加，水資源系統抵抗性逐年下降。上海市人口的持續增長和工業化水平的日益提高，給水資源供需關系和水資源可持續利用等帶來了沖擊。圖3（c）展示了恢復性的穩定增長態勢，但江西等省區在2016—2017年出現了急劇下降，其中2017年人均水資源量同比下降了26%，但工業用水量卻增加了52%；根據圖3（d）可知，云南、貴州、安徽和湖南等省區的適應性水平得到了明顯的提升，而江蘇、上海和浙江等省區則處于較低水平。各省可根據自身實際情況，因地制宜，精準施策，制定相應的水資源系統韌性調控策略。

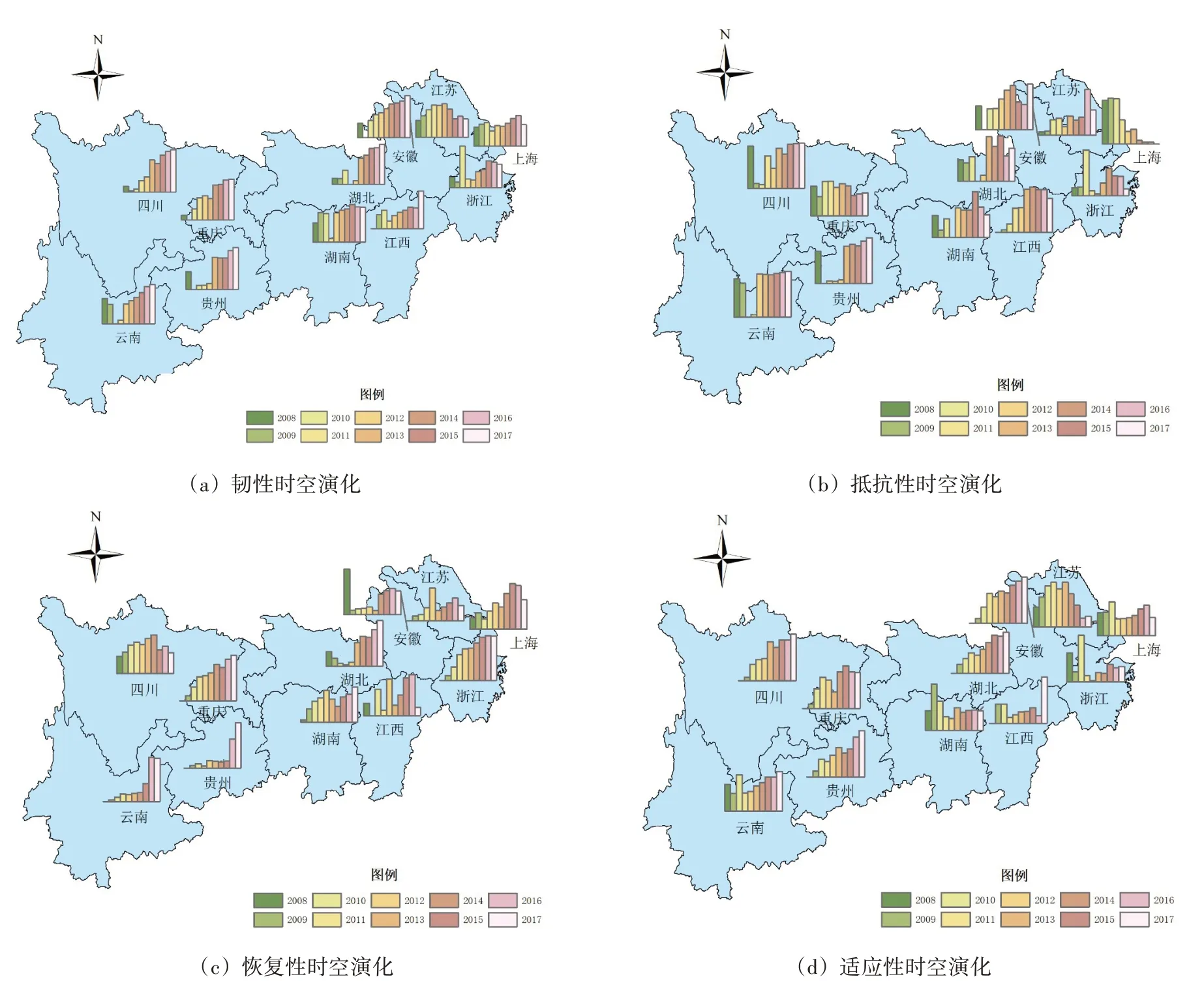
圖3 長江經濟帶2008—2017年11省級行政區水資源系統韌性的時空演化

將長江經濟帶劃分為東段（上海、江蘇、浙江）、中段（安徽、江西、湖北、湖南）和西段（重慶、四川、云南、貴州），并從水資源系統韌性及抵抗性、恢復性和適應性等四個方面進行區域之間的橫向對比，以期發現長江上中下游城市群的水資源韌性優勢與短板。具體見圖4。

根據圖4（a），長江經濟帶2008—2017年的水資源系統韌性呈上升趨勢；中西段韌性水平持續提升；東段相對穩定，無明顯改善，且2013年以來，自身優勢減弱，被中、西段超越。由圖4（b）（c）（d）可以發現，東段的抵抗性明顯弱于中、西兩段；東、中、西三段的恢復性均為逐年提升的態勢；適應性方面，東段區域近年來有一定程度的降低。

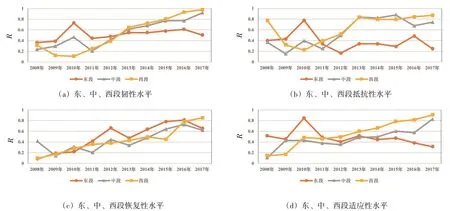
圖4 長江經濟帶2008—2017年東、中、西水資源系統韌性橫向比較

西段區域自然條件優越，水資源較為豐富，應進一步強化水源涵養、水土保持，合理開發利用水資源，促進水資源系統韌性；中段湖泊濕地眾多，肩負著重要的調水功能，應加強協調江湖關系，保護水生生態系統，進一步優化和規范沿江產業發展，確保長江中游水資源系統韌性的穩步提升。東段區域人口密集，經濟相對發達，工業化水平較高，產業同構化問題突出，水資源系統面臨著巨大的壓力，應進一步優化產業結構，提升用水效率，實現水資源的高效利用與可持續發展。

為精準挖掘韌性的重點調控指標，以2017年研究單元，對18項指標分別進行排序，進而對折衷韌性排序值進行異常檢測（設θ=0.5），挖掘主要調控指標。統計發現，在11 個省級行政區各指標的排序值中，“小于0.5”出現5 次以上的指標共有6 個，即工業用水、農業用水、生態環境用水量、環境治理投資、財政收入增率和科技研發投入。在這些指標上，長江經濟帶各省級行政區之間懸殊較大且低水平地區相對較多，因此這6項指標是總體韌性水平的主要擾動因子。具體見圖5。

由圖5可知，江蘇、江西、安徽等省份的工業用水量較大，同時江蘇、湖南和四川等省份的農業用水量較大，因此就產業結構而言，建議對江蘇、江西、安徽等工業用水量大地區的舊動能、落后產能進行產業升級，對等農業用水量大的地區發掘節水潛力；就環境治理以及水生態保護而言，安徽、浙江、四川、江西等地區的生態環境用水量較大，而貴州、江西及湖北地區治理水平相對較弱，需著力加強水源地、水功能區保護，抓好生態保護；在財政和科技投入方面，重慶和云南等地區相對較為滯后，建議當地相關部門深入研判當地水資源系統的韌性現狀，制定有效的調控方案，同時加大對科技研發的政策和資金支持，提升當地產能水平，促進水資源系統的韌性提升和可持續發展。此外，就防災減災水平而言，湖北、安徽、四川、云南、貴州受到干旱影響較大，江西、湖南、湖北等地受洪災影響較大，應采取相關措施對該區域的洪澇災害進行重點防治；各區域還需建立多層次數據共享平臺，為水資源系統韌性提升提供支撐保障。

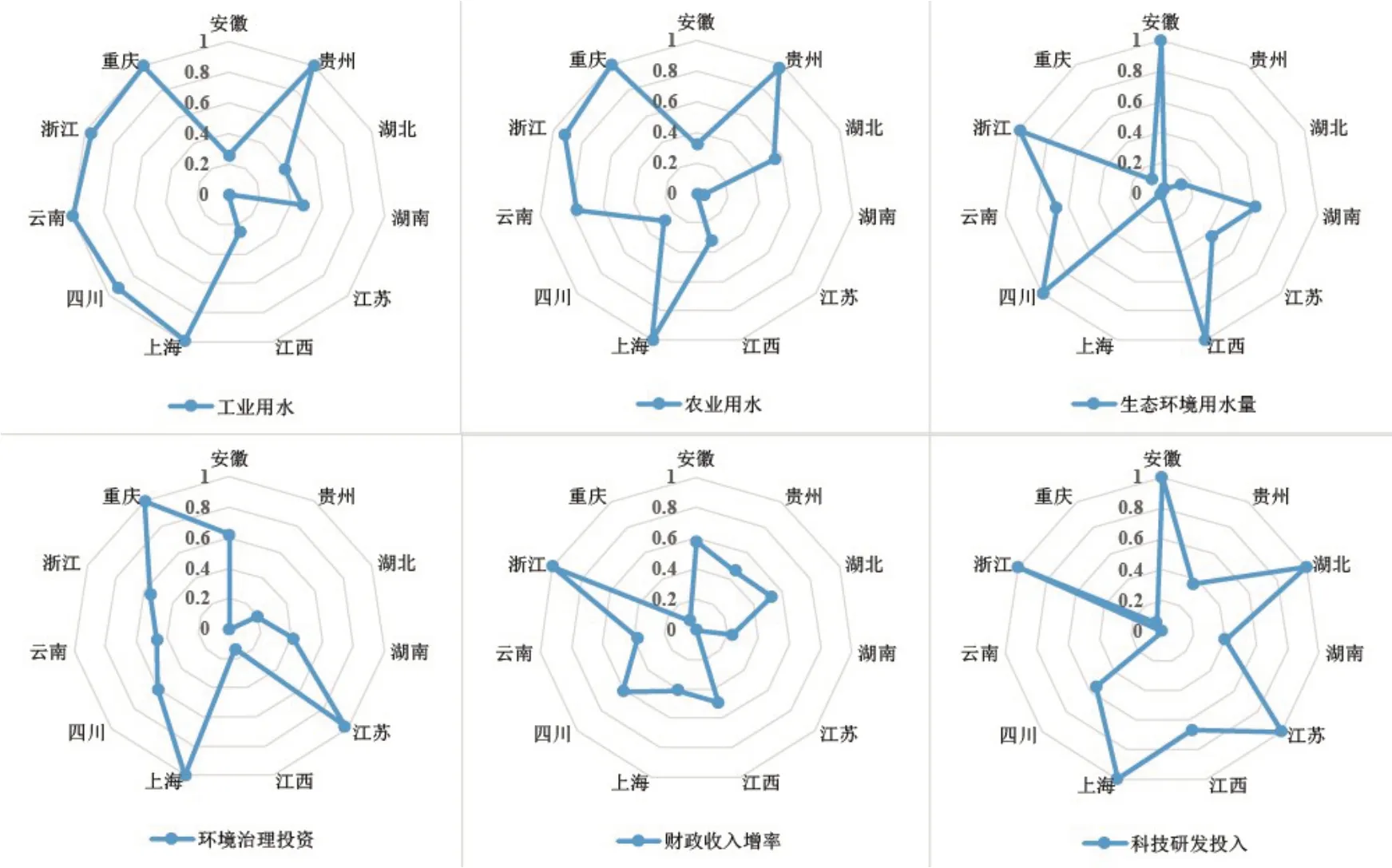
圖5 長江經濟帶2017年各省區6項重點韌性調控指標的等級排序分布

4.5 模型檢驗在本節中，通過調整決策系數τ()0 ≤τ≤1 值，檢驗韌性水平排序的改變情況，實現模型的靈敏性分析，結果見圖6。

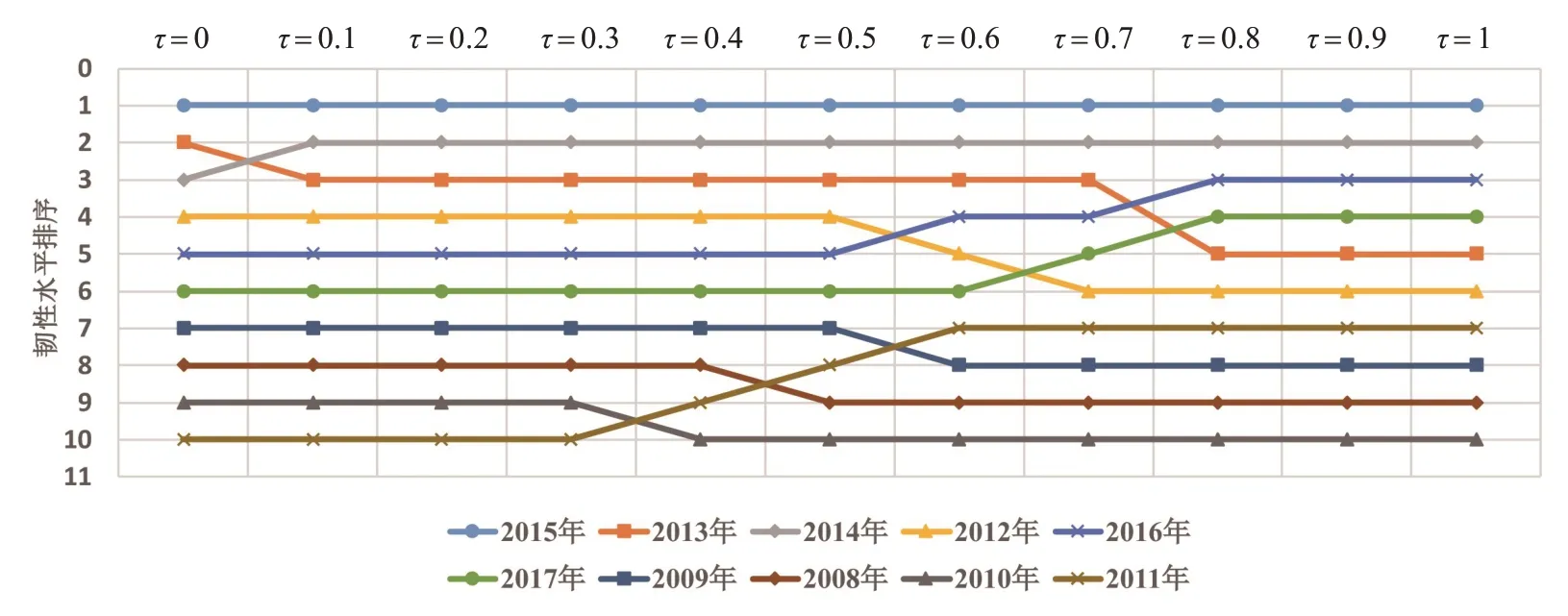
圖6 不同τ值情況下長江經濟帶2008—2017年水資源系統韌性排序

圖6表明，決策系數τ的不同取值對應不同的排序，從而對所評價結果產生影響，但韌性水平最高的年份沒有改變，始終是2015年。韌性水平最低的年份，在τ≤0.3時為2011年，在τ≥0.4時為2010年，這符合人們的決策偏好模式。事實上，決策系數τ反映了群體效用最大化和個體遺憾最少化之間的折衷。因此，τ的差異性取值顯示了決策者的主觀偏好在決策中的作用。

將本文的可變勾股模糊VIKOR 模型與傳統勾股模糊VIKOR 方法的進行比較，結果表明可變勾股模糊VIKOR方法的優勢體現在：（1）利用可變集相對隸屬度方法確定勾股模糊數，將決策矩陣中的勾股模糊數由原先的離散取值拓展至較為連續的模式，更好地刻畫了等級之間的模糊對立統一；（2）勾股模糊決策矩陣的確定不依賴于專家經驗，由客觀數據與等級標準之間的隸屬關系確定，一定程度上克服了現有勾股模糊VIKOR 方法的主觀性問題；（3）由圖7可知，本文提出的可變勾股模糊VIKOR 方法與現有勾股模糊VIKOR 方法的決策結果基本一致，但在各年度上均存在一定的正向或負向的差異，較好地彌補了由相鄰等級之間邊界過于絕對造成的某些指標的不可分辨問題。

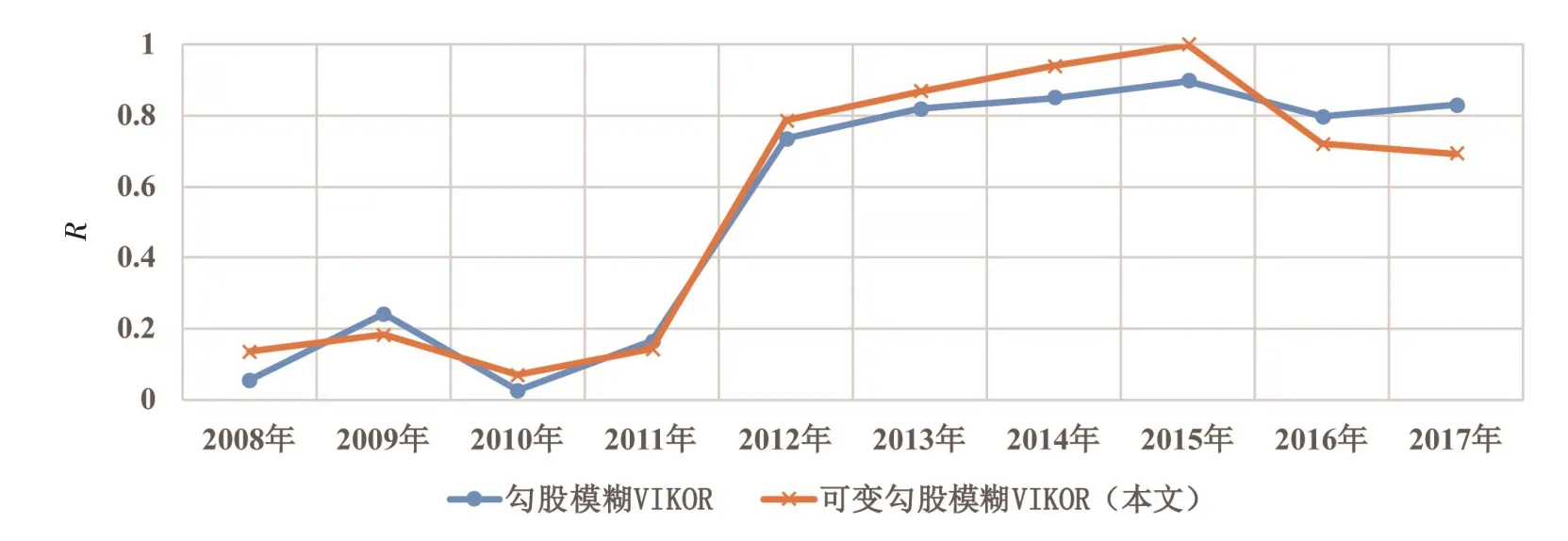
圖7 本文方法與已有方法結果比較

5 結論

本研究提出了一種基于可變集和勾股模糊集的VIKOR 多指標決策模型，以期對水資源系統的韌性進行評價與調控。在該模型中，決策者的偏好僅在對群體效益和個體遺憾的折衷上有所體現，在一定程度上提升了勾股模糊VIKOR 模型的客觀性。通過在長江經濟帶水資源韌性評價與調控中的應用，驗證了可變勾股模糊VIKOR方法的適用性和可行性，并通過靈敏性分析，說明了不同決策系數τ的影響。此外，與現有勾股模糊VIKOR方法相比，本文提出的方法具有客觀、連續等特點。

在水資源系統韌性的評價過程中，構建不同的指標體系可能會得到不同的評價結果，因此在評價結果的指示值上可能會存在一定的差異性，然而客觀的水資源系統韌性狀態及演化情況應基本趨于一致。本文依據科學性、合理性以及可獲得性原則，從抵抗性、恢復性和適應性三個方面探索水資源系統韌性評估策略，構建了共含18 項指標的多級評價指標體系，以期較為全面地反映水資源系統的風險應對能力。研究結果表明，長江經濟帶2008—2017年水資源系統韌性總體上呈現逐年提升的態勢。在2015年出現峰值，隨后開始出現了一定程度的降低，其主要擾動因子在于適應性子系統，因此應通過調控適應性子系統的各項指標，實現水資源系統韌性的穩定提升。此外，長江經濟帶11個省區的水資源系統韌性具有時空分異特征。中西段韌性水平持續提升；東段相對穩定，無明顯改善；東段的抵抗性明顯弱于中、西兩段；東段區域近年來適應性水平有一定程度的降低等。

由于水資源系統日益復雜，決策者很難將所有因素全部考慮，因此，采用可變勾股模糊VIKOR方法進行多指標決策，可以保證決策結果更加合理。勾股模糊集的其他重要研究途徑是與前景理論、層次分析法和理想點法TOPSIS的耦合研究，可使得勾股模糊集在諸多領域更加適用。