基于黃金分割法改進的GM(1,1)公路貨運量預測
雷永巍
(廣東省交通規劃設計研究院集團股份有限公司,廣東 廣州 510000)
1 概述
隨著產業結構、技術結構、產品結構和需求結構的不斷演變,交通運輸業占GDP 的比重穩步提升。與此同時,隨著運輸方式構成的持續調整,公路運輸在我國綜合運輸體系中發揮著更加關鍵的作用。據統計,2019 年我國公路完成貨物運輸量344億噸,比上年增長4.2%,在綜合運輸體系中所占比重分別達到73%。
公路運輸行業的快速發展,伴隨著現代電子商務的興起,物流產業迎來了高速發展期。公路貨運站和物流基地的合理布局成為公路和場站協調促進社會經濟發展的關鍵問題。貨運量作為客觀衡量區域運力與公路交通發展水平的重要量化指標,對其進行科學的預測將有助于政府把握區域公路運輸能力的發展趨勢,預估環境因素、政策及制度等變化對公路貨運量的影響,也能夠為今后制定物流產業政策及進行基礎設施投資決策的提供量化依據。
公路貨運量預測可分為定性預測法和定量預測法。定性預測是指研究人員根據自身經驗與理論知識對貨運量的發展趨勢做出判斷,其受主觀因素影響較大。為此本文在公路貨運量預測中重點進行了定量預測研究。目前,國內外學者對貨運量定量預測研究主要有兩類,一類為單一預測模型,包括回歸分析法、時間序列法、灰色預測法、BP 神經網絡模型、RBF 神經網絡模型等等,其中趙建有[1]等構建了基于模糊線性回歸模型的公路貨運量預測方法;崔乃丹[2]等利用小波降噪分析法,提高原始序列的光滑度,在此基礎上對新生成的序列應用灰色GM(1,1)模型進行貨運量預測;張麗莉[3]根據公路貨運量形成的復雜和非線性等特點,建立了BP 神經網絡預測模型;吳華穩[4]等提出了基于RBF 神經網絡的貨運量預測方法。另一類為組合預測模型,其中裴玉龍[5]等提出了灰色模型與馬爾可夫鏈組合的公路貨運量預測方法;印凡成[6]等引用最優加權組合建模理論,以預測誤差的平方和最小為目標函數來確定最優權重系數,建立了貨運量測模型;邵夢汝[7]等將灰色預測模型與BP 神經網絡模型組合,構建了灰色- 神經網絡的貨運量組合預測模型。
總的來看,目前針對貨運量預測的研究范圍廣泛,方法各有特點,本文應用實際貨運量統計數據為基礎,首次提出了用黃金分割法來改進傳統GM(1,1)模型,對比試驗表明,改進模型在精度和適用性上更好。
2 GM(1,1)公路貨運量預測模型
灰色預測模型(GM)是在少量信息的基礎上,實現對研究對象未來發展情況的預測。目前被廣泛應用于社會、經濟、人口、農業等研究領域。
在GM(1,1)模型中,第一個“1”表示一階方程,第二個“1”表示一個變量。GM(1,1)模型的具體建模步驟如下:
第一步,設公路貨運量時間序列X(0)有n 個觀測值,X(0)={x(0)(1),x(0)(2),…,x(0)(n)},其中應滿足X(0)(k)≥0,k=1,2,…,n。


其中,P 值越大,模型預測準確性越高,且通常δ(k)的值小于10%,則認為誤差水平是可接受的。
后驗差檢驗:
通過后驗差比C 和小誤差概率P 可對模型進行后驗差檢驗。記S1為原始時間序列x(0)的均方差:

若C 越小,表示模型預測效果越好,而小誤差概率正相反,P 值越大,表示模型預測效果越好。
灰色預測模型能適用于缺乏大量樣本的情況且運算簡便,但模型存在一定不足,如傳統的GM(1,1)預測模型中以固定的P 值生成背景值M(k)為基礎進行建模,忽略了其在建模中的作用。為此本文在前人的研究的基礎上,為克服傳統模型中背景值M(k)為相鄰兩個原始數值的平均值開始的弊端,通過黃金分割法來求解更優的背景值生成系數。
3 基于黃金分割法改進的GM(1,1)公路貨運量預測模型
黃金分割法又稱0.618 法,由美國的基弗(Kiefer)在1953年提出,后逐漸被廣泛應用。其主要思想為通過不斷縮小區間的長度來搜索目標函數的零點,且是按照可行域全長的0.618(及0.382)選取新點。
黃金分割法求g(x)零點近似值方法如下:
第一步,確定區間[a,b],精確度ξ,計算g(a)、g(b)的值,并驗證g(a)×g(b)<0 是否成立,若成立則進行第二步,否則結束計算;
第二步,求區間[a,b]黃金分割點c 值,c=a+0.618(b-a),并計算g(c);
第三步,比較,若g(c)=0,則c 就是函數g(x)的零點,結束計算;若g(a)×g(c)<0,則令b=c,此時零點在區間(a,c)內,進行第四步;若g(b)×g(c)<0,則令a=c,此時零點在區間(c,b)內,進行第四步。
第四步,計算新區間長度,若|a-b|<ξ,則得到零點近似值a(或者b),否則重復第二步至第四步。
采用金分割法改進的GM(1,1)公路貨運量預測模型確中值的步驟如下:

第二步,c=a+0.618(b-a),并計算g(a)、g(b)、g(c)。
第三步,進行判斷,若g(c)>g(b)>g(a)或者g(c)>g(a)>g(b),則停止計算,取p=a 或者p=b;若g(a)>g(b)>g(c)或者g(a)>g(c)>g(b),則令a=c,此時p∈[c,b],返回第二步;若g(b)>g(a)>g(c)或者g(b)>g(c)>g(a),則令b=c,此時p∈[a,c],返回第二步。
4 案例分析
將廣東省2000-2016 年共17 年間的公路貨運量數據作為原始數據輸入到預測模型中。得預測結果如表1 所示。

表1 GM(1,1)模型改進前后預測結果對比
4.1 改進前GM(1,1)模型預測結果檢驗:
殘差檢驗:


圖1 基于GM(1,1)的廣東省公路網貨運量預測結果
4.2 改進后GM(1,1)模型預測預結果檢驗


圖2 基于黃金分割法改進的GM(1,1)的廣東省公路網貨運量預測結果
4.3 預測效果對比
將模型改進前后預測值進行對比,結果如表2 所示。
從表2 可以得出改進后模型預測效果明顯優于改進前,平均相對誤差由改進前的13.12%降低為改進后的6.12%,同時在近兩年的預測中,改進后模型預測效果顯著,誤差小于4%。
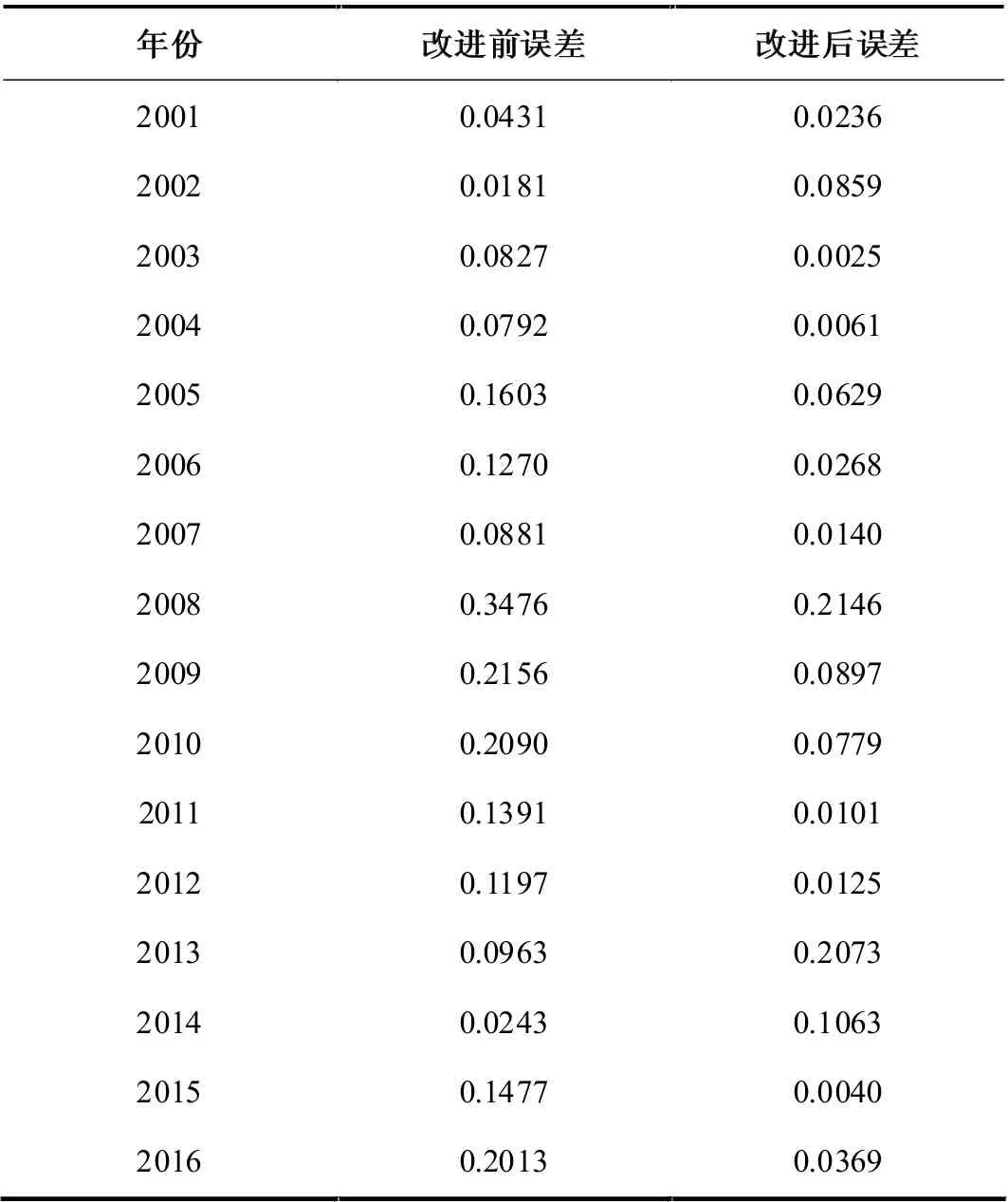
表2 GM(1,1)模型改進前后預測誤差對比
5 結論
本文將灰色預測方法運用于廣東省公路貨物運輸量預測,并針對灰色預測模型中固定背景值的局限,運用黃金分割法加以改進,構建了基于黃金分割法改進的GM(1,1)公路網貨運量預測模型,并與未改進的GM(1,1)預測模型進行預測效果比較。利用模型對廣東省公路貨運量進行預測,實驗結果表明基于黃金分割法改進的GM(1,1)公路網貨運量預測模型平均絕對百分比誤差為6.22%,均方百分比誤差為9.29%,具有較高的可靠性。
公路貨物運輸統計是反映交通運輸行業特別是公路運輸業發展狀況的晴雨表,隨著我國交通強國戰略目標的提出,公路貨物運輸的作用將會進一步加強,相關指標的統計與預測工作將更加重要。

