含多間隙彈性約束機械振動系統的動力學特性

尹鳳偉，馬 琳，馬娟娟

(蘭州交通大學 機電工程學院，蘭州 730070)

機械結構與系統的非線性振動是工程實際中的復雜問題.由于在幾何關系、約束條件、拓撲結構、激勵因素、耦合方式等方面存在非線性因素，因此深入研究非線性振動以便更精準地描述機械系統的動力學特征.掌握非線性振動的產生與傳播機理，對于設計制造安全和性能優良的機械系統至關重要.國內外學者通過定性分析、數值計算和實驗等方法研究了含間隙、約束振動系統的周期運動及分岔特征、擦碰奇異性和顫沖擊-粘滯振動系統.Nordmark[1]研究了帶有剛性限幅約束的單自由度周期受迫振子的運動特性.Luo等研究了帶有單側剛性約束[2]和對稱剛性約束副[3]的周期受迫振動系統的低頻振動特性，發現轉遷域結點為其中一個基本周期沖擊振動的二重Grazing余維二分岔.朱喜鋒[4]研究了含間隙機械振動系統的動力學特性與參數匹配規律.樂源[5]研究了一類三自由度碰撞振動系統的激變和陣發性，分析了擬周期-擬周期陣發性動力學現象.張惠和丁旺才等[6]針對一類單自由度含間隙和預緊彈簧的彈性碰撞振動系統的分岔控制問題，提出了一種基于Lyapunov指數及徑向基函數神經網絡的分岔預測及控制方法.葉建聰和石慧榮等[7]揭示了間隙和干摩擦對振動系統的周期運動和分岔特性的影響.李得洋和丁旺才等[8]采用線性反饋控制方法研究了一類兩自由度含彈性約束碰撞振動系統共存吸引子轉遷控制問題.Wagg[9-10]研究了一類帶有多剛性約束的兩自由度振動系統的低頻振動特性，分析了其低頻域內的顫碰-粘滯振動及Rising現象.頡成利和石慧榮等[11]計算了含預壓約束的兩自由度受迫振動系統的動力學特性，分析了預壓量與顫-沖擊振動的關系.Yin[12]針對含多間隙-非對稱剛性約束的兩自由度受迫振動系統，分析和計算了機械振動系統質塊沖擊剛性約束時引發完整顫-沖擊振動的判斷條件和動力學特性.呂小紅[13]研究了一類碰撞-漸進振動系統的粘滯振動及分岔特性.趙國慶[14]計算了兩級齒輪傳動系統的非線性動力學特征.覃澤鋒等[15]研究了考慮油膜力-碰摩故障的雙盤轉子系統非線性動力學行為.王紅兵和李國芳等[16]通過仿真計算，分析了高速車輛車輪踏面磨耗預測及系統參數影響.Liu和Pavlovskaia等[17]提出了由置于基架的彈性限幅板、線性DC伺服電動機和簡諧激勵的金屬棒構成的艙型振動沖擊模型；通過改變支承彈簧的剛度和激振頻率，對艙體的動力學進行了實驗研究.

本文在Wagg研究的基礎上，基于多參數耦合、多目標協同仿真分析，研究含多間隙-彈性約束兩自由度受迫振動系統的非線性動力學特性.而Wagg研究的帶有剛性約束的振動系統可視為帶有彈性約束振動系統的一種典型狀態.

1 系統的力學模型

圖1為一類兩自由度含多間隙彈性約束振動系統的力學模型.質塊M1與質塊M2通過剛度為K1的線性彈簧和阻尼系數為C1的線性阻尼器聯接，質塊M2經剛度為K2的線性彈簧和阻尼系數為C2的線性阻尼器連接于支承基礎.簡諧激勵力Pisin(ΩT+τ)作用于質塊Mi(i=1,2)，其中Pi、Ω和τ表示系統的簡諧力振幅、頻率和初相位.質塊M1右側和質塊M2左、右側均置有剛度系數K0的彈性約束，約束剛度取值范圍為K0∈(0,∞).當簡諧力較小時，系統呈現無沖擊受迫振動.隨簡諧力增大，當質塊M1的位移滿足X1=B1時，或質塊M2的位移滿足|X2|=B2時，質塊M1或質塊M2與其對應的彈性約束處發生軟沖擊[18].

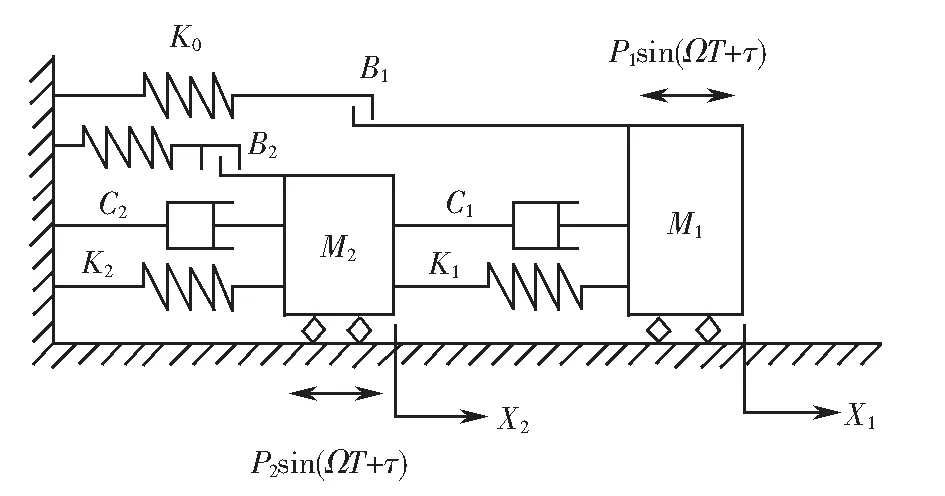
圖1 力學模型Fig.1 Mechanical model

引入無量綱量參數、變量和時間：

(1)

系統的無量綱運動微分方程：

(2)

其中，

(3)

(4)

根據無量綱化的系統參數(1)，可確定系統部分參數的取值范圍：μm∈(0,1)，μk∈(0,1)，μc∈(0,1)，μk0∈(0,1)，f∈[0,1].

2 系統的Poincaré映射

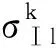
(5)

X(i+1)=f(X(i),ν),

(6)

(7)

(8)

上式(6),(7)和(8)中，X∈R4,ν是系統參數，ν∈R8.

3 數值分析

對圖1振動系統，在其參數定義域內取一組無量綱參數作為基準參數：μm=0.5,μk=0.5,μc=0.5,f=0.5,μk0=0.95.在同一范疇下，基于多參數耦合、多目標協同仿真分析，揭示了振動系統間隙閾值(δ)和激勵頻率(ω)等關鍵參數與系統周期振動的映射關系.數值計算結果(如圖2a)表明了系統在(ω,δ)-參數平面內的周期沖擊振動模式類型、分布規律和分岔特征.本文中(ω,δ)-參數平面圖中未標注的60%黑色區域表示未辨識的長周期振動或混沌.同時也未進一步對概周期振動和混沌進行辨識區分，本文暫均稱為混沌.數值計算結果表明當間隙閾值較大時(δ>1.5)，系統在高頻域內主要表現為0/1無沖擊自由振動；在低頻域內表現為0/1、1/1基本周期振動和少量的1/2、2/2周期沖擊振動.當間隙閾值較小時(δ≤1.5)，質塊M1在高頻域內表現為1/2、2/2、3/3、4/3、2/4、3/4、4/4等亞諧周期振動；在低頻域內，質塊M1主要表現為1/1、2/1、3/1、4/1、5/1…q/1(q≥6)等基本周期沖擊振動和少量的3/2、4/2…q/2(q≥6)等亞諧周期振動，如圖2(a)所示.

如圖2(b)所示，當間隙閾值較大時(δ>1.0)，質塊M2在高頻域內主要表現為1-0-0無沖擊受迫振動；在低頻域內表現為1-0-1、1-1-1、1-2-1、1-2-0、1-1-0等基本周期振動和少量的2-0-0、2-3-2等亞諧周期振動.當間隙閾值較小時(δ≤1.0)，質塊在高頻域內表現為4-2-0、2-1-0、2-1-1、2-2-1、2-2-2、4-4-4、4-4-3等亞諧周期振動；在低頻域內，質塊M2主要表現為1-3-0、1-3-1、1-3-2、1-4-0、1-4-1、1-4-2、1-5-0、1-5-1…1-p-q(p≥6或q≥6)等非對稱的各類基本周期沖擊振動和少量的2-3-2、2-5-2…2-p-q(p≥6或q≥6)等亞諧周期振動.

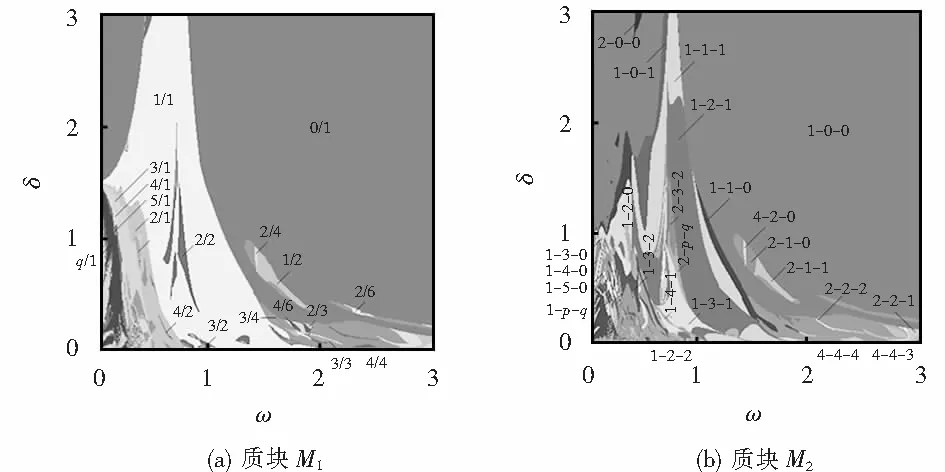
圖2 系統周期振動在(ω,δ)-參數平面上模式類型Fig.2 Mode types of periodic vibration of system on (ω,δ)-parameter plane

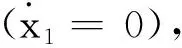
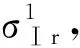
圖3 δ=0.43,系統分岔圖Fig.3 Bifurcation diagram of the system,δ=0.43

結合圖2(a)，圖3(a)和(b)，圖4代表性的揭示了質塊M1由5/1周期振動經Real-grazing分岔轉遷入穩定的6/1周期振動.圖4(a)取間隙閾值δ=0.43且激勵頻率ω=0.233 3時，質塊M1表現為5/1周期沖擊振動(圖4(b)是圖4(a)的局部描述)，隨ω減小到ω=0.233 22時發生5/1周期振動擦切接觸(圖4(d)是圖4(c)的局部描述)，當激勵頻率ω=0.233 20時質塊M1顯示為6/1周期振動(圖4(f)是圖4(e)的局部描述).在ω∈[0.332,0.333]區間內，隨激勵頻率ω的減小質塊M1經歷一次Real-grazing分岔轉遷；反之隨激勵頻率(ω)增大，質塊M1則由6/1周期振動經鞍結分岔轉遷為5/1周期振動.

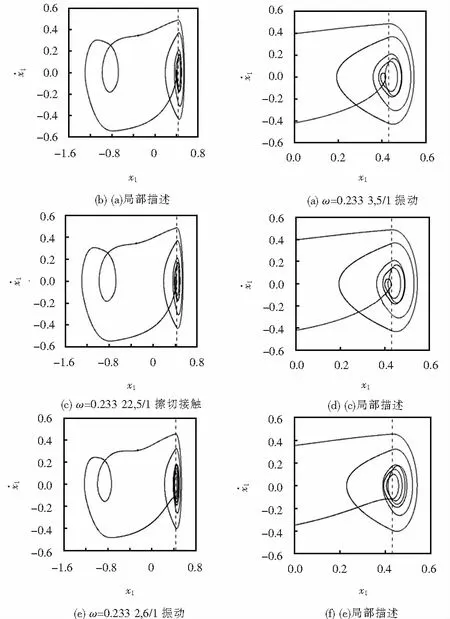
圖4 δ=0.43,質塊M1相圖 Fig.4 Phase diagram of mass M1,δ=0.43

同樣的Real-grazing分岔特性在質塊M2上也可觀察到.如圖5所示，取間隙閾值δ=0.43，當激勵頻率ω=0.413時，質塊M2顯示為1-2-2周期沖擊振動(圖5(b)是圖5(a)的局部描述)，隨ω減小到ω=0.411 2時發生1-2-2周期振動擦切接觸(圖5(d)是圖5(c)的局部描述).隨即當激勵頻率ω=0.410時，質塊M2表現為1-3-2周期振動(圖5(f)是圖5(e)的局部描述).在ω∈[0.410,0.413]區間內，隨激勵頻率(ω)的減小質塊M2經歷一次Real-grazing分岔轉遷；反之隨激勵頻率(ω)增大，質塊M2則由1-3-2周期振動經鞍結分岔轉遷為1-2-2周期振動.

圖5 質塊M2相圖，δ=0.43Fig.5 Phase diagram of mass M2,δ=0.43

圖6是對振動系統在基準參數下計算結果的進一步數值仿真計算，且取間隙閾值δ=0.1.在同一范疇下與圖3進行對比，計算結果顯示隨間隙閾值(δ)的減小，系統表現出更為復雜的動態特性.圖6(a)表明系統在低頻區主要表現為1周期振動，在高頻區表現為2周期振動，然而在1周期振動演化為2周期振動過程中，系統顯示出復雜的動力學特性，見圖6(b).取激勵頻率ω∈[1.7,2.95]區間時，隨ω增大，質塊M1的1/1周期振動嵌入混沌后退化為3/3亞諧周期振動和2/3亞諧周期振動.隨ω繼續增大，質塊M1表現為2/2、4/4、3/6等亞諧振動.隨后質塊M1由混沌經逆周期倍化分岔演化為1/2亞諧周期振動，見圖6(d).在相同的激勵頻率取值ω∈[1.7,2.95]區間內，隨ω遞減，質塊M2由2-2-1周期振動演化為1-1-0周期振動過程中，出現了2-2-2、4-4-4、4-4-3、8-8-7、6-6-4、2-2-1、3-4-1、3-3-2等亞諧周期振動，見圖6(f).

結合計算結果圖2、圖3和圖6，當間隙閾值(δ)取值越小，系統的非光滑特征越顯著，導致低頻域內基本周期沖擊振動群的量增大，即q/1(或1-p-q)周期振動顯著增多，且相鄰基本周期沖擊振動經Bare-grazing分岔轉遷過程中的亞諧周期振動模式類型表現出復雜性和多樣性特征.由于系統帶有多重間隙彈性約束，使系統M2在低頻域內出現了大量的非對稱基本周期沖擊振動群.隨激勵頻率ω進一步減小，當系統各質塊的沖擊次數(p或q)變得足夠大時，系統的基本周期沖擊振動表現為顫-沖擊振動特性.取間隙閾值δ=0.1，當激勵頻率ω=0.18時，系統質塊M1表現為10/1周期振動，質塊M2表現為1-9-2周期振動(見圖7).然而在相同參數條件下，當激勵頻率減小為ω=0.1時，系統質塊M1于其右側彈性約束處的沖擊次數q顯著增多，并表現為顫-沖擊振動特征；質塊M2則于其右側彈性約束處的沖擊次數明顯增大，也表現出顫沖擊振動特征(見圖8).

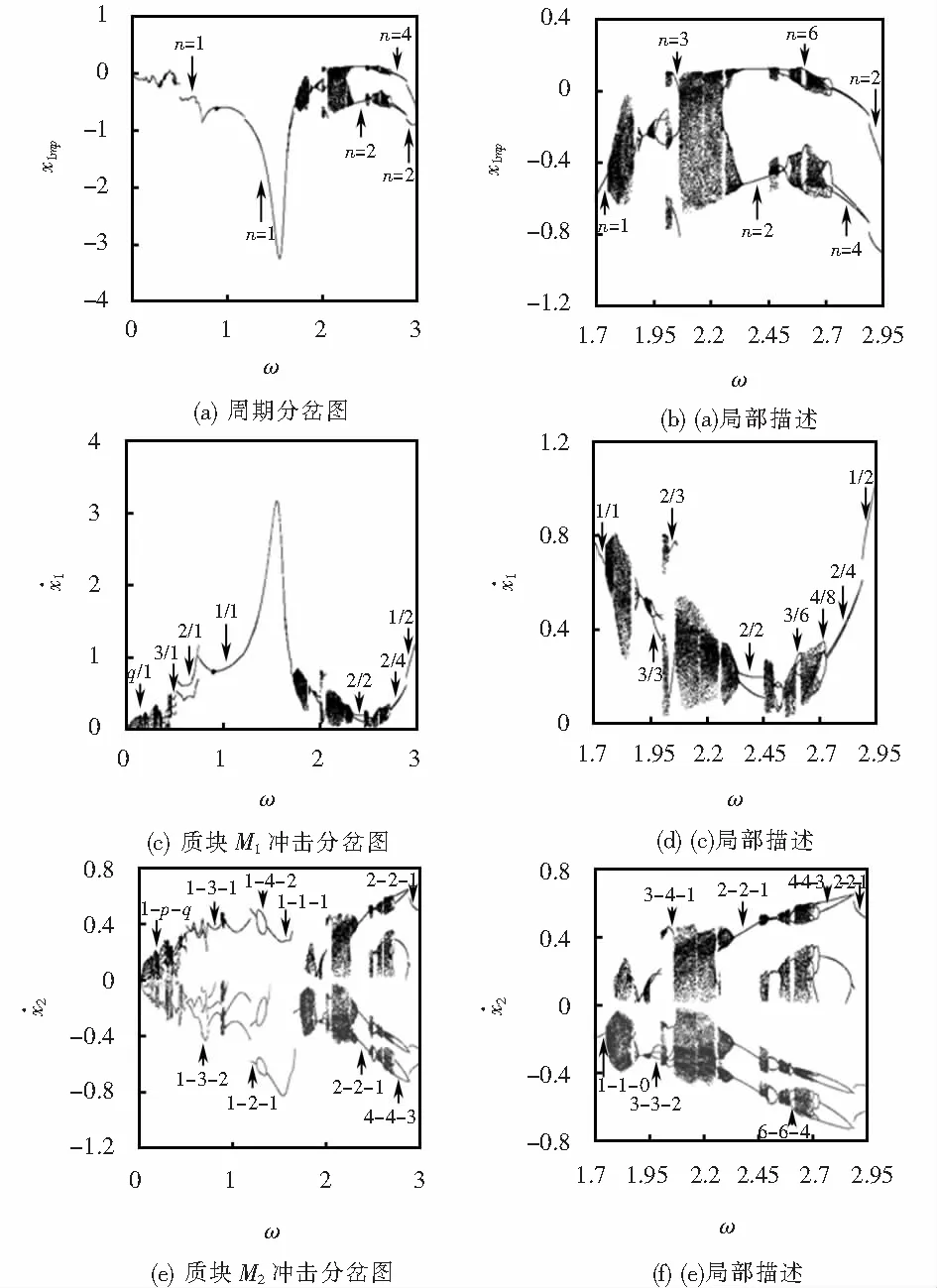
圖6 系統分岔圖,δ=0.10Fig.6 Bifurcation diagram of the system,δ=0.10

圖7 δ=0.1,ω=0.18,時間歷程圖Fig.7 Time response figure,δ=0.1,ω=0.18

圖8 δ=0.1,ω=0.1,時間歷程圖Fig.8 Time response figure,δ=0.1,ω=0.1

4 結論

本文針對含多間隙彈性約束機械振動系統的力學模型，研究了模型關鍵參數對系統動力學特性的影響.

1) 基于多參數耦合、多目標協同仿真分析，通過數值計算，揭示了系統在(ω,δ)-參數平面內的周期沖擊振動模式類型、分布規律和分岔特征.結果表明，間隙閾值取值越小，系統表現出越復雜的非線性動力學特性.由于振動系統幾何結構帶有多重非對稱彈性約束，導致系統表現出非對稱性的周期沖擊振動，系統周期沖擊振動的模式類型顯示出復雜性和多樣性特征.

2) 系統在小間隙且低頻域內，隨著激振頻率或間隙閾值的逐漸減小，系統的相鄰基本周期沖擊振動的q/1基本周期振動經Real-grazing分岔轉遷為穩定的(q+1)/1基本周期振動.或q/1基本周期振動經Bare-grazing分岔引發不穩定的(q+1)/1基本周期振動，并伴隨出現(nq+1)/n或2(nq+1)/2n亞諧周期振動等復雜的動力學特性.

3) 隨間隙閾值的遞減，系統在高頻區域出現亞諧周期振動和混沌；在低頻區域，系統各類周期沖擊振動模式類型和分布規律涌現出越發顯著的多樣性和競爭性.在低頻且小間隙域內，隨激勵頻率或間隙閾值減小，系統各質塊的沖擊次數(p或q)逐漸增多.當系統沖擊次數足夠大，系統表現出顫-沖擊振動特性.

4) 計算結果揭示了含多間隙彈性約束機械振動系統在基準參數取值下的非線性動力學特性.針對不同功能的機械系統能夠確定激勵頻率和間隙閾值等關鍵參數的科學匹配范圍，實現系統動態特性與功能目標的協同優化.