考慮基地住宿問題的高鐵列車乘務排班計劃編制

李 雯，代存杰，巨玉祥，成 洋，張芳英

(1. 蘭州交通大學 交通運輸學院，蘭州 730070；2. 中國鐵路蘭州局集團有限公司 蘭州車站，蘭州 730000；3. 中國鐵路蘭州局集團有限公司 蘭州客運段，蘭州 730000)

列車乘務排班計劃，是指對列車乘務班組的休息、值乘，乘務車間做出的具體規劃安排，主要在列車乘務計劃編制的第二個階段完成.完善的乘務排班計劃，能夠減少運營成本，并對乘務員的休息、工作時間進行科學有效地安排，提升乘務員對工作的滿意度，具有關鍵的實踐價值與作用.因乘務員的組織模式、乘務車間管轄的值乘區段存在差別，所以乘務排班計劃的編制同樣也呈現出不一樣的模式.既有研究表明，乘務排班通常選取兩類方式，即固定周期和單循環兩種.目前相關的研究成果有：

文獻[1]研究上海市軌道交通乘務排班優化問題，將乘務工作分為日班和夜班兩部分并歸結為一個二分雙向匹配問題，采用匈牙利算法進行求解.文獻[2]應用蟻群算法，針對高速鐵路單循環模式乘務排班計劃編制問題，以乘務交路接續時間最短和冗余時間分布最均衡為目標進行問題求解.文獻[3]將動車組交路計劃的編制問題轉化為多旅行商問題，采用信息素增強的蟻群算法求解，并通過現場采集的數據驗證算法的有效性.文獻[4]構建了乘務人員數量最少與工作時間適應的雙目標模型，基于南京—常州區間的列車運行數據，使用改進的蟻群算法進行實例驗證.文獻[5]通過分析車次、交路及乘務員之間的關系，以乘務班組費用最小化為目標，以交路和乘務工時為約束建立優化模型，設計遺傳算法進行求解.文獻[6]同樣將鐵路乘務排班問題抽象為多旅行商問題，以排班周期最短、乘務交路間冗余接續時間分布最均衡為優化目標，構建數學優化模型，使用一種啟發式修正蟻群算法進行模型求解，并以廣深城際鐵路為案例驗證算法的有效性.文獻[7]設計了引入文化基因算法的非支配遺傳算法(non dominated sorting genetic algorithm-II，NSGA-II)來解決多目標作業車間調度問題，該算法增加了基于模擬退火算法的局部搜索程序.文獻[8]基于時空網絡模型，對于在某個責任范圍內，針對使用乘務班組人數的下限展開求解.文獻[9]設計自適應遺傳算法，初始值為難以獲取的乘務組數的最小值，所借助的遺傳算法當中的染色體長度，能夠在迭代中進行自適應改變.文獻[10]設計的遺傳算法，含有嵌入式模糊邏輯處理器，用以促使算法交叉、變異機率的增加.文獻[11-12]分別研究手術調度和項目調度的相關問題，優化與完善NSGA-II算法，同時借助運算數據，由分布性以及收斂性，驗證優化方式的效果.文獻[13]建立了帶時間窗的多車場公交乘務排班優化模型，并使用禁忌搜索算法對該問題進行求解，結果表明該方法在處理帶有時間窗的多車場公交乘務組跨線排班問題時具有良好的應用效果.文獻[14]研究等待折返的動車乘務交路改進及優化的問題，基于集合分解問題擴展問題模型，同時運用遺傳—蟻群混合算法展開求解.文獻[15]針對公交線路多目標優化模型，采用改進的NSGA-II算法，以自然數進行編碼，采取錦標賽選擇策略進行選擇操作，并采用均勻變異的方式，得到了較好的求解結果.

在已有文獻中，通常將最小化班組數量，勞動均衡性做為求解目標，卻沒有對乘務班組因值乘不同出發時刻、到達時刻交路而產生的住宿問題進行優化.本文針對乘務基地住宿問題進行了討論，并設計了相應的優化求解方法，在客運段車隊(間)實際工作中，有較強現實意義.

1 乘務排班計劃多目標數學模型

1.1 問題描述

本文討論的列車乘務排班計劃是指，在指定周期排班模式[2]下，對周期內乘務班組與值乘交路的匹配關系做出具體的安排.客運段通常以運營成本最小作為乘務計劃編制的總體目標，其中人員成本和住宿成本在運營成本中占比最高.考慮到工作實際中，因值乘早發交路、晚至交路在乘務基地的住宿成本取決于在基地住宿的乘務班組數量，因此將班組數量和基地住宿班組數目作為乘務排班計劃數學模型中的優化目標.又因各班組完成的任務量應當是均衡的，勞動均衡性也作為求解的目標之一.

基于以上分析，在模型構建過程中，在將最小化乘務班組數量、勞動均衡性作為目標的基礎上，首次將最小化基地住宿乘務組數目作為求解目標，在已有研究基礎上，將乘務交路與乘務班組的指派關系和周期內的勞動時長限制作為模型約束，對該問題進行優化.

1.2 指定周期乘務排班計劃指派模型

綜上分析，在原有研究[5]的基礎上將乘務排班計劃編制問題看作經典的指派問題，在此基礎上建立多目標優化模型.模型中的符號定義如表1所列.

表1 模型符號定義Tab.1 Definition of model symbols

具體數學模型如下:

(1)

minZ2=

(2)

目標函數(1)為乘務班組數量的最小值.目標函數(2)為各乘務班組勞動時長差值最小.

(3)

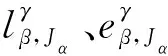
(4)

(5)

式(4)和式(5)為實際工作中乘務交路和乘務班組的一一對應要求，即每天乘務班組只能值乘一個乘務交路，且一個乘務交路只能由一個乘務班組值乘.

(6)

式(6)為給定乘務排班周期范圍內的工作時長約束，月度工時限制為166.6 h.

2 改進的NSGA-II算法求解列車乘務排班計劃

乘務排班計劃編制問題數學模型為多目標優化模型，該類問題中的每個子目標間一般是相互矛盾的，求得的解被稱之為非支配解或Pareto最優解，主要特征為優化任一目標函數的同時，并不影響至少一個其他目標函數.

結合該問題特點，設計基于實數編碼的NSGA-II算法對模型進行求解，并對算法進行改進，使用基于禁忌思想的變異方式，盡可能的減少非可行解的產生.針對求解時容易出現的收斂速度慢、易陷入局部最優的問題，引入基于小生境的精英保留策略及自適應交叉變異算子的改進方式.此種改進方式符合問題的特點，可以提高算法的收斂速度，同時提高解的分布.

2.1 算法設計及改進

2.2.1 算法設計

1) 初始種群的產生

采用實數三層編碼模式，第一層設指定周期內的排班計劃為染色體，第二層設排班計劃內每天的值乘計劃為基因，第三層為某天值乘計劃中乘務班組的排列次序.指定排班周期與乘務交路個數之積T×m作為初始種群中個體的乘務班組數，以實數代表一個班組出乘，其排列位置代表乘務班組值乘的交路和日期.

2) 適應度計算

適應度為遺傳算法中決定個體優劣的指標，本例中，直接利用目標函數Z1、Z2、Z3數值作為個體的適應度.

3) 非支配排序

非支配排序是本算法篩選后代個體的排序方式，根據適應度函數對個體進行非劣分層，比較個體函數值的大小，將當前種群中所有非劣解劃分為同一等級，令其為1；在剩余個體中找出新的非劣解，令其等級為2；重復以上過程，直至種群中所有個體都被設定相應的等級.

4) 錦標賽選擇

隨機選擇兩個個體，首先比較非劣等級，如果非劣等級不同，則取非劣等級較小的個體，若非劣等級相同，則以擁擠度CDl為標準，取擁擠度大的個體，形成新種群.

5) 交叉運算

針對問題編碼特點，采用單點交叉的方法，對排班計劃中某一天的值乘計劃進行交叉，在具體操作中，先對染色體進行隨機配對；其次隨機設置交叉點位置；最后再相互交換配對排班計劃的某一天的值乘計劃.算法中的交叉運算如圖1所示.

6) 變異運算

針對每天值乘計劃中的值乘班組進行變異，在變異操作中引入禁忌思想，設置兩種變異方式.首先隨機選擇某天乘務計劃中乘務交路的基因變異位置，然后針對每天的值乘交路設置禁忌表，將當天出乘班組編號放入禁忌表中，變異選擇為在當天不出乘的乘務班組.其次對值乘早晚交路做標記，值乘晚至交路的班組，判斷是否在次日的禁忌表中，若不在禁忌表中，則在值乘早發交路變異為相同班組.

2.2.2 算法改進

根據已有研究[11]，計算染色體的海明距離即小生境尺寸CDl來實現擁擠密度的排序并減輕計算量，同時改善解的分布多樣性.按海明距離由疏到密的標準，將個體復制到下一代，直到下一代群體規模達到進化群體規模終止復制.某非支配染色體集上第l個染色體的擁擠度CDl按下式計算:

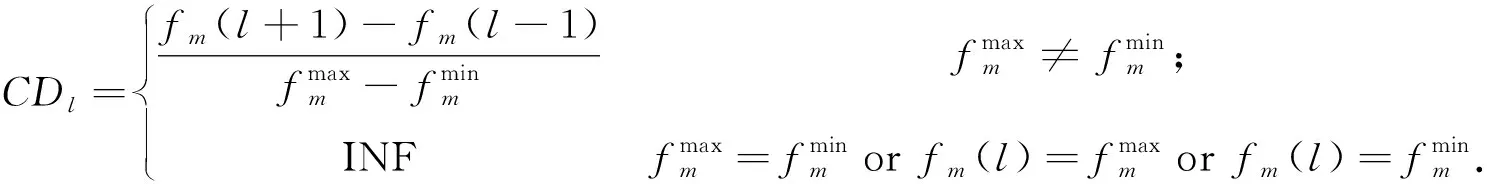
(7)

為避免NSGA-II算法因選定交叉和變異概率帶來的弊端，引入概率自適應策略，動態控制遺傳操作的頻率.使用自適應交叉算子克服不成熟的收斂，使用自適應變異算子保持種群內個體的多樣化，降低陷入局部解的可能，其中自適應交叉算子和變異算子分別為

宋榕華....................................................................................................................................................................科萊恩大中華區可持續發展及管理事務總監

(8)

(9)

算法經過多次迭代后，乘務班組數值不再有變化，并達到迭代次數時終止.

2.3 算法具體流程

步驟1設置進化代數計數器t=1,隨機產生滿足不超過周期內最大工作時長初始種群P(t)，設置種群中班組數量為T×m；

步驟2計算每個個體相應的目標函數值fm；

步驟3快速非支配排序.對種群P進行非劣分層，直至種群中所有個體被設定相應等級；

步驟4錦標賽選擇.隨機選擇兩個個體，若非劣等級不同，首先比較非劣等級，取級數較小的個體；若個體在同等級中，以擁擠度做進一步比較，取較優個體，形成種群P1(t)；

步驟5個體中的某一天的交路進行交叉操作，縮減乘務班組數目，并使用禁忌思想對某天內交路值乘安排進行變異操作，得到種群Q；

步驟7選擇前N個個體產生新一代種群NPt；

步驟8判斷產生更小乘務班組數目則轉到步驟2.當算法進入停滯狀態，乘務班組數目不再變動時，算法終止.

3 實例驗證及分析

采用北京南站至天津站間的列車運營數據對本文設計的模型算法進行驗算，利用經典的NSGA-II算法和改進的NSGA-II算法分別對該問題進行計算.并規定早于Ts=8:00發車的乘務交路為早發交路，晚于Te=20:30到達的乘務交路為晚至交路.列車乘務交路數據如表2所列.

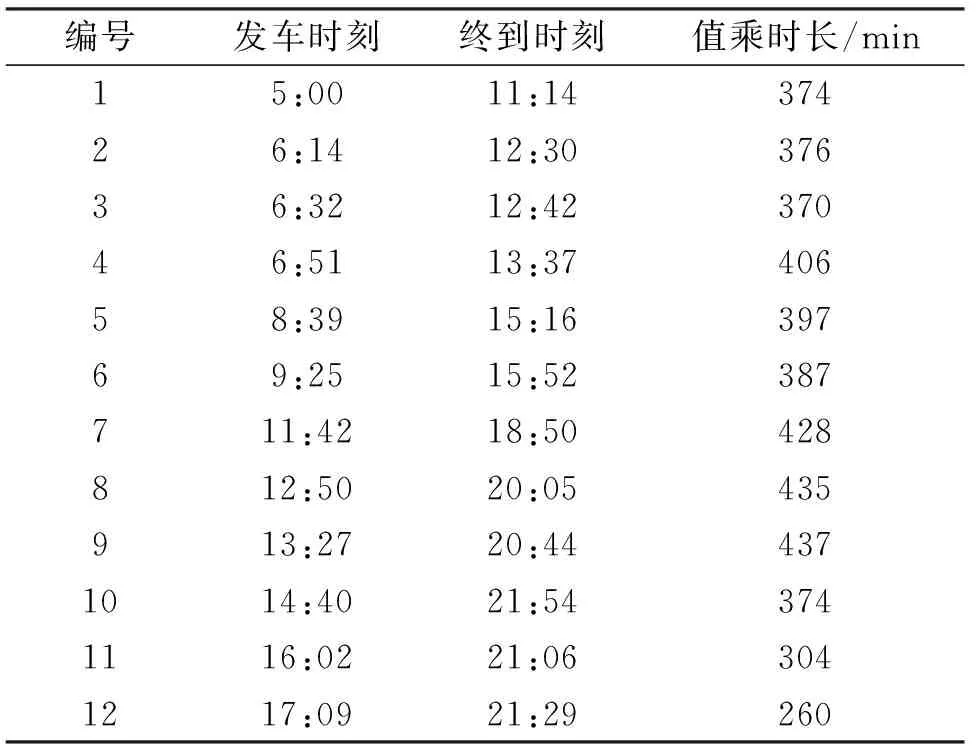
表2 列車乘務交路數據Tab.2 Crew scheduling data

對NSGA-II算法參數進行設置：T=10 080 min；Maxgen=500次；Popsize=130個；自適應概率及變異概率為PC1=0.9；PC2=0.6；PM1=0.1；PM2=0.001.

將經典NSGA-II算法和改進后的NSGA-II算法求解速度和求解結果進行比較，來驗證算法及算法改進的有效性.

算法改進前后的收斂速度如圖2所示.

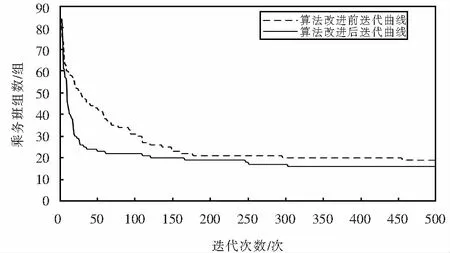
圖2 算法改進前后收斂曲線對比圖Fig.2 Convergence curve comparison chart before and after the algorithm improvement

通過對比算法改進前后的收斂曲線可得，經典的NSGA-II算法在迭代次數450代附近逐漸呈現出較好的收斂趨勢，而改進后的NSGA-II算法在300代附近收斂穩定；改進后的NSGA-II算法收斂效率高、速度快，表現出更好的收斂性能，且求得的目標函數值更優.因此針對該問題的算法改進是有效的.

對改進前后所得最后一代Pareto解集的平均值進行對比，并將算法執行時間進行對比可知，算法改進后收斂速度提升14%，所得Pareto解集各目標函數的平均值均優于經典NSGA-II算法.算法改進前后求得的解的平均值如表3所列.

表3 算法改進前后結果對比Tab.3 Comparison of results before and after the algorithm improvement

最終求解所得的pareto解如表4所列.

表4 乘務排班問題非支配解Tab.4 Pareto solution of crew scheduling problem

解碼后得出對應乘務排班計劃表，其中基地住宿班組數最多和最少所對應的乘務排班計劃表如表5～6所列.

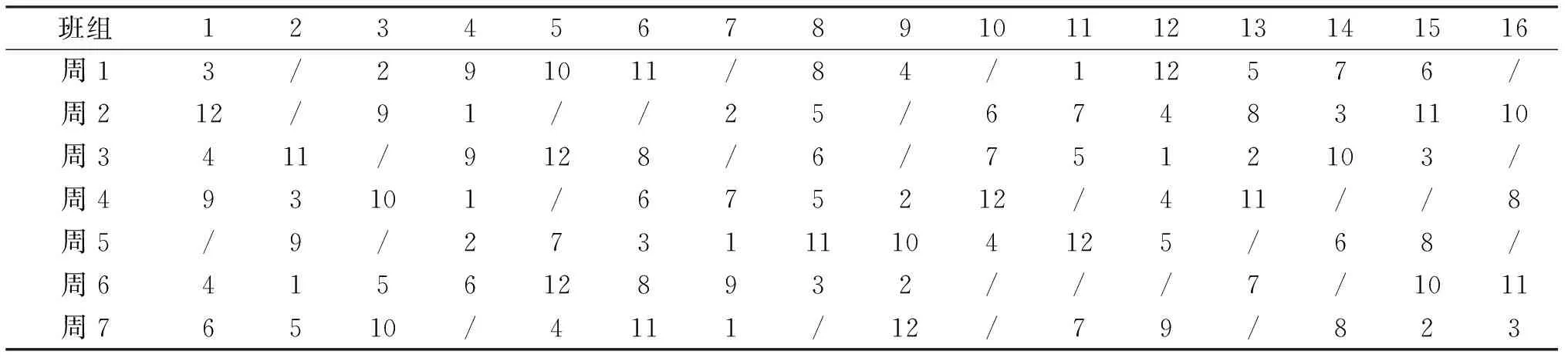
表5 當Z1=16，Z2=43 080 408，Z3=42時的乘務排班計劃表Tab.5 Crew scheduling plan when Z1=16，Z2=43 080 408，Z3=42

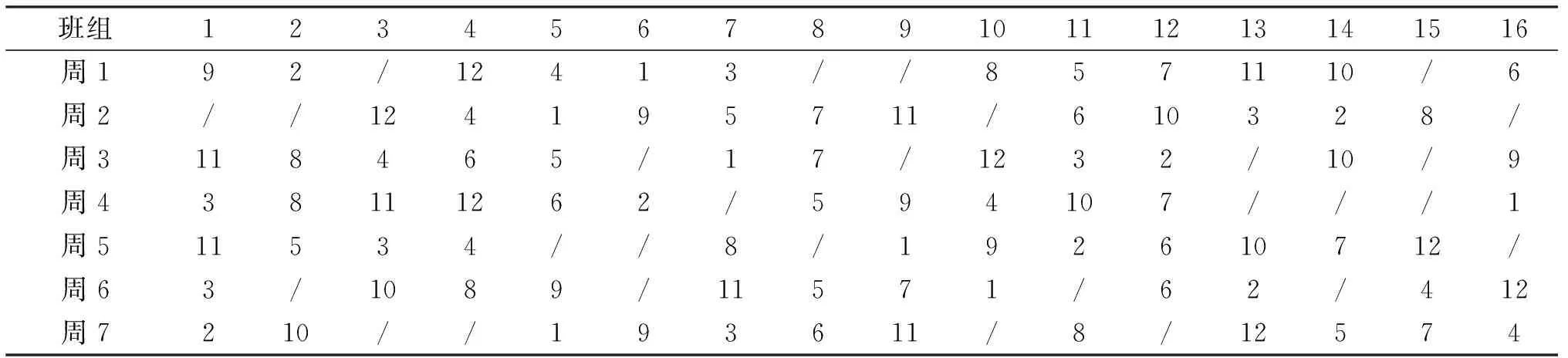
表6 當Z1=16，Z2=46 159 475，Z3=33時的乘務排班計劃表Tab.6 Crew scheduling plan when Z1=16，Z2=46 159 475，Z3=33

4 結論

考慮到乘務工作中因交路出發時刻、到達時刻不同而產生的基地住宿實際，討論因該問題產生的乘務基地住宿班組數量的優化問題，并基于指派模型，建立解決該問題的多目標優化模型.針對該模型，設計NSGA-II算法進行求解，并對算法進行了改進.最后以北京南站至天津站間的列車運行基礎數據為算例，對設計的模型、算法進行驗證，通過求解結果和算法改進前后計算結果的對比可得，算法改進后目標函數的求解結果及收斂速度均有了提高，從而證明了模型的正確性及算法的有效性.

乘務班組住宿優化問題，在客運段車隊(間)實際工作中，有較強現實應用意義.本文未考慮在給定乘務基地住宿能力情況下列車乘務排班計劃的編制，對這一問題的研究將是以后研究的重點.