基于現場直剪試驗和強度軟化的圍巖壓力解析

盧永飛，余云燕，陳志敏

(1. 蘭州交通大學 土木工程學院，蘭州 730070；2. 蘭州交通大學 甘肅省道路橋梁與地下工程重點實驗室，蘭州 730070；3. 西北民族大學 土木工程學院，蘭州 730030)

隧道開挖引起應力重分布，洞周附近出現應力集中，離開挖洞室較遠處應力基本保持不變.高磊[1]將開挖前后應力變化大于5%的區域稱為擾動區，變化小于5%的區域認為沒有受到開挖影響，稱為原巖.隧道擾動區的范圍及其應力大小對隧道穩定性評估和支護方案設計有很重要的作用；李鈾等[2]在應力場計算中采用了塑性力學折線理論，研究了圓形隧道擾動區和圍巖的臨界破壞深度，得出擾動區范圍與外荷載的大小與作用形式、泊松比和埋深有關，有時會超過通常所認為的擾動區的大小是井巷尺寸的3～5倍這個論斷；王鳳云等[3]通過引入應變軟化度對深埋圓形隧道圍巖彈塑性進行了分析，得出彈塑性分界面處的圍巖壓力與軟化度和支護力均無關，塑性區的半徑與支護力關系密切，軟化區與殘余區的大小受軟化度影響，軟化度增大，軟化區范圍變大，相應的殘余區范圍變小；Alonso等[4]運用自相似解將應變軟化圍巖的特征曲線的偏微分方程轉化成微分方程，但因其過程復雜沒有得到普遍的推廣；Lee等[5]就深埋軟巖圓形隧道用一種有限差分法將洞周發生塑性變形的巖體按照徑向應力增量相等劃分為多個同心圓，再通過迭代求解；陳志敏[6]針對高地應力軟巖現有本構關系不具有廣泛代表性和卡斯特耐爾公式的不足問題，以原巖應力和隧道容許位移為出發點，推導了隧道形變壓力改進計算公式；何滿潮等[7]針對軟巖巷道在靜壓條件和動壓條件以及巷道底板穩定和不穩定的不同情況，分別討論了軟巖巷道支護荷載的確定方法.文獻[8-13]基于Hoek-Brown，Mohr-Coulomb，Drucker-Prager等不同屈服和強度準則，研究了應變軟化、支護壓力、黏聚力、內摩擦角等參數對圍巖塑性區的影響，建立了圓形巷道圍巖的彈塑性分界線方程，得出了不同強度理論塑性區范圍和形狀及巷道塑性區的形態變化規律.文獻[14]更全面地考慮多種因素，對深埋圓形巷道圍巖力學和變形特性進行假定，進而建立圍巖塑性區位移及特征曲線新解，并對其進行分析與比較驗證.文獻[15]比較全面地分析了圍巖與支護的相互作用，并對不同變形階段圍巖與支護作用機制進行了更加進一步解析.

然而，以上研究者的研究均以隧道開挖前原巖狀態為彈性狀態，開挖后從隧道壁面開始依次形成不同塑性區和彈性區的圍巖為研究對象，未考慮一些特殊的隧道巖體.自重和地質構造運動作用下，埋深大且多次發生構造運動的地帶會形成塑性巖體，這種塑性巖體在隧道開挖前原巖已經為塑性狀態.巖體在低地應力條件下多表現出明顯的脆性，而在高地應力條件下塑性表現更明顯，由于巖體節理面所引起的各向異性也減弱.對平面應變假設條件下高地應力軟巖圓形隧道軸對稱彈塑性分析是隧道支護設計的重要內容.鑒于此，本文主要研究特殊的塑性巖隧道，即隧道開挖前隧道設計線路范圍的原巖就已處在塑性狀態，隧道開挖后對支護有影響的圍巖全部在塑性區范圍內，考慮塑性軟巖的軟化模型，依據塑性力學求解塑性巖隧道的應力場，較系統地研究塑性巖隧道的圍巖破壞區及隨塑性區形態的變化對應的塑性形變壓力的問題，為深部塑性巖隧道的支護設計提供一定的理論依據.

1 圓形塑性軟巖隧道的應變軟化模型

1.1 基本假定

1) 假定隧道截面為圓形，圍巖為均勻連續介質.

2) 側壓力系數λ=1，支護力pi環向均勻分布.

3) 考慮為平面應變問題進行分析.

4) 不考慮圍巖自重，且埋深大于20倍隧道半徑.

5) 開挖前巖體處于理想的塑性狀態.

1.2 開挖后塑性巖圓形隧道的力學模型

圓形隧道開挖后考慮應變軟化的圍巖力學模型如圖1所示.隧道半徑為a，無限遠處受到均勻地應力p0的作用，在洞壁處受到支護結構的支護力pi.開挖后假設形成了半徑為rf的塑性殘余區、半徑為rs塑性軟化區和半徑為rd的塑性擾動區，軟化區以外為理想塑性區.

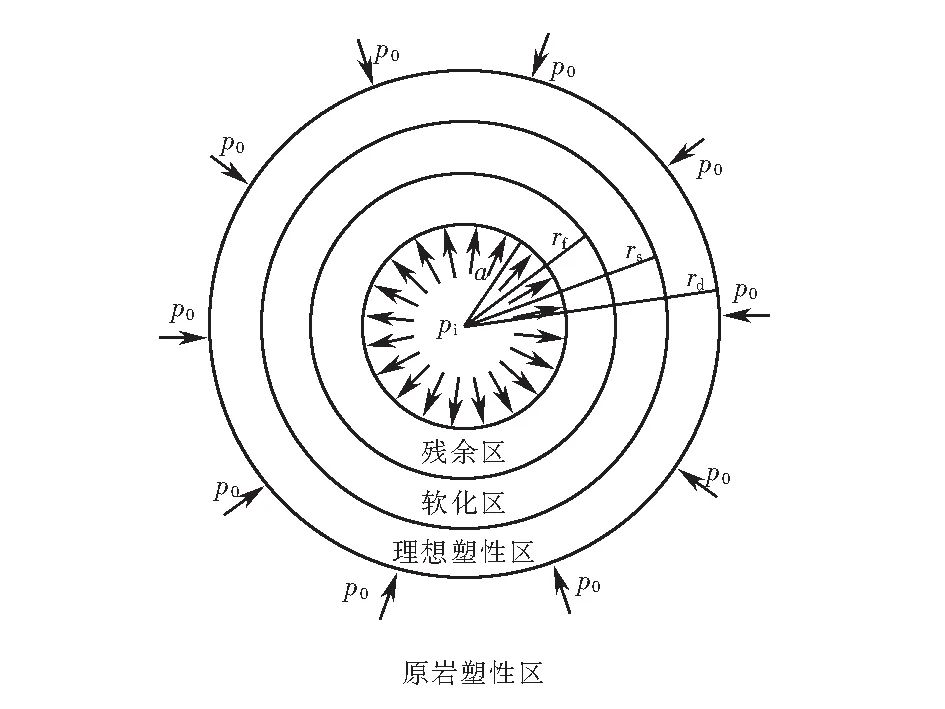
圖1 應變軟化圍巖的力學模型Fig.1 Mechanical model of strain-softening rock mass

1.3 圍巖軟化模型及軟化模量

巖體的力學性能一般由巖體中節理、斷層、層理等結構面決定.室內的巖樣試驗由于體積小，且脫離了現場巖體的地質力學特性，因而不能充分地反映巖體力學特性，而巖體現場試驗能較為全面地反映出巖體力學特性. 課題組參與的鐵道部科技研究開發計劃重大課題中，對蘭渝鐵路毛羽山隧道Ⅳ級軟巖段和木寨嶺隧道高地應力Ⅴ級軟巖段取樣進行了現場直剪試驗，其現場直剪試驗曲線如圖2～3所示.兩座隧道各取一組5個試樣，依次按法向應力的大小編號為試件1、試件2、試件3、試件4、試件5(其中毛羽山隧道中的3號試件在加工時受裂隙發育碎裂影響，試件長度和寬度較其他4個試件各少了5 cm).

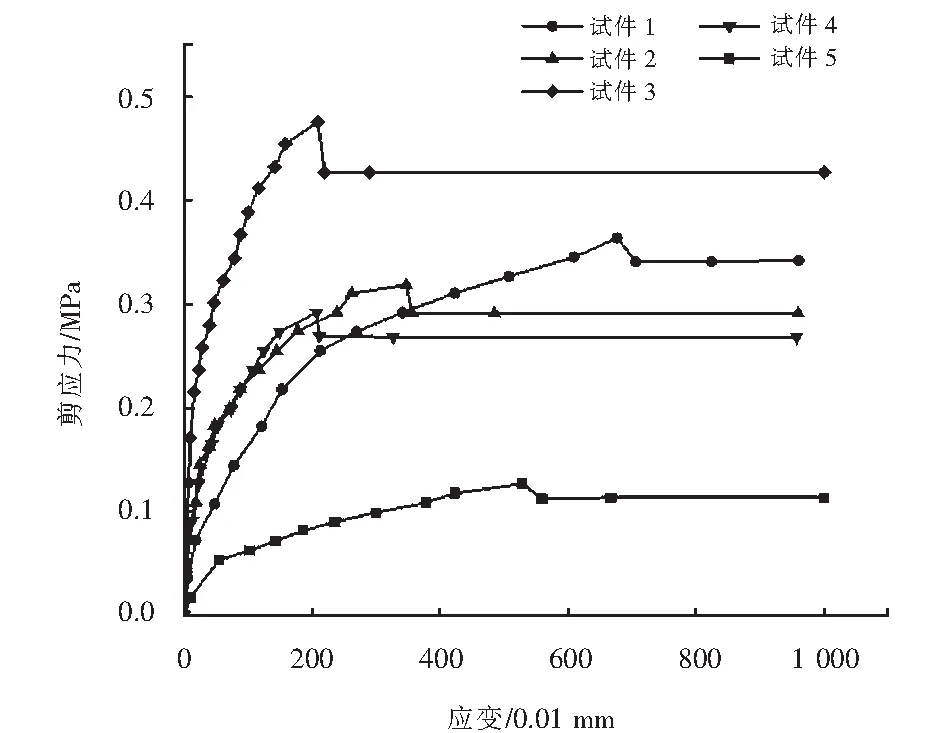
圖2 毛羽山隧道塑性軟巖現場直剪試驗曲線Fig.2 Field shear test curve of plastic soft rock in Maoyushan tunnel

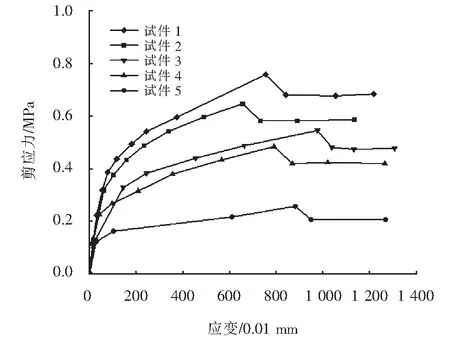
圖3 木寨嶺隧道塑性軟巖現場直剪試驗曲線Fig.3 Field shear test curve of plastic soft rock in Muzhailing tunnel

從兩組試驗看到，整個剪應力-應變曲線形式為不規則的拋物線，兩組試驗所在試驗段巖體都是高地應力軟巖，在現場直剪試驗的整個過程中，剪斷面持續地發展、貫通，試件不斷的發生蠕滑，直至試件破壞，剪斷面上沒有應力集中表現，說明巖體破壞形式是以塑性破壞為主.從本次試驗同時進行的巖體的變形試驗正應力σ-應變ε關系曲線回滯環很小，巖體變形中不可逆變形很大，回彈變形很小，亦表明變形以塑性變形為主.且根據毛羽山隧道最大埋深約700 m，隧道區域最大水平主應力近22 MPa，圍巖強度應力比σc/σh,max=1.41，屬于極高地應力狀態，這些均說明以上的關系曲線能代表隧道設計線路范圍原巖為塑性狀態，且塑性變形顯著的地質軟巖應力-應變關系.

故根據以上現場試驗，并考慮到試驗開始段的試驗誤差等原因去掉試驗曲線一開始的上升段，塑性巖段隧道圍巖的塑性軟化應力τ-ε應變關系可以簡化為如圖4所示模型.隨著隧道開挖，圍巖應力逐步進行重新分布，繼而從隧道壁往外依次形成如圖1所示的分區，其中圖1中的塑性殘余區、塑性軟化區和理想塑性區，分別對應于圖4中ε>ε*直線段、εp<ε<ε*曲線段和ε<εp直線段.

圖4 塑性軟巖巖體軟化模型Fig.4 Plastic soft rock mass softening model

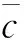
(1)

式中：c為峰值強度黏聚力；φ為峰值強度內摩擦角；c*為殘余強度黏聚力；φ*為殘余強度內摩擦角.

由上述畫出c、φ的變化規律如圖5～6所示.由于φ(ε)隨ε的增大損失量較少，故其直線斜率很小.

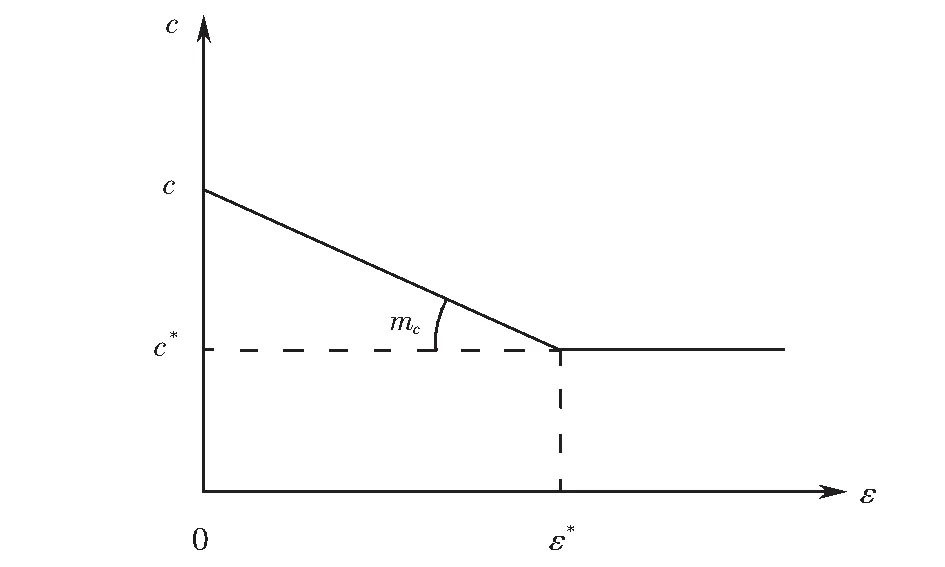
圖5 塑性軟巖巖體黏聚力的變化規律Fig.5 Change rule of cohesion of plastic soft rock mass

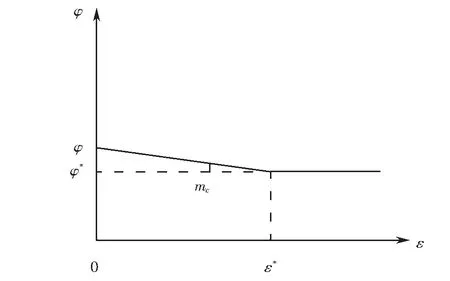
圖6 塑性軟巖巖體內摩擦角的變化規律Fig.6 Change rule of internal friction angle of plastic soft rock mass

2 隧道支護后的圍巖應力分析

根據前面1.2塑性巖隧道開挖后的力學模型，隧道開挖后洞壁巖體根據在最佳支護時間圍巖的變形破壞情況，將產生不同的塑性區，當隧道開挖后僅存在塑性軟化區和理想塑性區時，考慮到可以利用統計的方法求出巖石的強度，并分析試驗結果的可靠性，這里近似地采用Mohr-Coulomb直線型強度判據作為進入塑性狀態的條件，在塑性軟化區，應力關系滿足Mohr-Coulomb準則，即

(2)

式中：σ1為第一主應力；σ3為第三主應力.

根據圖(5)、圖(6)，在塑性軟化區內，c、φ隨塑性應變ε增大呈不同衰減，由式(1)可得：

(3)

(4)

根據彈塑性力學原理，對于塑性區中任意一點，應力分量滿足平衡條件，軸對稱問題不考慮體積力時，極坐標系中的應力平衡方程為

(5)

式中：r為圍巖中單元體距離隧道中心軸的距離；dr為單元體的厚度.

把塑性判據(4)式代入(5)式得：

(6)

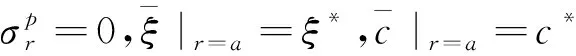
(7)

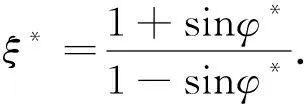
根據文獻[1]，隧道開挖應力擾動區范圍可由下式確定：

(8)

把(7)式代入(8)并化簡為

(9)

求解式(9)可得到擾動區半徑rd為

(10)

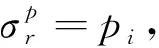
(11)

考慮到r=rd(擾動邊界區)時，把上式代入公式(8)可得：

(12)

從公式(12)求解得pi為

(13)

這里的支護阻力pi就是隧道開挖前隧道設計線路范圍的原巖為塑性狀態，隧道開挖后對支護有影響的圍巖全部在塑性區范圍內，沒有彈性區域的支護阻力.根據公式(13)，pi與初始地應力p0；巖體峰值強度時的巖性指標ξ、c；巖體殘余強度時的巖性指標ξ*、c*；擾動區半徑rd；隧道開挖半徑a均有關.當其他條件一定時，支護阻力pi隨著擾動區半徑rd的增大而減小.

3 隧道支護后的圍巖位移分析

當隧道開挖同時，支護結構立即施設并發揮作用，沒有時間差，且支護力足夠大，這時隧道壁位移u=0,但這實際是無法實現的，因為隧道開挖和支護結構發揮作用之間一定有一個時間差，且實際的支護結構也不是絕對地剛性，其與隧道圍巖的相互作用才形成支護阻力.這就會使隧道壁必然產生位移u>0，相應隧道直徑變小，u為隧道壁向隧道的徑向位移.擾動區邊界就是從隧道壁塑性區漸變到原巖狀態的邊界區域，在該邊界上巖體的性質發生了微小地改變，且可以恢復.故廣義上的擾動區半徑rd的范圍包括了塑性區和受開挖隧道影響的部分彈性區.根據文獻[16]，當考慮支護力pi作用時，在塑性應力狀態下，隧道壁位移為

(14)

考慮在塑性區邊界上，圍巖處在理想的塑性狀態，有：

(15)

將上式代入(11)式，整理計算可得：

(16)

把式(16)代入式(14)可得位移公式如下：

(17)

由公式(17)求出支護力pi為

(18)

該表達式直接體現出了支護力pi與變化的隧道壁徑向位移u之間的關系，同時考慮了圍巖參數在塑性軟化階段隨時空變化而變化的特性.從理論上講，把施工現場實測的隧道壁位移u與設計中預留的容許變形量進行比較，就可以確定實際需要的支護力pi.

4 結論

本文根據兩實際隧道工程軟巖段現場直剪試驗應力-應變曲線和部分常規三軸壓縮試驗應力-應變曲線，對圓形塑性軟巖隧道的應變軟化模型、支護后的應力狀態、位移狀態進行了研究，得到以下結論：

1) 通過對高地應力軟弱巖現場直剪試驗及其應力-應變關系曲線進行分析，得到了適用于塑性軟巖隧道的簡化了的應力-應變本構關系曲線.

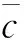
4) 建立了動態支護力pi與動態隧道壁徑向位移u之間的關系，該關系式很好地反映了新奧法中力學動態變化的理念.