基于自適應變分模態分解和包絡諧噪比的滾動軸承早期退化檢測

呂明珠， 劉世勛， 蘇曉明， 陳長征

(1.沈陽工業大學 機械工程學院，沈陽 110870；2.遼寧裝備制造職業技術學院 自控學院，沈陽 110161；3.中認(沈陽)北方實驗室有限公司，沈陽 110164)

滾動軸承是旋轉機械的主要部件之一，一旦發生故障會導致整機運行失效，因此對軸承進行狀態監測和故障預測具有重要的工程意義[1]。狀態監測的主要目的是判斷軸承的健康狀況，以便于及時處理已經發生或即將發生的故障，保證運行的可靠性和降低維修成本。

振動信號分析在滾動軸承狀態監測中應用最為普遍[2]。當發生局部故障時，振動信號會產生周期性的脈沖信號。然而，在早期故障階段，脈沖信號非常微弱且極易受到噪聲干擾，難以確定退化的起始點[3]。因此，振動信號處理技術和故障特征提取技術成為了早期故障診斷領域的研究熱點。

變分模態分解(variational mode decompositon，VMD)是一種于2014年提出的信號分析方法[4]，它能將信號分解為若干個具有一定帶寬和中心頻率的模態分量，而且能夠克服經驗模態分解(empirical mode decompositon，EMD)的模態混疊及集成經驗模態分解(ensemble empirical mode decompositon，EEMD)的時頻聚集性不高等問題。因此，近年來VMD方法在機械設備振動信號處理方面得到了廣泛的應用[5-7]。然而，在使用VMD進行信號分解之前，需要預先設置分解層數K和二次懲罰因子α等參數。Zheng等[8]采用觀察中心頻率法確定VMD的分解層數，這種方法需要有一定的經驗且很難快速準確地確定參數取值。任學平等[9]提出了用能量差曲線確定分解層數的方法，但需要對所有分解結果進行比較，計算量大且沒有考慮到懲罰因子對分解結果的影響。近年來一些傳統的優化算法如粒子群、遺傳算法、蟻群算法等開始逐漸應用于VMD的參數優化中，但普遍存在算法復雜、搜索速度慢、易于陷入局部最優等問題。灰狼優化算法(grey wolf optimization,GWO)是一種新型智能算法，具有較強的搜索能力和回避局部最優的特點[10]。因此，本文將GWO算法引入到VMD的參數選擇中，從而自適應地獲得最優參數組合，稱為自適應變分模態分解(adaptive variational mode decompositon，AVMD)。在早期故障特征提取方面，傳統的峭度指標對非周期干擾敏感，但隨著沖擊的密集這種敏感會逐漸失效。Chegini等[11]提出了一種新的特征提取方法，叫做包絡諧噪比(envelope harmonic-to-noise ratio,EHNR)，雖然能夠發現軸承早期故障異常點，但由于沒有很好地濾除干擾信號，造成在軸承運行初期出現誤報警(虛警)問題。

針對以上問題，本文提出了一種基于AVMD和EHNR的滾動軸承早期退化檢測方法。該方法包括信號處理和特征提取兩個步驟。在信號處理部分，先引入GWO算法優化VMD的參數選擇，再從VMD分解后的若干子模態中分理處有效模態分量并重構信號；在特征提取部分，利用EHNR劃分軸承全壽命運行的不同階段，通過設置報警閾值判斷是否出現異常點，實現了滾動軸承早期退化點的檢測且沒有出現虛警問題。實驗數據驗證了本文所提方法的有效性。

1 理論基礎

1.1 變分模態分解(VMD)

VMD是一種自適應、準正交且完全非遞歸的信號分解和時頻分布估計方法，它可以將輸入信號分解為若干個具有帶寬限制的本征模態函數(intrinsic mode function,IMF),并使每一組IMF集中在不同的中心頻率附近，具有良好的噪聲魯棒性。VMD方法的基本思路是將信號的分解過程轉化為變分問題求解，可以劃分為變分問題的構造和求解兩部分。

先對每個IMF分量做希爾伯特變換，具體如下

(1)

式中：δ(t)為脈沖函數；uk(t)是第k個IMF分量。

再將每個模態調制到相應的基頻帶，即將預估的中心頻率添加到每個IMF分量的分析信號中，如下所示

(2)

式中,ωk為每個分量估計的中心頻率。

通過求解調制信號梯度L2范數的平方構造如下約束變分問題

(3)

式中,f為原始輸入信號。

為了把約束變分問題轉化為無約束問題，引入了二次懲罰因子α和拉格朗日乘子λ(t)，得到擴展拉格朗日表達式

(4)

利用乘法算子交替方向法搜尋上述變分問題的最優解，得到uk、ωk及λ的更新公式為

(5)

(6)

(7)

式中：n為迭代次數；∧表示傅里葉變換；τ為噪聲容限系數。

迭代上述式(2)～(4)，直到滿足收斂條件

(8)

式中,ε為判別精度。

通常，在對信號進行VMD分解前需要人為地設定4個參數，分別為分解層數K，二次懲罰因子α，噪聲容限系數τ和判別精度ε，其中τ和ε對VMD分解結果影響不大，一般可采用默認值[12]。而K和α是決定VMD分解能否達到良好效果的兩個重要參數，若K值選擇不當會造成欠分解或過分解現象，若α值選擇不當會影響模態分量帶寬的大小，因此有必要尋找最優的參數組合。

1.2 灰狼優化算法(GWO)

GWO是一種新型智能搜索算法，具有原理簡單、搜索能力強、回避局部最優等優點，目前已被證明該算法與傳統的遺傳算法、粒子群算法和蟻群算法相比，在收斂精度和收斂速度方面更具優勢[13]。在GWO算法中，按照評估候選解的適應度優劣程度從高到低分為α,β,δ,ω4個等級，狼群的位置通過計算與獵物之間的距離不斷更新和進化，最終實現狩獵，具體操作如下

(1) 圍捕策略

D=|C·Xp(t)-X(t)|

(9)

X(t+1)=Xp(t)-A·D

(10)

C=2r1

(11)

A=2a·r2-a

(12)

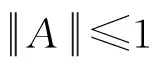
(2) 位置更新

Dk=|Ci·Xk(t)-X(t)|

(13)

Xi(t)=Xk(t)-Ai·Dk

(14)

(15)

式中：k=α,β,δ代表候選解評估排名前三的優質狼；i=1,2,3代表使用α,β,δ更新的其它個體狼；X(t+1)為迭代后狼群的位置。

2 所提方法

2.1 AVMD算法

由于分解層數K和二次懲罰因子α對VMD分解結果有顯著影響，若參數選擇不當會導致模態分量丟失或模態混疊現象[14]，因此本文將GWO算法引入VMD的參數優化過程，自適應地獲得最佳參數組合，解決了依賴經驗或先驗知識人為設定的問題。

適應度的選擇是優化算法的核心問題，由于包絡熵(envelope entropy,EE)可以反映信號的稀疏性，故障脈沖越規律則包絡熵越小[15]。因此，本文將最小平均包絡熵(minimum average envelope entropy,MAEE )為AVMD算法的目標函數，定義如下

(16)

(17)

(18)

根據前面的理論分析，AVMD算法的基本流程如圖1所示。

圖1 AVMD算法流程圖

2.2 有效加權稀疏峭度指標

利用AVMD算法可將原信號分解成K個IMF模態分量，這些分量有些包含了豐富的故障信息，有些則是噪聲干擾，為了便于分離，常采用峭度準則或相關系數準則進行識別[16]。然而，峭度雖然能反映沖擊信號的分布密度但忽略了振幅大、分布分散的分量；而相關系數雖然能表達分量對原信號的復現程度卻易受噪聲干擾，這說明單一的指標并不能完全詮釋信號的振動特性。因此，本文提出了一個新的評價指標——有效加權稀疏峭度指標(efficient weighted sparseness kurtosis index,EWSK),定義如下

WSK=Spa·Kur·Cor

(19)

(20)

(21)

(22)

(23)

按式(23)計算所得的EWSK大于0，則認為是有效模態分量，否則為噪聲模態分量。EWSK結合了稀疏度、峭度、相關系數的優點，使重構信號不僅保留了原始信號的故障信息而且有效地濾除了噪聲。

2.3 包絡諧噪比(EHNR)

EHNR是指對數據樣本做包絡處理后諧波能量與噪聲能量的比值，它的大小不僅可以表征故障的強弱，還可以充分反映故障引起的周期性沖擊，是一種用于滾動軸承故障診斷和預測的新指標。

(24)

(25)

(26)

(27)

式中,τ為自相關函數的時間滯后量。

確定原始信號的自相關函數在時間滯后域中的最大位置，即EHNR定義如下

(28)

式中：τmax為rx(τ)自相關函數的最大位置；rx(τmax)為最大位置對應的幅值；rx(0)為包絡總能量。

2.4 基于AVMD-EHNR的滾動軸承早期退化檢測方法

滾動軸承的全壽命運行周期通常可分為正常期、輕微退化、中度退化、嚴重退化和失效期5個階段，其中退化期是故障從產生到擴展的劣化過程，若能檢測到退化的起點，不僅有助于早期故障診斷防止缺陷進一步擴大，而且為剩余壽命預測機制的及時啟動提供依據，具有重要的工程意義和經濟價值。

AVMD-EHNR方法的實現過程如圖2所示。首先，將原始信號進行AVMD分解，采用EWSK指數從K個模態分量中選擇有效IMF分量并重構信號，然后計算重構信號的EHNR，由高斯分布的4σ準則[17]，設置報警閾值為正常期時相對穩定的EHNR均值μ加上4倍標準差σ，超出這個區間的數據則為異常點，根據報警閾值判斷軸承是否進入退化期，并找出退化的起始點，實現軸承早期退化檢測。

圖2 AVMD-EHNR實現過程

3 仿真驗證

通過構造一組仿真信號來驗證所提AVMD方法及EWSK指標的有效性，如式(29)所示

(29)

式中:x1(t)為低頻信號；x2(t)為間歇性信號，用來模擬故障脈沖；x3(t)為高頻信號；x4(t)為均值為0方差為0.1的隨機噪聲；仿真信號的采樣頻率為1 000 Hz，采樣點數為1 200，時間為1 s，如圖3所示。

圖3 仿真信號及其分量

首先，利用傳統的EMD和EEMD方法對原信號進行分解，各分量的時頻信息分別如圖4和圖5所示。從圖中可以看出，EMD和EEMD將原信號分別分解成7個分量和6個分量，都存在不同程度的模態混疊現象而且沒有分離出高頻分量并都有模態重復問題。

(a) 時域結果

(a) 時域結果

下面采用所提AVMD方法對原信號進行分解，設置GWO狼群數量為20，最大迭代次數為10。根據MAEE原則得到的K和α的最佳組合為〈3,1 556〉，再對原信號進行分解，如圖7所示。原信號被分解成中心頻率分別為42 Hz，113 Hz和250 Hz的3個分量，與原信號對比可以看出，不僅避免了模態混疊問題還濾除了噪聲分量，充分體現了AVMD方法的優越性。

接下來，利用所提的EWSK指標選擇有效IMF分量，如表1所示。為了驗證EWSK指標的有效性，表1中的前2行分別列出了各分量的峰值信噪比(peak signal to noise ratio,PSNR)和均方誤差(mean square error,MSE)，這是用來評價重構信號質量的常用指標，見文獻[15]。從表中可以看出，IMF2的PSNR最高(基準為30 dB，越高越好)且MSE最小，這說明該分量包含了豐富的故障信息和原信號的波形和頻譜中尖峰特征。同時，表1中還列出了各分量的EWSK計算結果，選擇其值大于0的IMF2為有效特征分量，而其值小于0的IMF1和IMF3為偽分量。

表1 有效IMF分量的選擇

然后，采用固定參數的VMD方法對原信號進行分解，選擇K和α分別為4和2 000，分解結果如圖6所示。從圖6中可以看出，由于沒有合理選擇VMD的參數，不僅出現了過分解問題，且原信號中的3個中心頻率也沒有準確提取出來。

(a) 時域結果

(a) 時域結果

由于所提EWSK準則憑借故障呈現的統計特性及其值的正負便能準確分離出有效的IMF分量，無需故障特征的先驗知識，所以即使在缺乏故障精確信息的不利條件下也能很好地完成分離任務。

4 案例分析

4.1 滾動軸承全壽命實驗數據

本文使用的實驗數據來自辛辛那提大學智能維護中心(IMS)提供的滾動軸承全壽命數據集[18]，實驗裝置如圖8所示。

(a) 測試系統

電機轉速為2 000 r/min通過皮帶驅動軸轉動，軸上安裝了4個相同的ZA-2115型滾動軸承，施加26 690 N的徑向載荷，由PCB353B33型加速度傳感器收集振動信號，采樣頻率為20 kHz，每10 min采集1次。4個軸承均采用強制潤滑，通過磁塞從油循環中收集碎屑，當碎屑超過一定水平時，開關關閉實驗停止。數據集共有3個測試案例，表2記錄了失效軸承的編號及故障類型，全壽命振動數據如圖9所示。

表2 全壽命實驗案例簡要信息

(a) 案例1

4.2 振動信號處理

以案例2中的100個樣本數據為例，設置GWO的狼群數量為20，最大迭代次數為10，模態分量K的取值范圍為[2,12]，二次懲罰因子α的范圍為[1 000,3 000]。搜索結果如圖10所示，迭代了4次就已收斂，此時對應的K和α分別為6和2 048，并與K和α分別取4和2 000的固定參數VMD進行對比，如圖11所示。在圖11(a)中丟失了0～1 000 Hz和5 000～6 000 Hz范圍的模態，屬于欠分解。在圖11(b)中，模態分量在各頻帶分布均勻且沒有出現模態混疊現象，說明振動信號沒有被欠分解和過分解。再根據EWSK指標選擇IMF3和IMF4為有效IMF分量，如表3所示。重構信號的PSNR和MSE分別為73.139 2 dB和0.003 2，說明保留了大量原信號故障信息。

圖10 案例2的GWO收斂曲線

(a) 固定參數VMD分解后的頻率譜

表3 案例2每個模態分量的EWSK值

按照上述方法，分別對案例1和案例3中的數據進行處理，經GWO優化后得到的最優參數組合分別為〈6,2 078〉和〈6,2 114〉，選取有效分量分別為IMF3、4、5和IMF1、4，對有效分量進行信號重構，這樣既去除了噪聲干擾又保留了豐富的故障信息。

4.3 早期故障點檢測

為了驗證EHNR指標對軸承早期故障的敏感性，先對案例2中的軸承1的全壽命數據采用有效值和峭度指標分析，如圖12所示。從圖12中可以看出，有效值雖然能表征軸承退化過程的整體趨勢，但對早期故障并不敏感。而峭度指標對較大的干擾沖擊敏感，并隨著沖擊的密集這種敏感會逐漸失效，兩種指標都很難確定退化的起始點。

(a) 有效值指標

然后再根據所提EHNR指標進行分析，如圖13所示。從圖13(a)中可以明顯識別出軸承1從運行到失效的5個階段，這說明該指標趨勢性好。1為正常期，歷經的時間最長(約為89 h),這一階段軸承處于穩定運行狀態，EHNR的值僅有微小的波動，選擇這一時期EHNR的均值加上4倍標準差確定報警閾值，如圖13中紅線所示；2為輕度退化期，從EHNR超越報警閾值開始累計，此時的故障特征往往被強噪聲掩蓋，而首個認定的異常點即為故障的起點，如圖13(b)所示；3為中度退化期，是故障擴展階段，這一階段故障的尺寸會加深加大，故障特征也變得更加明顯，但也會由于連續的接觸磨損使故障部位變平滑，出現“自愈”的假象，EHNR的幅值出現先升高后降低的現象；4為嚴重退化期，此時軸承故障缺陷增長加快，EHNR幅值劇烈振蕩，工作的可靠度顯著降低，軸承瀕臨失效；5為失效期，此時軸承已完全不能可靠工作，甚至會對整個機械系統造成嚴重危害。

(a) 軸承運行狀態劃分

采用本文所提方法對原始信號進行分解和重構，再計算重構信號的EHNR，如圖14所示。

圖14 案例2的AVMD-EHNR方法檢測結果

從圖14中可以看出，AVMD-EHNR方法識別的異常點為第536個樣本點，比原始信號識別的547點早了11個樣本(約為1.8 h),雖然兩個結果中均沒有出現虛警點，但是明顯看出所提方法得到的EHNR幅值在運行前期更加平穩，整體振蕩不大。

采用同樣方法對案例1和案例3中的軸承3的全壽命數據進行分析對比，得到的結果如圖15和圖16所示，其中圖15(a)和圖16(a)分別表示原信號的檢測結果，圖15(b)和圖16(b)分別表示采用本文所提方法得到的檢測結果。再將本文所提AVMD-EHNR方法與文獻[11]所提的快速集成經驗模式分解(fast ensemble empirical mode decomposition,FEEMD)方法的檢測結果進行比較，如表4所示。

(a) 案例1原信號的檢測結果

(a) 案例3原信號的檢測結果

表4 三種方法的早期退化點檢測結果對比

結合圖15、圖16及表4可以看出，案例1的原始信號EHNR值在運行初期極不穩定，造成虛警率很高，FEEMD-EHNR方法雖然解決了原始信號的虛警問題，但是檢測結果卻比本文方法晚了105個樣本點(約為17.5 h)；案例3的原始信號EHNR值在運行初期有3處虛警點，而FEEMD-EHNR方法雖然將虛警點降為1個但檢測結果仍比本文方法晚(約為0.83 h)。經過對比發現，本文所提方法在3個案例的檢測中均沒有虛警問題，且檢測的早期故障點比原始信號和FEEMD-EHNR方法都要早，這說明AVMD-EHNR方法不僅可以有效濾除噪聲分量，而且可以更好地識別早期故障點，兼具魯棒性和敏感性，適合滾動軸承在線運行檢測和故障診斷。

5 結 論

為了檢測滾動軸承的早期故障點，提出了一種基于自適應變分模態分解(AVMD)和包絡諧噪比(EHNR)的方法。

(1) 采用GWO算法得到了VMD的最佳參數組合，解決了人為選擇參數困難及參數設置不當帶來的模態分量丟失和模態混疊問題。

(2) 提出了一種有效加權稀疏峭度指數(EWSK)，該指標可對故障模態分量和噪聲模態分量進行區分，從而獲得含噪少且故障信息豐富的重構信號。

(3) EHNR是一種新的故障特征提取技術，與傳統的有效值和峭度指標相比，它對周期性故障脈沖具有更強的敏感性、魯棒性和趨勢性。

(4) 結合AVMD和EHNR的優點對重構信號進行分析，可以剔除運行初期的虛假異常點，有效避免“虛警”現象，有利于進一步識別出真實的異常點，從而解決了軸承退化過程的起始點難以確定的問題，為滾動軸承早期故障診斷和剩余壽命預測提供依據，有重要的工程意義。