局部完全環的同調刻畫

林詩雨， 王芳貴， 陳 丹

（四川師范大學 數學科學學院，四川 成都610066）

本文恒設R是有單位元的交換環.pdRM和fdRM分別表示M的投射維數和平坦維數，gl.dim（R）和w.gl.dim（R）分別表示環R的整體維數和弱整體維數，FPD（R）表示環R的finitistic投射維數.

設M是R-模.稱M是Max模，是指M的每個非零子模都有一個極大子模.稱環R是Max環，是指所有非零R-模都是Max模.文獻［1］對半素環進行同調刻畫時，證明左完全環是左Max環.文獻［2-5］進一步證明環R是Max環當且僅當它是一個局部完全環，當且僅當對任何p∈Max（R）有Rp是Max環.文獻［6-7］從范疇的角度對Max環進行了等價刻畫.文獻［8］證明了R是一個局部完全環，當且僅當對任意R-模C有（F，C）＝0，其中F是一個循環平坦模.文獻［9］用“投射下降法”對局部完全環進行了刻畫.文獻［10］用幾乎投射模對局部完全環進行了刻畫.M是一個幾乎投射模.是指對任意的Rm-模N有（M，N）＝0，其中m∈Max（R）.環R是局部完全環當且僅當平坦模是幾乎投射模.這時有FPD（Rm）＝0，其中m∈Max（R）.

文獻［10］定義了模M的幾乎投射維數和環R的幾乎整體維數，分別用ApdRM和a.gl.dim（R）表示.若a.gl.dim（R）＝0，則R是von Neumann正則環.若a.gl.dim（R）＝1，則R是almost Dedekind整環.對R-模M，有

對環R，有

本文在文獻［10］的研究基礎上，對幾乎投射模及幾乎投射維數做了進一步的刻畫.建立了商環上的幾乎投射維數和滿射情況下幾乎整體維數的換環定理.在定義了環R的幾乎finitistic投射維數AFPD（R）的基礎上，證明

AFPD（R）≤Sup｛FPD（Rm）｜m∈Max（R）｝.指出了若環R是局部完全環，則AFPD（R）＝0.最后，證明了整環R是局部幾乎完全整環當且僅當對R的任何極大理想m，有Rm是幾乎完全整環.

1 幾乎投射模與幾乎投射維數

以下總用A P表示幾乎投射模類.

命題1.1對模P，以下各條等價：

1）P是幾乎投射模；

2）設0→A→B→P→0是正合列，m∈Max（R），則對任意的Rm-模N，有正合列

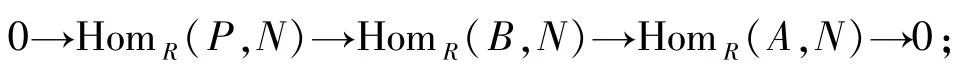
3）設A是B的子模，m∈Max（R）.對任意的Rm-模N，若B／A?P，則任何同態 ψ：A→N都可以擴張到B；

4）設m∈Max（R），N是Rm-模，則任意正合列0→N→B→P→0都是分裂的.

證明1）?2） 由正合列

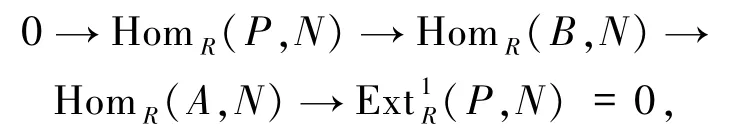
即證.

2）?3） 設0→A→B→B／A→0是正合列.已知B／A?P，由2）可以得到

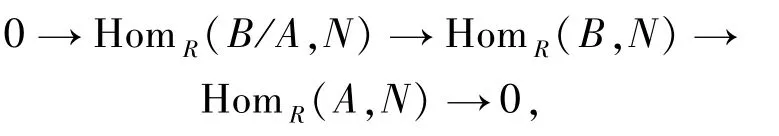
即任何同態ψ：A→N都可以擴張到B.

3）?4） 設0→N→B→P→0是正合列，且B／N?P.由3）知 ψ：N→N可以擴張到B，所以正合列0→N→B→P→0是分裂的.

4）?1） 由題設，N到P的擴張是分裂的.再由文獻［11］的定理7.20，有（P，N）＝0，故P是幾乎投射模.

命題1.2設I是R的一個理想，＝R／I.若P是幾乎投射R-模，則P／IP是幾乎投射-模.

證明設P是一個幾乎投射R-模.I是R的一個理想，＝R／I.若N是R／I的極大理想，則存在R的一個極大理想M，使得I?M，且N＝M／I.由易知

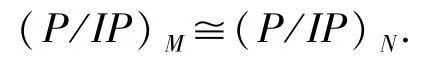
由同構（P／IP）N?（P／IP）M?P M／IPM和文獻［10］的定理2.3，有P M是自由的RM-模，故P M／IPM是自由N-模，即P／IP是幾乎投射-模.

命題1.3設S是R的乘法封閉集.若P是幾乎投射R-模，則P S是幾乎投射RS-模.

證明設M是RS的極大理想，則存在R的素理想m，使得M＝m S.由條件，Pm是自由Rm-模.設T是形如的元素的集合，其中s∈S，t∈R，t?m.則T是RS的乘法集，且有（P S）M＝（P m）T.故（PS）M是自由（RS）M模.因此，MS是幾乎投射RS-模.

定義1.4設M是R-模.若M有如下形式的幾乎投射分解

則稱M有有限的幾乎投射維數，其中M最短的幾乎投射分解的長度稱為M的幾乎投射維數，用ApdRM表示.若M沒有有限長度的幾乎投射分解，則記ApdRM＝∞.

例1.5設P是幾乎投射模，則0→P→P→0是P的幾乎投射分解，從而ApdR P＝0.反之，若ApdRP＝0，則P是幾乎投射模.

命題1.6設n≥0.對模M，以下各條等價：

1）ApdRM≤n；

2）設m∈Max（R），對任意Rm-模N，與任何k≥1，有（M，N）＝0；

3）設m∈Max（R），對任意Rm-模N，有

4）若0→Pn→Pn－1→Pn－2→…→P1→P0→M→0是正合列，其中P0，P1…Pn－1是幾乎投射模，則Pn也是幾乎投射模.

證明1）?2） 由于ApdRM≤n，故M有幾乎投射分解

由文獻［12］的定理3.3.2，有

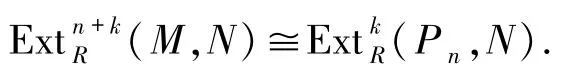
又由文獻［10］的命題2.4，可以得到

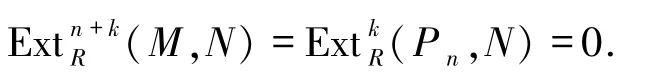
3）?4） 由文獻［12］的定理3.3.2，有

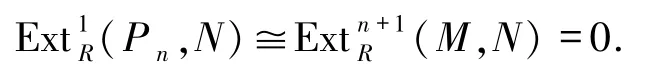
又由題設有m∈Max（R），N是Rm-模，由此可得Pn是一個幾乎投射模.

4）?1） 設…→Pn→Pn－1→Pn－2→…→P1→P0→M→0是M的任意幾乎投射分解.令An－1＝Ker（Pn－1→Pn－2），則0→An－1→Pn－1→P n－2→…→P1→P0→M→0是正合列.由假設，An－1是幾乎投射模，故ApdRM≤n.

推論1.7設ApdRM＝n≥0，m∈Max（R），則存在自由Rm-模F，使得（M，F）≠0.

證明設m∈Max（R）.根據命題1.6，對任意的Rm-模X，有（M，X）＝0，且有Rm-模N，使得（M，N）≠0.取自由Rm-模F及正合列0→A→F→N→0，則有

推論1.8設0→A→P→M→0是正合列，P是幾乎投射R模.若ApdRM＝n＞0，則ApdRA＝n－1.

證明設0→P n→P n－1→P n－2→…→P1→A→0是正合列，其中Pn－1，…，P1是幾乎投射模.因此，有正合列

由命題1.6，Pn是幾乎投射模，故ApdRA≤n－1.若n＝1，則A是一個幾乎投射模，則有ApdRA＝0＝n－1.現設n＞1，由于ApdRM＝n，故存在Rm-模N，使得（M，N）≠0，其中m∈Max（R）.由正合列（A，N）→（M，N）→（P，N）＝0知（A，N）≠0，故ApdRA≥n－1，由此得到

定理1.9設0→A→B→C→0是正合列.

1）ApdRC≤1＋Max｛ApdRA，ApdRB｝；

2）若ApdRA≤ApdRC，則

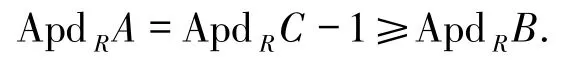
證明1）不妨設上式右端是有限值.設ApdRA≤n，ApdRB≤n，m∈Max（R）.對任何Rm-模N，有正合列

2）設ApdRB＝n，m∈Max（R）.當k＞n時，對任何Rm-模N，有正合列

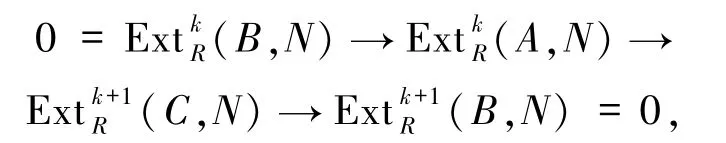
設ApdRA＝s，ApdRC＝m，m∈Max（R）.對任何Rm-模N，有（A，N）?（C，N）＝0，從而有m≤s＋1.另一方面，由于

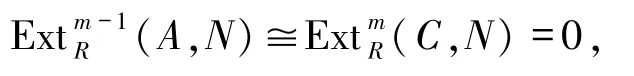
故s≤m－1.因此，可以得到m＝s＋1.

定理1.10設A是R-模，則

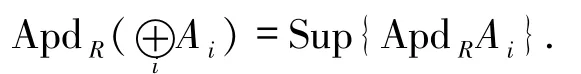
證明設m∈Max（R），記＝A.對任何Rm-模N，由于

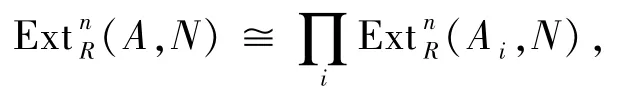
因此，結論成立.

定理1.111）A P關于直和與直和加項是封閉的.

2）A P關于滿同態的核是封閉的.

證明1）設｛P i｝是一簇R-模，m∈Max（R），M是Rm-模.由自然同構

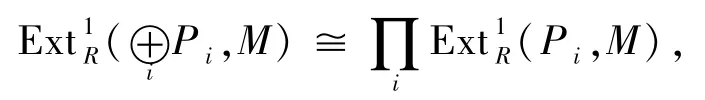
2）設0→A→B→C→0是正合列，其中C是幾乎投射模.設m∈Max（R），M是Rm-模.由命題1.6，對任何k＞0，有正合列

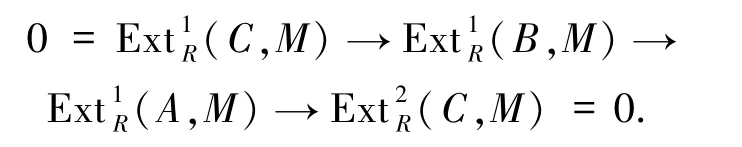
因此，有A是幾乎投射模當且僅當B是幾乎投射模.故A P關于滿同態的核是封閉的.

定義1.12對環R，令

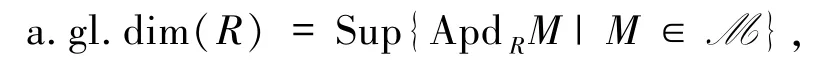
稱之為R的幾乎整體維數.

推論1.13設R是環，則a.gl.dim（R）＝Sup｛ApdR（R／I）｜I是R的一個理想｝.

證明對任意模M，由命題1.6，有ApdRM≤n當且僅當對任意的Rm-模N，（M，N）＝0成立，其中m∈Max（R）.這時idRN≤n.由文獻［12］的定理3.5.15有（R／I，N）＝0，其中I是R的理想，故有ApdR（R／I）≤n.

定理1.14設R是環，則

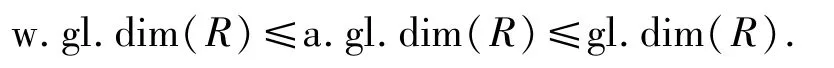
證明由文獻［10］的定理2.5，有fdR M≤ApdRM≤pdRM，即證.

定理1.15設R是完全環，則w.gl.dim（R）＝a.gl.dim（R）＝gl.dim（R）.

證明在完全環上，對任何的R-模M，有fdRM＝pdRM.根據定理1.14，此時結論顯然成立.

定理1.16設R是完全環.若a.gl.dim（R）＝0，則R是一個半單環.

證明由定理1.15，有

由題設a.gl.dim（R）＝0，有gl.dim（R）＝0，故R是半單環.

命題1.17對環R，以下各條等價：

1）a.gl.dim（R）＝0；

2）R是von Neumann正則環；

3）每個模都是幾乎投射模；

4）?m∈Max（R），Rm是域.

證明1）?2） a.gl.dim（R）＝0時，由定理1.14有w.gl.dim（R）＝0，故R是von Neumann正則環.

1）?3） 顯然.

2）?4） 由文獻［12］的定理3.6.16易知.

4）?3） 由題設，對任意R-模M，有Mm是自由Rm-模.根據文獻［10］的定理2.3，可以得到M是幾乎投射模.

命題1.18對整環R，以下各條等價：

1）a.gl.dim（R）≤1；

2）幾乎投射模的子模是幾乎投射模；

3）R的每個理想是幾乎投射模；

4）?m∈Max（R），Rm是一個離散賦值環；

5）?p∈Max（R），Rp是一個離散賦值環.

證明1）?2） 設M是一個幾乎投射模，L是M的子模.由正合列0→L→M→M／L→0，對任意的Rm-模N，其中m∈Max（R），有

2）?3） 顯然.

3）?1） 設I是R的理想，由題設有ApdRR／I≤1.又由推論1.13，a.gl.dim（R）≤1.

1）?4） 若a.gl.dim（R）≤1，根據定理1.14，有w.gl.dim（R）≤1.由文獻［12］的定理3.7.21，可知Rm是賦值環，其中m∈Max（R）.又由文獻［10］的定理3.6，有a.gl.dim（R）＝Sup｛gl.dim（Rm｜m∈Max（R）｝，有gl.dim（Rm）≤1，故Rm為Dedekind整環.由文獻［12］的定理3.7.20，易知Rm是一個局部整環.又由文獻［12］的定理5.2.14，有Rm是離散賦值環.

4）?1） 由題設有gl.dim（Rm）≤1，由文獻［10］的定理3.6，有

易知a.gl.dim（R）≤1.

4）?5） 顯然.

定理1.19設R是整環.若a.gl.dim（R）≤1，則R是一個凝聚環.

證明a.gl.dim（R）≤1時，由定理1.14有w.gl.dim（R）≤1，故R是一個Prüfer整環，即證R是一個凝聚環.

2 換環定理

引理2.1設φ：R→T是滿同態，對任何T-模M，有

證明設 φ：R→T是滿射，I＝Ker（φ）.不難得到T?R／I.設ApdTM＝ApdR／IM＝n＜∞.

由文獻［10］的定理3.3，有

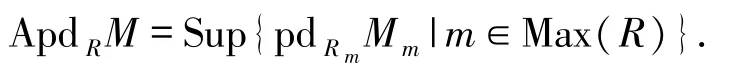
現證明

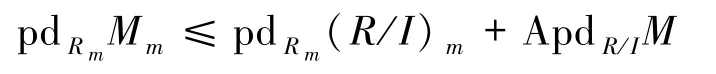
對?m∈Max（R）成立即可.

當n＝0時，若I?m，設

易知Mm?M.同理，（R／I）m?（R／I）.根據文獻［10］的定理 2.3，對?m∈Max（R／I），Mm是一個自由的（R／I）m-模，由此可得Mm?⊕（R／I）m.故Mm和（R／I）m作為Rm-模有Mm?⊕（R／I）m.由定理1.10，有

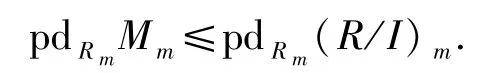
若Im，由（R／I）m＝0，有pdRm（R／I）m＝0.對

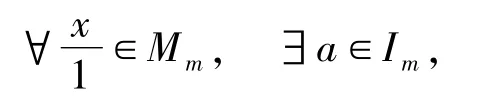
即證.

當n≥1時，取T-模正合列0→A→F→M→0，其中F是自由T-模.于是ApdTA＝n－1，故可歸納設ApdRA≤n－1＋ApdRT，又ApdRF＝ApdRT.因此，由定理1.9，有

綜上所述，

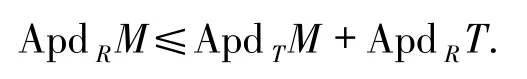
定理2.2設S是R的乘法集，L是RS-模，則

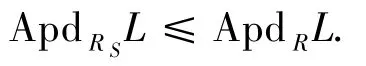
證明為證明ApdRSL≤ApdRL，不妨設ApdRL＝n＜∞，則有R-的幾乎投射分解

由命題1.3，每一個（Pi）S都是幾乎投射RS-模，從而

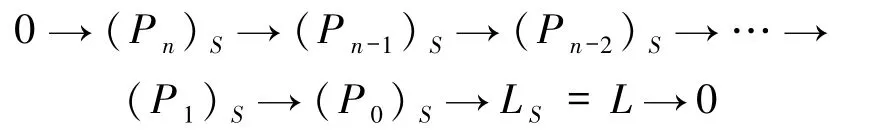
是L的RS-幾乎投射分解，故有ApdRSL≤n.

定理2.3設A是R-模，x∈R不是零因子，＝R／xR，則

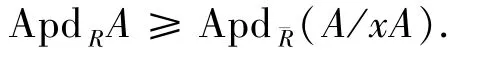
證明若ApdRA＝∞，則無需證明.不妨設

若A是幾乎投射R-模，由命題1.2有A／xA是幾乎投射-模，于是ApdRA＝Apd（A／xA）＝0，此時結論顯然成立.

若n≥1，設0→K→F→A→0是正合列，其中F是自由模.由定理1.8，有ApdRK＝n－1，故可歸納設Apd（K／xK）≤n－1.由題設，有正合列

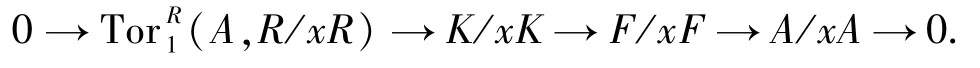
因為x是非零因子，故（A，R／xR）＝0.由定理1.9，可知

定理2.4設M是R-模，x∈R既不是零因子也不是單位，＝R／xR，Mx＝｛z∈M：xz＝0｝.

2）若ApdR M≤ ＋ ∞，則Apd（M／xM）和ApdMx同時有限.

證明不妨設ApdRM＝n＜∞.若ApdRM＝0，由命題1.2有ApdRM＝Apd（M／xM）＝0，易知此時還有Mx＝0，結論顯然成立.

考察正合列0→A→P→M→0，其中P是幾乎投射模，A是P的一個子模.由定理2.3有

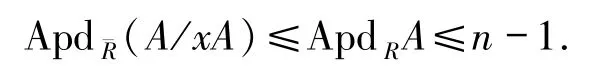
由題設，有正合列0→Mx→A／xA→P／xP→M／xM→0.令H＝Im（A／xA→P／xP），則有以下的正合列

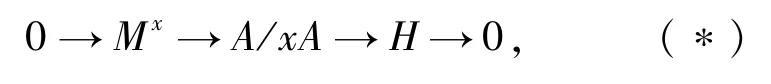
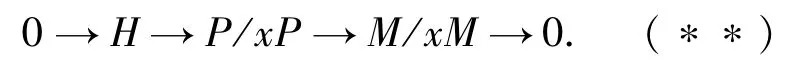
由（*），對任意的j≥0和任意的模B來說，有正合列

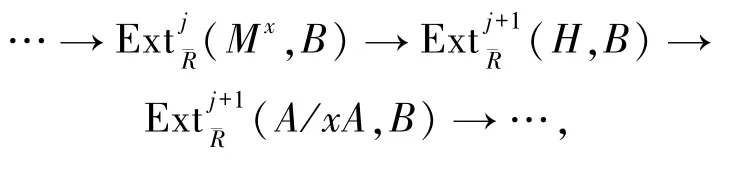
有

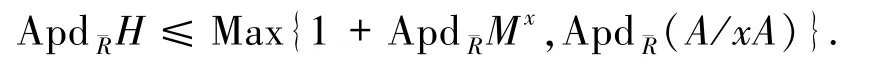
由（**）和定理1.9，有

于是

即證1）.

定理2.5設a∈R既不是零因子也不是單位，＝R／aR.

1）設A是非零的-模，若ApdA＜ ∞，則

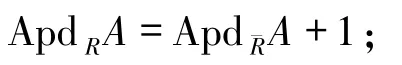
證明1）令ApdA＝n，由于a既不是零因子也不是單位，故＝1.由引理2.1，有ApdRA≤ApdA＋1＝n＋1.若n＝0，則ApdRA≤1.由于a不是零因子，故A不是幾乎投射模.現設n＞0.由文獻［14］的定理2.1和推論1.7，存在自由Rm-模F，使得

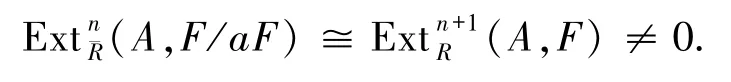
因此，有ApdRA≥n＋1，故ApdRA＝ApdA＋1.

3 局部完全環

定義3.1設R是環.令

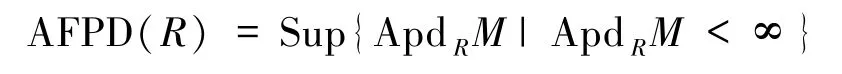
稱為R的幾乎finitistic投射維數.

命題3.2設R是環.

1）AFPD（R）≤a.gl.dim（R）；

2）若a.gl.dim（R）＜∞，則

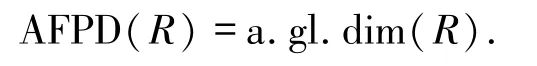
證明由定義1.12和定義3.1易證.

推論3.3設R是環，則AFPD（R）≤FPD（R）.

證明由文獻［10］的定理2.5，對任意R-模M，有ApdRM≤pdRM.于是

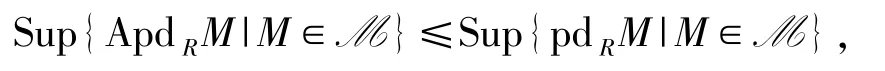
故AFPD（R）≤FPD（R）.

引理3.4設m∈Max（R），M和N是模，則（M，N）?（M，N）.

證明對任意的R-模P和Rm-模N，由文獻［13］的命題1.9，有

設0→A→F→M→0是正合列，其中F是自由R-模.考慮以下正合列構成的交換圖.

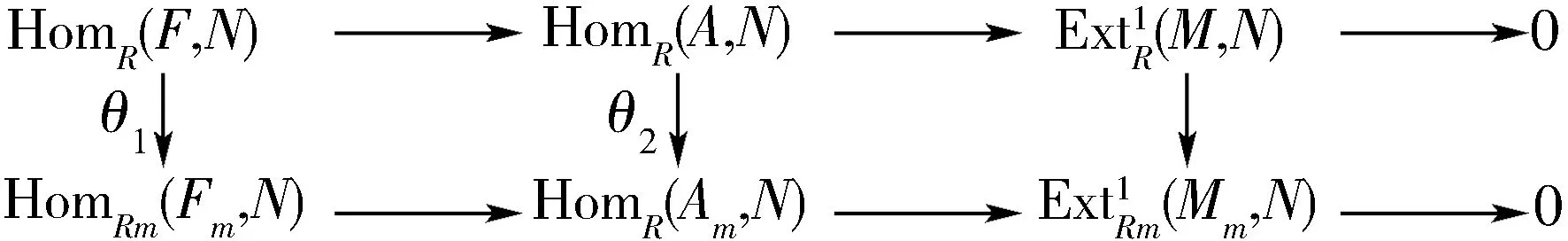
易知 θ1和 θ2是同構，于是

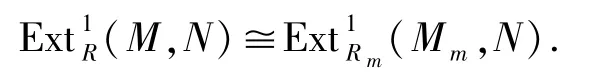
因為M是Rm-模，所以Mm＝M，故（M，N）?（M，N）.由維數提升可得

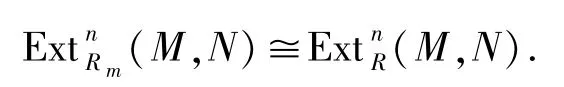
命題3.5設R是環，則

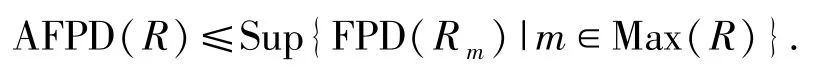
證明設Sup｛FPD（Rm）｜m∈Max（R）｝≤n，其中m∈Max（R）.對任意的Rm-模N有pdRm N≤n.由引理3.4，可知ApdRN≤n.由此可得

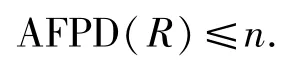
定理3.6設R是局部完全環，則AFPD（R）＝0.

證明設m∈Max（R），于是Rm是完全環.由文獻［2］的定理3.10.25，有FPD（Rm）＝0.又由命題3.5，有

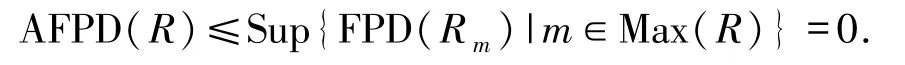
命題3.7設I是R的一個理想，＝R／I.若R是局部完全環，則R／I是局部完全環.

證明M是R／I的極大理想，則存在R的極大理想m，使得I?m，M＝m／I.由條件有Rm是完全環，根據同構（R／I）M?（R／I）m?Rm／Im和文獻［12］的定理3.10.23，有（R／I）M是完全環，故R／I是局部完全環.

設R是整環.若R的任何非平凡商環都是完全環，則R稱之為幾乎完全整環.文獻［15-16］對幾乎完全整環進行了系統刻畫.文獻［12］證明了整環R是幾乎完全整環當且僅當R有有限特征（即任何非零元素u只包含在有限個極大理想中，且對R的任何極大理想m，Rm是幾乎完全整環.）

定義3.8整環R被稱為局部幾乎完全整環，是指對R的任何非平凡商環是局部完全環.

定義3.9設R是局部幾乎完全整環.對任何非零元素u∈R，有AFPD（R／（u））＝0.

證明設R是局部幾乎完全整環，由定義3.8可知結論顯然成立.

定義3.10設AFPD（R）≤1，則對任何非零元素u∈R，AFPD（R／（u））＝0.

證明設A是任何非零＝R／（u）-模，ApdA＜ ∞.由定理2.5，ApdRA＝ApdA＋1≤1，故ApdA＝0.于是AFPD（）＝0.

定義3.11環R是局部幾乎完全整環當且僅當對R的任何極大理想m，有Rm是幾乎完全整環.

證明設R是局部幾乎完全整環，I是R的非零理想，M是R／I的極大理想，則存在R的極大理想m，使得I?m，M＝m／I.由（R／I）M?（R／I）m?Rm／Im，可知Rm／Im是一個完全環，故Rm是幾乎完全整環.

設Rm是幾乎完全整環，I是R的非零理想.M是R／I的極大理想，則存在R的極大理想m，使得I?m，M＝m／I.由（R／I）M?（R／I）m?Rm／Im，可知（R／I）M是一個完全環，故有R／I是局部完全環，即證R是局部幾乎完全整環.