n-余撓同調維數

熊 濤， 王芳貴， 王 茜

（1.西華師范大學 數學與信息學院，四川 南充637002； 2.四川師范大學 數學科學學院，四川 成都610066；3.四川文理學院 數學學院，四川 達州635000）

本文恒設R是給定的環，對左R-模N，

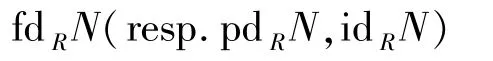
代表N的平坦（resp.投射，內射）維數.用Fn表示平坦維數不超過n的R-模簇，用

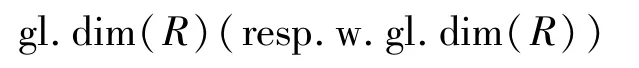
表示R的整體（resp.弱整體）維數.對于未解釋的概念和符號，參考文獻［1-2］.

模類＝｛W∈M｜對任意左R-模M∈Fn，都有（M，W）＝0.｝一直備受關注.Bass［3］證明了每個（左）R-模有投射蓋當且僅當R是左完全環（等價地，每個平坦R-模是投射模）.隨著蓋包理論的發展，Enochs［4］提出了平坦蓋猜測（flat cover conjecture，FCC）：每個R-模有平坦蓋.此后，多篇文獻討論了平坦蓋的存在性［5-7］.2001年，借助于模簇（學者們稱之為余撓模），Bican等［8］解決了“FCC”，即證明了結合環上每個模都有平坦覆蓋和余撓包絡.

按照同調理論的觀點，Mao等［9］定義了模M的余撓維數cotR M和環R的余撓整體維數l.cot.dim.（R），并且證明了環R是左完全環當且僅當

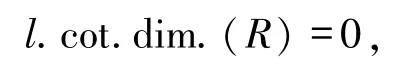
文獻［9］的推論7.2.7稱環R是左完全環是指每個R-模都有投射蓋.R稱為左m-perfect［10］是指每個平坦模的投射維數不超過m，由文獻［9］的推論7.2.6可知環R是左m-perfect當且僅當

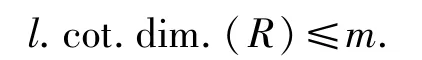
回顧交換環R稱為幾乎完全環是指它的每個真商環是完全環.幾乎完全整環（almost perfect domains），簡稱為APD.作為余撓模理論的推進，Lee［11］將整環上的稱為弱內射模.Fuchs等［12］定義了整環上的模的弱內射維數和環的弱內射整體維數，并在文獻［11］的引理3.6和文獻［12］的推論6.4中證明了一個整環是APD當且僅當它的弱內射整體維數≤1.Salce［13］證明了一個幾乎完全環或者是完全環，或者是APD.此外，沒有找到關于整體弱內射維數為零的相關環的表述.Mao等［14］研究了任意環上的，并將其稱之為n-余撓模.這實際上是對余撓模的進一步發展.借助n-余撓模，文獻［14］的推論6.4刻畫了環R的弱整體維數，證明了w.gl.dim（R）≤n當且僅當每個n-余撓模是內射的.Enochs等［15］借助1-余撓模刻畫了Noether環，文獻［15］的定理4.4證明了左右Noether環R的內射包E（R）是平坦模當且僅當每個1-余撓模M的平坦蓋F（M）是內射的.此外，Mao等［16］定義了另外一種n-余撓模：R-模N稱為n-余撓模是指對任意平坦R-模F，都有

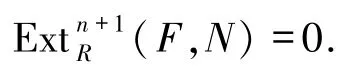
這2個概念是不一樣的，見例1.

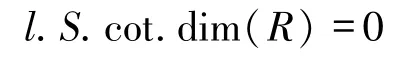
當且僅當

Vasconcelos［20］證明了一個交換環R是完全的當且僅當FPD（R）＝0.

上述事實表明，R的l.FPD（R）維數與一種廣義的-內射整體維數有著密切的聯系，尤其是l.FPD（R）維數下的一維環和一維整環，從已有的研究結果來看，這種關系似乎更加密切.本文正是基于這種思想展開討論的.

1 n-余撓模與n-余撓維數

容易看到，2種0-余撓模的定義是完全一致的，也就是余撓模.當n≥1時，文獻［14-15］中定義的n-余撓模，都是文獻［16］中定義的n-余撓模.但反之未必成立.

例1取環R＝Z及模M＝R／（2）.由于

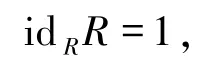
故R是文獻［16］中定義的1-余撓模.同時，運用文獻［21］的定理7.17可得到

以及

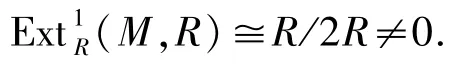
從而R不是文獻［14-15］中定義的1-余撓模.

下文提及的n-余撓模，均是指文獻［14-15］中定義的n-余撓模，并將該模簇記為Cn.

命題1對左R-模W，以下陳述是等價的：

1）W是n-余撓模；

2）對任意左R-模M∈Fn和任何整數k≥1，都有（M，W）＝0；

3）如果正合列0→W→B→C→0滿足C∈Fn，則它是分裂的；

4）如果正合列0→A→B→C→0滿足C∈Fn，則序列

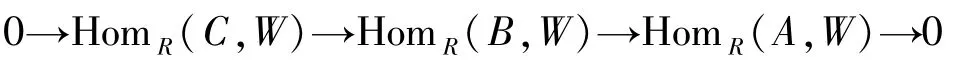
也是正合的.

證明1）?3）與2）?1）是顯然的，1）?4）參考文獻［14］命題4.4，下面只證1）?2）.由定義有現在假設k＞1.設0→A→F→M→0是正合列，這里F是投射左R-模，則

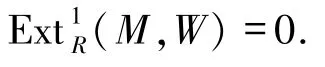
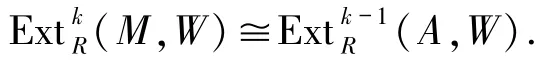
注意A∈Fn，故對k用歸納法，有

對R-模M的一個內射分解

記

則第n階上核Cn（n≥0）叫做M的第n階上合沖.

文獻［22］的定理2.2與文獻［23］的引理5.5證明了對于整環R，R-模M滿足fdRM≤1當且僅當對任意1-余撓模W，都有

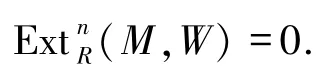
以下定理是對模的平坦維數的更寬泛的討論.

定理1設M是R-模.對任意n≥0，以下陳述是等價的：

1）fdRM≤n；

2）對任意0≤m≤n及任意m-余撓模N，成立；

3）對任意0≤m≤n及任意m-余撓模N及任意成立.

證明3）?2）是顯然的，令m＝n，由文獻［14］的定理3.4即可得2）?1）.下證1）?3）.設W是N的（n－m）階上合沖，由文獻［14］中的命題4.3可知，W是n-余撓.由命題1即得，對于任意

對任意的n≥0，都有Cn?Cn＋1.現在舉出一個滿足C0?C1?C2?…?Cn?…的環的例子.

例2取域F，構造環

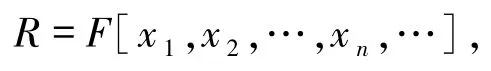
這里x1，x2，…，x n，…是F上的未定元，則R是凝聚整環.對任意n≥1，記J＝ （x1，x2，…，x n），則由文獻［24］的定理11.2.5可知

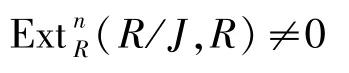
成立.設Cn－1是R的一個（n－1）階上合沖，再由文獻［24］中的定理11.2.5可知，Cn－1是（n－1）-余撓模，但不是n-余撓的.

定義1設M是R-模.M的n-余撓維數c nd RM是指使得序列這里對0≤i≤m，每個Wi是n-余撓模，是正合列的最小的非負整數m.如果不存在這樣的m，則記

環R的n-余撓整體維數l.Cn.D（R）定義為l.Cn.D（R）＝sup｛c ndRM｜M是任意R-模.｝.

現在給出模的n-余撓維數的等價刻畫.

定理2設m是非負整數.對R-模N，以下陳述等價：

1）c ndRN≤m；

2）對任意M∈Fn，

3）對任意M∈Fn和任意i≥1，

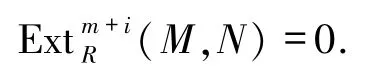
證明這是平凡的.

定理3設m是非負整數，則對環R，以下陳述等價：

1）l.Cn.D（R）≤m；

2）對任意的M∈Fn及N∈RM，

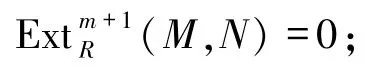
3）對任意的M，N∈Fn，

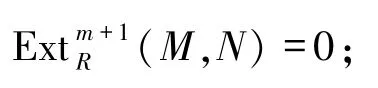
4）sup｛c ndRN｜N∈Fn｝≤m；

5）sup｛pdRM｜M∈Fn｝≤m.

證明5）?2）?3）是顯然的，由定理2即可得1）?2）與3）?4）.

4）?1） 設N∈RM，由文獻［14］中的定理3.4，可得正合列

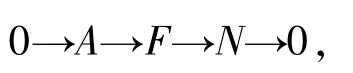
其中，F∈Fn，A∈Cn.對任意的左R-模M∈Fn，由命題1可得正合列

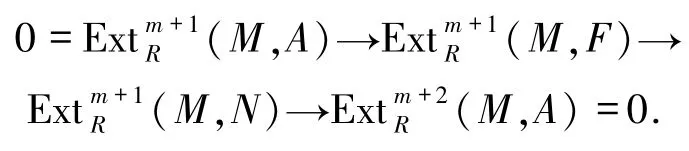
由定理2可得

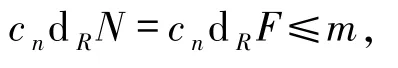
故

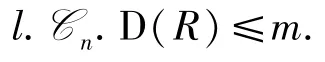
2 對環的刻畫

先來看什么時候每個n-余撓模是內射模.

定理4對環R，以下陳述等價：

1）w.gl.dim（R）≤n；

2）每個n-余撓模是內射的；

3）如果N∈Cn，則fdRN≤n；

4）對任意的M，W∈Cn，

成立.特別地，如果

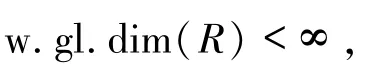
則上述各條還與以下陳述等價：

5）對任意的W∈Cn∩Fn，W是內射的.

證明1）?2） 由文獻［14］的推論6.4.

2）?4）和2）?5）是顯然的，由定理1即可得4）?3）.

3）?2） 設W是n-余撓模，且設

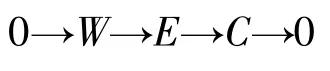
是正合列，這里E是內射模，則C是也是n-余撓的.由假設fdRC≤n，從而正合列是分裂的，故W是內射模.

5）?1） 用反證法.如果存在一個R-模滿足其平坦維數超過n，不妨假設存在一個R-模M滿足fdRM＝n＋1.由文獻［14］的定理3.4可知，存在正合列

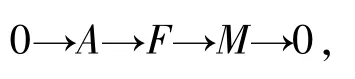
其中A是n-余撓的且滿足

則

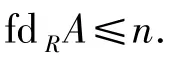
由假設，A是內射摸，從而給出的正合列是分裂的.因此，fdRM≤n.顯然，這是一個矛盾，從而

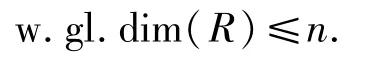
推論1對環R，以下陳述是等價的：

1）R是Von Neumann正則環；

2）每個余撓模N是內射模；

3）每個余撓模N是平坦模；

4）對任意的余撓模M和N，

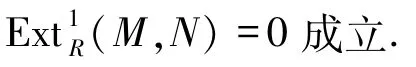
下面給出環R的l.Cn.D（R）維數與l.FPD（R）維數的關系.

定理5對任意環R，都有

特別地，如果

則對任意的

證明設l.FPD（R）＝k＜∞且M∈Fn.由文獻［25］中的命題6可知

故

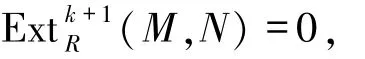
從而

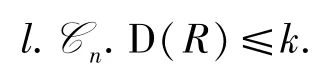
如果

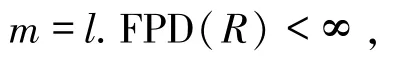
則存在一個R-模M滿足

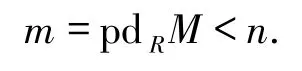
因此，存在一個R-模N滿足

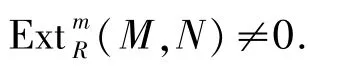
又因為M∈Fn和l.Cn.D（R）≥m，則

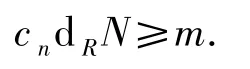
等價地，l.Cn.D（R）＝l.FPD（R）.

推論2設n≥1，R是環，有：

1）如果l.FPD（R）＝0，則每個R-模是n-余撓的；

2）交換環R是完全環當且僅當每個R-模是n-余撓的.

下面研究左完全環與l.FPD（R）維數的關系.文獻［3］定義了R的左弱finitistic維數：

引理1對環R，以下陳述是等價的：

1）l.FFD（R）≤n；

2）Fn＋1＝Fn；

3）Cn＋1＝Cn.

從而，l.FFD（R）＝0當且僅當每個余撓左R-模是1-余撓的.

證明1）?2）?3）是顯然，下面只證3）?1）.設M是R-模滿足

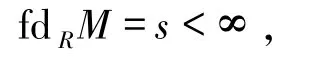
如果s＞n，不失一般性，假設s＝n＋1.由條件可知，對任意n-余撓模W，

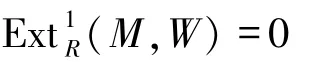
成立.由定理1可知

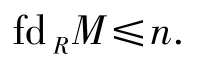
這是一個矛盾，故

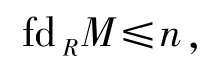
即

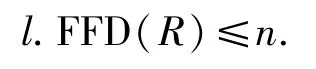
定理6設n≥1.對環R，以下陳述等價：

1）l.Cn.D（R）＝0，等價地，每個模是n-余撓模；

2）對任意模M∈Fn，M是投射的；

3）對任意模M∈Fn，M是n-余撓模；

4）R是左完全環且l.FFD（R）＝0；

5）l.FPD（R）＝0.

證明1）?2）?3） 運用定理3即可.而4）?5）是顯然的.

1）?4） 運用文獻［17］的命題3.3.1和引理1即可.

定義2稱環R為左Cn-遺傳環，即指：如果每個n-余撓模的商模是n-余撓的，等價于

定理7設n≥1，則對環R，以下陳述等價：

1）R是左Cn-遺傳環；

2）對任意模M∈Fn，pdRM≤1；

3）任意模M∈Fn，c ndRM≤1；

4）每個內射模的商模是n-余撓模；

5）對任意R-模M，E（M）／M是n-余撓模，這里E（M）是M的內射包；

6）對任意R-模M，E（M）／M是n-余撓模，這里E（M）是M的n-余撓包；

7）每個投射R-模P的子模N∈Fn－1是投射模.

證明1）?4）和1）?6）?5）是顯然的，而1）?2）?3）由定理3即得.

4）?1） 設0→N→W0→W1→0正合列，其中W0是n-余撓模.設E是W0的內射包.記

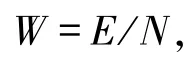
則可得如下行是正合列的交換圖

故

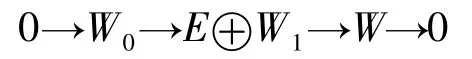
是正合的.對任意R-模N∈Fn，由假設可知

成立，故可由

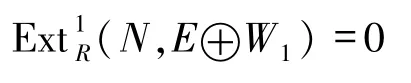
推出

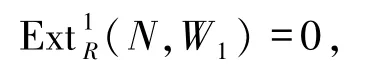
即W1是n-余撓的.

5）?4） 設0→K→E→C→0正合列，其中E是內射模.記E（K）?E是K的內射包，則存在R-模E0滿足

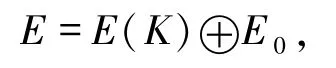
故

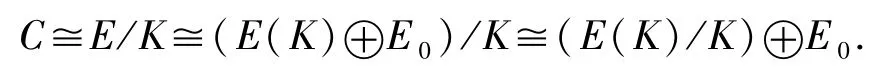
由假設可知，E（K）／K是n-余撓模，從而C是n-余撓模.

4）?7） 設P是投射R-模，N∈Fn－1是P的一個子模，且X是任意R-模，則存在正合列

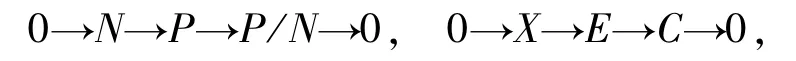
其中，P／N∈Fn，E是內射模.由假設可知，C是n-余撓.對任意α∈HomR（N，C），考察如下行是正合列的交換圖

則由命題1可知，存在 β∈HomR（P，C）滿足

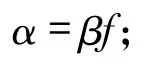
由于P是投射模，存在 γ∈HomR（P，E）滿足

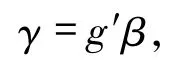
則

也滿足

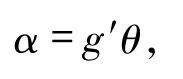
則

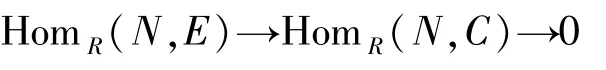
是正合列，則

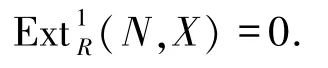
因此，N是投射模.

7）?1） 設W是n-余撓R-模，N是W的子模.對任意的A∈Fn，存在正合列0→K→P→A→0，其中P是投射模且K∈Fn－1.由假設，K是投射模.對任意的 α∈HomR（K，W／N），考察如下行是正合列的交換圖

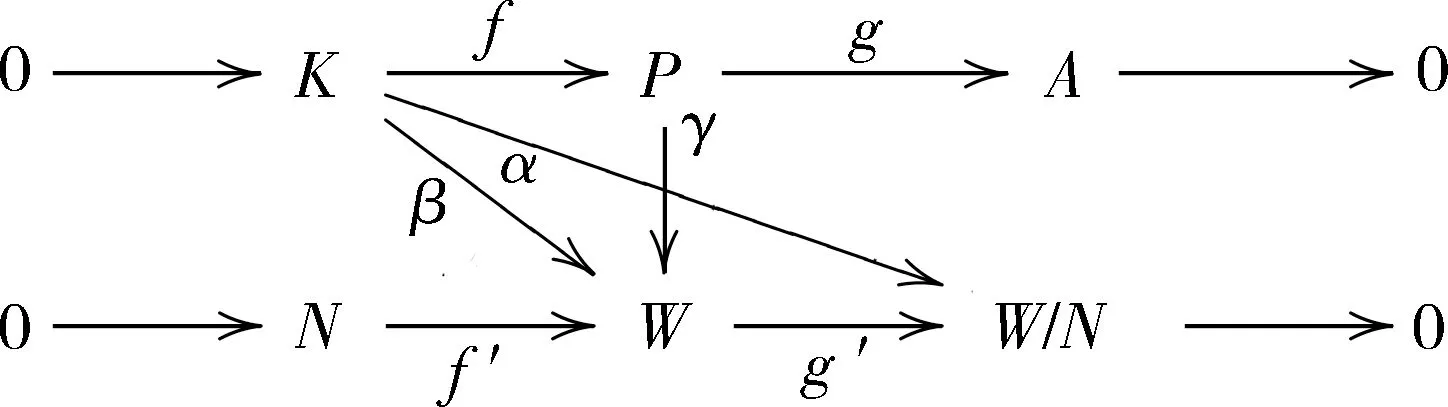
則存在同態

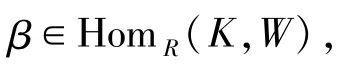
使得

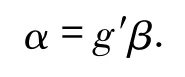
由假設可知，W是n-余撓模且A∈Fn，則由命題1可知，存在同態

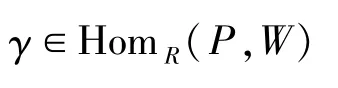
滿足

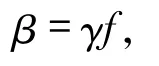
則

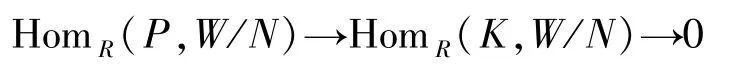
是正合列.由于

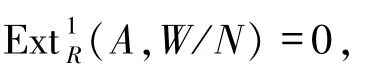
W／N是n-余撓模.

推論3對環R，以下陳述等價：

1）l.C1.D（R）≤1；

2）每個內射模的商模是1-余撓模；

3）每個投射模的平坦子模是投射的.

定理8設n＞1，R是環，則以下陳述等價：

1）l.Cn.D（R）≤1；

2）l.C2.D（R）≤1；

3）l.FPD（R）≤1；

4）l.C1.D（R）≤1且l.FFD（R）≤1.

證明1）?2） 顯然.

2）?3） 設M是R-模滿足k：＝pdRM＜∞.如果k＞1，則存在R-模N滿足pdRN＝2.由假設，pdRN≤1，這是一個矛盾，故k≤1.因此

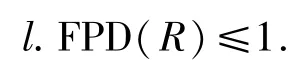
3）?4） 如果M∈F1，則存在正合列

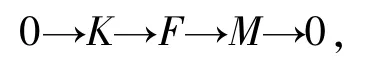
這里F是投射模，K是平坦模.由文獻［25］的命題6可知

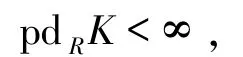
從而

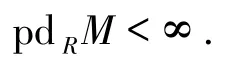
由假設，pdRM≤1，故K是投射模.因此

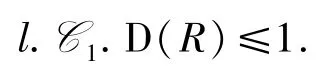
如果M∈F2，由定理7，fdRM≤pdRM≤1.因此，

故由引理1可得

4）?1） 由于l.FFD（R）≤1，則C1＝Cn.再次運用引理1可得

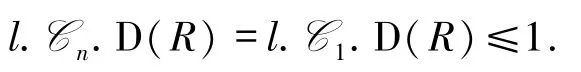
如下定理表明了左遺傳環與左Cn-遺傳環的差距.

定理9設n≥1，則對環R，以下陳述等價：

1）R是左遺傳環；

2）R是左Cn-遺傳環且w.gl.dim（R）≤1；

3）R是左C1-遺傳環且w.gl.dim（R）≤1；

4）R是左Cn-遺傳環且w.gl.dim（R）＜∞；

5）R是左Cn-遺傳環且w.gl.dim（R）≤n.

證明3）?1） 由定理4，每個1-余撓模是內射的，故R是遺傳環.

1）?2）?3）和2）?4）是顯然的，5）?1）類似于3）?1）.下證4）?5）.由上述討論，當n＝1是顯然的.現在假設n＞1.如果

則存在模M∈Fk.設B是M的第（k－n）階合沖，則fdRB≤n.由定理7，fdRB≤pdRB≤1.因此

從而n≤1，這顯然是個矛盾.從而k≤n，也就是說，w.gl.dim（R）≤n.

由文獻［26］的定理90可知，一個Noether整環R是APD當且僅當dim（R）≤1，從而有：

定理10設R是Noether整環滿足

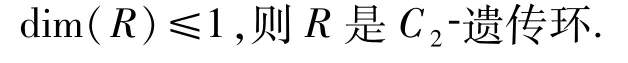
證明由文獻［27］可知

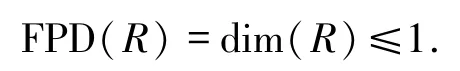
因此，由定理8，R是C2-遺傳環.

由文獻［11］的引理3.6及文獻［12］的推論6.4可知，整環R是APD當且僅當R是C1-遺傳整環.由文獻［25］的命題6和文獻［12］的推論，有如下推論.

推論4整環R是APD當且僅當

雖然整環R是C1-遺傳環當且僅當R是APD，但C1-遺傳環卻未必是幾乎完全環.

例3也可以舉出C1-遺傳環但不是幾乎完全環的例子.事實上，設D是APD但不是域，則D不是完全環，從而R＝D×D是C1-遺傳環，則I＝（D，0）≠0是R的理想.則D?R／I是R的真商環，但不是完全環.因此，R不是幾乎完全環.

致謝西華師范大學2017年度博士科研啟動專項項目（17E087）對本文給予了資助，謹致謝意.