重沸器內三甘醇-水兩相流動與沸騰換熱特性研究

李 巍，沈志恒，董 超，吳 堯，翟占虎

(1.海洋石油工程股份有限公司，天津 300452; 2.哈爾濱工業大學 能源科學與工程學院， 黑龍江 哈爾濱 150001)

0 引言

海洋氣田中心平臺在運過程需要使用三甘醇(TEG)脫水裝置對天然氣進行干燥，對于脫水裝置中重沸器內三甘醇-水的沸騰過程進行數值模擬計算，對于準確預測混合溶液中的三甘醇濃度、確定合理運行溫度區間、防止局部溫度過高等具有重要意義[1-2]。傳統對于三甘醇脫水過程的數值模擬計算大多采用ASPEN等軟件進行工藝分析，獲得不同流程上的狀態參數，該方法對于如重沸器這樣的設備的局部溫度特性的預測尚無法滿足精度要求。

李天斌[3]采用HYSYS軟件對某海洋氣田中心平臺正在運行的TEG脫水裝置進行模擬計算，對貧TEG循環量及其質量分數、再沸器溫度、汽提氣流量等參數進行模擬優化，獲得了推薦的優化參數。張明震等[4]以某油田TEG脫水裝置為基礎，利用ASPEN HYSYS建立TEG脫水裝置模擬流程，對TEG脫水裝置運行參數進行了優化對比并提出了TEG脫水裝置的最優運行參數。楊延明[5]在ASPEN PLUS軟件中將離子液體作為脫水溶劑并對其天然氣脫水過程進行模擬計算。研究發現增大TEG貧液再生溫度、循環量和吸收塔塔板數可使干氣水含量減小，同時使貧液再生熱負荷以及TEG的損失量增大，并認為離子液體是TEG的潛在替代者。Ahmad等[6]使用前饋人工神經網絡(FANN)預測TEG脫水過程中天然氣的平衡水露點，研究表明FANN可以很好地預測TEG脫水過程中天然氣的水露點。Tatar等[7]利用智能建模技術根據流體的TEG濃度和溫度預測天然氣流中的平衡水露點。林志軍[8]計算了天然氣TEG脫水時TEG對應的定性溫度、重沸器工作時對應的負荷熱及其傳熱面積，基于此設計了重沸器火管和殼體尺寸并進行校核。可以看出，目前國內外對于TEG脫水過程的數值模擬側重于采用ASPEN等軟件進行工藝上的計算，對于實際脫水過程中TEG溶液內部的流動、傳熱和蒸發過程未見詳細研究。此外，對于重沸器內部加熱管與流體的流動換熱特性也未見相關報道。

本文基于VOF方法，考慮加熱過程中流體的相變過程對溫度的影響，通過數值模擬計算獲得了重沸器中的流場和溫度場分布，并提出了一種用于評估加熱器表面溫度分布的方法。

1 計算模型

VOF方法通過兩種或多種流體(或相)沒有互相穿插這一特點，對于增加到模型里的每一附加相，就引進一個計算單元里的相的容積比率。在每個控制容積內，所有相的體積分數和為1。基于某一項的局部值，可以適當的將屬性和變量在一定范圍內分配給每一控制容積。

1.1 容積比率方程

跟蹤相之間的界面是通過求解一相或多相的容積比率的連續方程來完成的。對第q相，這個方程如下

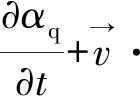
(1)

對于默認情形，上式右端的源項為零，除非給每一相指定常數或用戶定義的質量源項。容積比率方程不是為主相求解的，主相容積比率的計算基于如下的約束

(2)

1.2 動量方程

通過求解整個區域內單一的動量方程，作為結果的速度場是由各相共享的。如下所示，動量方程取決于通過密度ρ和粘度μ的所有相的容積比率

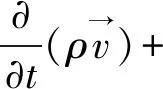
(3)

1.3 能量方程

能量方程表示如下

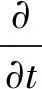
(4)

VOF模型處理能量E和溫度T是作為質量平均變量來處理的

(5)

這里對每一相的Eq是基于該相的比熱和共享溫度來確定。密度ρ和keff(有效熱傳導系數)被各項共享。源項Sh包含輻射的貢獻，也有其他容積熱源。

1.4 湍流模型

湍流模型采用RNGk-ε，該模型通過大尺度運動和修正后的粘度項體現小尺度的影響，從而將小尺度運動系統地從控制方程中去除。此外，RNGk-ε湍流模型通過在ε方程中增加一個反映主流的時均變率項，考慮了平均流動中的旋流進而修正湍流粘度。此模型表示如下

(6)

(7)

式中k——湍動能;

t——時間;

ui——時均速度;

αk，C1ε，C2ε——模型常數;

Gk——由平均速度梯度引起的湍動能k的產生項;

ε——湍動能耗散率。

1.5 界面傳熱模型

本文基于Nu數來進行流體中對流換熱系數的定義，傳熱系數hfg的值可以與Nu數相關聯

(8)

式中κf——流體的熱導率;

dg——分散相的直徑。為了確定公式(8)中的Nu數的大小，這里引入Ranz-Marshall[9-10]關系式。

(9)

式中Ref——基于分散相直徑與兩相間的滑移速度而定義的雷諾數;

Pr——主相的普朗特數。

1.6 界面傳質模型

依據Hertz-Knudsen公式，可以得到基于分子動力學的界面上的相變流量

(10)

式中p——溫度為T時可凝結氣相的分壓;

psat——溫度為T時的飽和壓力;

R——通用氣體常數。考慮到Clapeyron-Clausius方程，在飽和狀態附近壓力可以與溫度關聯起來

(11)

式中L——工質的潛熱;

vv和vl——氣相和液相的比容;

γ1——單位體積內界面蒸發調節系數，表征界面蒸發的強度大小

(12)

利用相似的思路，同樣也能得到對于冷凝的表達形式，因此界面上的傳質情況可以寫成如下的形式

(13)

2 計算模型

2.1 幾何模型

重沸器半徑為550 mm，長度約為3 700 mm，入口直徑約為400 mm，重沸器內液面高度為730 mm。重沸器加熱棒直徑16 mm，浸入長度為2 137 mm，共30根加熱棒，分為5排布置，第一排有5根，最后一排僅有1根加熱棒，其中有3根作為備用管，加熱棒中心距為24 mm，不考慮用于固定加熱棒的擋板，模型簡化后如圖1(a)所示。

圖1 重沸器幾何模型及網格劃分

考慮到重沸器內部結構復雜，且筒體徑向特征尺寸與加熱棒徑向特征尺寸相差2個數量級，需要使用較多數量的網格才能獲取足夠精度的數值結果。為了降低計算資源的消耗，本文采用多面體網格，進行網格無關性檢驗后最終確定的數量為127萬，質量在0.25以上，最終的網格如圖1(b)所示。

2.2 計算條件

對于重沸器，操作壓力為10 kPa，操作溫度為377.16 K。采用基于壓力的simple算法實施瞬態計算，過程中考察加熱棒表面溫度分布，當其分布不隨時間變化時，認為其溫度分布已經能代表真實情況下的膜溫度分布情況。

相間作用中質量傳輸選用蒸發-冷凝模型，相關參數按照冷凝器的冷凝模型計算獲得，具體參數見表1。

表1 相關物性

標準工況中，重沸器入口設置質量入口，溫度170 ℃，TEG的質量流量為0.889 kg/s，蒸汽的質量流量為0 kg/s；出口設置為壓力出口，回流溫度204 ℃；重沸器筒壁設為絕熱壁面；加熱棒壁面設為定熱流密度條件，熱流密度取20 000 W/m2。

3 計算結果及討論

3.1 時間無關性檢驗

再沸器內流體相變和流動是一個動態過程。因此計算初始的一段時間內，不合理的初始條件可能對數據造成一定的影響。因此需要進行時間無關性檢驗。

從計算的第10 s開始監測壁面溫度的分布，并將不同時刻壁面溫度在207～215 ℃范圍內的壁面占比提取出來，繪制在圖2中，可見計算開始10～11 s時，207～215 ℃的各個壁面溫度區間的概率有明顯上升，說明此時的沸騰還受到較多的初始情況的影響。而13～15 s時刻，壁面溫度的概率分布趨于一致，單調遞增的趨勢已經消失，說明此時加熱器周圍的沸騰已經進入穩定的周期過程，其溫度分布已經具有代表性。圖3是壁面最高溫度隨時間上的散點圖，其在16 s后變化不大；為保證分析的準確性,本文中后續的分析均是基于15 s之后的數值結果展開的。

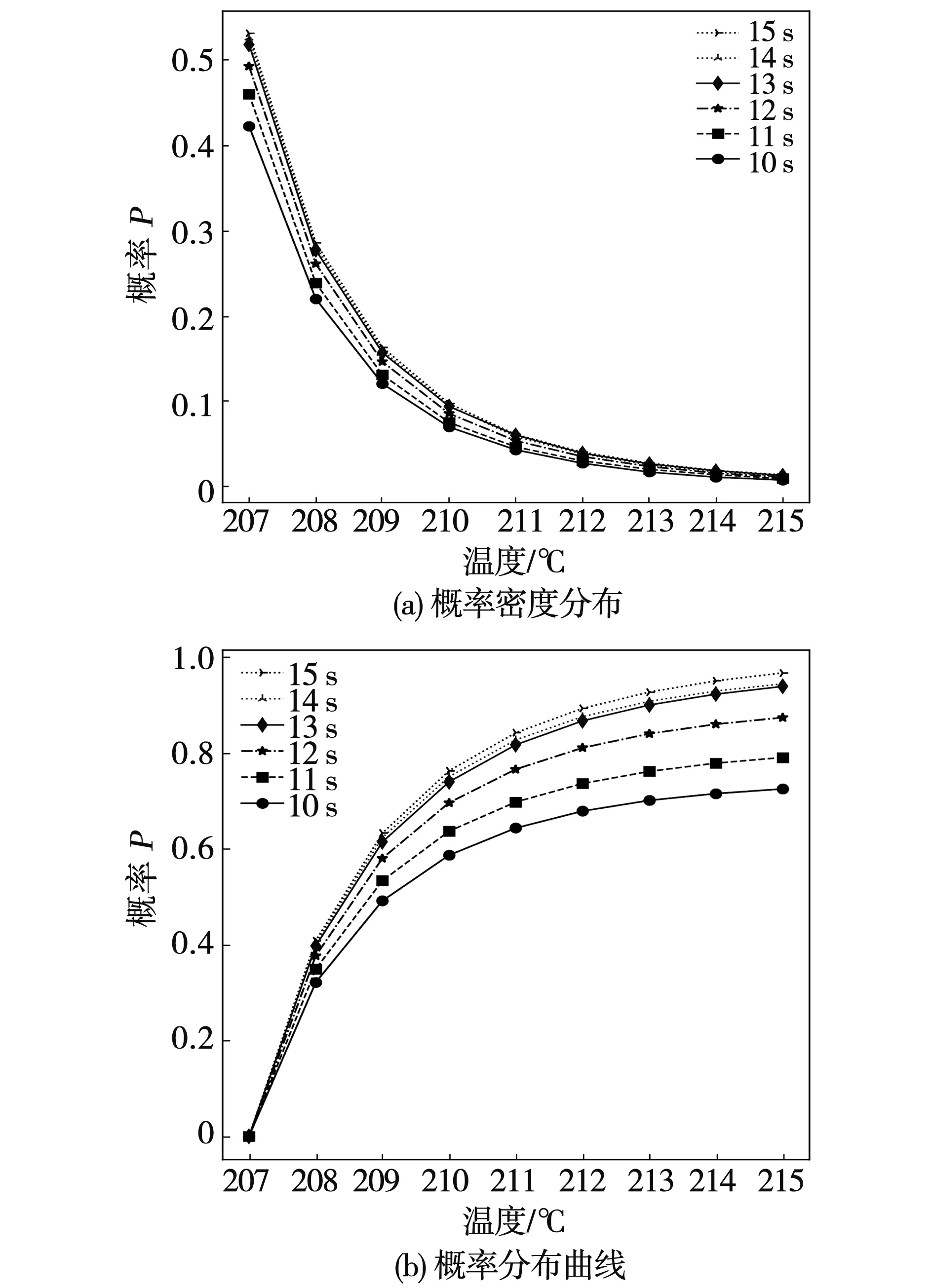
圖2 不同時刻溫度溫度分布曲線

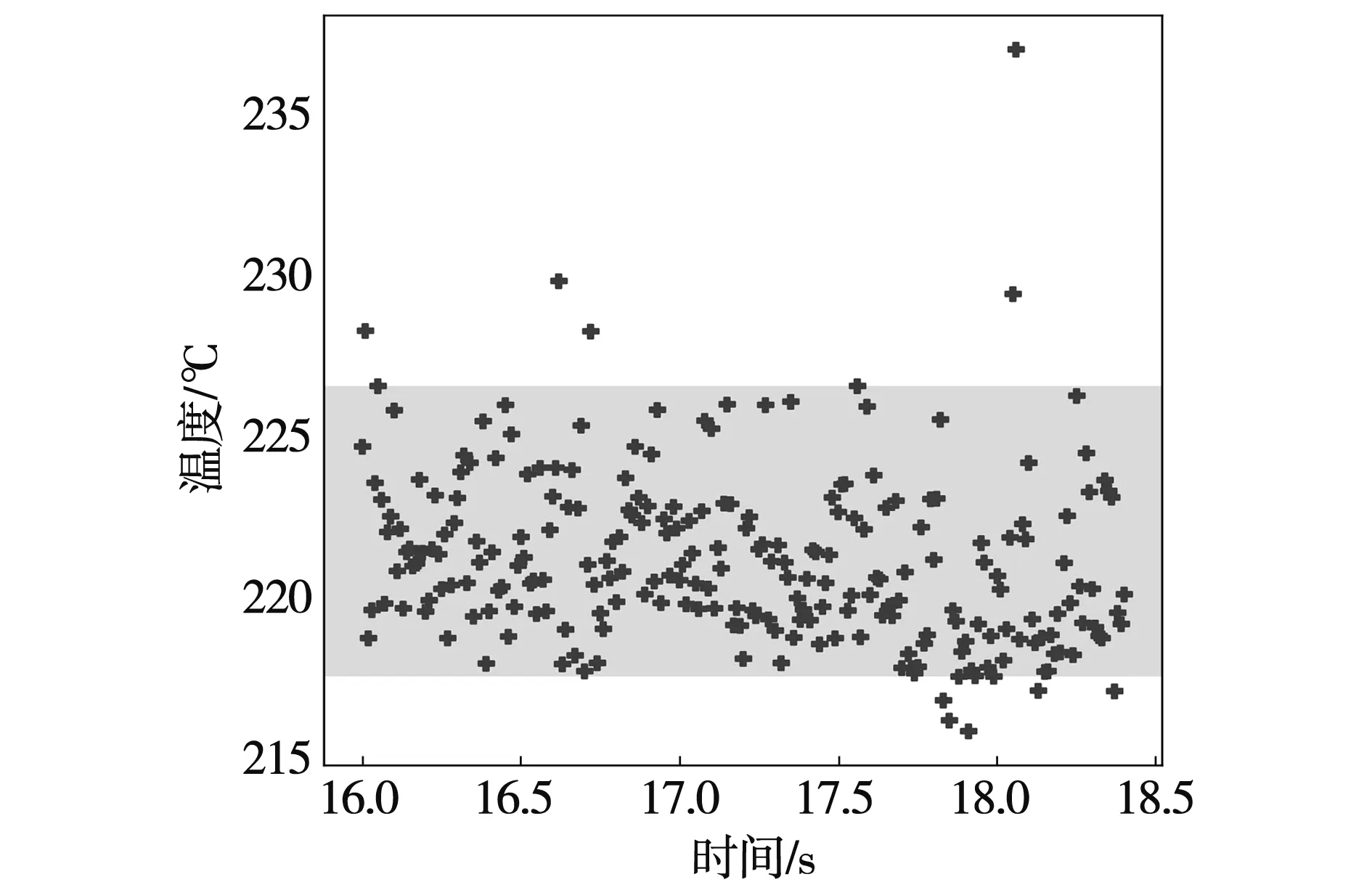
圖3 加熱棒最大溫度分布散點圖

3.1 重沸器內流場與加熱面溫度分布

圖4是加熱棒壁面溫度分布穩定后的重沸器內流體速度分布，可以看到速度最大的位置集中在加熱棒束的正上方，這是因為相變產生的氣泡在重力作用下上浮攜帶流體運動導致的。入口處呈現深藍色，這是由于循環流量變化范圍僅為2～4 m3/h，結合重沸器液相容積換算時均流速僅為1～2 m3/h，即使是入口速度也僅為0.01 m/s的數量級；遠遠小于由于氣泡上升攜帶液體和徑向熱對流引起的速度(0.3～0.5 m/s)。

圖4 重沸器內速度分布

圖5所示為重沸器內部徑向流體跡線。可以觀察到，在加熱棒束段，流動以徑向對流為主；而在重沸器遠離加熱棒束的一端，流動以沿軸向的遷移運動為主。結合圖2和圖3，管束核心區及其上部以外的區域的流體運動速度要比棒束區低1～2個數量級，即重沸器內的流動以徑向對流為主導。

圖5 重沸器內徑向不同位置流體跡線圖

圖6是監測溫度為208 ℃、212 ℃和215 ℃時的加熱器表面溫度分布，可見熱流密度為20 000 W/m2時：(1)加熱器表面能夠觀察到大量區域溫度高于208 ℃；(2)溫度高于212 ℃時的區域也可以被明顯觀察到；(3)而監測溫度提高到215 ℃時，已經基本觀察不到超溫區域。結合圖2中的溫度分布曲線，可以認為超過相應溫度的壁面面積占比低于3%時，即觀察不到明顯的超溫區域。

圖6 不同計算時刻加熱棒表面溫度分布

3.2 重沸器壁面溫度與熱流密度的關系

設置熱流密度為8 000 W/m2、12 000 W/m2、16 000 W/m2、18 000 W/m2和20 000 W/m2，其它設置均和標準算例相同，提取各個算例207～215 ℃對應的溫度分布概率，并將概率以對數坐標繪制在圖7中。可以觀察到隨著熱流密度逐漸增高，相同溫度的概率也逐漸增加；例如熱流密度從8 000增加到12 000 W/m2時，其概率分布增加了約4倍。

使用最小二乘法對圖7中的數據進行關聯，得

圖7 不同熱流密度時壁面溫度的對數概率分布

P=ekΔT+b

(14)

式中 ΔT=(Twall-T0);

Twall——壁面溫度;

T0——相變溫度/℃；

k——常數,取0.46；

b——與熱流密度q相關，可表示為

b=0.1q+3.37

(15)

其中熱流密度的單位為kW/m2。

3.3 重沸器壁面溫度與循環流量的關系

設置TEG循環流量分別為2 500 kg/h、2 800 kg/h、3 200 kg/h、3 500 kg/h和3 800 kg/h，熱流密度為16 kW/m2；提取各個算例207～215 ℃對應的溫度概率分布，并將其繪制在圖8中。

圖8 不同循環流量的溫度分布曲線

觀察圖8，可以發現從2 500 kg/h到3 800 kg/h，盡管循環流量增加了52%，而加熱管束壁面溫度概率分布幾乎沒有變化(相比于熱流密度從12 kW/m2變化到20 kW/m2)。

結合再沸器內流場分析結論，認為這是圖8中的現實是因為再沸器容積較大，內部流動主要時相變產生的氣泡攜帶流體產生的徑向對流，而增加循環流量對重沸器內部流場影響十分有限；所以可以認為常規范圍內，重沸器內加熱器壁面溫度不受循環流量的影響。

4 結論

本文采用VOF方法結合相變傳熱模型對重沸器內兩相流動及傳熱過程進行了數值模擬計算，對8 000 ～ 20 000 W/m2范圍內熱流密度和TEG循環流量下的重沸器內部流場和溫度場進行了數值模擬，主要結論如下：

(1)相變溫度固定為208 ℃時，加熱器表面的在207～215 ℃區間的概率密度分布程倒指數分布規律，其分布受加熱器熱流密度影響顯著，，相關計算式可以用表示如下

P=ekΔT+b

(2)重沸器內流場以氣泡上浮產生的徑向熱對流為主，加熱管束上方區域的流體速度高出由于循環流量引起的軸向遷移速度1～2個數量級，因此TEG循環流量對加熱器壁面溫度的影響可以忽略不計。

(3)同時研究發現由于氣泡沿壁面向上的遷移運動，加熱器上表面高溫概率高于下表面；因此，重沸器的設計過程中應當注意通過合理布置加熱管等方式加以解決。