鋼橋面板-肋雙面焊構造細節疲勞失效模式研究

吳 波

（中國市政工程西南設計研究總院有限公司，四川 成都610081）

0 引言

正交異性鋼橋面板由三個不同方向的板件通過焊接連接而形成，具有自重輕、承載能力突出等優勢。作為21世紀大跨度橋梁中廣泛應用的橋面板形式，其靜力特性、制造工藝和疲勞損傷等方面也被越來越多的學者進行研究，其中疲勞損傷問題是鋼橋面板最為關鍵的問題。近年來，由于車流量增大，重車比例增多的趨勢更加顯著，鋼橋面板眾多構造細節往往在尚未到達設計使用年限前出現一系列疲勞裂紋，對于鋼橋面板-肋焊接細節而言，隨著疲勞損傷逐漸累積，裂紋將裂穿頂板導致U肋銹蝕，威脅結構行車安全[1-2]。

近年來，國內橋梁建設中陸續采用U肋內焊技術，形成鋼橋面板-肋雙面焊構造細節以期提高疲勞抗力，羅鵬軍等[3]和張清華等[4]分別從切口應力法和模型試驗法角度證明了板-肋雙面焊構造能夠改善傳統單面焊的疲勞抗力。然而，獲取鋼橋面板典型構造細節疲勞失效模式力學特征是認識該細節疲勞性能的基礎，目前關于鋼橋面板-肋雙面焊構造細節的相關研究依然有待更為系統的提升與完善。斷裂力學分析方法作為一種最為直接有效的手段是探究該細節疲勞特性的重要工具，本文基于線彈性斷裂力學原理，在鋼橋面板-肋雙面焊構造細節裂紋萌生點處引入初始裂紋，采用ABAQUS有限元軟件建立包含裂紋體的有限元模型，通過分析裂紋潛在的擴展能力，從而確定該細節各疲勞失效模式的疲勞性能，在此基礎上確定主導疲勞失效模式。

1 研究對象

鋼橋面板板-肋構造細節根據所處位置分為橫隔板節間內（RD細節）和橫隔板位置處（RDF細節）兩類[5]。目前研究中，橫隔板節間內疲勞裂紋是主要研究熱點，且其實橋中疲勞開裂占比較大。此處主要以橫隔板節間內的板-肋雙面焊構造細節為研究對象，其中全熔透雙面焊技術由于焊接工藝難以保證，分析時以工程中常見的外側75%熔透的部分熔透焊為研究對象，該細節共包含8種疲勞失效模式，鋼橋面板構造細節分類與雙面焊疲勞失效模式見圖1。

圖1 鋼橋面板構造細節分類與雙面焊疲勞失效模式

2 節段模型選取和有限元模型建立

2.1 疲勞節段模型尺寸

以某斜拉橋工程鋼橋面板為分析對象，為反映模型實橋受力狀態，參考相關研究文獻[3]，縱向選取三跨，即4個橫隔板間距（橫隔板間距為2.5 m）、橫向選取5個U肋作為疲勞節段模型進行分析，主要板件厚度為：頂板厚18 mm，橫隔板厚14 mm，U肋尺寸300 mm×300 mm×8 mm（上開口寬×高×板厚）,U肋橫向間距為600 mm，考慮到對稱性，關注位置取第2跨跨中中間U肋與頂板相交處，所選取的疲勞節段模型與板-肋雙面焊構造細節尺寸見圖2，圖2中參數α和β分別為50°和130°。

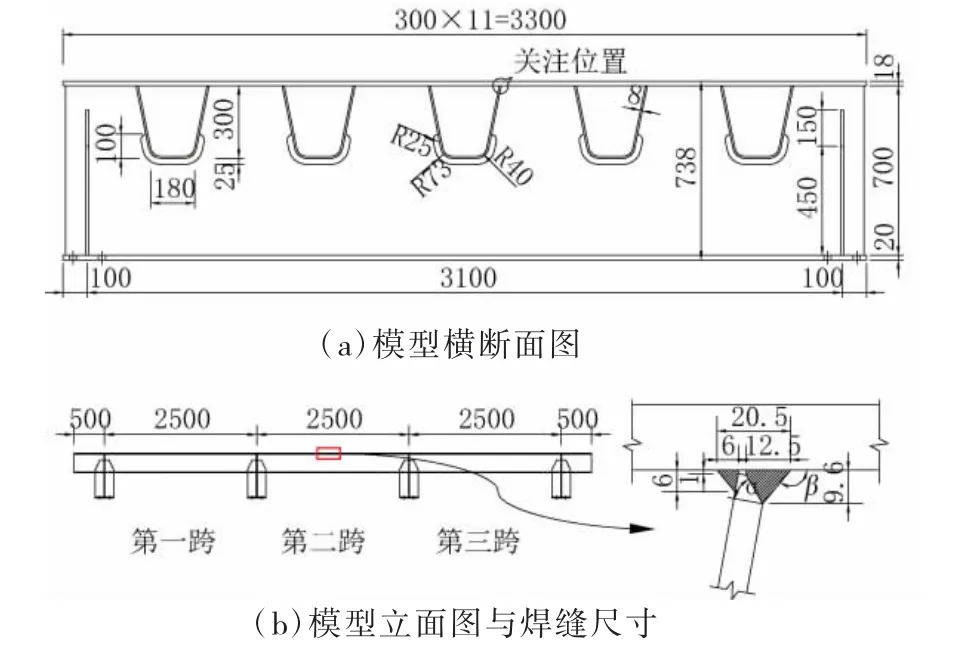
圖2 疲勞節段模型和板-肋雙面焊相關尺寸（單位：mm）

2.2 初始焊接缺陷和加載工況

相關研究文獻表明面狀缺陷相比于體缺陷更為不利，為真實反映焊接工藝所引起的初始焊接缺陷的影響，參考文獻[6]，選取初始裂紋形式為半圓形裂紋，初始裂紋深度a0與1/2裂紋長度c0均為0.5 mm，節段模型疲勞車輪荷載采用歐規（Eurocode 3）標準疲勞車輛荷載模型Ⅲ形式（單車模型）[7]，單輪輪載面積為400 mm×400 mm，軸重為120 kN，考慮3倍超載影響，選取的受力較為不利加載位置為單側前后輪對稱作用于第二跨板-肋雙面焊構造細節跨中關注位置處。

2.3 有限元模型

采用ABAQUS有限元軟件建立了適合本文疲勞失效模式分析的有限元模型，見圖3。

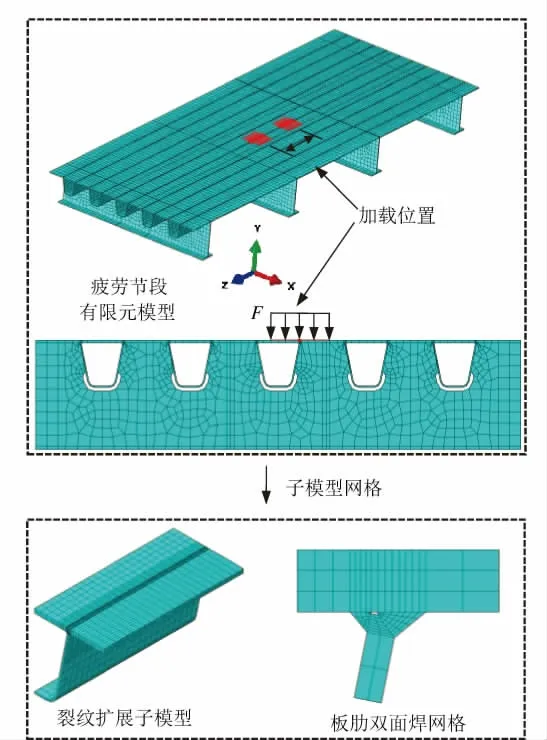
圖3 有限元模型

建模過程如下：先建立三跨5U肋疲勞節段有限元模型，模型橫隔板底部區域200 mm×300 mm（橫向×縱向）進行X向、Y向和Z向位移約束，以模擬實際橫隔板遠離約束部分處于彈性支承狀態。然后跨中加載區域中間位置橫向取150 mm，縱向取400 mm，豎向取U肋高度作為裂紋擴展有限元子模型，并對板-肋雙面焊構造細節焊縫區域進行網格細化，焊縫區域網格尺寸控制在3 mm內，以確保分析結果的準確性。疲勞節段有限元模型實體單元為C3D8R，裂紋擴展子模型實體單位為C3D20R，偏安全考慮，不計鋪裝層對輪載的擴散作用。

3 各疲勞失效模式結果分析

3.1 應力強度因子

應力強度因子反映了裂紋的擴展能力，其數值越大，裂紋擴展越快。基于線彈性斷裂力學原理，采用相互作用積分方法裂尖Ⅰ型（張開型）、Ⅱ型（滑開型）和Ⅲ型（撕開型）應力強度因子，參考文獻[6]，等效應力強度因子幅值ΔKeff可由I型應力強度因子幅值ΔKⅠ、Ⅱ型應力強度因子幅值ΔKⅡ和Ⅲ型應力強度因子幅值ΔKⅢ通過式（1）計算得到。

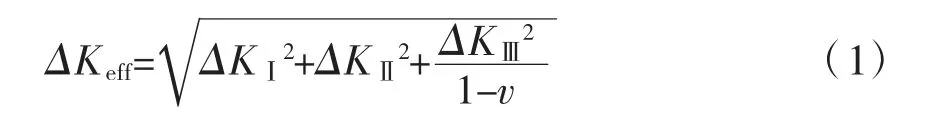
當等效應力強度因子幅值達到擴展閾值ΔKth（ΔKth=63 N·mm-3/2）時裂紋開始擴展，其數值越大擴展能力越強。

3.2 疲勞失效模式分析

相關文獻研究表明焊縫熔透率達到75%可避免沿焊縫擴展的疲勞裂紋[1]，即圖1中的模式Ⅴ和模式Ⅷ，本次疲勞失效模式分析主要針對沿頂板開裂的模式Ⅰ到模式Ⅳ，及沿U肋開裂的模式Ⅵ和模式Ⅶ。

將初始焊接缺陷引入到各疲勞失效模式裂紋萌生點處，以模式Ⅰ為例，裂紋位置示意見圖4。

圖4 模式Ⅰ裂紋位置示意圖

通過有限元數值計算，提取各失效模式裂紋前緣點等效應力強度因子幅值，將裂尖前緣路徑按照從0到1進行劃分，計算結果見圖5。

圖5 等效應力強度因子幅值變化曲線

由圖5得到：（1）失效模式Ⅰ和失效模式Ⅳ等效應力強度因子幅值達到擴展閾值，裂紋具有擴展能力；（2）板-肋雙面焊構造細節焊根部位在本文所選取的初始焊接缺陷下不會引起構造細節疲勞開裂，該部位不是焊接質量控制的重點；（3）沿U肋厚度方向開裂的疲勞失效模式能夠承受實橋3倍的超載影響，其擴展能力低于沿頂板厚度方向開裂的疲勞失效模式。

當疲勞荷載較大時，由本文計算結果來看，沿頂板開裂的失效模式I更容易產生疲勞裂紋，國內研究者通過對深中通道鋼橋面板雙面焊構造細節足尺模型試驗，獲得了該失效模式的疲勞裂紋[8]，見圖6。

圖6 文獻[8]圖片

由于沿頂板厚度方向開裂的疲勞失效模式Ⅰ和失效模式Ⅳ初始裂紋前緣等效應力強度因子幅值數值較為接近，并且均具有擴展能力，此處以裂紋擴展至板厚1/2（即9 mm）為疲勞失效判據，裂紋擴展步長控制在0.4 mm左右，得到兩種疲勞失效模式的等效應力強度因子幅值隨裂紋深度方向的變化曲線見圖7。

圖7 模式Ⅰ和模式Ⅳ等效應力強度因子幅值對比

計算結果表明：（1）疲勞失效模式Ⅰ和失效模式Ⅳ在達到9 mm前，二者擴展速率始終不斷增大，隨裂紋深度增加，擴展速率的變化率逐漸減小，在達到9 mm時兩者擴展速率有達到最大值的趨勢；（2）在本文加載工況下，模式Ⅰ為板-肋雙面焊構造細節主導疲勞失效模式，其擴展速率始終大于模式Ⅳ；（3）兩種疲勞失效模式在擴展過程中，由于等效應力強度因子幅值較大于其擴展閾值，表明裂紋整體均具有較強的擴展能力，在焊接過程中應避免頂板焊趾處引入夾雜等缺陷，從源頭控制裂紋的發生。

4 結論

本文基于線彈性斷裂力學基本理論，采用ABAQUS有限元軟件，建立了包含裂紋體的鋼橋面板-肋雙面焊構造細節的數值有限元分析模型，在本文節段模型尺寸條件下主要得到以下結論：

（1）采用ABAQUS有限元軟件，實現了疲勞裂紋擴展數值模擬。

（2）分析了板-肋雙面焊構造細節各疲勞失效模式等效應力強度因子幅值水平，闡明了較為容易發生疲勞裂紋的失效模式。

（3）在本文加載工況下，確定了疲勞失效模式Ⅰ為板-肋雙面焊構造細節的主導疲勞失效模式。