基于自適應MPC的自動駕駛汽車軌跡跟蹤控制

范賢波， 彭育輝， 鐘聰

(福州大學機械工程及自動化學院， 福建 福州 350108)

0 引言

近年來， 智能交通、 人工智能技術快速發展， 自動駕駛已成為各領域的研究熱點. 作為支撐汽車自動駕駛的關鍵技術之一， 軌跡跟蹤要求控制車輛使之能夠按照參考軌跡行駛， 如何確保跟蹤的精確性和穩定性一直是無人駕駛控制技術重點與難點[1]. 因此， 在不同工況下， 確保自動駕駛汽車的跟蹤精度和穩定性顯得尤為重要.

目前應用在軌跡跟蹤橫向控制算法主要有： 滑模控制[2]、 PID控制[3]、 線性二次調節器控制[4]、 模型預測控制[5]等. 由于模型預測控制(model predictive control, MPC)能夠系統地處理車輛系統中存在的動力學和運動學約束， 被廣泛應用于自動駕駛汽車軌跡跟蹤橫向控制中. 為提高自動駕駛汽車軌跡跟蹤精度和穩定性， 文獻[6-7]中設計一種MPC自適應控制器， 基于線性輪胎模型在線實時估計輪胎側偏剛度并更新控制器預測模型， 但未考慮中高速工況下輪胎的非線性特性； 文獻[8-9]在MPC控制器中加入車輛行駛狀態參數估計器， 仿真結果表明， 帶參數估計器的MPC控制器能夠較好地實現智能車輛在恒定車速下的軌跡跟蹤， 但由于采用了固定控制參數， 在車速變化時控制效果并不理想； 文獻[10]利用遺傳算法(GA)對MPC的預測時域、 控制時域這兩個重要參數進行優化， 經過GA優化的MPC控制器提高了對速度變化的自適應能力. 文獻[11]基于模型預測控制算法設計一種可變預測時域的軌跡跟蹤控制器， 提高了控制器對速度的自適應性.

綜合目前的研究成果， 無人駕駛汽車的模型預測控制器較少考慮預測模型參數失配、 橫向車速和縱向車速對軌跡跟蹤精度與穩定性的影響. 為此， 本文提出一種自適應軌跡跟蹤控制方法， 通過改進模型參數估計方法， 提高輪胎側偏剛度參數估計的精度， 避免模型參數失配而引起的車輛失穩問題； 并設計控制參數選擇器， 根據橫向車速與縱向車速自適應選取預測時域， 提高軌跡跟蹤控制器的自適應性.

1 車輛動力學模型及參數估計

1.1 車輛動力學模型

以三自由度車輛動力學模型作為軌跡跟蹤的研究對象， 包括： 縱向x、 橫向y和橫擺Iz3個自由度.如圖1所示， 坐標系{o-xyz}為固定在車輛質心處的滿足右手定測的車輛坐標系， 坐標系[O-XY]為地面的全局坐標系[12].

圖1 車輛動力學模型Fig.1 Vehicle dynamics model

根據牛頓第二定律， 分別可得到縱向 、 橫向、 橫擺3個自由度方向的受力平衡方程， 如下所示：

(1)

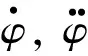
Fl=Cls;Fc=Ccα

(2)

式中：Cl,Cc分別為輪胎縱向和側向剛度；s,α分別為輪胎滑移率與側偏角.

聯合式(1)～(2)并考慮車輛坐標系與慣性坐標系之間的變換關系簡化推導后， 得到車輛動力學非線性模型狀態方程如下：

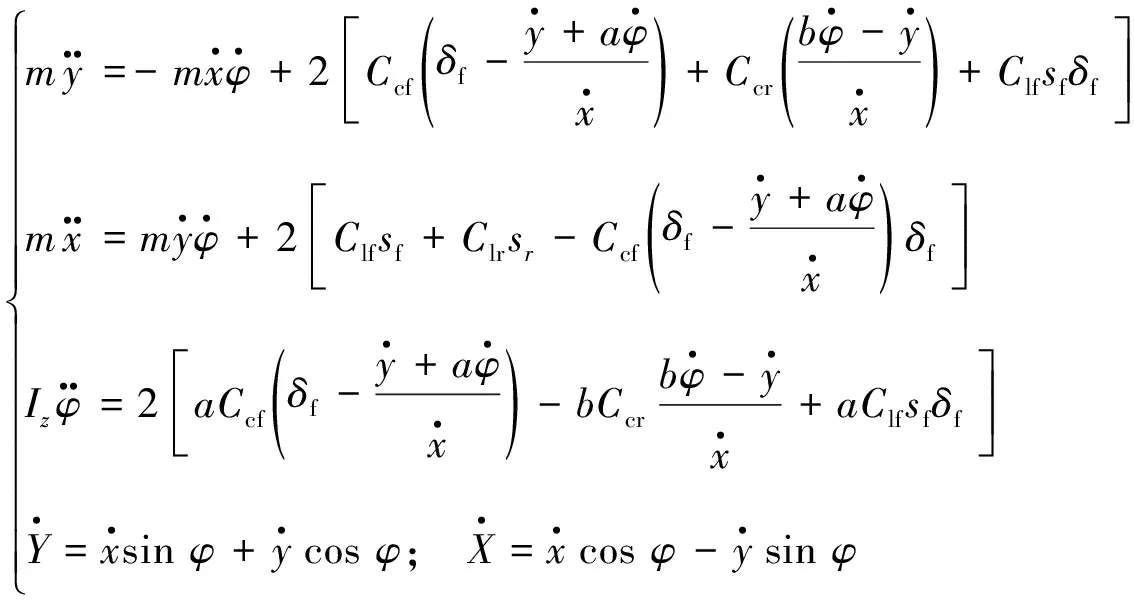
(3)

式中：Clf,Clr，Ccf,Ccr分別為前、 后輪胎縱向剛度和側向剛度.

1.2 輪胎側偏剛度估計

如圖2所示， 側偏角在較小范圍內(-5° ～5°)時， 輪胎側偏力與側偏角成線性關系， 即:

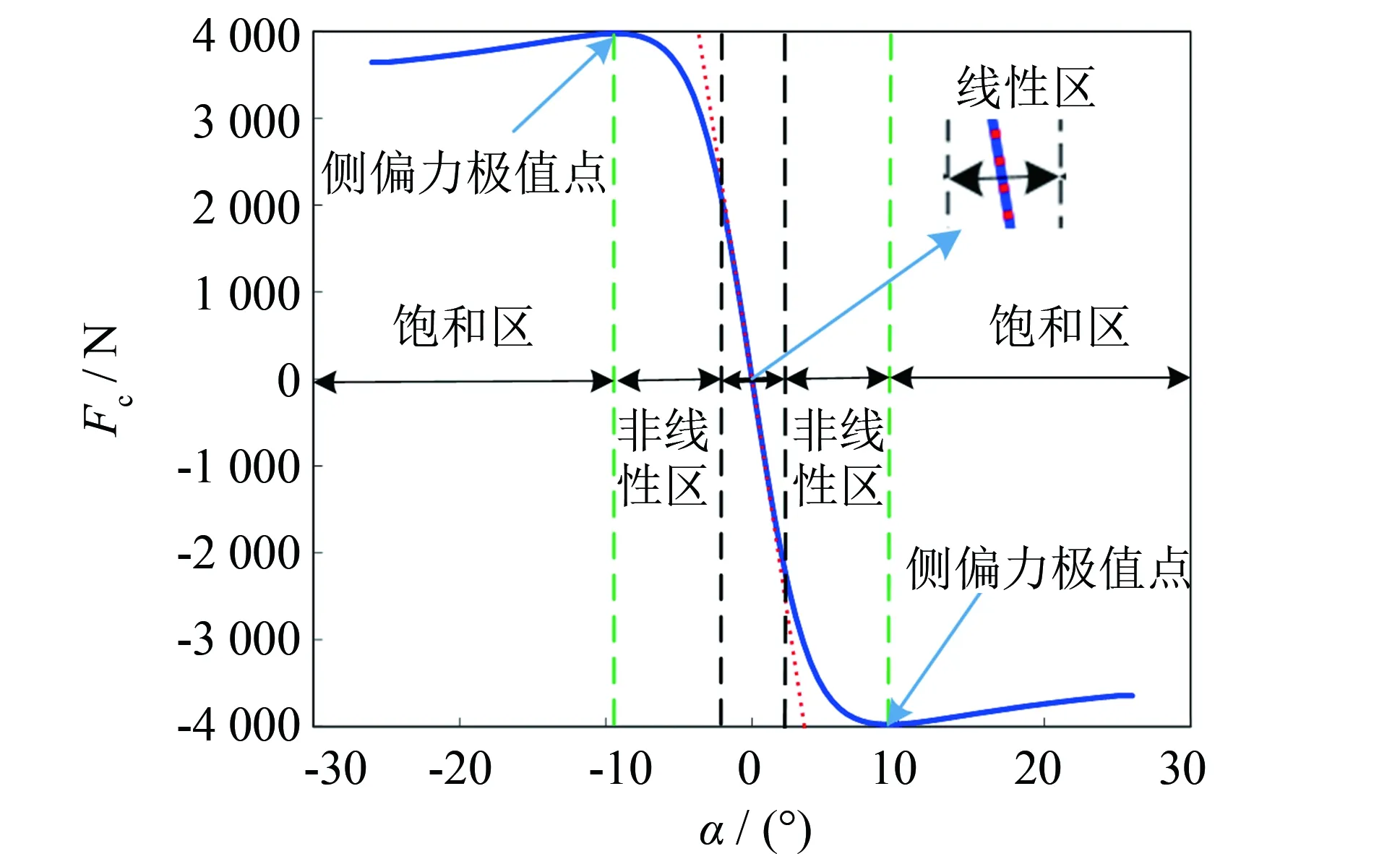
圖2 側偏特性曲線Fig.2 Side slip characteristic curve

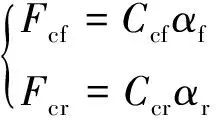
(4)

αf,αr分別表示前后輪側偏角，Ccf,Ccr分別表示前后輪側偏剛度. 當車輛在中高速工況下曲線行駛時， 隨著輪胎側偏角逐漸增大， 輪胎進入非線性區， 側偏力逐漸接近附著極限， 達到側偏力極值點后進入飽和區， 為防止輪胎進入飽和區， 在模型預測控制器中增加了側偏角約束.

根據Fiala輪胎側偏特性公式[13]， 建立輪胎側偏角與側向力的非線性模型, 采用卡爾曼濾波算法進行估計附著系數[14]. 為便于側偏剛度估計， 將非線性模型轉化為遞推最小二乘算法的標準形式.

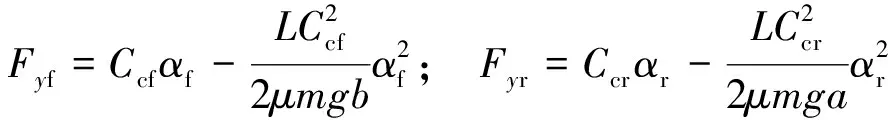
(5)

Z(k)=hT(k)θ+e(k)

(6)

圖3為不同車速下的輪胎側偏角曲線， 當車速較高且曲線行駛時， 輪胎進入非線性區. 圖4為50 km·h-1下的側偏剛度估計結果， 可見采用非線性模型的參數估計精度略高于線性模型， 但無明顯差異. 圖5為車速75 km·h-1下的側偏剛度估計結果， 可見改進的模型參數估計方法估計精度明顯高于采用線性模型的估計精度， 利用平均絕對百分比誤差進行評價， 該車速下估計精度提高了32.52%. 這是因為車輛在中高速下曲線行駛， 輪胎進入非線性區域， 采用線性模型會因為模型不匹配導致參數估計精度的降低， 車輛高速行駛時對控制器模型精度要求更高， 所以提高模型參數的估計精度是很有必要的.

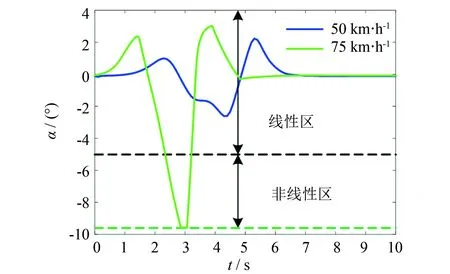
圖3 不同車速下的輪胎側偏角Fig.3 Tire slip angle under different vehicle speed

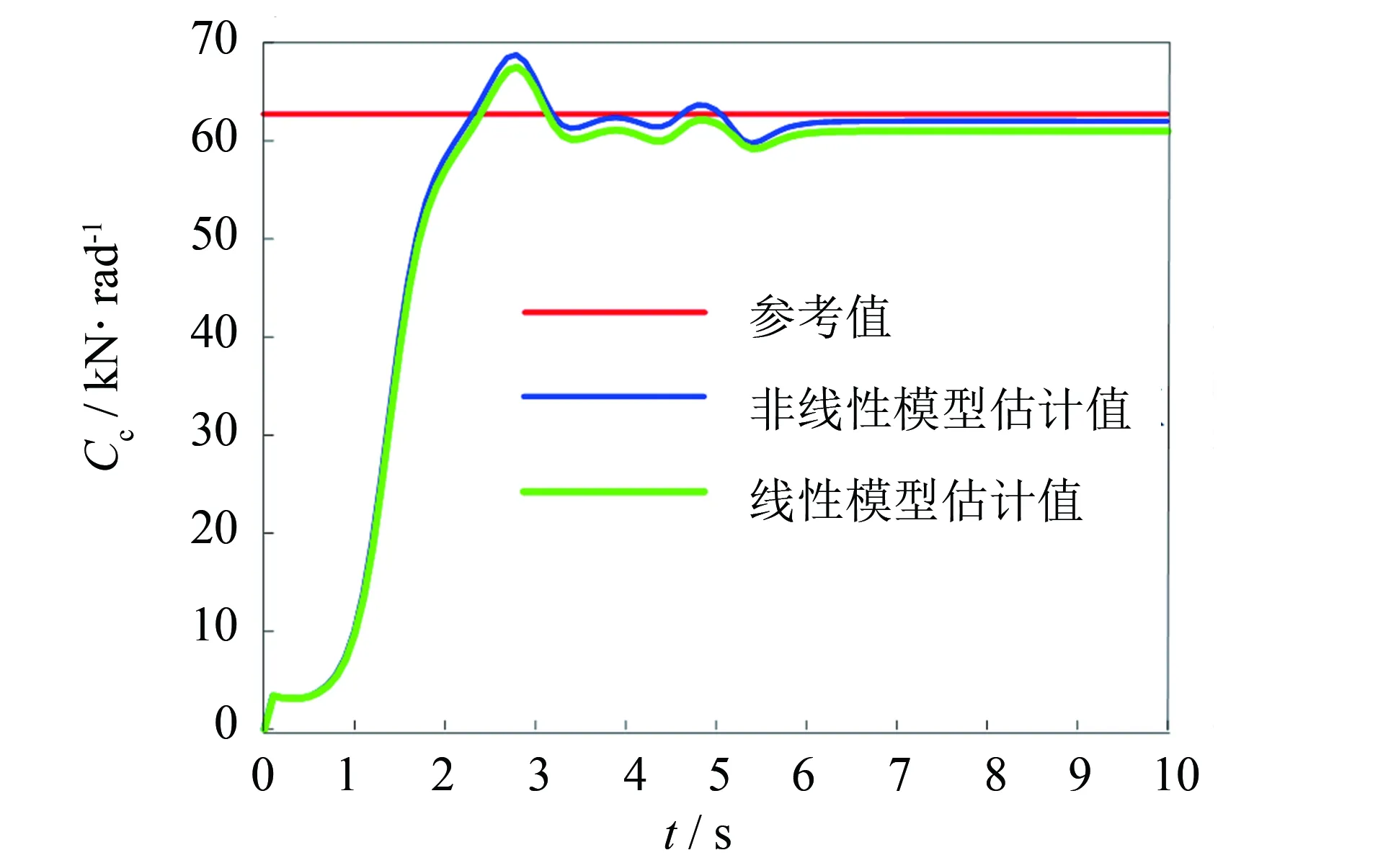
圖4 50 km·h-1下側偏剛度估計結果Fig.4 Estimation results of cornering stiffness at 50 km·h-1

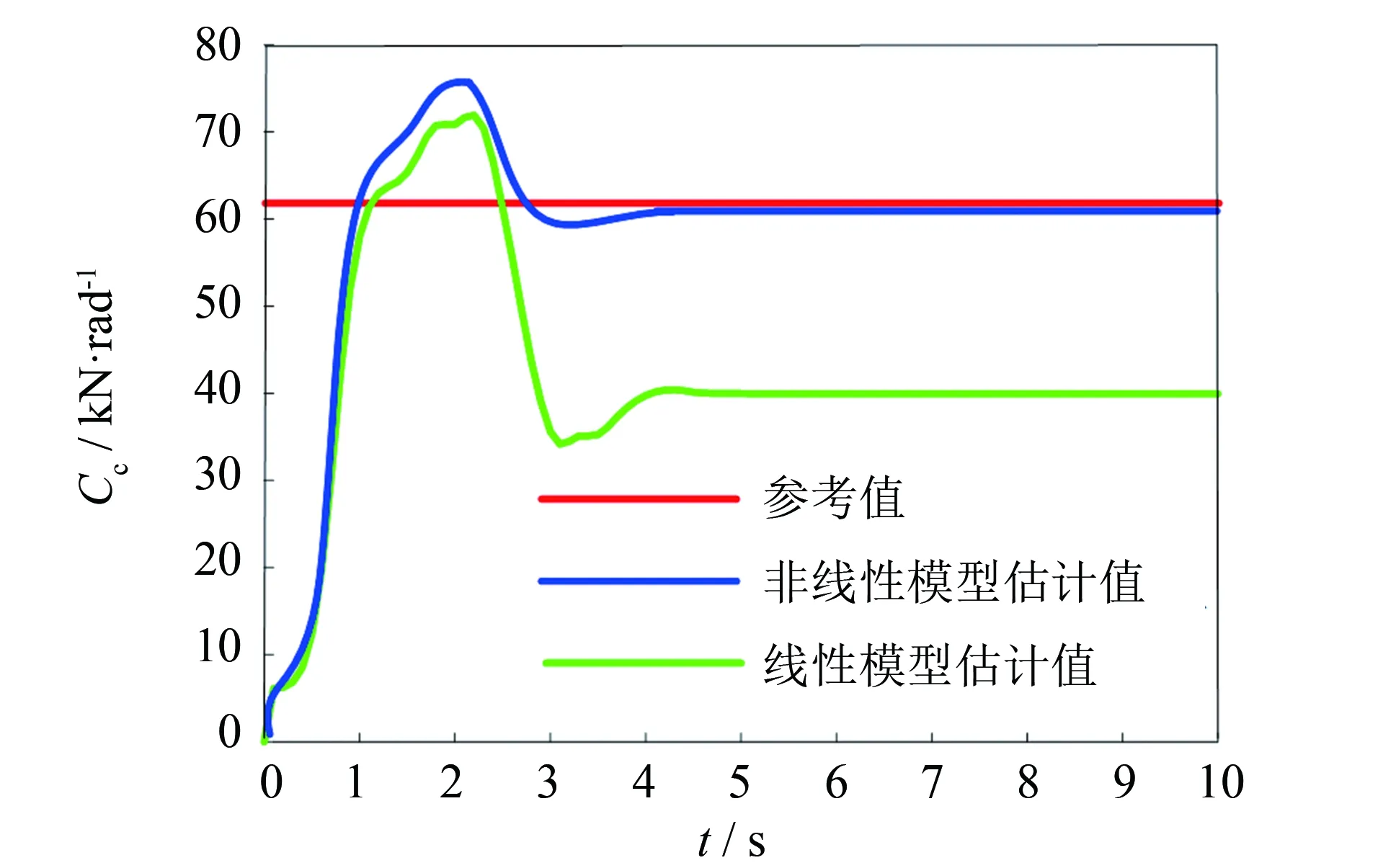
圖5 75 km·h-1下側偏剛度估計結果Fig.5 Estimation results of cornering stiffness at 75 km·h-1

2 自適應模型預測控制器設計

本研究設計的自適應控制器結構如圖6所示， 分為MPC控制器、 控制參數選擇和參數估計器三個部分. 參考軌跡信息是已知的， 為了提高控制器的自適應能力， 根據實時橫向車速和縱向車速， 基于設計的模糊控制規則自適應地選擇預測時域與控制時域. 同時， 為了提高車輛行駛的穩定性， 進行在線估計輪胎側偏剛度， 并將估計的參數值實時更新控制器預測模型， 提高控制器預測模型對系統狀態量和輸出量的預測能力， 保證車輛行駛穩定性.

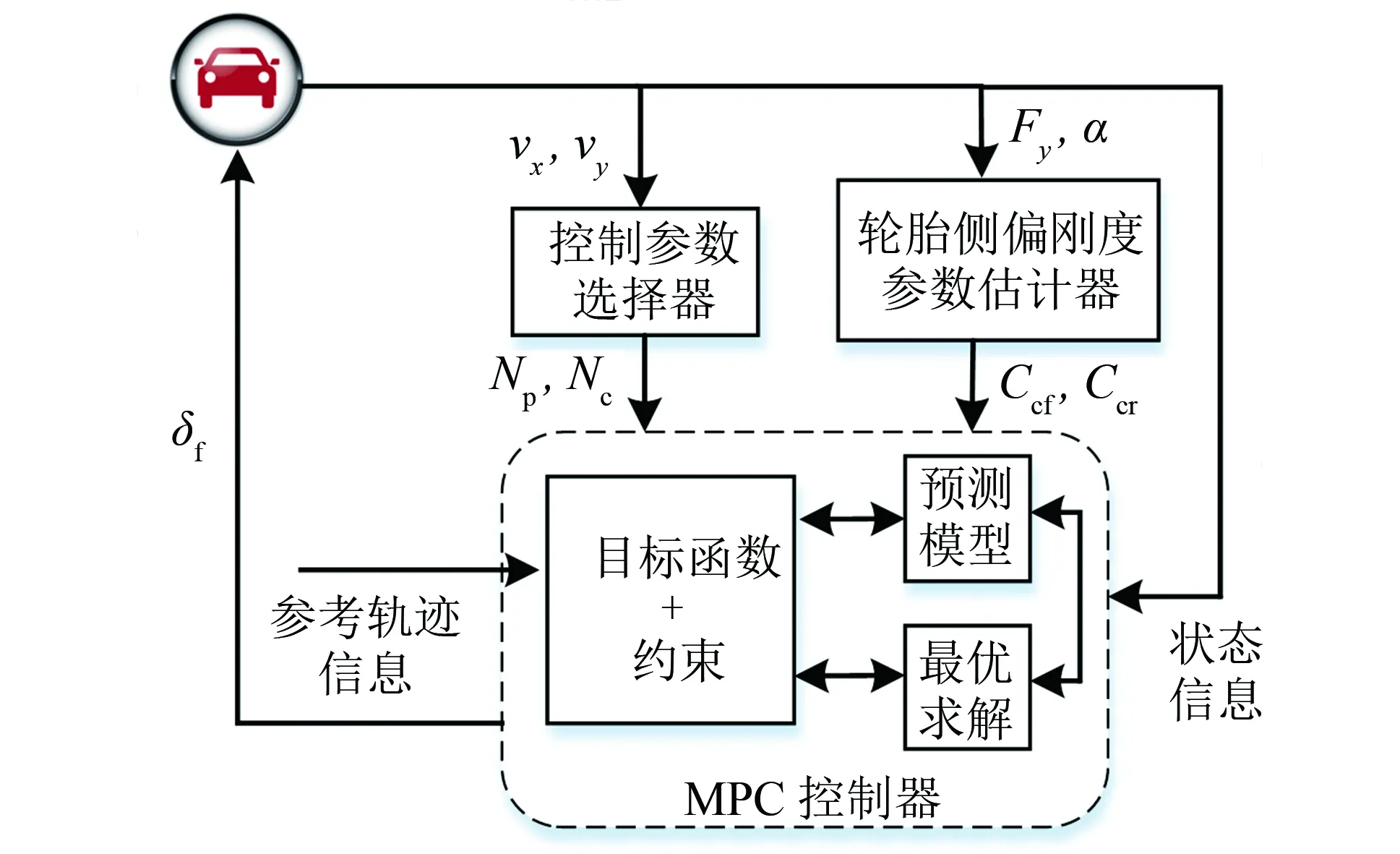
圖6 自適應控制器框架圖Fig.6 Frame diagram of adaptive controller

2.1 預測模型

公式(3)建立的車輛動力學模型的連續狀態方程可表示為：

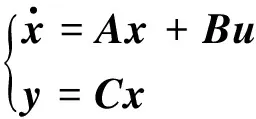
(7)

由于該控制系統屬于非線性時變系統， 對于控制器求解比較困難， 采用前進歐拉法對系統進行線性處理， 時間步為k， 則式(7)可以被描述為：

(8)

式中：Ak=I+TsA；Bk=TsB；Ts為系統采樣時間.

為了更好地約束控制增量， 設

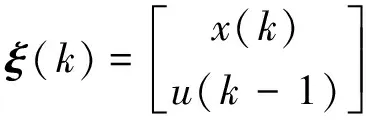
(9)

得到預測模型遞推公式如下：

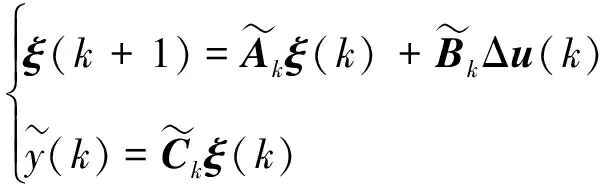
(10)

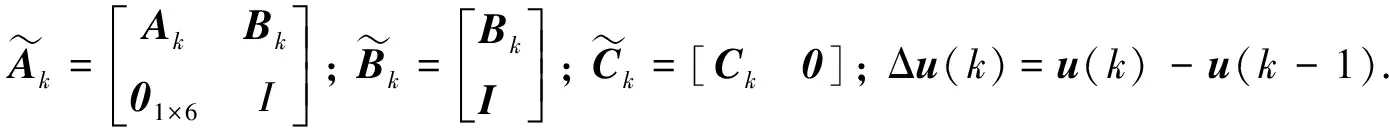
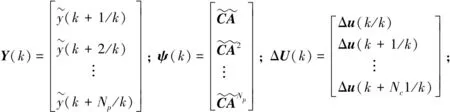
設系統預測時域為Np， 控制時域為Nc， 系統在預測時域內的輸出量可以表示為：

Y(k)=ψ(k)ξ(k)+Θ(k)ΔU(k)

(11)

2.2 目標函數與優化求解

參考橫向位置Yref和參考橫擺角φref是已知量， 作為參考輸出信號輸入系統， 用來計算車輛的實時橫向位置偏差和橫擺角度偏差. 控制的最終目標就是要讓被控車輛盡可能地按照參考軌跡行駛， 使得橫向位置偏差和橫擺角度偏差接近于0， 同時為了保證行駛穩定性還要使控制量變化率盡量小， 因此目標函數可以構建為如下形式：

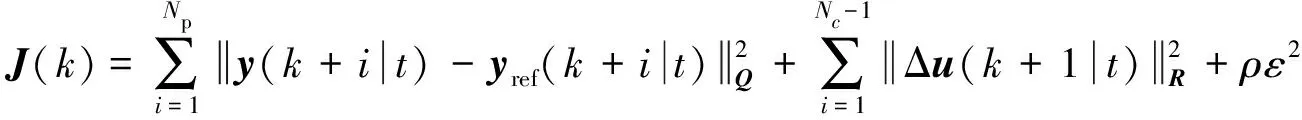
(12)

式中：Np為預測時域；Nc為控制時域；Q和R為權重矩陣；yref表示參考輸出；ρ為權重系數；ε為松弛因子. 第一項表示輸出量與參考輸出量之間的誤差， 反映了控制目標的精確跟蹤； 第二項為控制增量的大小， 主要反映控制目標的穩定性. 設置松弛因子， 是為了保證二次規劃具有最優解. 同時， 考慮實際車輛的運動學與動力學特性， 還需要對系統的狀態量和控制量進行一定的約束， 包括： 1) 輸出量約束：ymin≤y(k)≤ymax； 2) 側偏角約束：αmin≤α≤αmax； 3) 控制量約束：umin≤u(k)≤umax； 4) 控制增量約束： Δumin≤Δu(k)≤Δumax.

將目標函數(12)轉化成便于計算機求解的帶約束的標準二次規劃形式：

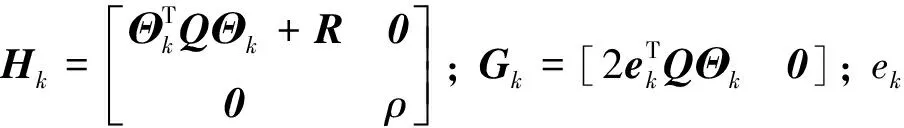
在每一個優化周期內， 優化目標為minJ， 得到控制時域內的控制變量的增量：

ΔU=[Δu*(k), Δu*(k+1), …, Δu*(k+Nc-1)]

(14)

選取控制序列的第一個元素作為實際的控制變量輸出， 即前輪轉角， 作用于被控對象：

u(k)=u(k-1)+Δu*(k)

(15)

2.3 預測時域和控制時域選擇

預測時域和控制時域的選取對軌跡跟蹤的精度和穩定性有很大的影響， 預測時域和控制時域的大小可以理解為預測距離的長短， 該距離的長短會受到縱向車速與采樣時間的影響.

d=vx×Np×Ts

(16)

當預測時域和采樣時間不變時， 預測距離會隨著縱向車速增大而增大， 如果預測距離過大， 控制器將會增大距離較遠處的誤差權重， 導致當前車輛附近的軌跡跟蹤精度下降； 如果預測距離過小， 將可能致使控制量以及控制增量超出約束值， 導致車輛無法及時轉向， 降低車輛的穩定性. 同樣， 控制時域過大， 將會增加控制器的計算負擔， 而控制時域過小， 使得控制器對誤差過于敏感， 使得車輛的穩定性下降. 因此， 預測時域和控制時域的選取應該考慮實時縱向車速和橫向車速的大小， 基于此， 引入一種控制參數因子， 預測時域和控制時域可以被描述成縱向車速、 橫向車速和控制參數因子的一種函數關系：

Np=f(vx,vy,κ)

(17)

式中：κ為控制參數因子.

采用模糊控制， 根據縱向車速和橫向車速對控制參數因子進行調節， 采用高斯型和三角形隸屬度函數， 制定了如表1所示的模糊規則， 模糊規則縱向車速和橫向車速這兩個輸入與輸出控制參數因子的響應關系如圖7所示.

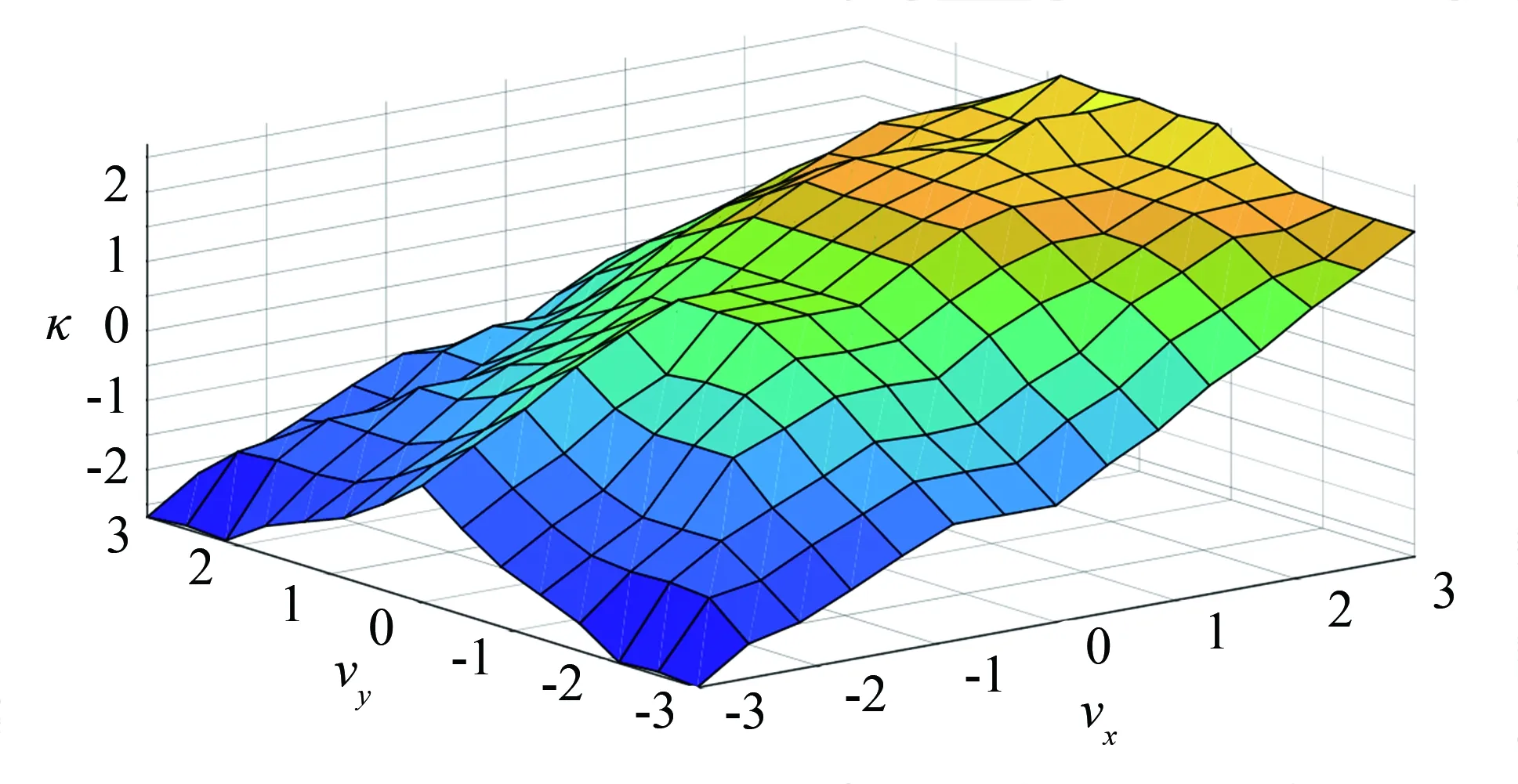
圖7 控制參數因子與車速關系圖Fig.7 Relationship between control parameters factor and vehicle speed

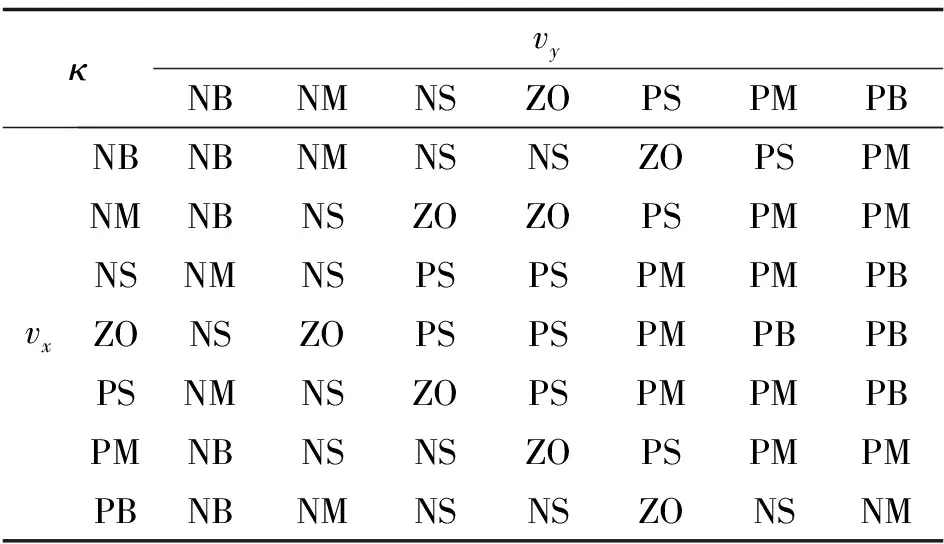
表1 模糊控制規則

為進一步提升控制參數因子的自適應能力， 需要充分考慮縱向車速和橫向車速對預測時域和控制時域的影響. 當車輛在直線道路上行駛時， 橫向車速很小， 此時預測時域和控制時域可以相應長一些； 當行駛軌跡曲率較大時， 橫向車速會隨著道路曲率的增加而增加， 而在軌跡曲率較大的情況下， 為了確保行駛穩定性， 預測時域和控制時域要相應減小， 而控制時域又不能太小； 因此預測時域和控制時域可通過以下公式計算得到：

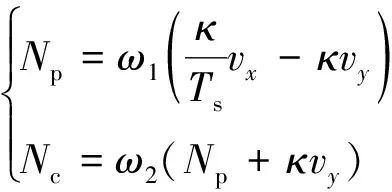
(18)

式中：κ為控制參數因子；Ts為采樣時間， 取0.1 s；ω1,ω2為時域權重系數.

3 仿真分析

為驗證所提出的自適應模型預測控制器的有效性， 基于Simulink/CarSim軟件構建聯合仿真模型對所提控制方法進行計算機仿真分析. 仿真分析實驗1: 進行雙移線工況仿真實驗， 分析確定預測時域權重系數和控制時域權重系數； 仿真分析實驗2: 超車軌跡跟蹤仿真， 驗證加入參數實時估計的控制器在高速行駛時的穩定性.

3.1 分析確定時域權重系數

為驗證預測時域的權重系數對軌跡追蹤精確性和穩定性的影響， 選取車速60 km·h-1， 權重系數ω2取0.4， 權重系數ω1分別取0.2， 0.4和0.6進行雙移線工況仿真， 仿真結果如圖8所示.

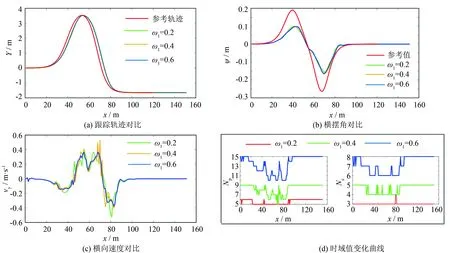
圖8 不同權重系數下的車輛狀態曲線與時域值 Fig.8 Vehicle state curve and horizon value under different weight coefficients

不同的權重系數ω1對軌跡跟蹤的精度影響不大， 當ω1取0.2時， 預測時域和控制時域較小， 控制器無法對突變軌跡做出快速響應， 車輛橫擺角和橫向車速曲線波動較大， 車輛的穩定性較差； 當ω1增加到0.4時， 控制器的跟蹤精度和穩定性并沒有明顯改善； 當ω1繼續增加到0.6時， 由圖8可看出橫擺角曲線和橫向速度曲線相對光滑， 車輛的穩定性得到明顯的改善， 且預測時域和控制時域可以根據實時車速進行自適調整， 同時在軌跡曲率較大區域， 此時橫向車速較高， 控制時域也不會太小， 保證了車輛在軌跡跟蹤時的穩定性， 同時預測時域和控制時域的大小都處于一個合理的范圍， 因此ω1設定為0.6. 在確定好預測時域的權重系數后， 對控制時域的權重系數進行分析， 同樣選取車速60 km·h-1， 權重系數ω1取0.6， 權重系數ω2分別取0.2， 0.4和0.6進行仿真分析， 最終確定權重系數ω2取0.4.

3.2 超車軌跡跟蹤仿真

為驗證所設計的自適應控制器在高速行駛時具有較好的穩定性， 將加入側偏剛度實時估計的控制器設為控制器A， 側偏剛度采用定值的控制器設為控制器B， 對比兩種控制器的軌跡跟蹤穩定性， 仿真車速由60勻加速到80 km·h-1， 參考軌跡為超車軌跡曲線， 路面附著系數為0.6(潮濕路面).

仿真結果如圖9所示， 控制器A前輪轉角變化平緩且處于合理正常范圍內， 能夠較好完成對參考軌跡的跟蹤， 而控制器B在變道超車過程中前輪轉角已經達到最大約束值(±10°)且出現較大弧度的震蕩， 已經完全偏離參考軌跡.

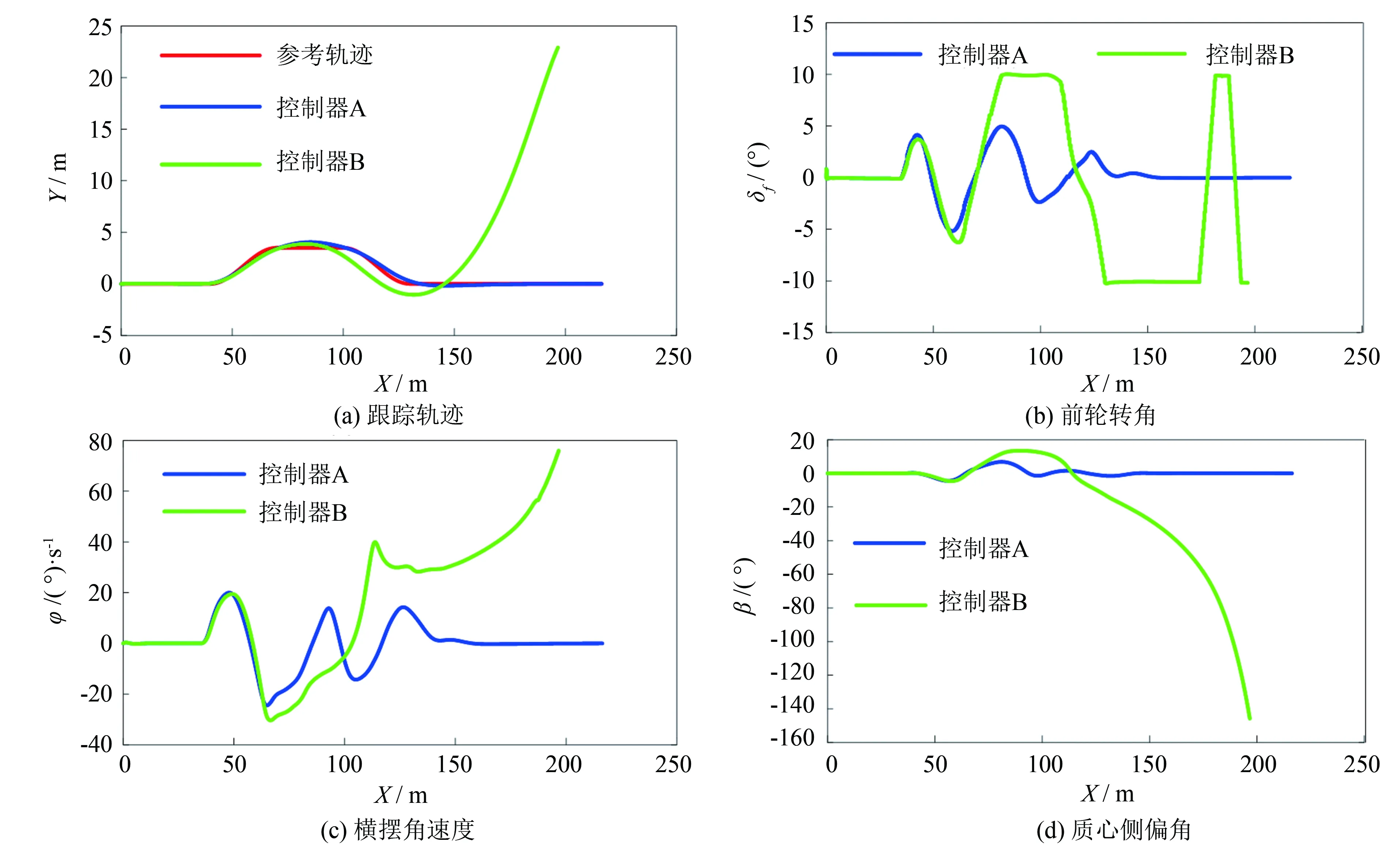
圖9 超車軌跡跟蹤仿真結果 Fig.9 Simulation results of overtaking path

同樣， 由橫擺角速度與質心側偏角曲線圖可以看出， 控制器B的橫擺角速度與質心側偏角都已經完全超出了車輛穩定行駛的穩定范圍， 表明車輛已經失去了穩定性. 這是由于控制器A對輪胎側偏剛度進行在線估計， 并將估計的參數實時更新控制器預測模型， 提高了預測模型對系統狀態量和輸出量的預測能力， 提高了無人駕駛汽車在超車過程中的穩定性. 可見， 加入輪胎側偏剛度實時估計器的模型預測控制器， 在超車過程中具有更好的行駛穩定性.

4 結語

1) 設計控制參數選擇器， 根據橫向車速和縱向車速設計模糊控制規則調節控制參數因子， 通過仿真分析確定預測時域和控制時域的權重系數， 實現了控制時域和預測時域能根據實時橫向車速與縱向車速自適應的選擇， 提高了無人駕駛汽車軌跡跟蹤的精度與穩定性.

2) 通過建立輪胎非線性數學模型， 并將其轉化為遺忘因子遞推二乘算法的標準方程， 改進了模型參數的估計方法， 對輪胎側偏剛度進行在線實時估計. 仿真結果表明， 改進的模型參數估計方法， 在中高速(75 km·h-1)行駛工況下參數的估計精度提高了32.52%， 并且提高了模型預測控制器對車輛行駛狀態的預測能力， 避免了模型參數失配的問題， 提高了車輛在高速行駛時的穩定性.