基于自適應虛擬同步發電機系統的微網逆變器控制策略研究

徐大可，盛德剛，劉亮，洪祥

（南京大全電氣研究院有限公司，江蘇南京 211106）

隨著我國節能減排政策和電力行業發展趨勢的綜合影響，分布式可再生能源并網發電贏得了大發展機遇。其中，分布式可再生能源并網的控制策略也得到了廣泛研究，其中以電壓源型換流器（voltage source converter，VSC）相關的矢量控制方法研究最為廣泛，為多端柔性直流輸電系統的遠距離傳輸提供解決方案[1-2]。然而，用矢量控制的VSC 方法策略缺乏旋轉慣性，系統易產生諧波，不能為交流系統提供穩定的電壓和頻率，增加電網運行不穩定的風險。為此，學者們給出了虛擬同步發電機（virtual synchronous generator，VSG）的控制理念，通過模擬同步發電機的慣量和阻尼特征來提高系統抗風險能力，從而保證系統電壓和頻率的穩定性。

目前，學者們對VSG 穩定性方面的研究主要在以下方面：一方面是對單臺VSG 控制直流系統的穩定性進行研究。通常的研究方法是將直流系統設定為恒功率源或恒壓源，此類系統相對來說比較簡單。文獻[2]通過利用傳統無慣性的下垂控制方法和VSG 控制的組合形式，提出了VSG控制方法的下垂控制模式。文獻[3]通過探討一種新的解耦算法，以實現VSG 來控制有功和無功獨立輸出的目的。文獻[4]通過對解耦算法的參數特性進行分析，提出了以保證系統運行穩定性為主要指標的設計方案。另一方面是對含VSG的多端直流系統進行研究。考慮到系統的復雜程度，通常結合系統穩定性分析方法進行討論。文獻[5]通過對傳統的VSG 控制策略難以快速響應直流系統注入功率的變化情況進行詳細分析，并由此提出限幅約束條件下的的VSG 控制直流系統母線電壓的下垂控制模式。為了保證復雜系統的運行穩定性，已有的文獻著重采用了模式分析和頻域分析等方法。文獻[6]結合模式分析法對交流系統運行的穩控參數進行了深入探討，以此提出促進交流系統穩定運行的參數控制優化方案。文獻[7]利用頻域分析法分析了VSG 系統的控制方式和同步電機之間的諧振作用，并提出了一種一階系統控制方案。文獻[8]提出了一種新的阻尼控制方法，并結合實驗結果論證了該方法可有效地提高系統低頻振蕩的穩定性。文獻[9]基于物理原理設計出含VSG 系統的下垂控制模式，并根據模式分析法對交流系統穩定性影響進行了深入探討。

綜上所述，對于VSG 的多端柔性直流系統的穩定性研究方面存在著以下問題：當VSG 利用直流系統電壓下垂控制后，多端直流系統中將出現新的振蕩模式，將直流系統等效為恒定功率源進行分析是具有一定局限性的。下垂控制的主要原理為通過模擬同步發電機的有功和頻率、無功和電壓之間的下垂關系，使其控制下的微源在未有高頻通信的基礎上能完成負荷分配的方式，但下垂控制方法根本上并不能解決分布式電源的慣性問題，即該組成系統仍是“弱慣性”系統［10-11］。

基于此，將根據荷電狀態調整下垂系數的方法拓展到VSG 控制之中，通過引入自適應下垂特性的概念，使用平移下垂特性的方法對VSG 控制做了進一步改進，改進后的VSG 控制減少了對系統穩定性的影響，更有利于實現有功功率的合理分配與荷電狀態的快速調整，通過Matlab/Simu?link 工具進行建模仿真，結果驗證所提自適應VSG控制策略的合理性。

1 虛擬同步發電機系統傳統的下垂控制思想

虛擬同步發電機系統傳統的下垂控制思想可大致分為3 種形式：1）利用電流變量參與控制的V—I下垂策略；2）利用功率變量參與控制的V—P下垂策略；3）利用V2—P下垂策略。其中，本文重點探討V2—P控制策略進行含VSC 換流站模型的研究。VSC 換流系統的功率平衡簡易模型如圖1所示。

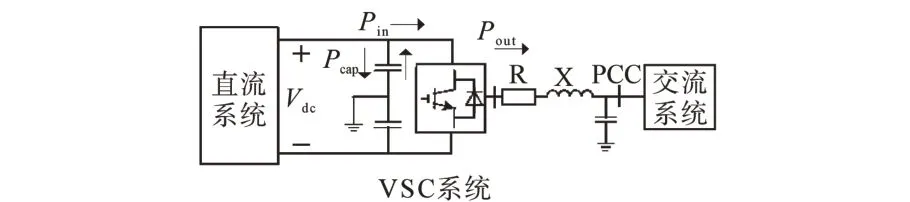
圖1 VSC內部功率平衡簡易模型Fig.1 Simple model of VSC internal power balance

圖1 中，Vdc表示換直流系統的母線電壓；Pin，Pout分別表示直流系統輸入功率和換流站輸出功率；Pcap表示直流電容存儲/釋放的功率；R，X 分別表示換流系統交流母線到公共連接點（point of common coupling，PCC）間的線路等效電阻和電抗。

建立VSC換流系統內的功率平衡方程為

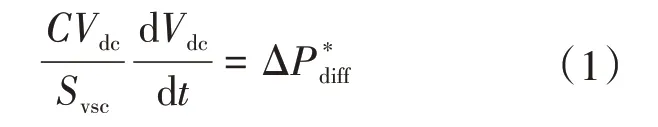
式中：C為換流系統的電容值；Svsc為換流站的額定容量。ΔP*diff為換流系統輸入輸出功率差的標幺值。

結合文獻[12]所述，V2—P下垂控制原理可如下表述：當換流站的輸入功率Pin和輸出功率Pout因擾動而失去平衡狀態時，其功率偏差可由直流電容進行補償，見式（1）。在此過程中換流站的直流電壓也將所有變化。因此，V2—P下垂控制策略選擇直流電壓的平方差作為換流站的輸入控制信號，通過計算附加輸出功率結果來調節換流站的功率輸出，保證直流系統電壓在許可范圍內運行。其所需計算的附加輸出功率見下式：

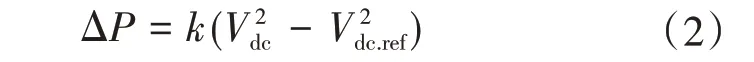
式中：k為下垂系數；Vdc.ref為直流系統參考電壓值；ΔP為換流站所需調整的參考功率。

結合文獻[13-14]闡述的d-q雙環解耦控制的原理上，本文增設下垂控制模塊，以此來建立完整的V2—P下垂控制模塊。鑒于電壓源換流器的多端柔性直流輸電系統（voltage source converter based multi-terminal direct current，VSC-MTDC）內各換流站的直流母線電壓數值上接近，可近似認為VSC-MTDC 中各換流站間的功率分配可由下垂系數k控制，其控制原理圖如圖2所示。

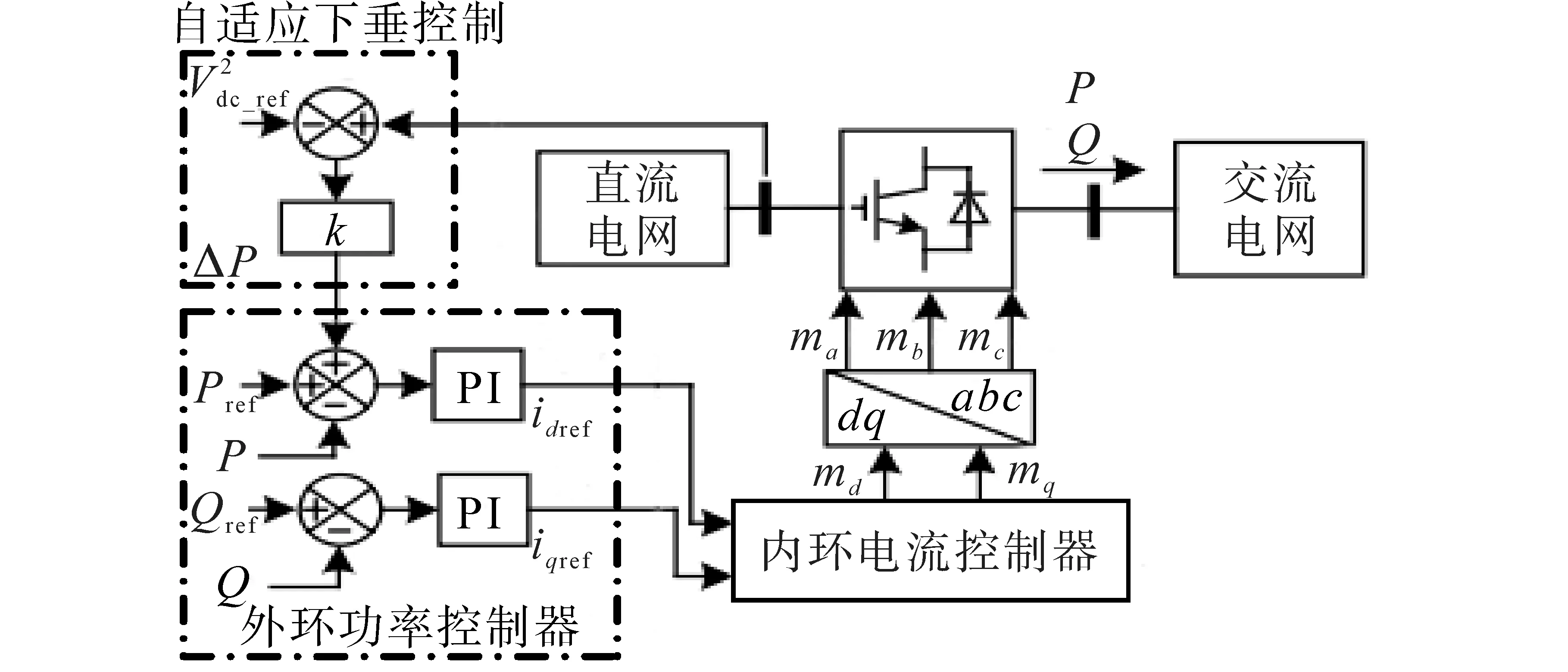
圖2 V2-P 下垂控制器Fig.2 V2-P droop controller

圖2 中，Pref，Qref分別表示換流站輸出的參考功率；P，Q分別為換流站實際輸出功率；idref，iqref分別表示d軸和q軸的參考電流；md，mq分別表示d軸和q軸的調制信號；ma，mb和mc分別表示三相調制解調信號。

2 基于虛擬調速器的虛擬同步發電機控制策略

換流站和同步發電機存在類似的功率平衡關系，如圖3所示。其中，將公共連接點作為系統的平衡參考點，設PCC 處母線電壓為U∠0°，VSC交流側母線和同步發電機側電壓均設定為E∠δ，原動機的機械功率設定為Pm，其相應的轉子動能設為Ek，同步發電機輸出的額定功率設為Pe。同步發電機的功率平衡方程可利用轉子運動方程來闡述：

圖3 換流系統和同步發電機的功率平衡對比Fig.3 Comparison of power balance between commutation system and synchronous generator

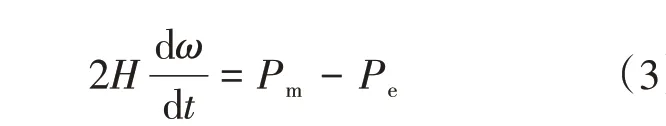
式中：H為發電機組的慣性時間常數；ω為發電機轉子的角速度。

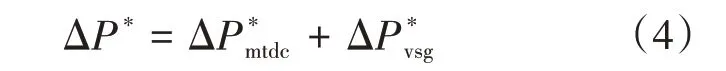
式中：Hvsc為發電機的虛擬慣性時間常數；ω*為換流站交流側實測角頻率。

當交流系統的角頻率產生變化時，控制器將產生ΔP*vsc用來調整換流站的輸出功率和補償阻尼角頻率的變化。

為求解出虛擬調速器的附加功率變化量ΔP*mtdc，需建立系統角頻率和直流母線電壓的耦合關系，對式（1）和式（3）的左側部分建立等式并計算積分[15]，則有：

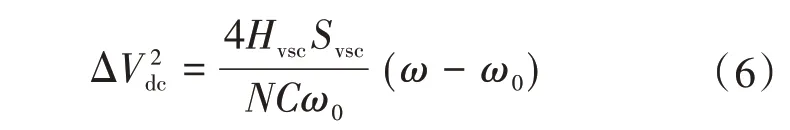
式中：N為換流站內直流系統的電容數目；ω0為系統的額定角頻率；ΔVdc為直流母線電壓的修正量。

對式（6）進行標幺化處理后，將其代入式（2）可得：

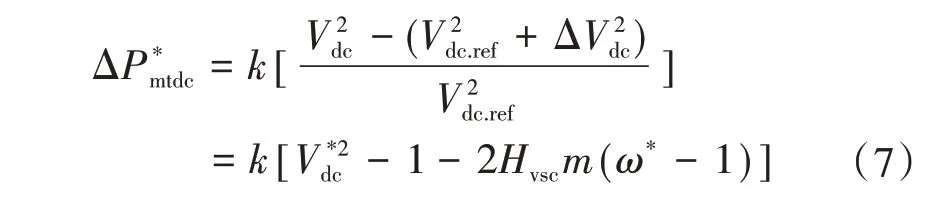
式中：V*dc為直流系統電壓的實測值；k為放大系數；m為VSC和直流電容的容量比。

m的數值為直流電容時間常數的倒數，即

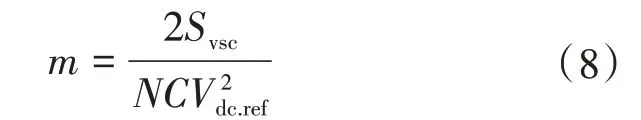
式（7）則為本文設計的虛擬調速器控制模塊，其控制原理如圖4所示。

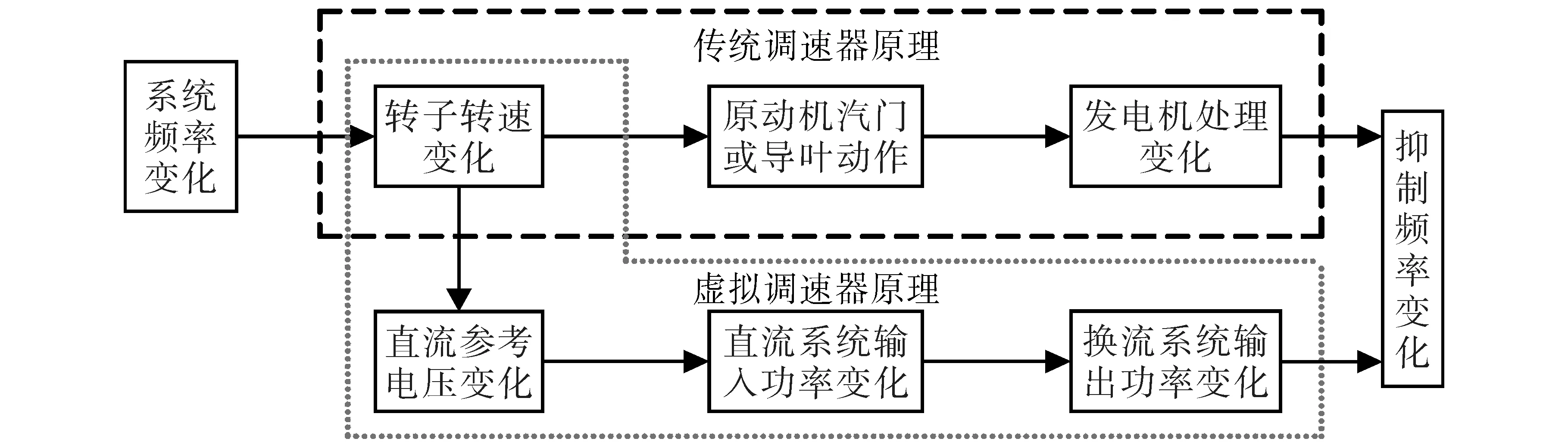
圖4 虛擬調速器原理圖Fig.4 Virtual governor schematic

結合式（7）和圖4可知，虛擬調速器可以根據交流電網的頻率變化自動對換流站的輸出功率進行調整，從而達到抑制系統頻率偏移和波動的效果。

綜上分析，虛擬轉子運動方程為

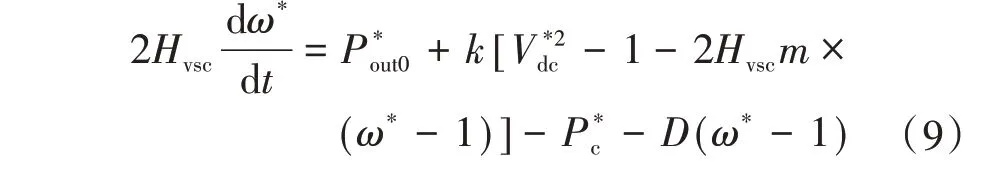
式中：P*out0為換流站輸出功率的初始值；D為虛擬阻尼系數。

設計的虛擬同步機控制器如圖5所示。

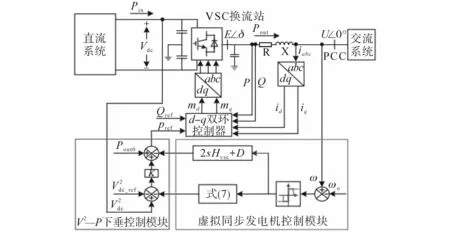
圖5 虛擬同步電機控制模塊Fig.5 Virtual synchronous motor control module

由式（9）和圖5可知，換流站的功率輸出是由直流母線電壓和交流系統頻率共同決定的，因而AVSG 控制策略可兼顧VSC-MTDC 控制系統直流電壓和電網頻率的穩定性指標。當交流系統發生擾動或故障時，AVSG 控制策略將對VSC-MT?DC 系統內各換流站的功率分配進行自動調整，并模擬出同步發電機的輸出功率，補償電網波動的頻率差并抑制系統振蕩阻尼，無需建立站間通信方式，確保直流母線電壓在合理范圍內變化，不會出現VSC-MTDC系統電壓越限的情況。

3 AVSG改進控制策略

鑒于以上探討的VSC-MTDC 模型中換流站之間的功率分配方法是按照下垂系數k進行比例控制的，結合文獻[15]所述的分段式下垂特性原理對本文的下垂控制系數進行如下改進。

將AVSG 策略中的下垂特性曲線分成含角頻率上、下限閾值[16]的水平段和含區間的斜線段兩部分，設定其斜率為k1，其值由最大頻差和發電機輸出功率綜合決定，并隨發電機出力進行相應動態調整，如圖6所示。

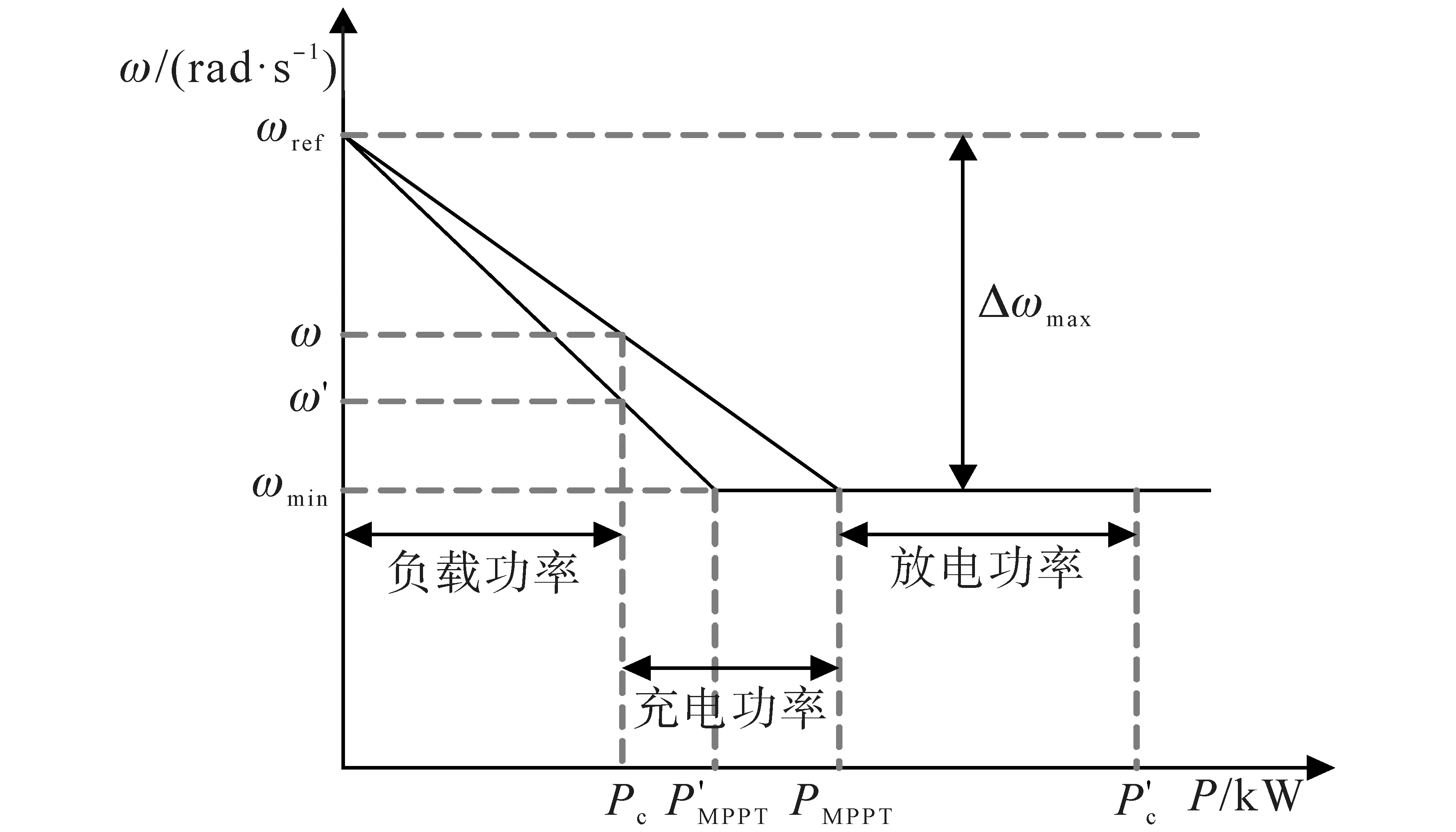
圖6 自適應分段式下垂控制特性曲線Fig.6 Adaptive segmented droop control characteristic curve

當同步發電機的輸出功率無法支撐微網系統的有功負載時，VSG 控制系統會直接調到下垂特性的水平直線段控制區間，控制直流電容放電來補充功率差額，其設計原理控制流程如圖7所示。

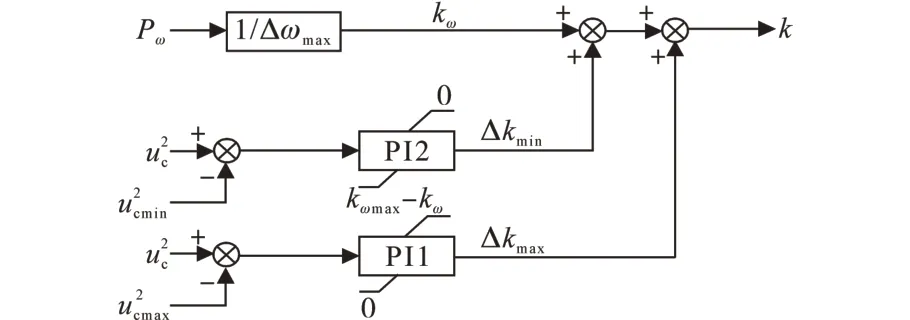
圖7 自適應下垂控制系數的AVSG模塊Fig.7 AVSG module with adaptive droop control coefficient

將風電場的輸出功率和系統角頻率偏差的最大比值設定為下垂控制曲線的對應斜率，利用VSG 系統的輸出角頻率的下限閾值ωmin設為下垂控制特性曲線的水平直線段，結合直流系統的端電壓來反映直流電容器組的荷電狀態，并分別設為直流電容器組的絕對和相對工作狀態的電壓界限閾值。

利用自適應下垂系數的AVSG 系統控制策略，根據直流電容器的荷電工作狀態，本文選取以按照下垂系數承擔負載為目標進行優化工作，其控制模式見表1。

表1 控制模式Tab.1 Control mode

3.2 自適應調整下垂特性曲線

本文建立的自適應動態調整下垂特性的控制原理如圖8 所示。當系統處于模式1 狀態下工作時，可采用分段式下垂特性曲線進行協調控制。當系統從模式1 跳轉到其他模式時，本文保持原有下垂控制曲線的斜率值，并對整個下垂控制特性曲線進行平移。

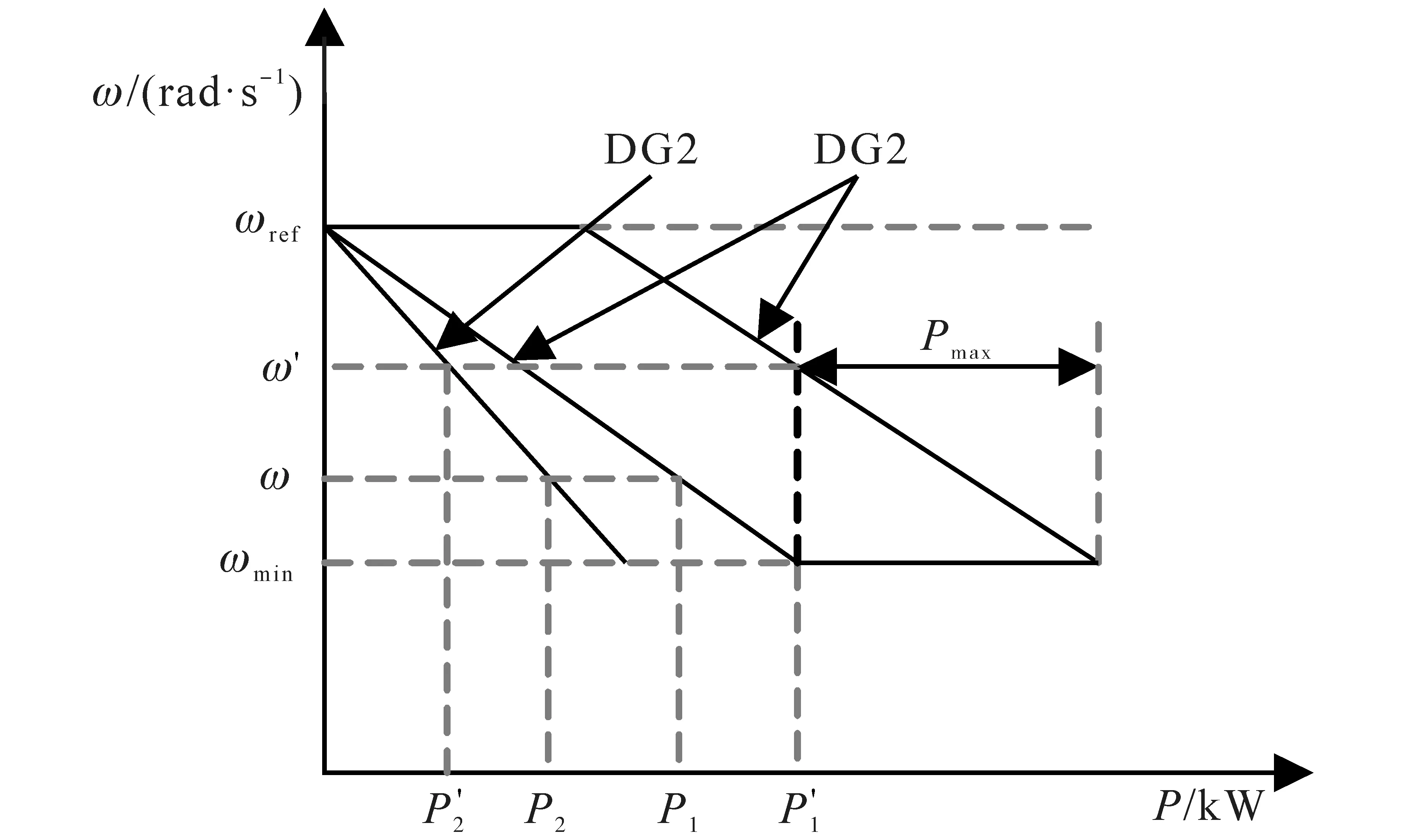
圖8 自適應下垂系數調整方式Fig.8 Adaptive droop coefficient adjustment method

如圖8 所示，在系統進入控制模式2 時，將下垂特性曲線水平向右進行平移，從而增加VSG 的有功輸出；當系統處于模式3狀態工作時，將下垂特性曲線水平向左進行平移，達到減小VSG 有功輸出的目的，由差額功率的單元提供負荷供電。采用下垂控制特性曲線水平移動的方法能夠重新調整系統運行點并合理分配有功，且能緊跟風電出力變化快速做出功率調整，從而有效避免下垂系數幅度調整過大帶來的不利影響。

4 算例分析

為驗證本文所提的基于自適應下垂控制系數的AVSG 模型的合理性，結合Matlab/Simulink仿真系統進行建模分析，模型主要包括：2個風電場、2 個風電換流站和2 個常規換流站。AVSG 系統的模型參數為：換流站額定容量450 MV·A，直流系統母線電壓220 kV，交流系統電壓110 kV，直流系統電容0.75 mF，線路電阻值0.01 Ω/km，線路電抗值0.5 Ω/km。 風電系統采用恒壓定頻控制方式，其系統模型的設計原則見文獻[17]。對于AVSG 系統模型的控制方式選擇自適應下垂系數控制方式。其中，分布式電源1有功輸出為295 MW，分布式電源2有功輸出為300 MW。風電場內配置的風電機組數目為20 臺，單臺容量設置為5 MV·A。

本文設計的自適應AVSG 控制系統主要設置四機系統和所供組成獨立電網，負荷為300 MW，系統頻率設置為50 Hz，分布式電源1 通過母線7并網，分布式電源2 通過母線12并網。模型如圖9所示。

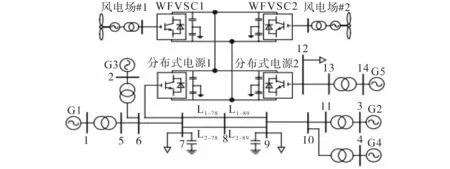
圖9 雙風電場多端送電系統Fig.9 Multi-terminal power transmission system of double wind farm

采用自適應AVSG 控制策略進行含VSC換流站模型的研究，并與傳統下垂控制方法進行對比，其優化控制響應的效果如圖10所示。

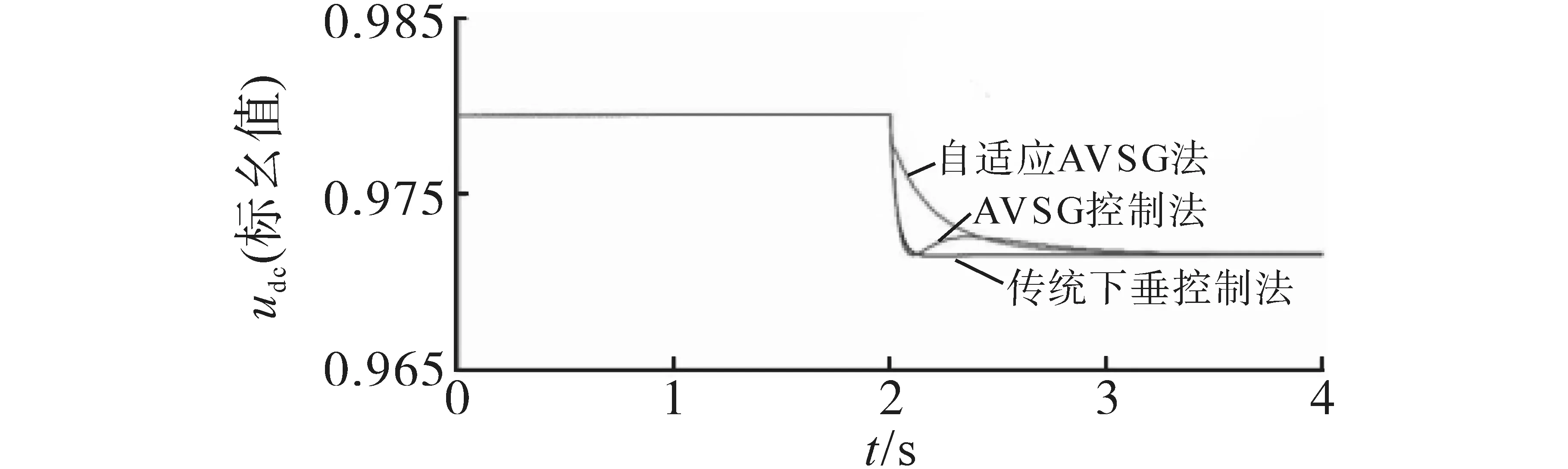
圖10 不同控制策略下直流系統電壓變化Fig.10 Voltage change of DC system under different control strategies

從圖10 可看出，根據本文不同的控制策略，為了對系統負荷變化進行很好地功率平衡，均可采取直流系統的電壓變化來進行相應調節，從而保證系統電壓調整到新的平衡態。若單獨采用傳統下垂控制的方法，考慮該方法的弱慣性特點，當系統負荷突然增加時，直流系統的電壓會迅速降低。利用本文的基于自適應下垂控制系數的AVSG 控制方法后，直流系統的母線電壓會逐漸緩慢降至新的平衡態，說明該方法增加了系統慣性。

4.1 基于自適應下垂控系數的AVSG控制效果

當風電機組無法保證系統的功率平衡時，應通過直流系統提供所需的功率缺額，設定系統負荷在46～50 kW 間隨機變化。其相應的仿真結果如圖11～圖13所示。

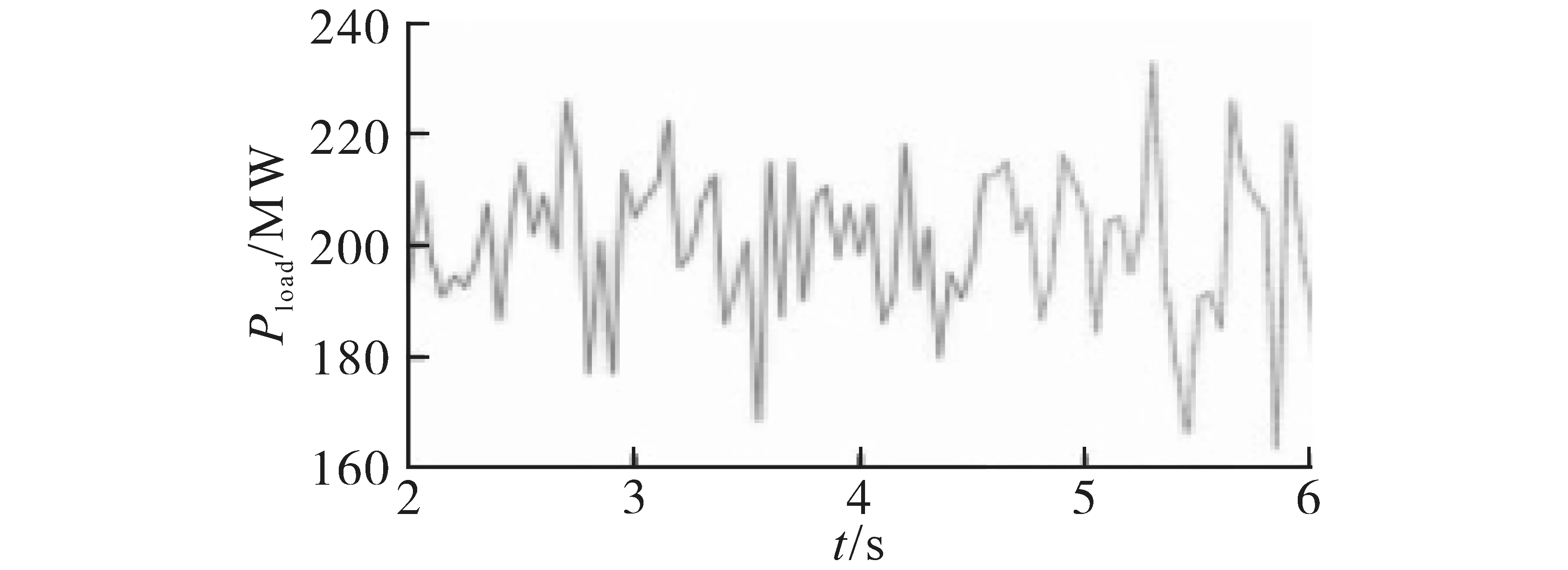
圖11 短時間內系統負荷變化Fig.11 System load change in a short time

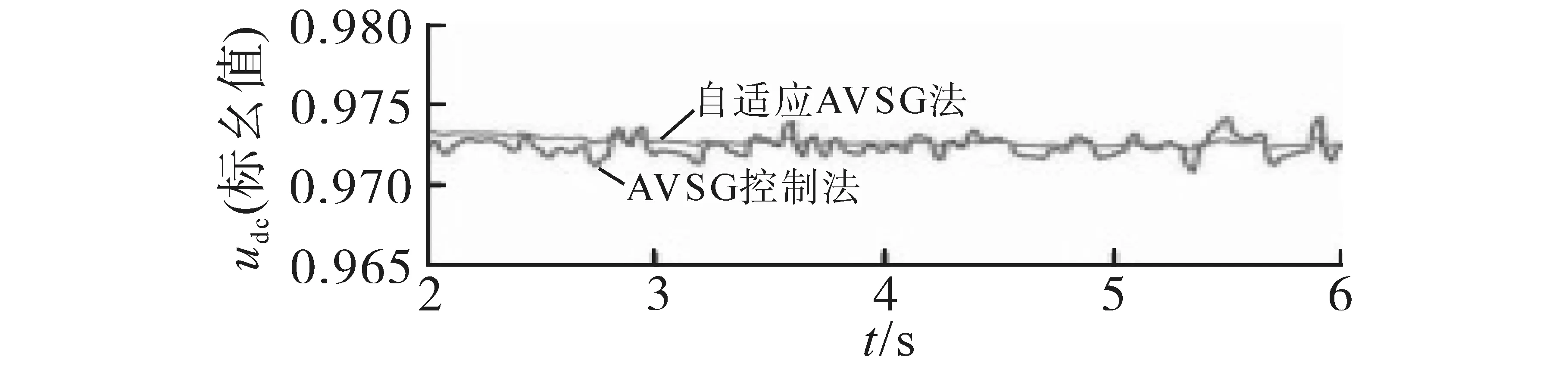
圖12 直流系統電壓響應變化Fig.12 DC system voltage response change

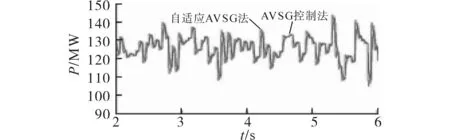
圖13 直流系統輸出功率響應變化Fig.13 DC system output power response change

從圖11～圖13 可看出，利用AVSG 控制方法時，隨著系統負荷的變化，雖可保證系統運行穩定，但系統電壓依然出現較大的波動；而采用基于自適應下垂控制系數的AVSG 控制方法后，可明顯看出，在系統負荷較大波動的情況下，直流系統電壓的質量也會得到明顯改善；且從圖13可發現，采用基于自適應下垂控制系數的AVSG 控制方法后，直流系統的輸出功率響應更迅速，所提供的功率幅值更大，因此可以減小系統的功率偏差和直流系統的電壓波動。因此所提出的自適應下垂控制系數的AVSG 控制方法可增加系統慣性，提高系統抑制電壓波動的能力，從而改善了直流系統的電壓質量。

4.2 基于自適應下垂控制系統對系統穩定性的影響

以下充分探討系統受到擾動后恢復穩定運行的情況，以此來驗證本文所提出的自適應AVSG 控制策略的合理性。在系統進行擾動試驗前，將G1～G4 的電力系統穩定器（power system stabilizer，PSS）退出，投入自適應AVSG 控系統模塊。設定線路L1-78在t=2.0 s 處發生三相瞬時故障，持續周期為5個周波時長，系統故障后恢復結果如圖14～圖16所示。

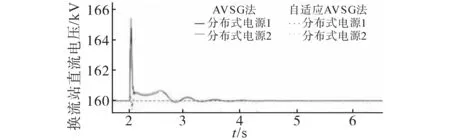
圖14 發生故障時直流系統電壓變化Fig.14 DC system voltage change in the event of a fault

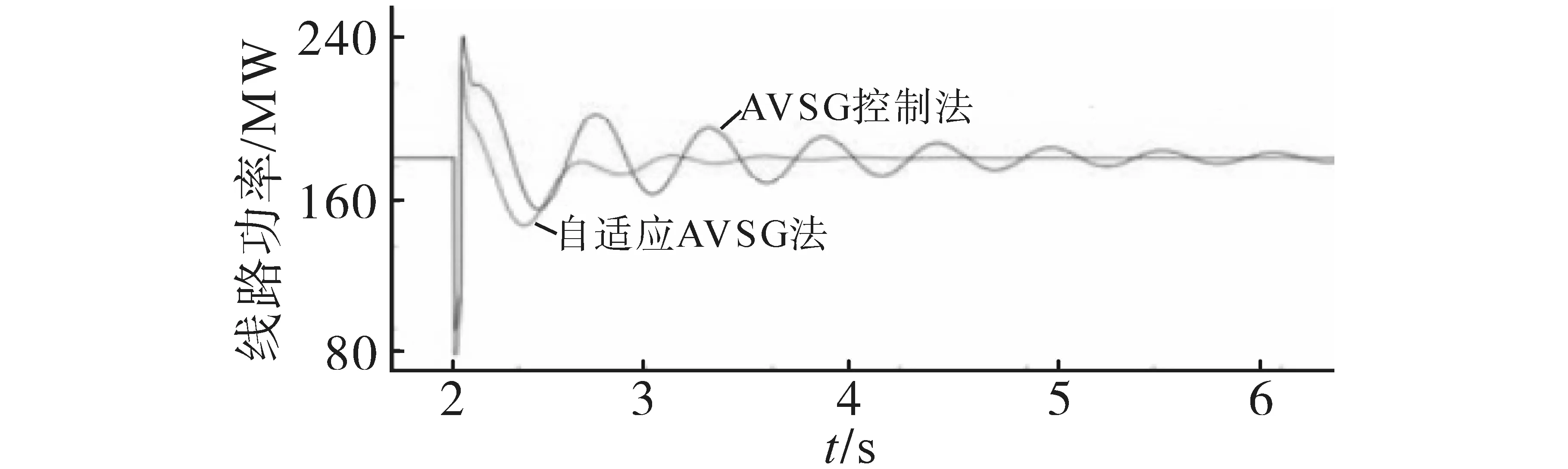
圖16 發生故障時線路功率響應變化Fig.16 Line power response change in the event of a fault

由圖14 可知，采用自適應AVSG 控制時，系統能夠在故障發生后迅速地恢復到初始穩定運行狀態上來，且直流系統的母線電壓恢復到初始狀態值。而由于交流系統抗擾動能力差的特點，使得傳輸線路L2-78上出現連續功率振蕩的情況，如圖15，直至6 s 后才漸趨穩定，但系統未能完全穩定。而采用自適應AVSG 控制策略時，直流系統的母線電壓會隨著轉子角頻率偏差自行追蹤調整。且在故障時間內，同步電機的轉子轉速會陡增，直流系統電壓也會急劇增大，利用自適應AVSG 控制模塊可迅速降低有功輸出，并結合直流系統電壓限幅的作用，直流系統最高電壓不超過1.05 標幺值，使其保持在允許范圍內。并且分布式電源2 模塊有功輸出提高，直流系統電壓會快速回落。在故障清除后，分布式電源1 的直流電壓會繼續追蹤系統角頻率進行自適應調整。因此在整個故障持續過程中，傳輸功率振蕩和發電機轉速振蕩均能被有效抑制，并在6 s 后系統恢復穩定。

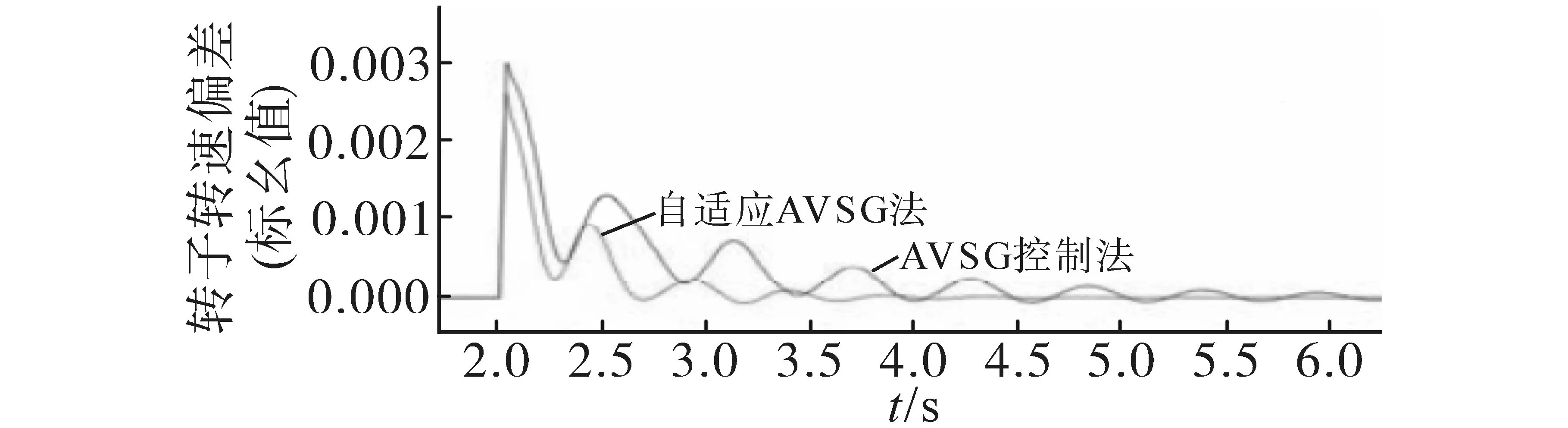
圖15 發生故障時轉子轉速響應變化Fig.15 Rotor speed response change in the event of a fault

5 結論

鑒于直流微網系統慣性低、且直流系統母線電壓抗干擾能力弱的問題，本文提出了一種模擬同步發電機特性的控制策略，并結合荷電狀態對下垂控制系數進行調整，得到了基于自適應AVSG 控制方法，根據下垂控制特性曲線的平移操作來調整虛擬同步電機有功分配方式。通過仿真結果得出，基于自適應下垂控制特性的AVSG控制策略能有效避免下垂控制系數變化過程中可能出現的系統失穩風險，有效地分配系統有功并調整直流系統的荷電狀態，從而確保風儲發電單元持續支撐含可再生微網系統的穩定運行。