巖體地質強度指標（GSI）特征分析

虞金林

（中國建筑材料工業地質勘查中心江蘇總隊，江蘇 南京 211135）

0 引言

Hoek-Brown 強度準則是Hoek 和 Brown 在基于Griffith 強度理論以及對大量巖石三軸試驗和現場巖體試驗成果的分析，于1980 年提出。

廣義的Hoek-Brown 準則還引進了地質強度指標（GSI）和巖體擾動系數（D）的概念，將巖體分級與物理指標參數有效地結合起來。

1 GSI 值定量化方法

地質強度指標是E. Hoek 提出的一種圍巖分級系統，GSI 的取值直接與巖體力學參數相聯系，因此GSI 圍巖分級與Hoek-Brown 強度準則的聯合使用在工程實踐中更具有可操作性，能夠方便、及時、準確地反映巖體的實際情況。

通過充填程度Rf、風化程度Rw與粗糙度Rr之和確定GSI 體系中結構表面條件SCR， 可參見Sonmez[1]等的研究確定取值評分表，見表1。

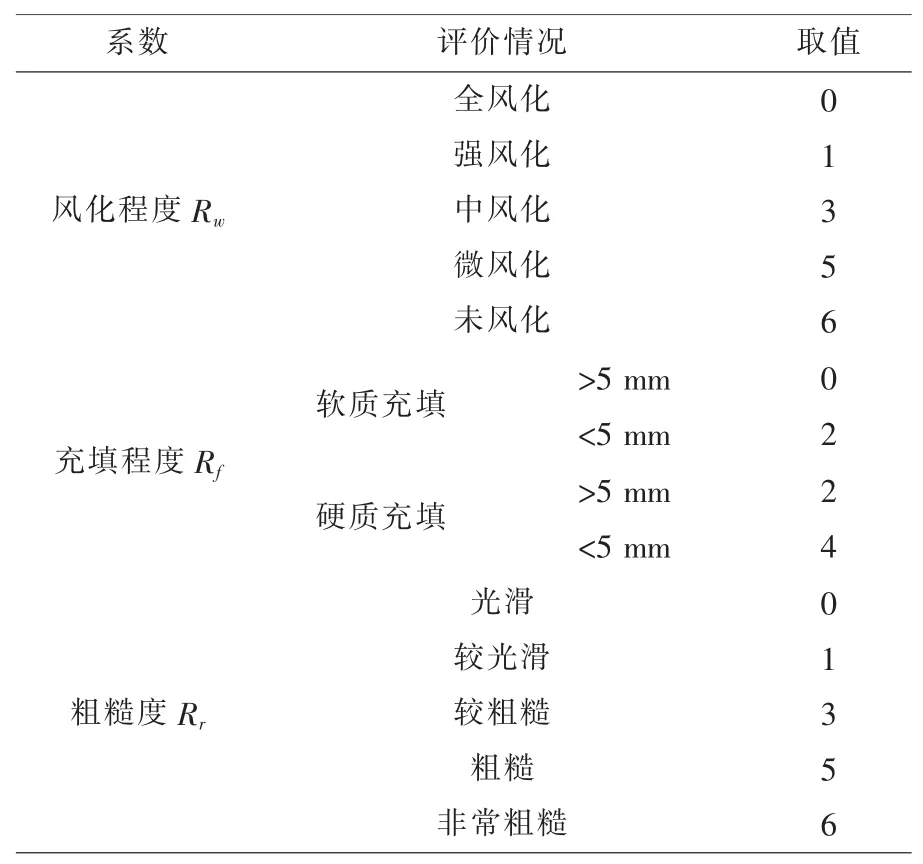
表1 結構（節理）表面條件（SCR）評分

可量化結構表面特征， 將結構表面條件SCR（0～18）分為 5 個等級。

GSI 體系中巖體結構等級SR 的計算公式如式（1~3）所示：

當巖體為塊狀或完整結構（I/M）時，有：

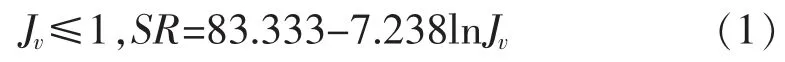
當巖體為散體結構（D）、碎裂結構/擾動/裂縫（B/D/S）、鑲嵌結構（VB）、塊狀結構（B）時，有：

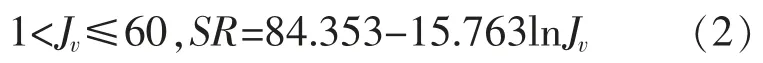
當巖體為層狀/剪切帶（L/Sh）時，有：

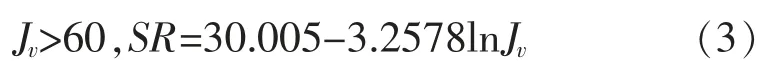
GSI 體系中根據粗糙度Rr、 風化程度Rw與充填程度Rf之和確定了結構表面條件SCR， 基于對巖體結構特征進行區間值量化需采用SCR、SR，則在巖體三維節理面網絡基礎上得到巖體結構等級SR 和巖體體積節理數Jv。 相關GSI 定量化表格如圖1 所示。

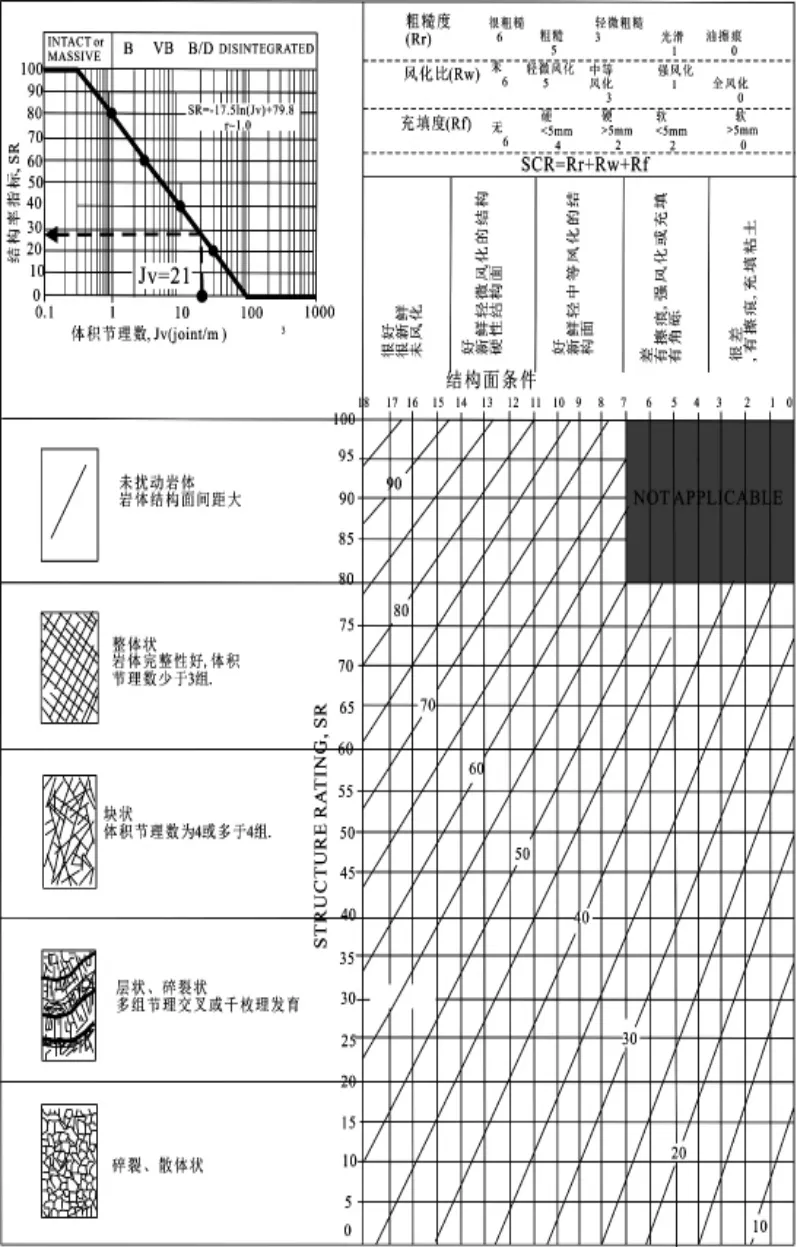
圖1 改進的GSI 定量化

Hoek-Brown 強度準則中巖體力學參數取值對GSI 的取值很敏感[2]，需要對GSI 的取值做到更加量化和精準。 RMR 是國際常用的巖體分級方法，其數值與[BQ]等具有一定的關系，而Hoek 等通過將GSI與RMR 聯系起來， 使得GSI 的取值具有了普遍適用性。 RMR 估算 GSI 的具體表達如式（4）所示[3]：

RMR 的值可以用現場巖體特征根據RMR 分級方法進行計算，也可以根據已知的[BQ]進行換算。 大量的實測資料統計分析表明，[BQ]值與RMR值呈線性關系[4]，具體使用時可采用擬合的關系如式（5）所示：

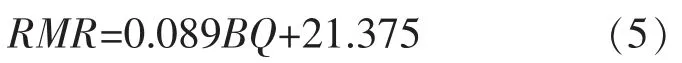
2 實例分析

根據徐州市銅山區柳泉鎮楊山研究區邊坡坡向，邊坡類型大致分為五段，每段巖體中的結構面選取相應的層面及共軛節理面作為主控結構面進行分析。 巖體結構面間距總體上為70~100 cm，巖層厚度以中厚層為主，且巖體結構面一般處于閉合狀態，無充填，結合較好。因此將巖體定性為塊狀或厚層狀結構，巖體的完整程度應為較完整狀態。

楊山五段邊坡巖體的GSI 值采用定性與定量相結合的方法。 根據現場地質調查，每段邊坡巖體均發育有結構面，其中以節理面居多。 本研究利用SCR、SR 對巖體結構特征進行區間值量化，通過改進的GSI 定量化表格確定GSI 值， 對比采用RMR值間接計算GSI 值， 結果見表2， 計算所得的GSI值基本均在通過GSI 定量化表格所確定的GSI 值區間范圍內，這表明兩種方法分析結果是一致的。

利用對應GSI 量化表用插值法確定GSI 主要依據野外巖體露頭的觀察和測量，然后對應GSI 量化表用插值法取值，屬于直接法確定GSI。 這種方法雖簡單快速、使用方便，但卻具有很大的主觀性和經驗性， 且所得值具有一定的區間性， 不利于GSI 系統的普遍使用。 對比GSI 定量化表取值，采用RMR 值間接計算得到GSI 值指標是確定的、唯一的，方便了巖體穩定評價中參數的選取，對分析邊坡穩定性以及后續開挖方案設計具有重要的參考意義。

3 GSI 值修正方法

GSI 值的一種表現形式是利用RMR 值， 在邊坡開挖中，要考慮地下水和結構面產狀對其產生的影響基礎上來進行RMR 的取值。

巖體與節理面的蝕變作用和風化作用及地下水對巖體力學性質弱化作用等，對巖體力學性質的影響存在不同的差異。

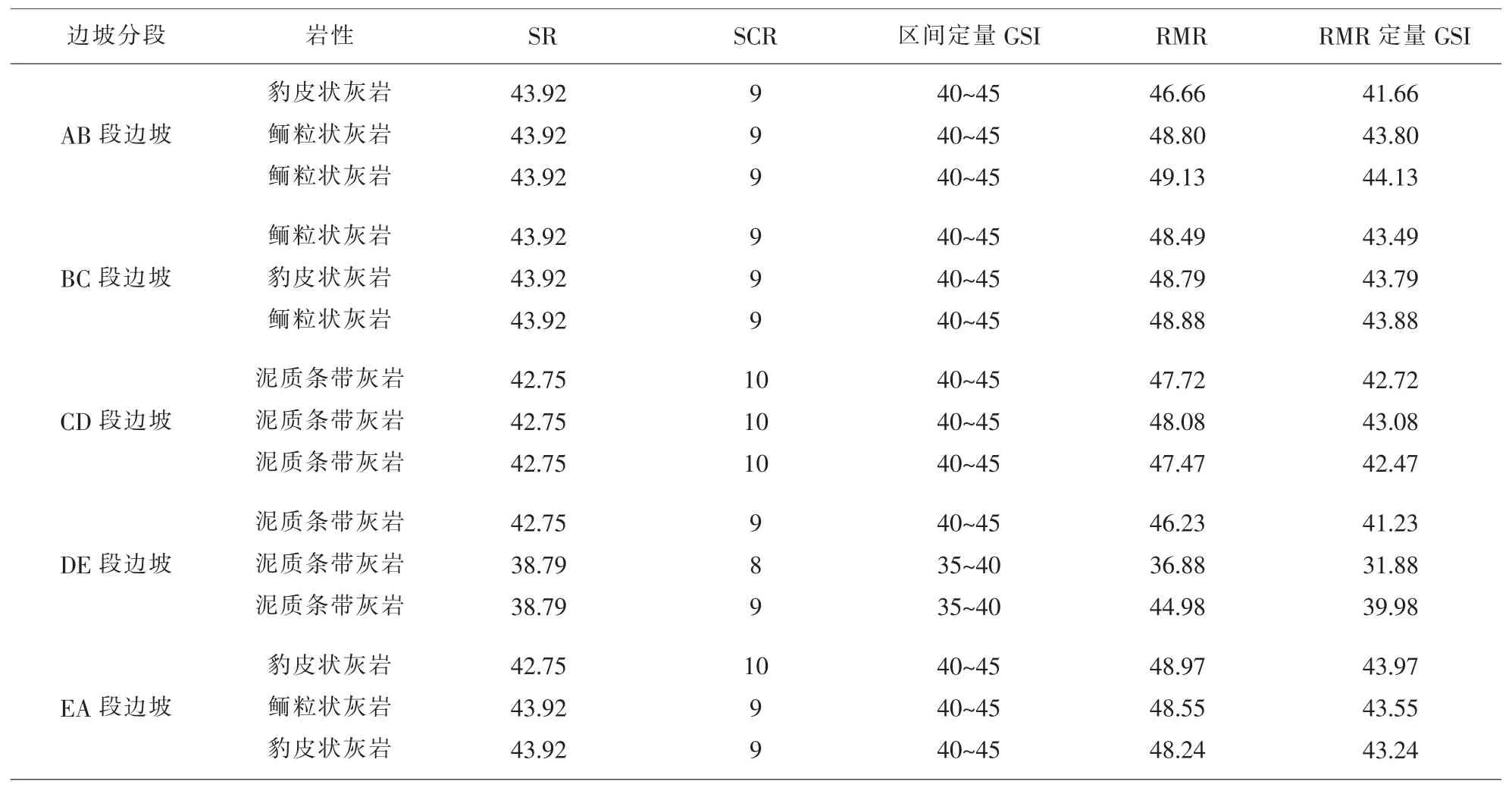
表2 GSI 值確定法對比

黃達[5-6]等提出了結構面產狀修正評分表，該表針對RMR 體系中結構面產狀及其分類進行評分，見表3，α 為邊坡走向與節理組走向的夾角；β 為節理組傾角。 非常有利時R1=0，非常不利時R1=15。

地下水對巖體力學性質的影響按照地下水的影響沒有時R2=0，很大時R2=15，見表4。

表3 結構面產狀修正評分

表4 地下水影響修正評分

修正參數Jm是根據表3、4 對現場巖體進行評分所求之和。 GSI 值的修正式如式（6）所示。

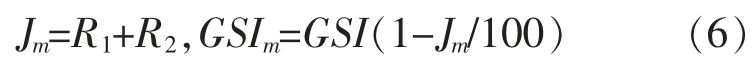
楊山五段邊坡巖體的GSI 值根據GSI 值修正方法進行了修正，依據水文地質條件所得地下水修正評分值R2與通過結構面產狀計算各巖體的結構面產狀修正評分值R1相結合。 計算結果見表5。

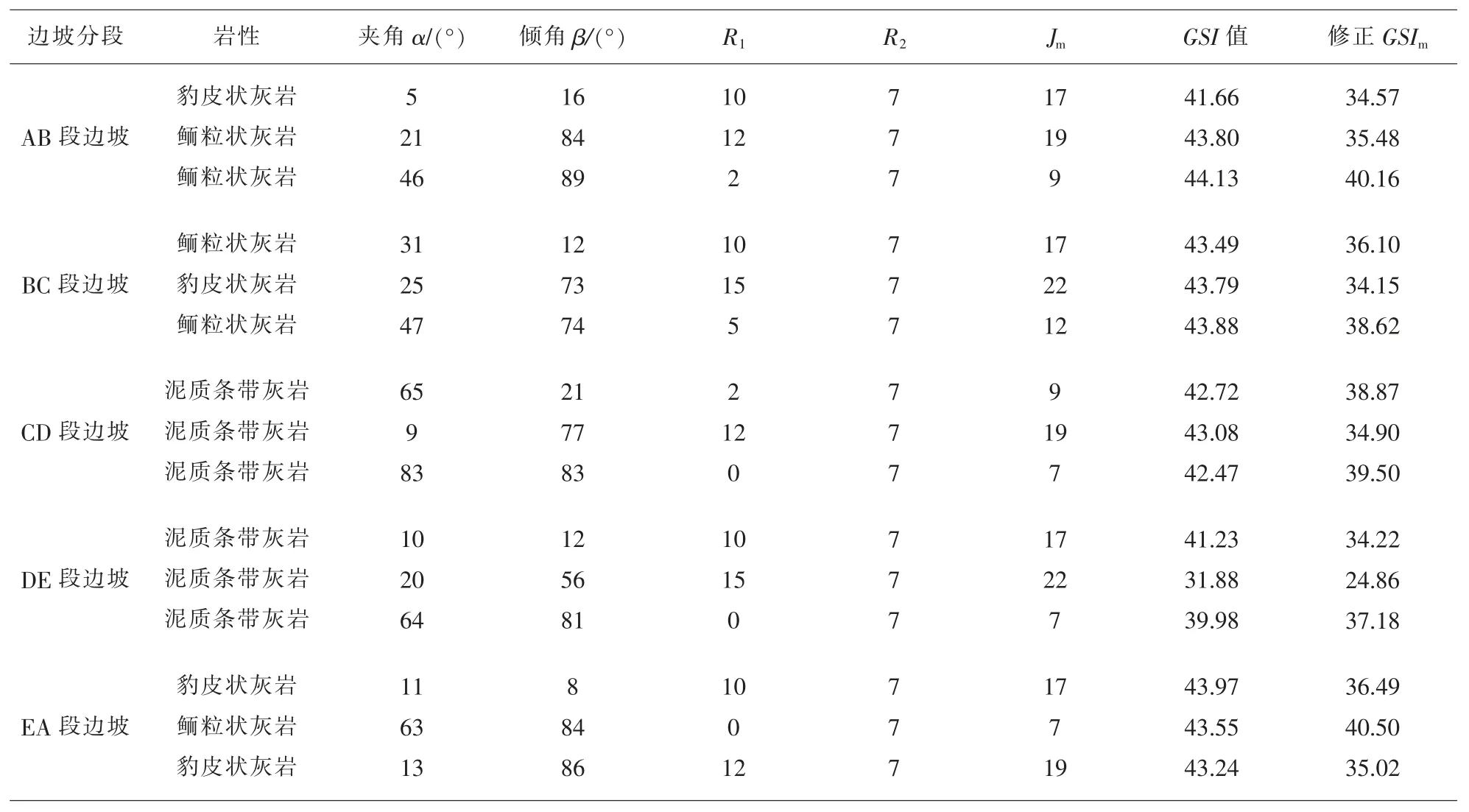
表5 巖體的GSI 修正評分值

根據表5 可知，受結構面產狀及地下水情況的影響， 修正后的GSI 值比正常的GSI 值減小了7%～22%不等。

4 巖體力學參數確定

Hoek-Brown 準則下的巖體強度參數的取值除了對GSI 的確定， 還有對均質巖塊指標mi和擾動系數D 的確定。 mi的取值與巖塊的種類和結構面粗糙程度性質有關，Rotlab 軟件中給出了mi的確定方法，表6 列出了部分相關巖體mi的取值范圍。

表6 常見巖塊的巖石指標mi 的經驗取值

擾動系數D 的取值與爆破以及應力釋放的程度有關，重載爆破破壞和覆巖卸壓引起的應力解除都會引起巖體的擾動，不同坡度（平面內）產生的側向約束對其擾動程度也有影響。 擾動系數D 的取值對巖體力學參數的確定具有很大的影響。

楊山邊坡巖體在開挖中主要由生產爆破加機械開挖的方式，局部區域爆破時所造成的破壞能延伸2~3 m，因此邊坡巖體擾動系數建議取值為0.8。

通過將Hoek-Brown 強度準則和Mohr-Coulomb 強度準則進行數據擬合，使在 σt＜σ3＜σ′3max范圍內， 兩個強度準則所對應的曲線覆蓋面積相等，如圖2 所示，最后得到基于Mohr-Coulomb 準則的等效參數。

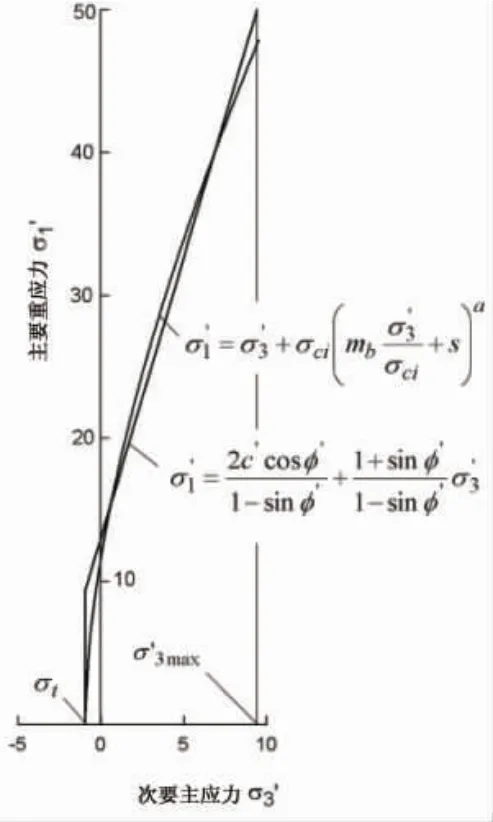
圖2 計算模型示意

Mohr-Coulomb 準則下巖體的物理力學參數都可以通過Hoek-Brown 準則來轉換，RocLab 軟件提供了一個方便的計算途徑， 不僅可以將Hoek-Brown 準則下的參數直接轉換為常用的Mohr-Coulomb 準則下的巖體力學參數，而且可以瞬時在σ3-σ1坐標系中繪出兩種強度準則的巖體破壞包絡線。 根據相關Hoek-Brown 準則的巖體力學參數數據，利用RocLab 軟件可以計算出楊山邊坡各地層分層Mohr-Coulomb 準則下的巖體力學性質指標。 為了方便GSI 法與BQ 工程巖體分級法的對比，現將兩種方法所確定的結果歸納于表7。

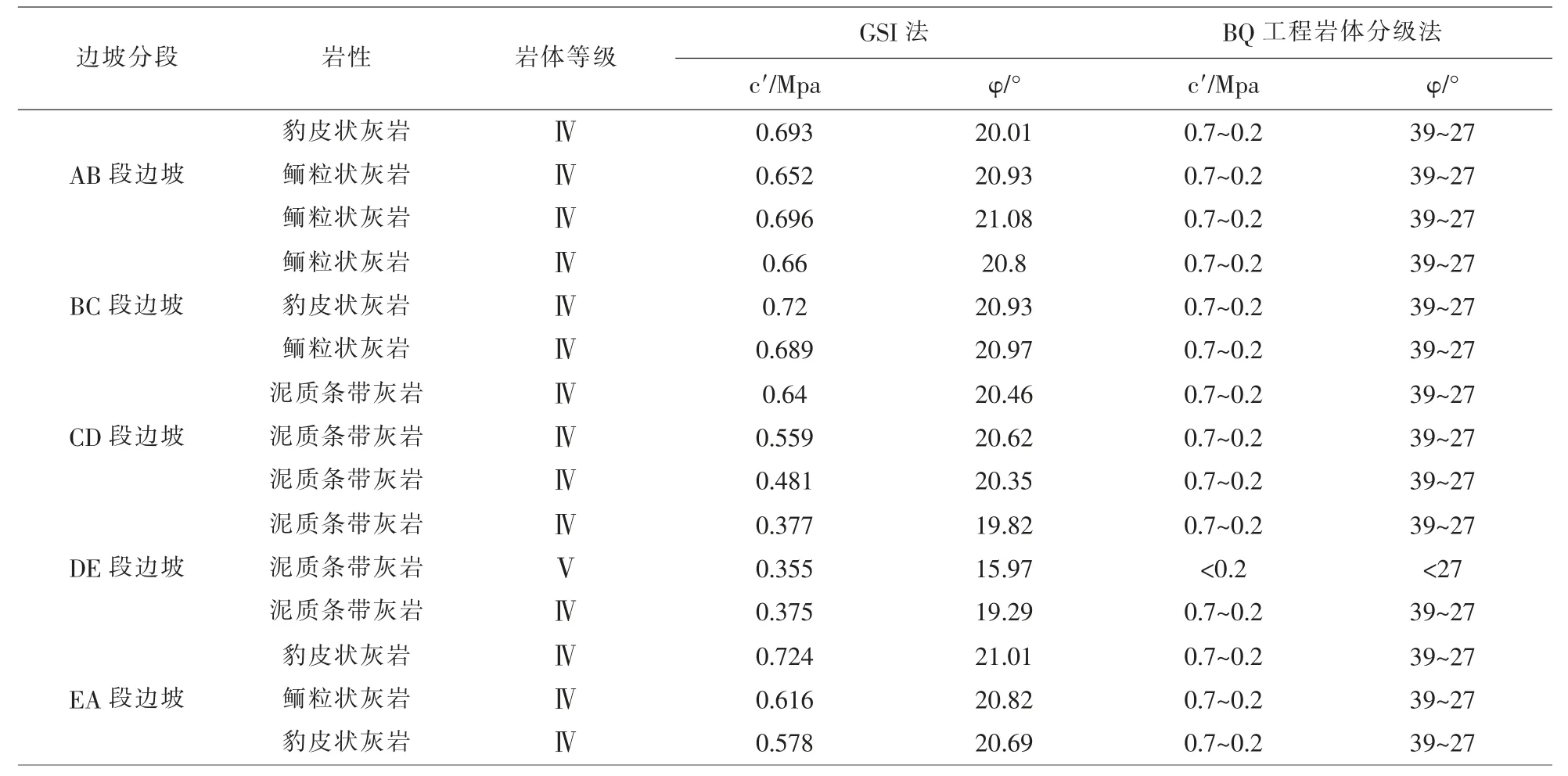
表7 研究區邊坡巖體力學參數值

根據GSI 法計算結果， 各分層巖體基本力學參數指標c＇ 值基本都處于BQ 工程巖體分級法所給出的取值區間內，但φ 值均處于BQ 工程巖體分級法所給的取值區間之外。 這主要是該區域巖體裂隙較發育，且裂隙內多為砂泥質充填，導致巖體地質強度指標GSI 值偏低， 使得巖體力學指標值與BQ 工程巖體分級法的區間值有所不同。整體上看，GSI 法確定的巖體力學參數指標很好地反映了該邊坡巖體的物理力學性質。相比于BQ 工程巖體分級法所給的取值區間，GSI 法計算得到的指標值是確定的、唯一的，可以較為便利地選取同一巖性的巖體相關力學參數指標加以計算， 方便了巖體穩定評價中參數的選取， 對分析邊坡穩定性以及后續開挖方案設計具有重要的參考意義。