深度研讀教材策略之二：再現數學知識的形成過程(1)

張強 馬騰飛

【導讀】

“雞兔同籠”在各版本教材中出現在了不同的年級：2006年人教版數學教材中，該內容出現在六年級上冊，側重讓學生學會利用方程解稍復雜的實際問題。2009年浙教版教材中，該內容出現在三年級下冊，側重讓學生利用畫圖的方法解決問題。2013年教育部審定版教材中，該內容出現在四年級下冊，側重培養學生利用假設法這一重要數學思想方法解決實際問題。

本案例中，來自昆明市盤龍區拓東第一小學的張強老師，在周佳泉老師的悉心指導下，大膽嘗試用假設法指導學生自主探究，力求完整演繹學生發現“雞兔同籠”問題數學本質的過程。沒有方程的“加持”，學生能順利“通關”嗎？讓我們拭目以待：

【案例】

課堂實錄：

一、開門見山，引出課題

1.先出示雞和兔的圖片。

師：雞有幾只腳？兔有幾只腳？

2.再出示課本第104頁例1，請學生讀題，說一說題目的意思。

師：這道問題和以前我們學過的問題有什么不一樣的地方。

……

二、化繁為簡，主動探究

（一）降低起點，初步感知

師：雞兔同籠，有8個頭，有26只腳。雞和兔各有幾只？

（師帶領學生梳理數學信息和問題并板書）

師：猜一猜有幾只雞，幾只兔？

（短暫的寧靜之后……）

生1：我猜可能有1只雞和7只兔。

……

師：大家猜測的這些情況，都是把兩種動物的頭數猜對了。但是腳的只數對不對呢？該怎么驗證？

……

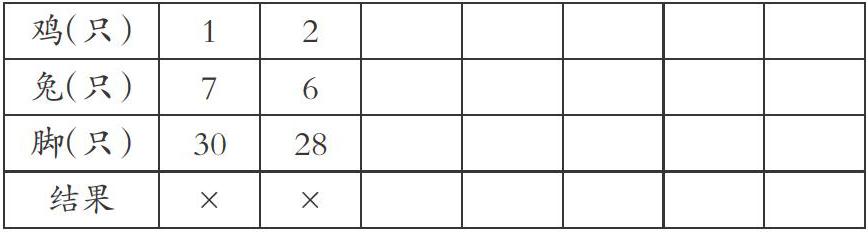
師：我們可以用表格記錄出大家猜測的情況，再計算出腳的總只數，判斷一下對不對。（出示下表，學生填寫并判斷）。

師：現在找到正確結果了嗎？

生（齊）：找到了，是3只雞，5只兔。

（二）觀察變化，感受趨勢

師：請仔細看大家填寫的表格：從左往右看，有什么變化規律？

生1：雞的只數變多，兔的只數變少，腳的只數在逐漸減少。

師：為什么腳的總數在減少呢？

生2：因為兔減少了，雞增多了。

生3：兔“換成”雞以后，腳的總數“損失”了。

師：說得真好！那么從右往左看呢？

……

師：是的，總數一定的時候，雞增加了兔就減少，雞減少了兔就增加。在雞兔“互換”的過程中，把雞換成兔腳的只數就會增加，把兔子換成雞腳的只數就會減少。

（三）深入研究，理解規律

師：如果我們一來就采取“對半”猜的方法，假設是有4只雞和4只兔子。腳的總只數和題目有什么矛盾呢？

生1：腳的總只數少了2只。

師：這時我們應該增加什么？減少什么？

……

師：增加一只兔應該增加4只腳才對呀！怎么只增加了兩只腳呢？

生2：因為你這里進來了1只兔，增加了4只腳，可是又出去了1只雞，又減少了2只腳，就相當于只增加了2只腳。

……

師：我們發現：把一只雞換成一只兔，腳的只數就增加2只;反過來，當我們把一只兔換成一只雞的時候，腳的總只數就會減少2只。當我們的猜測與實際不符合的時候，就可以根據腳的多少來判斷是哪種動物猜多了（或是猜少了），應該怎么調整。

（師帶領學生繼續觀察其他各列情況，找到調整方法）

……

（四）簡化思路，建立模型

師：能不能一來就假設全部是雞呢？

生1：不可以。因為題目中說了既有雞又有兔，這樣假設是不對的。

生2：也可以的，根據假設來判斷腳的只數不對，再調整。

師（問生1）：你同意他的說法嗎？

生1（想了想）：同意。

師：按照第二位同學的說法，我們假設全部是雞，腳的總數肯定會怎么樣？

……

師：我們可以用畫圖的方法來解決。

（師示范簡筆畫，學生模仿）

我們可以用這樣的方式就表示了8只雞，現在一共有幾只腳了？

生（齊）：16只。

師：與真實的腳數相比，還差幾只？

生（齊）：還差10只。

師：那就需要“變”出幾只兔子來？

……

師：是這樣嗎？我們來畫畫試試。

（師示范畫第一只雞“變”兔，學生模仿并完成）

師：誰來說說剛才的思路？

生：……

師：能用算式表示嗎？

（邊回顧思考過程，邊用算式表示）

師：假設全部是兔子可以嗎？

生（齊）：可以！（師帶領學生一起解答）

方法一：假設全是雞

腳：8×2=16（只）

矛盾? 總腳數相差：26-16=10（只）

雞與兔腳數差：4-2=2（只）

調整? 雞換成兔：10÷2=5（只）

雞還剩：8-5=3（只）

驗證：3×2+5×4=26（只）

解決問題? ?答：雞有3只，兔有5只。

方法二：假設全是兔

腳：8×4=32（只）

矛盾? 總腳數相差：32-26=6（只）

雞與兔腳數差：4-2=2（只）

調整? 兔換成雞：6÷2=3（只）

兔還剩：8-3=5（只）

驗證：4×5+2×3=26（只）

解決問題? ?答：雞有3只，兔有5只。

三、鞏固拓展，靈活運用

師：在現實生活中，會有人真的把兔子和雞關在同一個籠子里邊嗎？

生（齊）：不會！

師：是的，“雞兔同籠”問題其實是研究兩個互相影響的數量的變化問題。

其實在我們的生活中，這樣的問題還真不少呢。（課件出示題目）

“好又來”早點鋪的大碗米線每碗10元，小碗米線每碗8元。星期六早上才10分鐘的時間，就賣出了20碗米線，收入176元。其中有幾碗大碗米線和幾碗小碗米線？

（學生獨立完成，然后組織訂正）

四、整體回顧，提煉升華

今天，我們通過“大膽假設——發現矛盾——調整假設——解決問題”四個步驟，成功地解決了“雞兔同籠”問題。

【思考】

本節課，是昆明市盤龍區周佳泉小學數學名師工作室的全體成員，在周老師指導下進行深度研讀教材、集體備課形成的集體智慧結晶，最后由盤龍區拓東第一小學的張強老師執教演繹。

這節課最顯著的特點是讓學生經歷了知識形成的完整過程，在充分感知的基礎上逐步抽象、歸納，建立數學模型。“大膽假設—發現矛盾—調整假設—解決問題”的思維形成過程連貫、完整，具體表現在以下四個方面：

1.從不知所措到若有所悟。“雞兔同籠”問題是我國古代數學名著《孫子算經》中的經典問題，它以“雞兔同籠”事件為載體，研究互相影響的兩個變量之間的關系。對于小學生來說，第一次面對兩個不確定的數量（并且互相影響），要在同一個問題里求出兩個未知量，思維難度是極大的。所以當老師提問“你猜會有幾只雞？幾只兔？”的時候，全班出現了短暫的“寧靜”。當第一個學生的發言打破沉默之后，學生們紛紛回過神來——一共有8個頭，說明雞和兔的總數量是8，假設一部分是雞，另一部分就是兔——這不就是一年級學的“8的分與合”嗎？到這里，學生邁出了通向成功的第一步。

2.從有限窮舉到發現規律。只是猜對了頭數還不行，腳的只數也要湊足。在教師提供表格的幫助下，學生通過計算驗證自己的猜想。雖然幾分鐘過后，大部分學生都能猜出正確的答案，但是這種有限窮舉的方法其思維水平是較低的。怎樣引導孩子從低階思維向高階思維發展？這是本節課教師所要面對的一大難題。在教師的引導下，學生觀察表格中的數字變化發現了三個重要規律：一是兔和雞的只數此消彼長——因為總數不變，雞的只數增加了，兔的只數必然就減少，反之亦然;二是兔數量增加的時候，腳的總只數增加，兔數量減少的時候，腳的總只數就減少;三是把雞換成兔子，每換一次就增加2只腳，反之則每次減少2只腳。發現了這三個重要規律，就為后面“發現矛盾—調整假設”的戰略實施提供了堅實的思想基礎。

3.從表面現象到內部本質。如果用代數思維來表達本課中“雞兔同籠”問題的本質，其問題結構可以如下圖所示：

設其中一個量為x，另一個量就為（8-x），代入上式就能列一元一次方程解答;設其中一個量為x，另一個量為y，根據題意，就能列二元一次方程組解答。但是四年級的學生還沒有接觸過方程，顯然只能依靠算術思維來解決這個問題。這時候“極端”假設就應運而生，浮出水面——我們能否假設全部是雞呢？明知假設不對，仍然“姑且信之”，隨后果然“發現矛盾”，必然“調整假設”，最終“解決問題”。這四步走下來，可謂是大刀闊斧、酣暢淋漓。四年級的學生何嘗經歷過這樣的陣仗？但是依托畫圖、“復盤”、算式表達等形式，大部分學生在思維水平上得到了質的飛躍——原來看似不確定的復雜問題，可以先大膽假設，然后根據矛盾進行調整就能解決問題。這就是這節課的數學模型，也是這節課的核心價值所在。

4.從經典趣題到生活實際。小學生的思維特點是以具體形象思維為主。因此，大部分的數學問題都應該以小學生所熟悉的生活事件作為載體來呈現。“雞兔同籠”問題也不例外，它是以“雞和兔關在同一個籠子里”這樣形象生動的比喻，來承載兩個變量互相影響的數量關系，絕非某些藝術家諷刺的“只有發神經的人才會把雞和兔關在一個籠子里”。既然“雞兔同籠”只是一個問題載體，那么這類問題在生活中必然有它的原型。本案例中，張強老師用學生熟知的“大碗米線”和“小碗米線”的價錢問題，讓學生把“雞兔同籠”的問題框架回歸現實，讓學生深切地體會到“雞兔同籠”問題是真實存在于現實生活中的。用所學數學知識解決現實生活問題，凸顯數學的工具性與實用價值，這也是新課標所倡導的課改方向。

學生的數學思維發展是一個從具體到抽象、從簡單到復雜、從現象到本質的漸變過程。面對以思維訓練為主的教學內容，我們只有讓學生經歷思維發展的完整過程，亦即知識形成的完整過程，才能讓學生的思維發展步步落實，最終攀上頂峰。