不同耦合介質爆破爆炸能量傳遞效率研究*

李 桐，陳 明，葉志偉，盧文波，魏 東

（1. 武漢大學水資源與水電工程科學國家重點試驗室，湖北 武漢 430072；2. 武漢大學水工巖石力學教育部重點試驗室，湖北 武漢 430072）

鉆爆法是巖體開挖的主要手段，如何實現爆炸能量的高效利用和爆破危害效應的有效控制是工程爆破技術的研究熱點[1]。工程實踐和研究表明[2-3]，徑向不耦合裝藥爆破能有效降低孔壁峰值壓力，減少粉碎區范圍，改善爆破效果，提高爆炸能量利用率，較耦合裝藥爆破優勢顯著。而空氣和水是工程爆破中炮孔壁和炸藥間常見的兩種耦合介質，因其物理性質及動力學特性不同，對爆炸能量傳遞及爆破效果的改善也存在差異。

目前，爆炸應力波動態作用以及高溫高壓爆生氣體準靜態作用聯合破巖是巖體爆破破碎主流觀點，即爆炸能量分為沖擊波能及爆生氣體能，炸藥能量通過做功傳遞給巖體，沖擊波能主要消耗在粉碎巖體、形成初始裂隙以及誘發巖體振動方面，爆生氣體能則耗散于爆腔及初始裂隙的擴張、破碎巖體的拋擲[4]等方面。Brinkman[5]通過套管試驗，觀察了模型在爆炸沖擊波或爆生氣體單獨作用下的破壞特征，證實了爆破巖體破裂是由爆破沖擊波能和爆生氣體能綜合作用產生的。Livingston[6]通過爆破漏斗試驗，總結提出了炸藥在巖體中爆破后能量的幾種存在形式，主要包括彈性變形能、沖擊破裂能、破碎能、拋擲能及空氣沖擊波能，定性分析了爆炸能量的分布方向。Sanchidrián 等[7]通過單孔爆破試驗計算了巖體內炸藥爆破后的能量分布，計算結果表明，地震波能量占炸藥總能量的1%～3%，破碎能占炸藥總能量的2%～6%，動能占炸藥總能量的3%～21%。Hong 等[8]通過霍普金森壓桿試驗得出：爆炸產生的沖擊波能量撞擊炮孔壁后分散為反射能、透射能及巖體破碎能，且巖體破碎能的分配隨總入射能的增加近似線性提高。

炸藥爆炸傳遞至巖體中能量的多少與炸藥性能、巖體性質和裝藥結構有關，為提升炸藥的能量利用率，學者們對炸藥（耦合裝藥和不耦合裝藥）與礦巖的匹配進行了廣泛的研究，提出了波阻抗匹配[9]、全過程匹配[10]和能量匹配[11]等觀點。采用不耦合裝藥爆破時，耦合介質不同，爆破效果和傳至巖體能量的多少也有顯著差異。陳世海等[12]從理論上對水介質耦合裝藥爆破與炸藥耦合裝藥的破巖效能進行了討論，認為水介質耦合裝藥爆破更能提高炸藥的能量利用率；宗琦等[13]推導了水介質耦合條件下的孔壁峰值壓力和破巖范圍，認為炮孔水介質耦合裝藥比空氣介質耦合裝藥更能提高爆炸能量利用率，增強破巖能力。Jang[14]通過數值模擬和現場試驗分析了水墊層對巖體爆破的影響，發現爆炸能量與水相互作用在孔底產生了均勻連續的壓力轉換，使爆塊尺寸分布更加均勻，沒有巨石產生。顧文彬等[15]、Xia 等[16]分析了裝藥結構對能量傳遞的影響，發現爆炸能量的傳遞受到炸藥與巖石的波阻抗、不耦合裝藥系數及炮孔內耦合介質的壓縮程度影響，不同裝藥結構能量利用存在差別。但是目前的分析多停留在試驗及定性分析階段，缺乏定量化指標。

本文中將基于波動方程、率相關的巖體破壞分區模型，求解不同耦合介質爆破時爆炸能量的理論傳遞效率，并通過數值模擬分析耦合介質對爆炸能量傳遞效率的影響。

1 不耦合裝藥爆破孔壁爆炸荷載峰值計算

不耦合裝藥爆破時，炸藥爆炸產生沖擊波，沖擊波在傳播過程中先后與耦合介質及巖體發生碰撞，并在介質交界面發生透反射。在不同介質的交界面上，界面兩側應存在應力和位移連續，同時任意沖擊波均滿足質量、動量及能量守恒方程[17]：

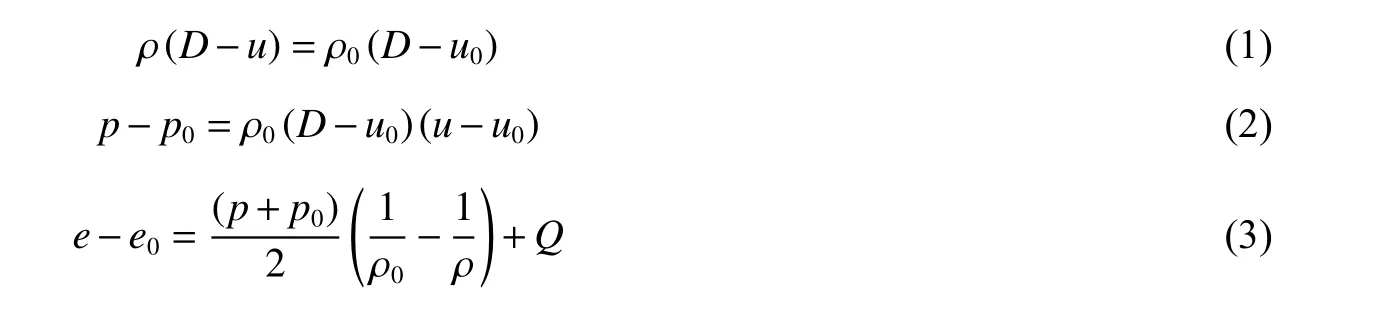
式中：下標0 表示波前參數，其余為波后參數；Q為介質的比能，若介質不釋放能量，則Q=0；p、ρ、u、D分別為沖擊波的壓力、密度、質點速度及傳播速度，e為比內能。

1.1 空氣耦合爆破

空氣耦合爆破時，炮孔壁入射壓力與爆生氣體的膨脹過程有關，當不耦合系數較小時，爆生氣體在炮孔內僅經歷等熵膨脹，此時孔壁入射壓力為[9]：

當不耦合系數較大時，爆生氣體在炮孔內經歷等熵膨脹及絕熱膨脹，此時孔壁入射壓力為[9]：

式中：pi為炮孔壁入射壓力，pw為平均爆轟壓力，pk為臨界壓力，ρe、D分別為炸藥密度及爆速，dc、db分別為裝藥直徑及炮孔直徑，k、γ 為絕熱指數。

根據爆生氣體與巖體交界面上的位移連續，可得[3]：

式中：ui為入射波孔壁質點速度，ut和ur分別為透射波及反射波孔壁質點速度。

根據波的質量和動量守恒可得任意介質中波的質點速度，即：

式中：ρi0為入射波波前密度，即空氣初始密度；ρt0為透射波波前密度，即原巖密度。

多方氣體的狀態方程為[6]：

由氣體狀態方程結合反射波守恒方程可得：

由交界面上應力連續條件可得：

取巖石的狀態方程為：

式中：A′為常數，與巖體性質有關；k′為巖石的等熵指數。

聯立式（6）～（13）可得空氣耦合裝藥孔壁透射峰值壓力。

1.2 水耦合爆破

水耦合爆破時，爆生產物首先與水發生碰撞，在水中激起沖擊波，在爆生產物與水的交界面上同樣滿足位移及應力連續條件。由瞬態爆轟的爆轟波波陣面參數基本公式可得[3]：

根據爆轟產物多方曲線狀態方程及反射波動量守恒方程可得：

將式（14）～（15）代入式（6）可得：

水的狀態方程可表示為：

式中：A′′為常數，k′′為水的等熵指數，ρw0為水密度。

聯立式（9）、（16）～（17）可得水耦合爆破水中沖擊波初始峰值壓力。

沖擊波在水中傳播伴隨著能量耗散及幾何衰減，延長藥包裝藥水中超壓隨相對距離的衰減關系為[18]：

式中：A1為水中沖擊波初始峰值壓力，為相對距離，=r/rc，其中r為距炮孔中心距離，rc為藥卷半徑。

由式（18）可得水巖界面入射壓力，水耦合爆破孔壁透射峰值壓力推導過程與空氣耦合裝藥相近，聯立式（6）、（12）～（13）、（17）可得水耦合爆破孔壁透射峰值壓力。

2 基于率相關的巖體爆破破壞范圍計算

在爆炸荷載作用下，炮孔周圍巖體發生破壞，炮孔近區巖體由近及遠分為粉碎區、裂隙區及彈性振動區,但這種巖體破壞分區模型忽略了裂隙區的環向承載力，與實際分布存在較大偏差。冷振東等[19]根據現場試驗觀察提出，在粉碎區及裂隙區間，存在以受壓及剪切破壞為主的破碎區，破碎區內沖擊波衰減較緩。巖體在爆炸荷載作用下處于強動力響應狀態，炮孔近區巖體應變率為：

式中：urb為孔壁峰值質點速度；rb為炮孔半徑；α 為壓力衰減指數，α=2±μ/(1?μ)，在不同破壞區域α 的取值不同。

巖體中任意一點的有效應力為[20]：

根據有效應力強度準則，當σi滿足下式，巖體將會發生破壞：

式中：κ為靜單軸抗壓強度縮小系數，σcd為巖石靜態抗壓強度，σtd為靜態抗拉強度，ε ˙c0、ε˙t0分別為抗壓強度及抗拉強度臨界應變率。

聯立式（19）～（21），可得不耦合裝藥爆破巖體破壞范圍，粉碎區范圍：

破碎區范圍：

裂隙區范圍：

式中：σr1、ur1為粉碎區邊界位置質點應力及振動速度，ε˙θ=ur1α3(r3/r1)?(α3+1)/r1；α1、α2、α3分別為粉碎區、破碎區及裂隙區應力波衰減指數。

3 不耦合裝藥爆破傳遞入巖體內能量計算

3.1 沖擊波能量

3.1.1沖擊波爆腔膨脹

在爆炸沖擊荷載作用下，孔壁巖石將會壓縮，爆腔發生膨脹。爆腔膨脹在巖石壓碎過程中持續存在，在破碎區邊緣，沖擊波引起的爆腔膨脹同步結束，粉碎區及破碎區均消耗了大量沖擊波能量。沖擊波擴脹爆腔的過程中，擴脹范圍內巖體質量守恒，因此有：

式中：rk為沖擊波擴脹后爆腔的半徑，r2為巖體破碎區范圍，ρm為原巖密度，ρ為沖擊波波陣面上的巖石瞬態密度。

爆腔擴脹過程中，其波陣面后巖石密度變化很小，因此沖擊波陣面上巖石瞬態密度ρ 可用壓縮后孔壁處巖石密度ρr代替，根據波陣面上巖石質量守恒以及巖體Hugoniot 方程可得：

式中：a、b為與巖性相關的參數。

聯立式（25）～（26）可得，沖擊波爆腔擴脹半徑為：

由此可得沖擊波消耗在巖體爆腔擴脹上的能量為：

3.1.2沖擊波裂隙擴張

沖擊波在巖體內逐漸衰減，在破碎區邊緣基本衰減為應力波，此時徑向應力已經小于巖體抗壓強度，但環向應力仍大于巖體抗拉強度，會引起巖體開裂。巖體中r處的應力波切向應力為：

此時裂隙長度為a，若σθ>[σtd]，裂隙將進一步擴展，假定裂隙擴展到a+δa時，切向應力衰減到抗拉強度，裂隙停止擴展；此時裂隙在切向應力作用下產生了切向位移，切向力對巖體做功，在此過程中切向力做功近似為：

由斷裂力學可得[21]：

式中：f=(3?4μ)，k1、k2為長度不同的裂隙端部的應力強度因子，為簡化計算可近似認為裂隙擴展過程中強度因子保持不變，Em為巖石彈性模量。

聯立式（30）～（32）可得裂隙擴展過程中切向應力所做的功為：

式中：n為徑向主裂隙條數，根據相關試驗文獻，n=4～12。

3.1.3應力波引起的彈性變形

隨著應力波的進一步衰減，裂隙區外應力波不再造成巖體破壞，僅引起彈性振動，柱狀坐標系下單位體積巖體發生彈性變形需要的能量為[22]：

由變形區r→∞得到，應力波引起巖石彈性變形所做的功為：

3.2 準靜態爆生氣體能量

3.2.1準靜態荷載擴腔

在沖擊荷載作用之后，爆生氣體膨脹壓縮耦合介質，以準靜態荷載的形式作用在孔壁上，爆腔進一步擴大，當爆腔內準靜態壓力p等于圍巖壓力ps時，準靜態爆腔擴脹結束。不考慮大氣壓力及圍巖自重影響，巖體中圍巖壓力近似為三軸應力狀態下巖石的屈服強度σs，其中σs=(ρmc2p/σcd)1/4σcd，其中cp為巖體縱波波速。

考慮到爆生氣體在空氣與水中的膨脹差異，分別對空氣耦合及水耦合爆破準靜態擴腔過程進行分析。

（1）空氣耦合裝藥

空氣耦合爆破時，爆生氣體的膨脹過程與距起爆中心的距離有關，根據式（4）～（5）可得炮孔內任一點爆生氣體的膨脹壓力為：

（2）水耦合裝藥

沖擊波擴腔結束后，爆生氣體膨脹壓縮水至充滿爆腔，設此時膨脹壓縮過程結束后水的徑向壓縮量為δ，由水的質量守恒可得壓縮后水的密度為：

根據流體力學理論，水在壓縮過程中滿足：

聯立式（36）、（38）～（39）可得沖擊波擴腔結束后爆生氣體半徑。

準靜態爆生氣體擴腔完成后，由準靜態爆腔擴脹條件可得炮孔內壓力平衡方程：

式中：ph為不耦合介質水中壓力。

聯立式（36）～（40）可得準靜態爆腔擴張結束后爆生氣體半徑，此過程爆生氣體膨脹準靜態做功為：

3.2.2準靜態荷載作用下裂紋擴展

研究表明[23]，巖體在應力波作用下產生初始裂隙，隨后裂隙在爆生氣體準靜態荷載作用下進一步擴展。考慮到裂隙長度通常遠大于炮孔尺寸，因此可將炮孔尺寸近似為裂隙長度的一部分，此時裂紋尖端的應力強度因子為[24]：

式中：L(t)為準靜態擴展裂紋長度，N為裂紋尖端初始損傷，p(x,t)為裂隙內準靜態荷載分布，σ 為遠場應力。

當滿足下式時裂紋擴展終止：

假定最終裂紋長度為L，對應炮孔內壓力為p，聯立式（36）、（42）～（43）可求得考慮初始損傷情況下最終裂紋長度L，進而求得爆生氣體準靜態作用裂紋擴展做功為：

3.3 爆炸傳遞入巖體總能量

炸藥爆炸傳遞入巖體內的能量最終消耗于粉碎區、破碎區、裂隙區及彈性振動區，因此各部分能量總和即為爆炸傳遞入巖體內能量，它們與炸藥能量的比值即為不耦合裝藥爆破爆炸能量傳遞效率，即：

式中：E為單位長度炸藥的總能量。

以乳化炸藥、花崗巖為例，計算典型裝藥結構的不同耦合介質爆破時爆炸能量傳遞的效率。乳化炸藥（ρe=1 300 kg/m3，D=4 000 m/s）的體積爆熱為4.192 GJ/m3，花崗巖力學參數如表1所示[25]。

表1 花崗巖力學參數Table 1 Mechanical parametersof granite

不同耦合介質爆炸能量傳遞效率計算結果如表2所示。根據計算結果可知，水介質相較于空氣介質具有更好的能量傳遞效果。同時，相較于空氣，水的流動黏度大、壓縮性低、沖擊波衰減緩慢，造成的粉碎區范圍大于空氣耦合，耗散于粉碎區的能量更多，計算結果與相關試驗結論接近。

表2 不同耦合介質爆炸能量傳遞效率Table 2 Energy transfer efficiency of blasting explosion with different coupling medium

上述研究建立在爆炸荷載垂直作用孔壁的假定基礎上，未能完全真實考慮爆炸荷載斜入射以及反射帶來的影響，同時爆炸荷載在炮孔耦合介質中的衰減也較難得出理論解，需要采用部分經驗公式，這些假定及經驗公式為理論上定量分析不同耦合介質爆破的具體能量差異帶來困難，可能造成分析結果出現一定誤差。下面結合高精度數值模擬方法，分析不同耦合介質爆破時爆炸能量傳遞效率的差異及其影響因素。

4 不同耦合介質爆破爆炸能量傳遞效率數值模擬

4.1 計算模型及參數

為進一步研究不同耦合介質爆破時爆炸能量傳遞效率的差異以及爆破介質、不耦合系數及炸藥種類對能量傳遞效率差異的影響，基于實際開挖過程中巖體種類的分布、常用爆破參數及工業炸藥類型，選擇粉砂巖、石灰巖及花崗巖3類性質差異明顯的巖體，分別代表軟、硬及堅硬類巖體介質，同時選用6種常用不耦合裝藥系數，以及乳化炸藥和多孔粒狀銨油炸藥2種典型工業炸藥開展相關研究。

數值計算采用非線性動力有限元軟件LSDYNA，計算模型如圖1所示，為1/4炮孔模型，尺寸為1.5 m×1.5 m×3 m，為確保能較準確地模擬出真實的爆炸效應，將計算模型中炸藥和耦合介質單元的網格尺寸控制在2 mm 左右，鄰近巖石單元尺寸也與炸藥/耦合介質單元近似相同，模型網格數量約38萬，不同工況時保證模型尺寸及網格劃分基本一致，計算時間步與模型最小網格匹配；模型邊界包括無反射邊界、對稱邊界及自由邊界；采用流固耦合算法模擬爆炸荷載的沖擊作用。

圖1 數值模擬計算模型Fig.1 Numerical simulation model

炸藥采用JWL 狀態方程進行模擬，其爆炸過程中的壓力和內能及相對體積之間的關系為：

式中：p為爆轟壓力，V為爆轟產物的相對體積，其余為方程常數。計算炸藥相關參數取值見表3。

表3 計算炸藥參數Table 3 Table of chargeparameters

巖體材料采用雙線性隨動硬化塑性模型，該模型可以較好地考慮巖體破壞過程中的應變硬化，應變率敏感性以及毀傷失效等特征，與理論分析中基于應變率的巖體破壞分區模型相對應，數值模擬中采用的巖石力學參數如表4所示，與理論計算參數對應，均取自巖石力學參數手冊推薦范圍[25]。

表4 計算巖體力學參數表Table4 Table of mechanical parameters of rock mass used in the simulations

LS-DYNA 中空氣采用mat_null 材料模型結合*EOS_Linear_Polynomial狀態方程描述；水采用mat_null材料模型結合*EOS_Grüneisen 狀態方程描述，相關參數取值見文獻[19]。

4.2 計算結果

圖2中給出了部分典型工況下的爆炸能量時程曲線。由圖2可知，相同裝藥結構下，相較于空氣介質，水介質具有更好的傳能效果，且爆炸能量增長速率顯著快于空氣介質，這與水的壓縮性顯著低于空氣、黏滯度大于空氣有關，與耦合介質的物理性質差異相匹配；隨著時間的推移，爆炸傳至巖體內的能量趨于穩定，水耦合爆炸能量傳遞效率顯著高于空氣耦合裝藥，數值模擬結果與前述理論分析結果基本一致。

圖2 典型工況下爆炸能量時程曲線Fig.2 Time history curve of explosion energy under typical working conditions

不同工況下不同耦合介質爆破時爆炸能量傳遞效率比值如圖3所示。

圖3 不同裝藥結構下不同耦合介質能量傳遞效率比值Fig.3 The ratio of energy transfer efficiency for different coupling medium under different chargestructures

由計算結果可知，不同耦合介質間能量傳遞效率的差值并非定值，受到爆破介質、炸藥性質以及不耦合裝藥系數的影響。在相同裝藥條件下，花崗巖水耦合爆破比空氣耦合爆破時爆炸能量傳遞效率的提升更加明顯，石灰巖、粉砂巖次之，即巖體強度越高能量傳遞效率差別越大；炸藥性質對不同耦合介質爆炸能量傳遞效率的差值也存在一定的影響，采用乳化炸藥爆破時不同耦合介質能量傳遞效率差異比采用銨油炸藥爆破小；當采用同種炸藥爆破相同巖體介質時，能量傳遞效率的差異隨不耦合系數的增大逐漸增大，在不耦合系數較小時，不同耦合介質能量傳遞的效率基本相同，極端情況接近耦合裝藥情況下，兩者能量傳遞效率基本相當；當不耦合系數較大時，水耦合爆破比空氣耦合爆破具有更好的能量傳遞效果；以乳化炸藥在粉砂巖中起爆為例，不耦合系數由1.28增至3.44時，水耦合爆破傳遞入周圍巖體的能量由空氣耦合爆破的1.45倍增至6.52 倍。

5 結 論

通過理論及數值模擬分析，研究了不同耦合介質爆破時爆炸能量傳遞的效率及其影響因素，得到以下主要結論：

（1）基于波動方程及界面連續條件，求解了不耦合裝藥爆破孔壁爆炸荷載峰值，進而得到了基于率相關的巖體破壞區范圍，并進行了分區能量計算，得到不同耦合介質爆破時爆炸能量的理論傳遞效率；

（2）裝藥結構相同時，水耦合爆破比空氣耦合爆破減少了爆炸荷載在耦合介質中的衰減，爆炸荷載峰值壓力高、作用時間長，提高了爆炸能量傳遞的效率；

（3）不同耦合介質爆破時爆炸能量傳遞效率的差值并非定值，受到爆破介質、炸藥性質以及不耦合裝藥系數的影響，相同裝藥條件下，硬巖（花崗巖、石灰巖）比軟巖（粉砂巖）不同耦合介質爆破時能量傳遞效率的差別更大；

（4）爆破工況相同時，不同耦合介質爆破時爆炸能量傳遞效率的差異隨不耦合系數的增大逐漸增大，以乳化炸藥在粉砂巖中起爆為例，不耦合系數由1.28增至3.44時，水耦合爆破傳遞入周圍巖體的能量由空氣耦合爆破的1.45 倍增至6.52倍。