哈夫曼樹在排序算法中的案例教學研究

吐爾地·托合提，崔青，劉淑嫻

（新疆大學信息科學與工程學院，烏魯木齊 830046）

0 引言

哈夫曼樹（Huffman Tree），又被稱為最優二叉樹，是一種帶權路徑長度最小的二叉樹，其應用也很廣泛，如基于哈夫曼樹的編碼[1]、壓縮[2-3]、加密[4-5]、數據采樣[6]等。在教學中，一般我們重點講解帶權路徑長度的概念、哈夫曼樹的性質、哈夫曼樹的構造，以及哈夫曼編碼[8]。其實，哈夫曼樹也可以用來對于數據元素序列進行排序。

從哈夫曼樹的性質可知，權重越大的葉子結點越靠近根結點，而權重越小的葉子結點離根結點越遠。因此，將待排序序列中的每一個元素看成一個葉子結點，將元素關鍵碼看成其權重（關鍵碼為整形情況下），構造一棵哈夫曼樹，然后層序遍歷并依次輸出葉子結點，就能得到基本有序（降序）序列。如果，在哈夫曼樹的構造、遍歷和輸出過程中增設一些約束，那么也完全可以做到對數據元素的降序或升序排序。

本文在數據結構教學中，針對內部排序提出一個教學案例，在排序方法中引入哈夫曼樹、二叉樹的遍歷、棧和隊列等綜合內容，通過講解一些啟發思路的知識點，一方面加深了學生對于哈夫曼樹的性質、構造方法、二叉樹遍歷算法，以及哈夫曼樹、棧和隊列應用的理解和掌握，另一方面引導學生要認識到解決問題有多種方案可選，鼓勵學生從知識中體會和掌握算法設計的思維方式和技巧，這有助于使學生分析問題和解決問題的能力得到提升。

1 基于哈夫曼樹的排序算法思路

在待排序序列中數據元素關鍵碼為整形（int 形）情況下，我們可以將每一個數據元素看成一個葉子結點，將數據元素關鍵碼看成其權重構造一棵哈夫曼樹。設待排序數據元素關鍵字序列為{5，9，15，30，18，27，10，13}，在構造哈夫曼樹的過程中我們給一個約束：將權重大的結點作為左孩子，將權重小的結點作為右孩子，然后按照哈夫曼樹的構造方法就能生成得到如圖1 所示的一棵哈夫曼樹。

我們仔細觀察圖1 哈夫曼樹中葉子結點（待排序元素結點）分布，第一層為根，從第二層開始，發現處在第i 層上元素關鍵字均小于第i-1 層元素關鍵字，而均大于第i+1 層元素關鍵字，最底層上的元素關鍵字是最小。再觀察同一個層上的元素關鍵字大小，從左到右，關鍵字大小依次變小。因此，我們對此哈夫曼樹進行層序遍歷并輸出葉子結點關鍵字，就能得到一個關鍵字有序（降序）序列{30，27，18，15，13，10，9，5}，這樣就可以做到降序排序。如果，需要進行升序排序，我們可以借助一個棧來暫存層序遍歷輸出序列，最后依次出棧就能得到升序排序結果。

圖1 由待排序元素關鍵字構建的哈夫曼樹

2 基于哈夫曼樹的排序算法實現

根據以上分析，我們可以設計一套用來排序的哈夫曼樹構造算法和排序算法。為了簡單討論，以下假設關鍵碼為整形，而且只考慮關鍵碼，暫不考慮數據元素其他數據項。

構造哈夫曼樹時，常用一個結構數組（如Huff_Nodes）來存儲哈夫曼樹中每一個結點的信息。我們從二叉樹的性質可知，由n 個葉子結點構建的哈夫曼樹中總共有2n-1 個結點，所以結構數組Huff_Nodes 大小可設置為2n-1，其元素結構可定義如圖2 所示形式。

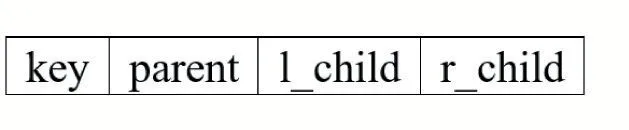
圖2 結構數組元素結構形式

其中，key 域是用來保存待排序數據元素關鍵字（傳統算法中的結點權值weight），l_child 域和r_child域是分別用來保存該結點的左孩子和右孩子結點在數組中的下標（序號），算法中我們通過下標在結點之間建立聯系。parent 域保存當前結點在哈夫曼樹中的雙親結點在數組中的序號，其初始值為-1。

2.1 哈夫曼樹的構造算法

開始構造哈夫曼樹之前，首先把n 個關鍵字形成的n 個葉子結點存放在結構數組Huff_Nodes 的前n 個分量中，然后根據哈夫曼樹構造基本思想和本文給出的約束條件，不斷將兩個根結點權重最小的子樹合并為一個較大的子樹，并把被生成的新子樹的根結點依次按順序存放到Huff_Nodes 數組前n 個分量后面。具體實現算法描述如下：

算法初始化Huff_Nodes 數組并依次向數組填寫新生成的子樹信息（子樹根結點關鍵字、根結點左右孩子在數組中的序號），同時，還不斷修改與已有子樹之間的關聯信息。當算法結束時，用來存儲圖2 所示哈夫曼樹的結構數組Huff_Nodes 的最終狀態如圖3 所示。

圖3 數組Huff_Nodes的最終狀態

2.2 基于哈夫曼樹層序遍歷的排序算法

已構建好的哈夫曼樹的根結點在數組Huff_Nodes的最后一個單元中，我們從根結點出發進行層序遍歷（從上到下，從左到右），并把那些葉子結點依次暫存到一個棧中，等遍歷結束就出棧所有元素，此時的出棧序列就是一個升序排序序列。如果要進行降序排序，那就不需要經過棧來改變次序，在遍歷中直接輸出葉子結點即可。升序排序具體實現算法描述如下：

3 結語

排序是數據結構課程最后一章內容，一般我們主要講解各種典型內部排序算法思路，分析其性能和優缺點，然后要求學生通過運行、調試排序程序去掌握多種排序算法，但很少有拓展內容。本文針對內部排序設計一個教學案例，將棧、隊列、哈夫曼樹等重要內容綜合應用到排序方法中。其目的不僅僅是提出一個排序算法，而更重要的是鼓勵學生敢于創新，引導學生從知識中體會和掌握算法設計的思維方式和技巧，從而培養學生創造性思維能力及解決實際問題的能力。