基于計算智能的地鐵隧道施工進度 - 成本優化

杜 鍍，王肖輝

(河南建筑職業技術學院 a. 工程管理系； b. 土木工程系， 河南 鄭州 450064)

中國的城市化進程越來越快，為了滿足城市居民出行需求，城市地鐵項目建設也在逐步進入正軌，現國內一些城市正在開始或完善地鐵項目建設。地鐵隧道施工一般采用兩種或兩種以上的開挖方法(明挖法，新奧法，盾構法等)，整個施工的距離較長，施工強度大，施工工序繁多[1]，因此施工周期比較長，當然整個施工項目投資也比較大。如何在地鐵隧道項目施工過程中對進度和成本進行有效管理是非常關鍵的。

進度 - 成本優化方法中屬于網絡計劃方法的PERT(Program Evaluation and Review Technique)和CPM(Critical Path Method)是最早被美國海軍采用的方法[2]。為實現進度和成本的優化，葉天翔[3]采用了邊際成本法進行進度和成本的優化。該方法通過不斷壓縮關鍵工作，反復人工操作計算實現。汪萬竹[4]針對工程項目進度 - 成本優化問題，采用CPM法建立了進度 - 成本的線性規劃模型，基于該模型同時引入極限成本，通過求解線性規劃模型的方法實現進度 - 成本優化。李遷等[5]在考慮空間干涉的作用下，建立了該情況下工程調度進度和成本優化的數學模型，最后通過元啟發式算法進行優化。在保證工程質量的前提下，宋寶軍[6]研究了進度 - 成本優化問題，利用企業實踐數據，創建了進度 - 成本優化的數學模型，然后運用遺傳算法實現進度成本的尋優。分析以上學者所采用的方法可知，通過人工操作計算來反復調整實現進度 - 成本優化過程是非常復雜的，隨著工程項目越來越復雜，這種方法將會很難執行；通過相關數據來首先建立進度 - 成本的數學模型，然后再基于相關算法實現優化對于小型的工程比較適用，但是當工程項目比較復雜時，進度和成本之間的關系將很難用數學公式準確表達，有的甚至無法表達相互關系。因此，對于復雜項目下的進度 - 成本優化方法需要進一步研究。

本文基于計算智能技術的發展，將計算智能技術中的方法相結合，用非線性處理能力較好的神經網絡[7～9]來表達約束系統，再采用智能優化算法進行尋優，對于復雜的涉及工序較多的工程，就可以避免采用復雜或不準確的數學公式。基于這種思路，本文提出運用一種基于遺傳神經網絡和免疫粒子群算法的組合方法來解決復雜工序下的進度 - 成本優化問題。為驗證該組合方法的性能，選取一般可以建立準確數學公式的案例進行驗證，分別采用基于數學模型的單純形法和該組合方法來求解進度 - 成本優化問題。從而以數學模型方法所求的準確結果為參照，若相對誤差較小(控制在10%以內)，則說明該組合方法能夠較為準確地解決進度 - 成本優化這一類問題，從而可以將其應用于大型城市地鐵隧道施工進度 - 成本優化問題中。

1 計算智能技術

計算智能屬于智能的范疇，是由美國學者James首次提出，計算智能主要是從生物進化的角度學習和模擬智能，也被稱之為“軟計算”。計算智能技術方法一方面在各自獨立地進行研究和發展，另一方面計算智能所包含的各種方法之間以及計算智能技術和其他方法之間也在互相融合發展，其中，各種技術或方法的融合發展往往可以解決單一方法難以解決的問題[10]。遺傳神經網絡和免疫粒子群算法均屬于該領域。

1.1 遺傳神經網絡

BP(Back Propagation)神經網絡屬于一種誤差逆向傳播的多層前饋神經網絡，該網絡采用梯度下降法對層間的權值和節點的閾值進行修正，通過網絡的不斷訓練，即對權值和閾值的不斷修正，來實現實際輸出和期望輸出的均方差達到最小。

BP神經網絡的應用比較多，但在發展應用的同時也存在一些缺陷，其中，BP神經網絡很容易陷入到局部極值，從而導致訓練失敗。因此，本文為了降低BP神經網絡陷入局部極值的可能性，采用遺傳算法對BP神經網絡的初始權值和閾值進行優化[11]，從而提高BP神經網絡的訓練效果，更好地對進度和成本之間的關系進行擬合。

1.2 免疫粒子群算法

粒子群算法屬于計算智能中的群智能算法，該算法來源于對鳥群覓食過程的模擬，通過個體極值和群體極值不斷的去搜索最優值。從算法結構來說，該算法比較簡單，運行速度較快，因此，被廣泛采用。與此同時，該算法中粒子也因為自身缺乏調節機制，導致在迭代后期粒子的多樣性較差，這便很容易導致在迭代后期陷入局部極值。所以，為了更準確地進行進度 - 成本優化，本文將免疫自我調節機制用于粒子群算法的迭代[12]，提高該算法在迭代過程中的粒子多樣性，從而能夠更準確地獲取到全局最優值。

基于遺傳神經網絡和免疫粒子群算法的組合方法解決一般約束系統優化問題的流程如圖1所示。

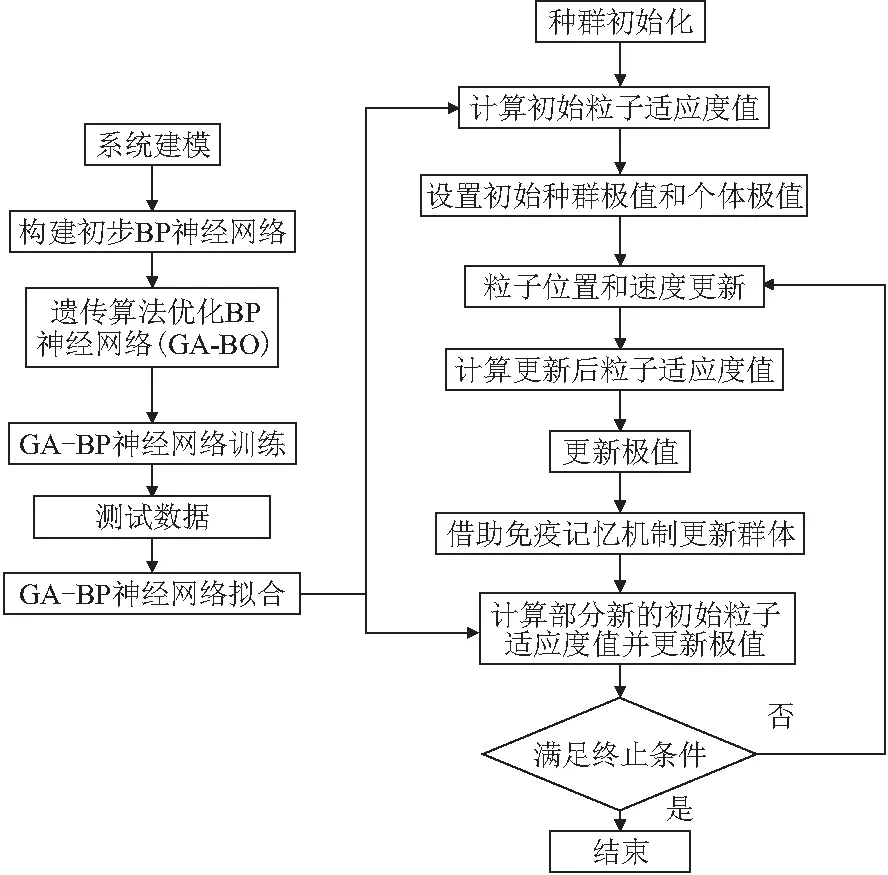
圖1 基于遺傳神經網絡和免疫粒子群算法的組合方法解決一般約束系統優化問題的流程

2 基于遺傳神經網絡和免疫粒子群算法的進度 - 成本優化模型

2.1 進度 - 成本優化

在工程項目施工前，一般需要編制工程項目進度計劃，其中進度計劃都由許多必要的工序組成，這些工序在實際施工時將消耗相應的資源，包括人力、材料、機械等。其中評估進度計劃編制的科學性和可行性的重要經濟指標就是成本，因此，需要對初次編制的進度計劃不斷的優化。進度 - 成本優化[13]在不同條件下的優化結果是不同的，本文考慮的是在資源充分和關鍵線路保持不變的條件下，實現對進度 - 成本的優化，從而在滿足工期條件的情況下，費用最低。

2.2 進度 - 成本優化模型構建

利用整個工程所有工序的直接壓縮費率來確定出一定樣本量的各工序不同壓縮時間組合與對應的直接壓縮費用數據，用這些樣本訓練遺傳神經網絡，從而建立不同壓縮時間組合與直接壓縮費用關系的神經網絡模型，再運用免疫粒子群算法并結合工程施工工期、各工序時間和關鍵線路不變的要求進行尋優。具體步驟如下：

Step1：基于進度成本相關數據和MATLAB編程，獲取各工序壓縮時間組合與對應直接壓縮費用的數據樣本。

Step2：建立初始BP神經網絡模型，同時使用遺傳算法來實現對BP神經網絡權值和閾值進行優化。

Step3：運用各工序壓縮時間組合與對應直接壓縮費用的訓練樣本對優化后遺傳神經 (GA-BP，Genetic Algorithm and Back Propagation) 網絡進行訓練，并用測試樣本檢驗網絡擬合和泛化效果，反復訓練與檢驗，保存可行的網絡(net)。

Step4：設置免疫粒子群算法參數，并對免疫粒子群算法中各粒子位置(各工序壓縮時間的組合)進行初始化，以及初始化粒子各方向速度(各工序壓縮時間的變化量)。

Step5：采用上面保存的網絡(net)進行初始各粒子適應度值計算。粒子i適應度值fitness(i)計算采用的核心代碼為：

w(i)=sim (net, input (i));

fitness(i)=mapminmax(‘reverse’,w(i),outputps)

其中：input (i)為粒子i的位置經過歸一化后的向量；w(i)為未反歸一化的適應度值。

Step6：進行個體極值設置，同時，個體極值中fitness數值最小的設為群體極值。

Step7：運用式(1)(2)進行粒子速度和位置的更新。

vik=ωvik+c1r1(pik-xik)+c2r2(pgk-xik)

(1)

xik=x′ik+vik

(2)

式中：ω為權值；c1，c2為學習因子；r1，r2為(0,1)之間的隨機數；vik為第i個粒子第k個方向的速度；pik為第i個粒子第k個方向上的位置；pgk為群體極值在第k個方向的位置；xik為第i個粒子的第k個方向的位置。

Step8：檢驗更新后的各粒子位置(各工序壓縮時間的組合)是否符合壓縮條件，以及粒子速度是否在要求范圍之內。

Step9：對當前粒子進行適應度值的計算，同時再更新群體極值和個體極值。

Step10：對計算出的各粒子fitness值進行從小到大排序，保留fitness值較低的，且保留數量為種群規模的一半，舍棄另外粒子。然后再重新初始化舍棄的粒子，并計算對應的適應度值，與保留下來的粒子構成下一代粒子種群。群體極值和新初始化的粒子個體極值更新。

Step11：循環Step7～Step10到迭代次數結束。

3 算例分析

運用可建立準確數學公式的文獻[14]項目進度 - 成本優化問題來驗證組合方法的可行性。各工序工期、方差、壓縮范圍、壓縮費率如表1所示。

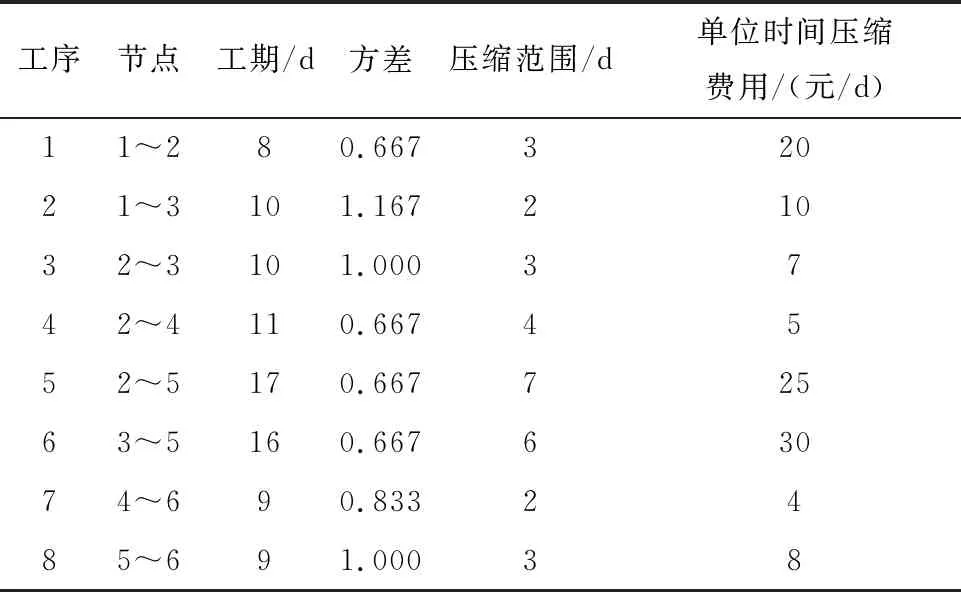
表1 工序數據

各工序壓縮時間變量見表2，分別采用基于遺傳神經網絡和免疫粒子群算法的組合方法和基于數學公式的單純形法求解。

表2 工序壓縮時間表示符號

3.1 基于遺傳神經網絡和免疫粒子群算法的尋優過程

MATLAB中的randint()函數可以在一定取值范圍內以均勻分布方式隨機取值，因此，本文根據以上表格數據和閉合圈原理[14]，利用randint()函數獲取訓練樣本和測試樣本的取值。

根據每個工序的時間壓縮范圍設置randint( )函數取值范圍，從而獲得符合壓縮時間要求的每個工序壓縮時間，再通過所有工序單位時間壓縮費用得出相應的增加成本，最終獲得多組符合要求的所有工序壓縮時間的組合和對應壓縮費用，從而作為神經網絡輸入和輸出樣本。本文取170組訓練樣本和8組測試樣本[12]。

(1)擬合壓縮時間和直接壓縮費用關系的神經網絡訓練和測試

因該算例中的變量為8個(x1～x8)，目標函數為直接壓縮費用C，所以輸入層節點數(inputnum)為8個，輸出層節點數(outputnum)為1個[15]。通過不同隱含層節點數(hiddennum)的BP神經網絡訓練后，比較最終擬合效果，從而確定隱含層節點的數目[16]，經過試驗后，隱含層節點數確定為15，訓練迭代次數取值為1000，學習效率取值為0.1，目標誤差取值為0.01。建立初步BP神經網絡的代碼如下：

net=newff(inputn,outputn,hiddennum)

遺傳算法參數設置[17～19]：迭代次數取值為20，種群規模取值為20，交叉概率取值為0.4，變異概率取值為0.2。

運用rands()函數初始化遺傳算法種群中各染色體，然后通過選擇、交叉和變異過程反復進行染色體更新。最后把最優染色體x中的對應基因值賦給神經網絡各個權值和閾值，其核心代碼為：

w1=x(1:inputnum*hiddennum);

B1=x(inputnum*hiddennum+1:inputnum*hiddennum+hiddennum);

w2=x(inputnum*hiddennum+hiddennum+1:inputnum*hiddennum+hiddennum+hiddennum*outputnum);

B2=x(inputnum*hiddennum+hiddennum+hiddennum*outputnum+1:inputnum*hiddennum+hiddennum+hiddennum*outputnum+outputnum);

net.iw{1,1}=reshape(w1,hiddennum,inputnum;

net.lw{2,1}=reshape(w2,outputnum,hiddennum);

net.b{1}=reshape(B1,hiddennum,1);

net.b{2}=reshape(B2,outputnum,1)

經過優化、訓練、和測試，最終訓練好的神經網絡測試結果如表3所示，保存擬合好的神經網絡(netBp)。

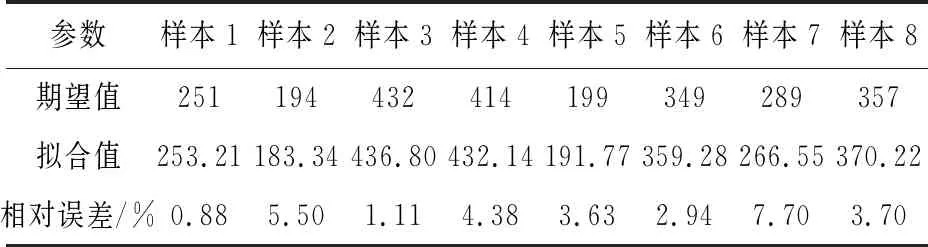
表3 測試結果

(2)基于訓練得到的網絡模型(netBp)和免疫粒子群算法進行尋優

免疫粒子群算法參數設置[20,21]：群體迭代次數取值為100，種群規模取值為50，學習因子c1，c2取值為2，粒子速度控制在[-1 1]。

基于進度成本數據和閉合圈原理，初始化各粒子位置x(i)，同時初始化粒子速度v(i)。通過訓練好的神經網絡得到初始粒子的適應度值，粒子i的適應度值fitness(i)計算如下：

w(i)=sim (netBp, x_g(i));

fitness(i)=mapminmax(‘reverse’,w(i),outputps)

其中：x_g(i)為x(i)歸一化后的位置向量。

進入迭代，根據式(1)(2)反復進行粒子速度和位置更新、群體極值和個體極值更新、以及利用免疫淘汰機制更新粒子群體等過程，直到迭代結束。

(3)結果

迭代過程如圖2所示，最終得出的最優粒子的適應度值fitnesszbest=137.52，最優粒子的位置zbest=(3,0,3,0,0,1,0,3)。所以進度 - 成本經過優化的各工序壓縮時間為：x1=3，x2=0，x3=3，x4=0，x5=0，x6=1，x7=0，x8=3，相應的壓縮費用為：137.52元。

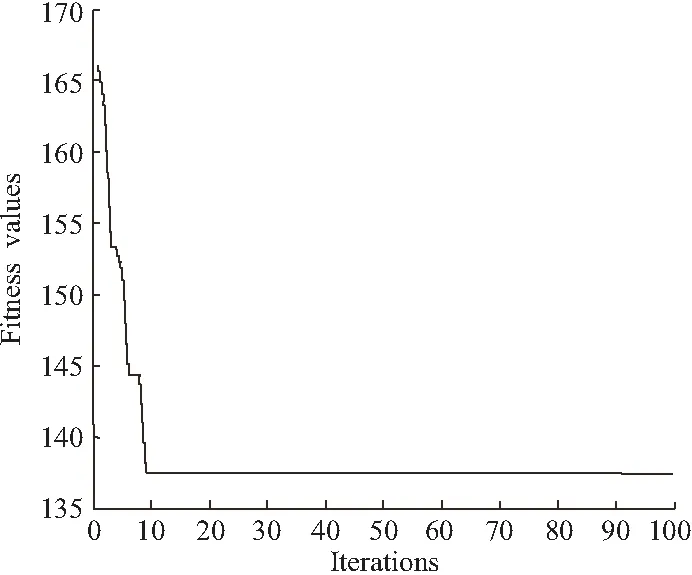
圖2 迭代過程

3.2 基于單純形法求解進度 - 成本優化問題

根據進度、成本數據和閉合圈原理，建立線性規劃數學模型如下：

minC=20x1+10x2+7x3+5x4+25x5+

30x6+4x7+8x8

首先，進行模型標準化，在約束條件中添加松弛變量x9～x20和人工變量x21，令Z=-C，則標準形式如下：

由約束系數矩陣可知，P9～P19，P21組成一個基，將所有非基變量的值設為零，即得到基可行解為x=(0, 0, 0, 0, 0, 0, 0, 0, 6.8, 7.2, 17.1, 3, 2, 3, 4, 7, 6, 2, 3, 0, 10)，據此列出初始單純形表，并根據式(3)計算初始單純形表檢驗數，初始單純形表如表4所示。

(3)

式中：aij為系數矩陣中第i行第j列的數；m為基變量的總數；cj為目標函數中變量xj前的系數。

表4 初始單純形

根據表4可知，檢驗數有大于零的，所以此時的基可行解不是最優解，其中最大的是M-7(M表示足夠大的數)，因此x3確定為換入基。用b列數字除以x3列同行數字(分母小于等于零的舍棄)，取最小值對應的基變量作為換出基，經過計算可知x14為換出基，x3列和x14行相交的數字1為主元素，加上“[ ]”符號。用x3替換基變量中x14，并列出對應的新單純形表，基于Matlab編程實現新單純形表中數據的換算。同時進行新單純形表檢驗數計算，從而檢驗基可行解是否為最優解。重復進行基變量替換、更新單純形表以及驗證檢驗數是否小于等于零，最終獲得最優解。通過操作計算，后續依次替換為：x8替換x19，x1替換x12，x6替換x21。最終的單純形表如表5所示。

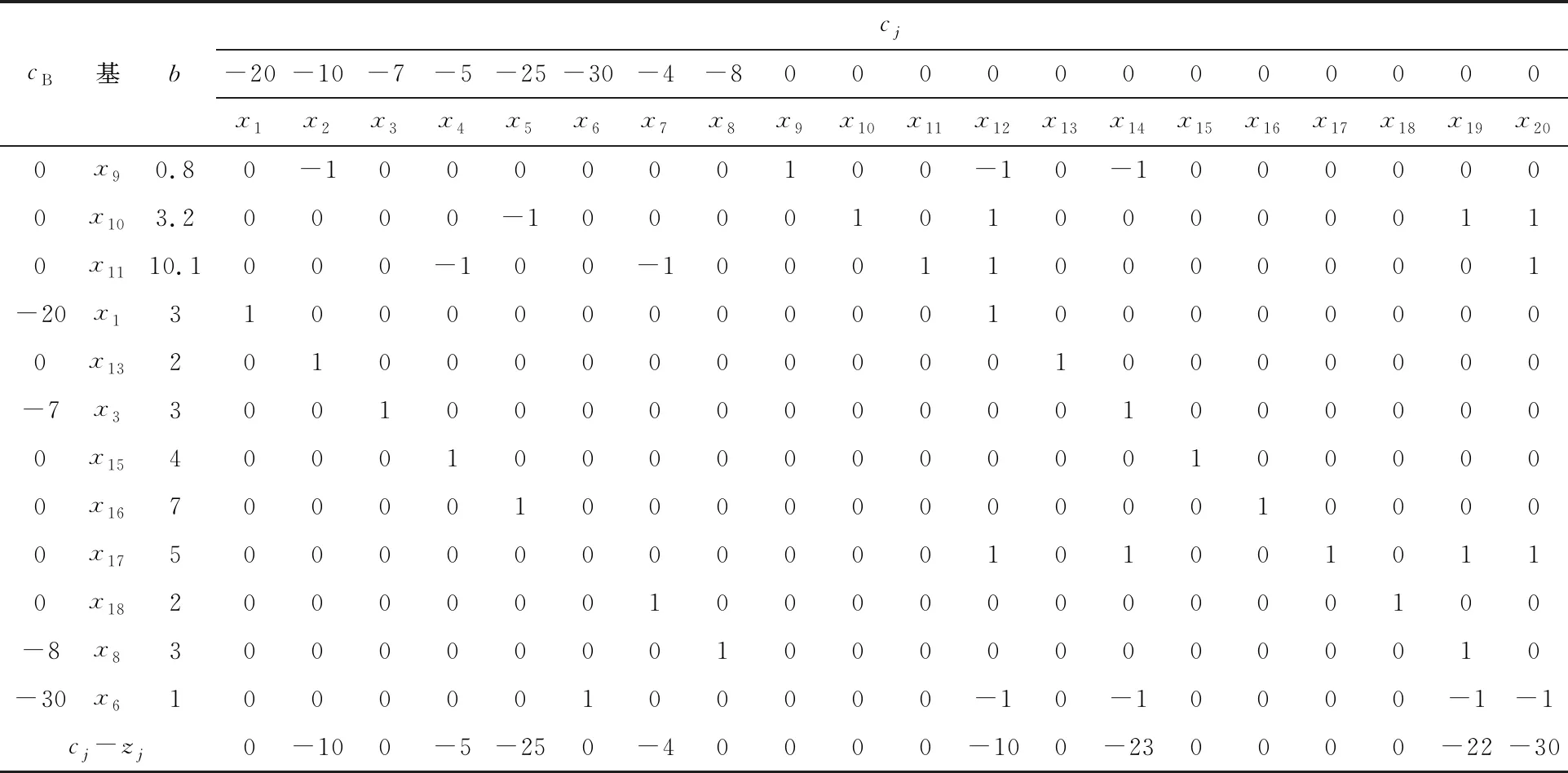
表5 最終單純形

根據表5，所有的檢驗數均不大于零，因此，對應的基可行解就是最優解，最優解為x1=3，x2=0，x3=3，x4=0，x5=0，x6=1，x7=0，x8=3，x9=0.8，x10=3.2，x11=10.1，x12=0，x13=2，x14=0，x15=4，x16=7，x17=5，x18=2，x19=0，x20=0，x21=0，帶入目標函數為Z=-135，即對應的C為135。

所以進度 - 成本經過優化的各工序壓縮時間為：x1=3，x2=0，x3=3，x4=0，x5=0，x6=1，x7=0，x8=3，相應的直接壓縮費用為：135元。

3.3 結果分析

根據表3，由擬合各工序壓縮時間與直接壓縮費用關系的GA-BP神經網絡測試結果可知，最小測試結果相對誤差為0.88%，最大測試結果相對誤差為7.70%，因此，所有測試結果的相對誤差均控制在10%以內[22]，且相對誤差平均值=(0.88%+5.50%+1.11%+4.38%+3.63%+2.94%+7.70%+3.70%)/8=3.73%，這表明了GA-BP神經網絡的實際輸出值與期望輸出值較為接近，從而訓練好的GA-BP神經網絡能夠較為準確地表達進度和成本之間的關系。

算例中，運用遺傳神經網絡和免疫粒子群算法的組合方法尋優結果為(x1,x2,x3,x4,x5,x6,x7,x8)=(3,0,3,0,0,1,0,3)，對應的直接壓縮費用是137.52元。基于數學模型的單純形法求解結果為(x1,x2,x3,x4,x5,x6,x7,x8)=(3,0,3,0,0,1,0,3)，對應的直接壓縮費用是135元。基于遺傳神經網絡和免疫粒子群算法的尋優結果相對于單純形法求解結果的相對誤差為1.87%。所以，基于遺傳神經網絡和免疫粒子群算法的組合方法是可以較為準確地解決進度 - 成本優化問題。另外，由圖2可知，基于遺傳神經網絡和免疫粒子群算法的尋優在第10次迭代之前就已經接近最優結果，說明該組合方法尋優效果較好。

綜合以上分析，對于復雜工序的地鐵隧道施工進度 - 成本優化，為了避免數學公式不能準確表達或者無法表達進度成本之間的關系，就可以采用基于遺傳神經網絡和免疫粒子群算法的組合方法進行求解。

4 結 論

(1)對于施工工序較多的地鐵隧道施工進度 - 成本優化問題，本文提出了基于遺傳神經網絡和免疫粒子群算法的組合方法解決進度 - 成本優化問題，并構建了該組合方法求解進度 - 成本優化問題的模型。

(2)基于算例，采用基于遺傳神經網絡和免疫粒子群算法的組合方法以及單純形法分別進行進度 - 成本優化。通過結果對比分析，得出了該組合方法可以較為準確地實現進度 - 成本優化。

(3)大型地鐵隧道施工項目進度 - 成本優化時，數學公式通常比較復雜或者無法用數學公式準確表達。因此，基于遺傳神經網絡和免疫粒子群算法的組合方法為此類問題提供了一個新的解決方法。