山東近海海水COD與BOD相關性研究*

王煥卿，馮巍巍,3**，蔡宗岐，侯耀斌,3，劉增東

(1.中國科學院煙臺海岸帶研究所，中國科學院海岸帶環境過程重點實驗室，山東煙臺 264003;2.中國科學院海洋大科學研究中心，山東青島 266071;3.中國科學院大學，北京 100049;4.煙臺市環境監測中心站，山東煙臺 264000)

0 引言

水體中的有機污染物對環境危害較大[1]。這些有機污染物來源有兩部分，一部分是天然有機污染物質，另一部分來源于工業、生活等行業產生的多種有機污染物質[2]。這些有機污染物在對環境的影響和污染危害方面可分為易被生物降解的和不易被生物降解的；其中易被生物降解的有機污染物包括碳氫化合物、蛋白質、脂肪等；不易被生物降解的有機污染物包括酚、苯、多環芳烴等。

水體中的化學需氧量(COD)、生化需氧量(BOD)不僅是環境檢測的重要指標，對預防、觀測赤潮等水污染現象具有重要意義[3]，而且還是生化降解、生化反應以及生化處理流程設計和動力學研究等方面的重要參數[4]。目前COD與BOD的檢測方法大多停留在傳統的化學方法上，雖然化學方法檢測結果比較準確，但是仍然存在分析時間長、二次污染嚴重等缺點[5]。尤其是BOD的測定，因為生化反應較為緩慢，所以完成測定需要較長的時間(一般為5日)，具有較大的延遲性，給水質環境檢測中需要快速檢測的場合帶來了較大的不便。

一般來說，在水體環境相對穩定的條件下，COD與BOD存在一定的相關性。但是在實際海水中，COD與BOD的相關性關系受環境、氣候、地理位置、溫度、溶解氧等多種因素影響。研究水體中COD含量與BOD含量的關系，對通過水體的COD計算BOD有一定的指導意義[6]，尤其對現場實時監測具有很大的應用價值。為此，本研究以山東沿海不同地區實驗站點的COD、BOD、溶解氧、溫度數據為基礎進行數學建模，通過最小二乘法線性擬合找出COD與BOD關系模型。將此模型與COD光學傳感器結合起來，可以在得出被測水體COD的同時計算出BOD，為海水水質環境BOD檢測提供新的方法和手段。

1 模型建立

1.1 COD與BOD關系的數學模型

COD測定的水體有機物包含BOD測定的水體有機物，因此從宏觀方面分析水體中COD與BOD確實存在一定關系。水體中COD與BOD含量受多種因素的影響[7]，在有機質成分組成相對穩定的水體中，COD與BOD的比例關系比較穩定[8]。化學過程中消耗的溶解氧含量包含生化過程中所消耗的溶解氧數量[9]，所以COD可以分為兩部分，一部分與BOD重疊，另一部分不與BOD重疊[10]。

上述分解過程可以用下式表達：

COD=CODi+CODe，

(1)

其中，CODi表示COD當中與BOD重疊的部分，CODe表示COD當中不與BOD重疊的部分。

BOD來源分為兩個部分：第一部分是在BOD反應過程，微生物氧化所吸收有機物而使用的氧量，用OA代表；第二部分是在BOD反應過程，微生物自身的細胞物質在生長繁殖中參與氧化反應(內源呼吸)所使用的氧量，用OB代表。所以有機物完全生化需氧量BODn可以用下式表示：

BODn=OA+OB，

=A×CODi+B×C×CODi，

=(A+B×C)×CODi，

(2)

式中，A為OA在CODi中所占比例；B×C為OB在CODi中所占比例。

BODn=BOD÷E，

(3)

式中，E為與耗氧有關的常數。

所以，

CODi=BOD÷[E×(A+B×C)]，

(4)

故

COD=BOD÷[E×(A+B×C)]+CODe。

(5)

令

K=1/[E×(A+B×C)]，則可以導出COD與BOD關系的方程式

COD=K×BOD+CODe。

(6)

對于有機質成分組成相對穩定的水體，(6)式中的K值與CODe值都具有確定性，所以從數學理論上來說COD與BOD具有線性相關性[11]。

1.2 最小二乘法擬合數學模型

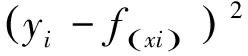
將該算法應用于COD與溫度、溶解氧、BOD相關性分析中，能夠快速、高效地求出擬合函數，進行回歸分析。具體計算步驟如下：

假設COD與溫度(T)、溶解氧(DO)、BOD之間的函數關系式為

COD=a1T+a2DO+a3BOD+b1，

(7)

則擬合誤差

(8)

若要找出最優擬合曲線，只需找到a1、a2、a3和b1參數的組合，使得e誤差最小。

對誤差e求偏導，令其等于零：

(9)

求解(9)式可得a1，a2，a3，b1，將結果代入(7)式可得擬合函數。

1.3 實驗數據來源

為實際說明BOD和COD的相關性，選取山東沿海地區海水的COD和BOD數據深入分析。這些實驗數據來源于煙臺市環境監測中心站，海水監測站點分布于招遠、蓬萊、海陽等沿海地區。COD的測量方法采用高錳酸鉀氧化法[12]，BOD的測定采用水質五日生化需氧量測定法[12]，溶解氧采用碘量法[13]，溫度值用數字溫度計測量。各站點的海水COD、BOD、溫度、溶解氧由煙臺市環境監測中心站工作人員在同一時間多次測量，其中部分站點數據如表1所示。針對表1中的數據，以溫度、溶解氧、BOD作自變量，COD作因變量，對COD與溫度、溶解氧、BOD做多元線性擬合。利用最小二乘法，找出最優擬合值和最優擬合參數，并進行多元回歸分析。

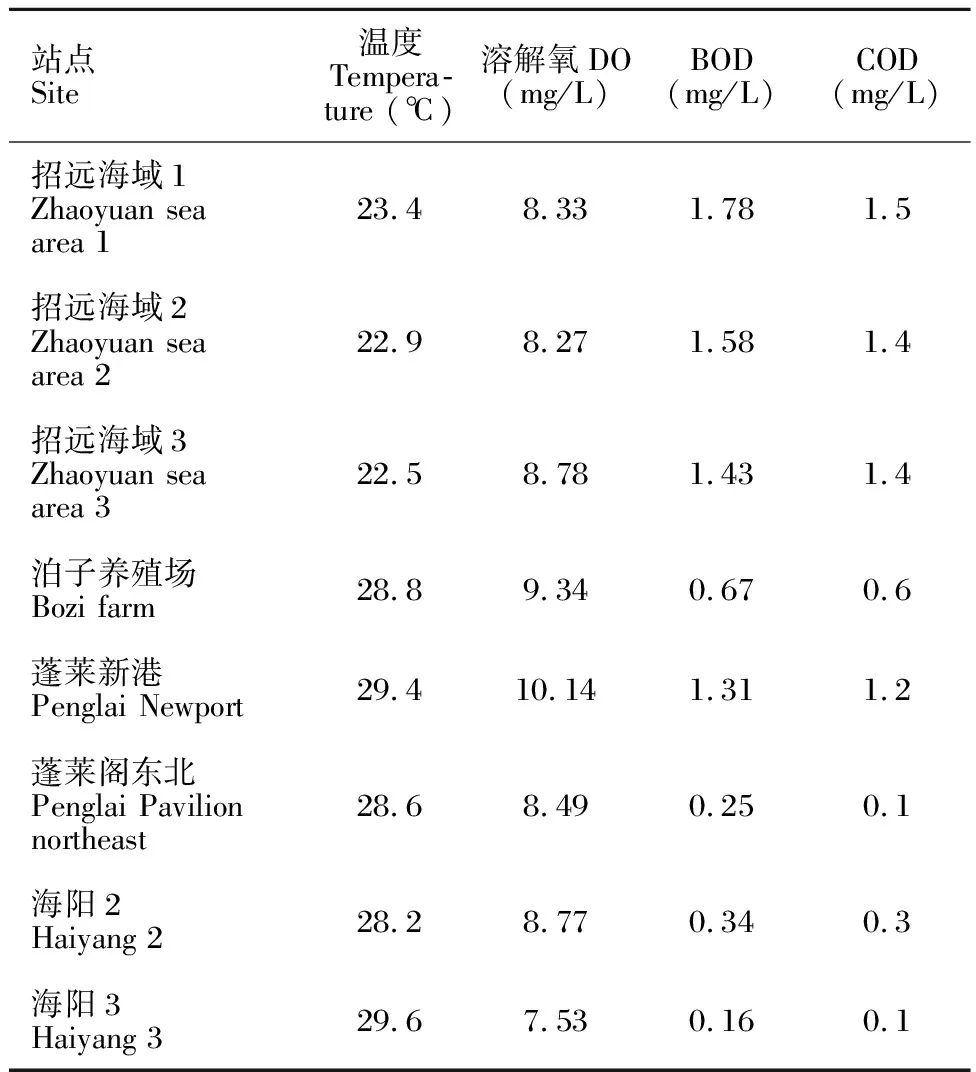
表1 山東沿海地區各實驗站點溫度、溶解氧、BOD、COD測量數據

2 結果與分析

對表1中的數據進行多元回歸分析后，得出COD與溫度、溶解氧、BOD存在以下關系，其中R2為0.959 82。

BOD=-0.00414×T+0.04438×DO+

0.92421×COD-0.38244。

(10)

經多元回歸分析后，可知COD與溫度、溶解氧、BOD存在線性關系。對得到的回歸方程分別做F檢驗和殘差分析，結果表明變量間線性相關關系較為顯著，所擬合的線性回歸方程達到較高的置信度，殘差隨機分布在等于0的直線上下，擬合效果良好。

在以上分析結果基礎上做簡化，忽略掉溫度、溶解氧的影響，只對COD與BOD用最小二乘法做一元線性擬合，并進行一元回歸分析，得到COD與BOD的關系如下，其中R2為0.948 6。

BOD=0.93727×COD-0.06458。

(11)

上式中海水COD與BOD的相關系數為0.948 6，說明COD單純與BOD之間也存在較好的線性關系，可以滿足實際應用。

利用建立的COD和BOD之間的一元回歸方程，以及已有的COD和BOD數據，利用COD反演BOD，得到每組BOD實測值與預測值之間的相對誤差(圖1)，29組數據BOD實測值和預測值的相對誤差最大不超過35%，除去個別點位，相對誤差基本在15%以下。因此，應用得到的模型可以很好地利用COD值來預測BOD，進一步證明該方法的可行性及可靠性。

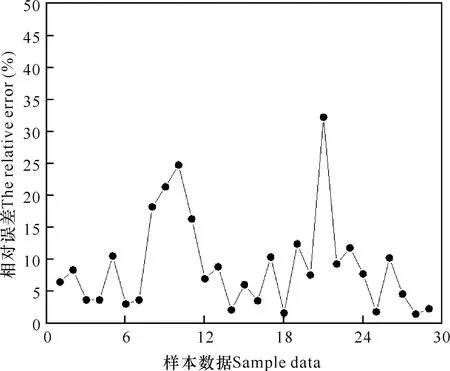
圖1 海水BOD實測值與預測值的相對誤差

3 結論

根據上述一元回歸分析可知，海水COD與BOD存在一元函數關系，該關系表明，在水質條件一定的情況下，上述區域海水COD與BOD存在較好的線性關系。因此，可以根據海水COD推算出海水BOD，為水體BOD的快速檢測提供新思路。

此關系可拓展應用范圍，應用到相關的光學法COD檢測設備上，在測得海水COD的同時，快速推算出該海水的BOD。從應用層面講，該類方法的準確性取決于實驗數據的完備性。但是，由于不同地區的地理環境、氣象條件和水文情況存在差異，水中的有機物含量也存在一定改變，因此不同地區海水COD與BOD的關系可能存在差異。所以用海水COD推算BOD時，需要針對不同情況相應地修正系數，以適應實際情況，做出準確測量。