基于連續動態時間規整算法的工業機器人軌跡準確度分析

李 睿，王炳榮，崔曉玲

（北京工業大學北京市精密測控技術與儀器工程技術研究中心，北京100124）

1 引 言

工業機器人是智能制造的關鍵裝備之一，隨著工業機器人在精密制造、航空航天、精密測量等高精度領域應用的不斷增加，對機器人的運動性能要求也越來越高［1］。機器人軌跡準確度和重復性指標是衡量機器人性能最關鍵的指標之一，國際標準ISO 9283（Manipulating industrial robots-Performance criteria and related test methods）［2］，國標GB/T 12642-2003：工業機器人性能規范及其試驗方法［3］，歐洲工業機器人標準改進項目［4］（IRIS）以及美國國家標準ANSI/RIA R15.05-2-1992：Path-Related and Dynamic Performance Characteristics Evaluation［5］，均對機器人軌跡準確度和重復性測試方法進行了定義。

目前，以上3 個標準廣泛被應用于工業機器人軌跡性能測試中。根據國際標準ISO 9283 中對位姿精度的試驗規范和要求，韓國機器人工業發展研究所采用激光跟蹤測量系統［5］對工業機器人進行基于D-H 模型的運動學參數標定；天津大學采用雙目視覺系統［6］對工業機器人進行了位置誤差標定。北京工業大學在國標GB/T 12642-2013 的基礎上，分析工業機器人每一項運動性能的定義和物理意義并開發了一套性能測試與評價軟件［7］。伊朗科技大學基于美國ANSI/RIA R15.05-2-1992 標準開發了一套基于視覺的工業機器人控制系統，完成了對工業機器人的軌跡性能測試［8］。

ISO 9283 和GB/T 12642 標準中，規定需構造垂直于指令軌跡的法平面，與實際軌跡相交計算軌跡準確度，并制定了試驗方法，但標準中沒有具體規定法平面構造的位置，僅說明選擇時應與測量形狀和速度相關。ANSI/RIA 中規定在指令軌跡上等距構造法平面，然而對于非直線軌跡，受機器人的運動速度和運動偏差、測量系統的采樣頻率和測量誤差的影響，軌跡上各點法線不斷變化，構造的法平面可能相交，導致指令軌跡與實際軌跡點之間產生錯誤的映射，造成較大的測量誤差。

針對非直線軌跡法平面構造時，受機器人運動速度和運動偏差、測量系統的采樣頻率和測量誤差的影響，導致指令軌跡與實際軌跡點之間出現映射錯誤，造成較大的軌跡測量誤差的問題，本文提出了采用連續動態時間規整算法（Continuous Dynamic Time Warping，CDTW）解決機器人軌跡映射的問題，通過對工業機器人軌跡準確度進行測量分析，與國際標準ISO 9283 中的評價方法進行對比，并著重分析了機器人運動速度以及測量系統采樣頻率對軌跡映射方法的影響，驗證了動態時間規整方法（Dynamic Time Warping，DTW）應用于軌跡準確度分析的有效性和正確性。

2 機器人運動特性的測試評價方法及問題分析

國際標準ISO 9283 中規定，工業機器人軌跡準確度由指令軌跡的位置與各實到軌跡位置集群中心線之間的偏差決定，如圖1 所示。

沿指令軌跡選擇m個點并計算其法平面，n條實測軌跡與法平面交點坐標的平均值與指令軌跡的距離的最大值ATP為位置軌跡準確度：

圖1 ISO 標準的軌跡準確度Fig.1 Path accuracy of ISO standard

美國標準ANSI/RIA R15.05-2-1992 與ISO 9283 的軌跡準確度試驗標準相類似，規定了法平面的放置位置，如圖2 所示。標準規定指令軌跡必須是二維的，位于標準測試平面XOY上，此標準測試平面為參考平面，取決于機器人的工作空間，L為標準測試平面的寬度。法平面與標準測試平面法線對齊，并在參考軌跡上等距放置。通過法平面與指令軌跡和實測軌跡的交點來計算軌跡誤差。然而在非直線軌跡的情況下，法平面仍然會交叉并使時間序列顛倒，造成軌跡點之間的錯誤映射，并且此法平面的構造放置方式無法對尖銳拐角點進行映射。

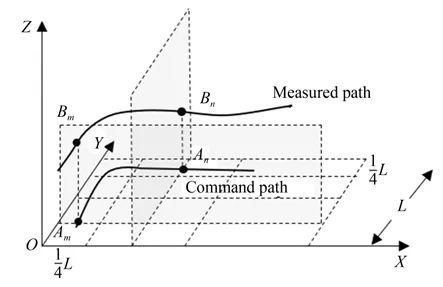
圖2 美國標準的軌跡準確度Fig.2 Path accuracy of ANSI

歐洲機器人工業標準改進項目（IRIS）規定在實測軌跡的每個采樣點處構造與軌跡切線垂直的法平面。但該方法在軌跡較為復雜的情況下仍然存在局限性，受機器人運動偏差和測量誤差影響，實測軌跡的切線具有不確定性，法平面可能相交，導致時間順序顛倒，造成錯誤的映射，如圖3 所示。圖3（a）為直線軌跡，由于運動偏差或測量誤差的影響，采樣點處的法平面可能相交，導致映射的錯誤，造成微小的軌跡測量誤差。圖3（b）為拐角軌跡，為保證運動的連續平穩，機器人在拐角處的運動軌跡為近似軌跡，實測軌跡的形狀與指令軌跡在拐角處存在一定的偏差，導致明顯的映射錯誤，造成較大的軌跡測量誤差。圖3（c）為一個實際的例子，可以看到，拐角處實測軌跡為接近過渡方式，在拐角處實測軌跡采樣點的法平面與指令軌跡相交于明顯錯誤的位置甚至不相交，造成極大的軌跡測量誤差，在拐角軌跡與直線軌跡的相交處容易發生圖3（a）所示的映射錯誤。

圖3 切線法平面存在的映射問題Fig.3 Problem of tangent normal plane

工業機器人在空間中的運動軌跡可以看作時間的函數，其軌跡數據可以看作一條時間序列。DTW 算法是一種衡量兩個時間序列相似度的方法，用滿足一定條件的時間規整函數描述兩者之間的時間對應關系，實現兩序列間的最優匹配。因此，針對指令軌跡與實際軌跡采樣點之間的映射關系問題，采用DTW 算法進行研究分析。

3 動態時間規整

DTW 算法是一種具有非線性時間歸一化效果的模式匹配算法［10］，在工業機器人的運動軌跡分析中，本文利用這種算法進行工業機器人實際軌跡與指令軌跡之間的映射，避免出現映射后時間順序顛倒的問題。

3.1 DTW 算法

DTW 算法是一種把時間規整和距離測度計算結合起來的非線性規整技術［11］，通過不斷地計算兩矢量間的距離來搜索兩者之間最優匹配路徑，保證它們之間存在最大的相似度。該算法原理如下：

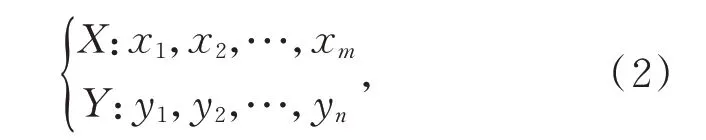
定義兩個離散序列：則，兩個離散序列中各點xi和yj之間的距離：

定義兩者的相似性度量函數D(i，j)，即兩條序列之間的累積距離：

定義規整路徑ω，將序列Y上的數據點非線性地映射到序列X上，使得兩者的累積距離最小：

其中：wT=D(i，j)，ωT是規整路徑ω上的第T個元素，表示xi與yj建立的對應關系。

回溯法［12］是一種選優搜索方法，按選優策略向前搜索，以達到目標，本文選用回溯法得到規整路徑ω。規定規整路徑ω的回溯優選策略為：

（1）邊界性：規整路徑ω要從點(xm，yn)開始，到點(x1，y1)結束；

（2）單調連續性：規整路徑ω從點(xm，yn)開始，只能去往(xm，yn-1)或(xm-1，yn)或(xm-1，yn-1)。

通過上述約束條件可以找到一條累積距離最小的規整路徑，此時序列X和Y之間即可實現最優匹配。采用動態時間規整算法對兩條二維軌跡進行映射分析，結果如圖4 所示。圖4（a）的坐標軸分別表示兩條軌跡的采樣點，網格表示兩條軌跡全部采樣點之間的所有可能映射，每個網格點的數值代表兩點間的相似度量值，通過回溯法的優選策略得到最優規整路徑，根據序列間的規整路徑得到圖4（b）中兩條軌跡的映射關系。

圖4 動態時間規整算法的軌跡映射示例Fig.4 Path mapping example of DTW

3.2 CDTW 算法

將DTW 算法應用于機器人運動分析的一個主要缺點是映射的離散化［13］。機器人在運動時的軌跡是連續的，但軌跡測量數據是離散的，離散的數據導致在應用DTW 算法進行軌跡映射時只能映射到已有的數據點，這種匹配導致兩條軌跡間的相似性度量值增大，點與點之間的匹配度降低，可能出現數據點之間多對一的情況。當采樣頻率較小時，這種現象更加明顯。

CDTW 算法的目標是找到最佳的連續規整路徑，即規整路徑不再被約束為通過圖中的節點，可以映射到兩個連續數據點之間的插值點［14］。不同映射方法獲得的規整路徑對比如圖5所示。

圖5 DTW 與CDTW 映射對比Fig.5 Mapping comparison between DTW and CDTW

與DTW 算法的回溯優選策略不同，CDTW算法的連續性不再局限于網格上的節點，路徑匹配規則如圖6 所示。圖6（a）為采用DTW 算法，規定規整路徑ω只能去往3 個邊界點，圖6（b）為采用CDTW 算法，規整路徑ω可以到達網格的左方和下方中行列之間的插值點。

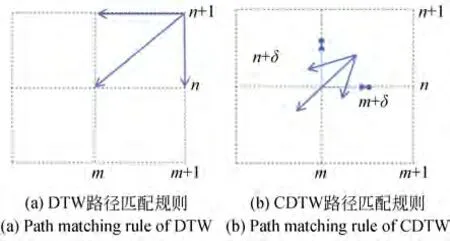
圖6 DTW 與CDTW 路徑匹配規則對比Fig.6 Comparison of Path matching rule between DTW and CDTW

因此，兩序列之間的相似性度量函數表示如式（6）所示：

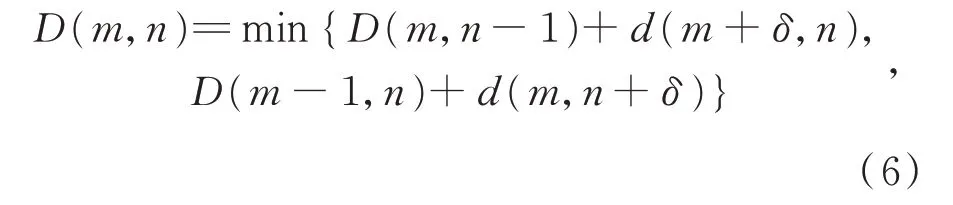
其中，δ為介于0～1 之間的一個參數。δ非零時，一條軌跡的對應點必定位于另一條軌跡上的插值點，可以通過線性插值模型計算具體位置［15］。對于兩條待映射的軌跡曲線C1和C2，通過弧長參數化來描述線性插值模型，曲線上的插值點分別對應r1和r2，如圖7 所示。

圖7 曲線參數化Fig.7 Curve parameterization

曲線C1和C2的點坐標方程式Ck為：

其中：

通過確定r1，r2即可獲得插值點的具體位置。當CDTW 算法進行回溯時，相似性度量矩陣D(i，j)中如果出現多點映射一點的情況，通過線性插值模型在多對一映射的數據點之間進行插值，直到數據點間實現一一映射。通過CDTW算法得到的規整路徑更平滑，能夠更好的反映測量軌跡與指令軌跡點之間的映射關系。機器人在執行拐角軌跡過程中速度會發生變化，因此在數據點相較稀疏的區域進行選擇性的插值處理來提高算法的精度。

4 機器人運動軌跡測量

本文采用Leica 激光跟蹤儀對KUKA KR6 R700 工業機器人進行軌跡測量實驗，參照ISO 9283 標準中提供的可選用的試驗軌跡規劃機器人運動軌跡，試驗裝置如圖8 所示。

圖8 試驗裝置圖Fig.8 Test device

機器人的實際軌跡為時間的函數，因此與其對應的理論軌跡也應該是與時間相關的一條軌跡數據點，而非等間隔采樣的數據。根據在示教器上輸入的指令軌跡，機器人系統生成一條理論軌跡點，該理論軌跡是時間的函數，可以通過上位機與機器人通信實時獲得理論軌跡數據。機器人的運動控制是由機器人的內部控制環境KRL（KUKA Robot Language）與RSI（Robot Sensor Interface）來實現的，KRL 是機器人控制編程接口，主要對實現機器人的非實時控制，在KRL 環境中編寫運動軌跡程序。RSI 是機器人通信接口，實現與外部系統進行數據交互，通過上位機編程對RSI 對象進行配置和調用便可實現機器人運動數據的獲取。本文通過RSI 讀取機器人理論軌跡，通過外部測量設備激光跟蹤儀測量機器人的實際軌跡。

4.1 機器人通信

RSI 可通過Ethernet 通信或機器人總線IO與外部系統實現數據交互，具備周期性的信號處理和評估能力。RSI 每隔12 ms 進行一次數據交互，實時性較好。上位機與機器人控制器進行的數據交換是以XML 格式進行的，通信前的參數配置如圖9 所示。

圖9 XML 文件配置Fig.9 XML file configuration

RSI 上下文是在KRL 程序中被加載的，其對信號的處理與KRL 程序并行執行，并可按需要激活或取消激活。RSI 在KRL 程序中調用的流程為：聲明KRL 變量，創建RSI 上下文，將配置的參數加載到RSI 容器中。激活RSI，上位機建立與機器人系統的通信，機器人執行運動軌跡，上位機周期性的獲取機器人的實時數據，軌跡執行結束后關閉RSI。

4.2 機器人與激光跟蹤儀坐標系變換矩陣標定

機器人基坐標系和測量坐標系的轉換可以通過測量機器人安裝平面及軸1，2 軸線擬合計算，但機器人運動學參數誤差會影響坐標系轉換的準確性，因此本文采用D-H 模型對機器人運動學參數進行標定［16］，利用標定后的參數精標定坐標系轉換矩陣，提高測量精度。

利用激光跟蹤儀獲得機器人末端靶標位置，采用位置誤差最小模型解算機器人的運動學參數，以測量的位置與實際位置之間的差值最小為約束條件來求解參數，坐標系轉換關系如圖10所示。

圖10 坐標系轉換關系Fig.10 Coordinate system conversion

激光跟蹤儀與機器人坐標系轉換存在3 個旋轉誤差δx，δy，δz以及3 個平移誤差dx，dy，dz。兩坐標系的轉換矩陣誤差可由如式（8）表示：

將靶球剛性連接在機器人末端，相對于末端只發生了平移變換，誤差關系式為：

建立測量得到的靶球坐標系Otm與計算得到的靶球坐標系Otc的關系式：

至少選取測量11 個位置坐標用于標定，并利用最小二乘法進行求解。標定后機器人的坐標系轉換矩陣誤差及靶球安裝誤差如表1所示。

表1 坐標系轉換矩陣誤差及靶球安裝誤差Tab.1 Coordinate system transformation matrix error and target ball installation error（mm）

5 機器人軌跡準確度試驗

根據ISO 9283 標準附錄中的可選測試軌跡數據集編輯一條軌跡，該軌跡位于標準測試平面內，包括直線、圓弧和拐角運動的組合。機器人首先執行一段直線軌跡，起點P1坐標為（400，-50，750），P2為（450，-50，750）。其次執行一段圓弧類型的圓滑拐角，設置拐角為5 mm。最后執行一段直線軌跡，終點P3為（450，0，750）。上位機實時讀取機器人系統的理論軌跡，激光跟蹤儀讀取機器人的實際運行軌跡，通過坐標系變換轉換到同一坐標系下。

5.1 直線軌跡映射方法對比

為了比較ISO 標準規定方法、DTW 算法以及CDTW 算法的映射結果，設置激光跟蹤儀采樣頻率為50 Hz，首先選取了直線軌跡處的30對數據點。采用ISO 標準方法和DTW 算法進行映射，軌跡映射對比分析如圖11 所示，計算直線軌跡映射后的軌跡準確度結果如圖12所示。

圖11 直線軌跡映射結果Fig.11 Comparison of linear path mapping result

圖12 直線軌跡準確度計算結果Fig.12 Calculation results of linear path accuracy

圖11 中的直線軌跡，機器人的運行速度相對穩定，采樣點比較均勻，ISO 方法獲得的軌跡準確度為0.312 mm，DTW 算法獲得的軌跡準確度為0.306 mm。軌跡準確定測量精度為0.01 mm，兩種算法計算結果相差0.006 mm，相對誤差1.9%，計算結果相一致，說明采用映射算法對軌跡準確度的計算結果是正確的。

5.2 拐角軌跡映射方法對比

選取拐角處的50 對數據點，采用3 種方法分別對兩種軌跡的數據點進行映射。對于ISO 標準中的法平面放置問題，采用文獻8 的方法優化。軌跡映射對比如圖13 所示。

圖13 拐角軌跡映射結果比較Fig.13 Comparison of corner path mapping result

圖13 中可以看到，在機器人執行拐角軌跡時，受機器人運動速度以及機器人運動偏差的影響，導致實際軌跡的形狀與指令軌跡存在一定的差別，圖13（a）中的ISO 軌跡映射方法在點21 至點30 處的10 個點存在時間序列的失真，占軌跡總點數的20%，導致映射的錯誤，嚴重影響軌跡準確度評價的正確性。圖13（b）中的DTW 算法則不會產生這種問題，能夠正確地進行軌跡點之間的映射。但由于采樣頻率的限制，在理論軌跡點14，17，21，31，35，37 處存在非一一映射的現象，占總點數的12%，導致軌跡準確度的不準確。圖13（c）中采用CDTW 算法不僅不會產生映射錯誤問題，由于內插點的存在，實際軌跡點能夠映射到理論軌跡的非參考點上，不會出現一點映射多點的情況。計算拐角軌跡映射后的軌跡準確度結果如圖14 所示。

圖14 拐角軌跡準確度計算結果Fig.14 Calculation results of corner path accuracy

ISO 的方法測量得到的軌跡誤差值大，與圖13（a）對比分析可知，點21 至點30 的測量誤差是由于ISO 方法的映射錯誤導致的。DTW 算法明顯減小了映射后的軌跡準確度，與圖13（b）對比分析可知，曲線的4 個峰值點是由于采樣頻率的限制導致數據點之間發生多對一的映射導致的。CDTW 算法通過內插點解決了此問題，誤差曲線更光滑，提高了軌跡準確度。采用ISO 方法計算得到的軌跡準確度為1.343 mm，標準差為0.389 mm；采用DTW 算法計算得到的軌跡準確度為0.585 mm，標準差為0.194 mm；采用CDTW 算法計算得到的軌跡準確度為0.357 mm，標準差為0.054 mm。CDTW 算法映射后的軌跡準確度提高73%，標準差減小86%，誤差整體波動幅度明顯變小。

5.3 機器人運動速度對映射的影響

ISO 9283 中規定，機器人軌跡準確度的測試應與軌跡速度相關，因此選擇機器人運行速度50%和100%，分析不同速度下DTW 和CDTW算法對測量精度的影響。選擇激光跟蹤儀采樣頻率保持50 Hz，獲得兩組軌跡數據，取得拐角處的57 對數據點和30 對數據點，代入DTW 算法和CDTW 算法，分析機器人運動速度對映射方法的影響。不同速度下DTW 算法和CDTW 算法的映射結果如圖15 所示。

圖15 不同速度下的DTW 算法和CDTW 算法的映射結果Fig.15 Mapping results of DTW and CDTW algorithm at different speeds

由圖15 可知，由于機器人運動偏差的影響，機器人執行拐角運動時存在過沖和超調，速度越快機器人運動偏差越大，同時，相同采樣頻率下，運動速度越快采樣點個數越少。對比50% 和100%速度下DTW 算法映射的結果，可以看到數據點映射時都會出現多對一的情況，但隨著速度的降低，數據點的增加，數據點多對一的映射情況減少。對于50%和100%速度下的CDTW算法，由于CDTW 能夠進行數據點之間的插值，因此不會受到數據點密度的影響。映射后的軌跡準確度對比分析如表2 所示。

表2 不同速度下的兩種算法的軌跡誤差對比Tab.2 Comparison of path error between DTW and CDTW algorithm at different speeds（mm）

由表2 可知，當速度相同時，CDTW 算法相比于DTW 算法軌跡準確度提高了40%。當速度降低時，CDTW 算法標準差減小54%，DTW算法標準差減小34%，CDTW 算法能夠更好地降低誤差整體波動幅度。

5.4 測量系統采樣頻率對映射的影響

為了分析測量系統的采樣頻率對映射的影響，設置激光跟蹤儀采樣頻率分別為25 Hz，50 Hz 和80 Hz，獲得兩組軌跡數據，分別取得拐角處的20 對數據點、40 對數據點和68 對數據點，代入ISO 算法、DTW 算法和CDTW 算法，分析采樣頻率對3 種映射方法的影響。實驗結果如表3所示。

采用ISO 算法進行軌跡間的映射，隨著采樣頻率的增大，采樣點之間的距離間隔變小，軌跡切線變得陡峭，出現映射錯誤的軌跡點增多。由表3 可知，當采樣頻率從25 Hz 增加到80 Hz 時，軌跡準確度從1.160 mm 降低到1.532 mm，標準差從0.304 mm 增大到0.535 mm。采樣頻率的提高導致ISO 算法映射后的軌跡準確度降低，誤差整體波動幅度增大。

表3 不同頻率下3 種算法的軌跡誤差對比Tab.3 Comparison of path error of three algorithms at different frequencies（mm）

DTW 算法是點對點之間的映射，隨著采樣頻率的提高，軌跡點密度增大，軌跡點之間能夠更好地實現一對一的匹配。通過表3 則可以看出采用DTW 映射方法與ISO 映射方法正好相反，當采樣頻率從25 Hz 增加到80 Hz 時，軌跡準確度從0.678 mm 提高至0.508 mm，標準差從0.242 mm 減小至0.159 mm。采樣頻率的提高導致DTW 算法映射后的軌跡準確度提高，誤差整體波動幅度減小。

對于表3 中的CDTW 算法映射軌跡誤差，當采樣頻率從25 Hz 增加到80 Hz 時，軌跡準確度的極值為0.015 mm，標準差的極值為0.003 mm。由于CDTW 算法采用插值計算，采樣頻率不會對其軌跡準確度造成明顯的影響。

6 結 論

本文提出了一種基于連續動態時間規整方法的工業機器人軌跡準確度分析方法，通過對兩軌跡序列的相似度最優匹配進行映射，對采樣數據點建立插值模型來提高軌跡點之間的映射準確度，解決了不同速度和復雜軌跡測量中由于映射錯誤導致的軌跡準確度評價不準確的問題。

采用激光跟蹤儀測量機器人的運動軌跡，針對直線軌跡與拐角軌跡將該方法與ISO 標準方法進行對比分析，并分析了機器人運動速度和測量系統的采樣頻率對算法的影響。實驗結果表明：ISO 標準方法和DTW 算法能夠很好地應用在直線軌跡準確度評價中，對于拐角軌跡ISO 方法出現明顯的映射錯誤，DTW 算法解決了映射錯誤，但受機器人運動速度和測量系統采樣頻率的影響存在多點映射的問題，CDTW 算法有效解決了此問題，提高了軌跡準確度。