基于多核處理器BWDSP1042的FFT性能優化 *

藺麗華，李 敏 ，蘇 濤，張美春，王佳儀

(1.西安科技大學 通信與信息工程學院，西安 710054；2.西安電子科技大學 雷達信號處理國家重點實驗室，西安 710126)

0 引 言

快速傅里葉變換(Fast Fourier Transform，FFT)廣泛應用于信號、音頻、圖像等領域的科學計算與處理，是這些領域時頻轉換的基本研究工具[1]。FFT算法性能的優劣代表著DSP芯片處理能力的高低，FFT運算時間作為表征芯片性能的重要參數，各領域對于FFT計算與處理的實時性要求也越來越高[1-2]。

為響應國家大力發展國內集成電路產業的號召，打破國外的高計算性能領域的核心技術對我國的壟斷，中國電科38所自主研發了一款具有自主知識產權的BWDSP產品。BWDSP1042[3]是一款運算速度快、功耗低、實時性強、便攜的高性能雙核DSP，又名“魂芯二號“，其底層架構、指令集和集成開發環境ECS都是38所自主設計與研發的。BWDSP1042是在第一代產品BWDSP100[4]的基礎上所開發的，仍然是16條發射超長指令字(Very Long Instruction Word，VLIW)和4路單指令流多數據流(Single Instruction Multiple Data，SIMD)混合架構的數字信號處理器，但內核升級為eC104+，擴展了指令集，優化了存儲空間，執行部件提升了運算性能，在物理存儲空間上劃分了程序空間和數據空間。

本文基于BWDSP1042的體系結構和指令編排，在開發環境ECS下完成FFT帶有C程序調用接口的匯編程序，基于按時間抽選的基-2 FFT[5]算法進行結構優化，通過多階合并、指令并行、循環展開、軟件流水和高效尋址指令等方式進行并行計算，使用匯編程序的實際運行周期來衡量算法優化程度，并與BWDSP100和TMS320C6678函數庫中的FFT做對比，使用Matlab程序驗證本文匯編程序的正確性，按照誤差閾值來判定FFT算法功能編寫是否準確。研究結果表明，512點、1 024點、2 048點定點復數FFT算法的實際運行周期分別為571、991、2 112，比BWDSP100函數庫中的FFT分別提升了1.12倍、1.18倍、1.27倍，比C6678函數庫中的FFT分別提升了1.32倍、1.40倍、1.88倍。本文研究的基于BWDSP1042的FFT算法計算速度快，實時性高，對支持國產芯片BWDSP1042的商業應用具有一定的實際意義。

1 基于BWDSP的FFT算法優化

1.1 基-2時間抽取FFT算法

快速傅里葉變換是離散傅里葉變換(Discrete Fourier Transform,DFT)的一種快速計算形式，可以很明顯地減少計算量和運算時間。DFT正變換公式如式(1)所示:

(1)

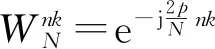
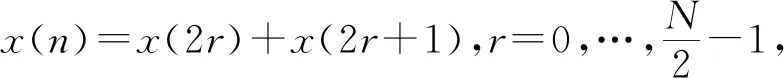
(2)

N點的FFT算法一共有m階的蝶形運算，每一階都有N/2形結構參與運算，每個蝶形運算(a+bj)(wr+jwi)需要一次復數乘法和兩次復數加法，如圖1所示，每一階的蝶形運算共需要N/2次復數乘法和N次復數加法，所以一個N點的完整FFT運算需要(N/2)m=(N/2)lbN次復數乘法和NlbN次復數加法，時間復雜度為o(NlbN)。但是參與蝶形運算的數據需要從內存中讀取兩個輸入數據和相應的旋轉因子，然后將計算結果寫入到寄存器中，讀取和存放的數據量是一樣的，并不能充分使用BWDSP硬件資源，運算時間也得不到減少。

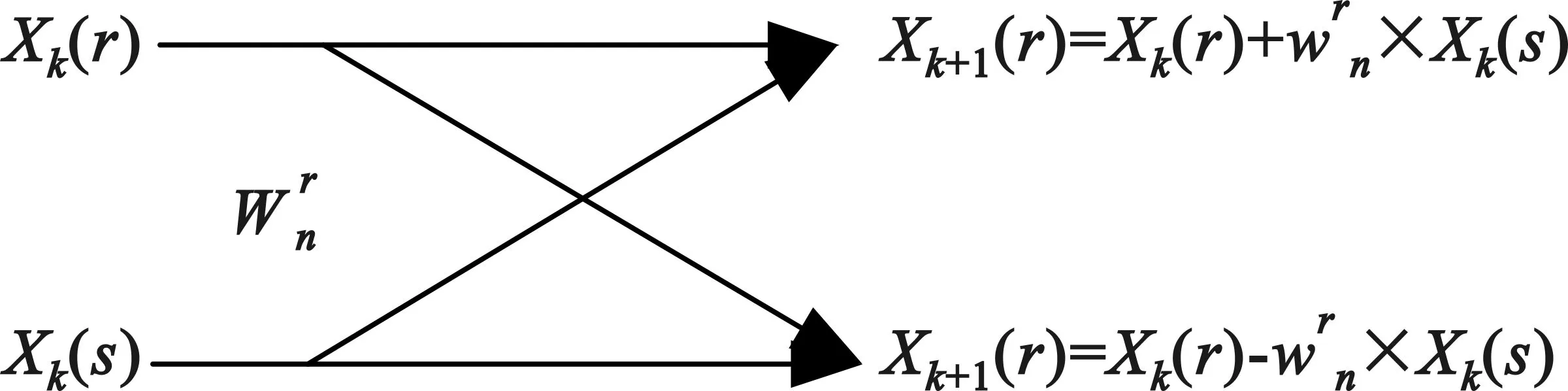
圖1 基-2時間抽取FFT蝶形運算單元

1.2 并行結構FFT優化

在按時間抽選的基-2 FFT算法中，每級任意兩個蝶形運算都是互相獨立的，在正確讀取其旋轉因子的情況下，蝶形運算單元順序可以并行執行。為了充分利用BWDSP1042的SIMD和VLIW混合架構，減少FFT算法的運算時間，在時間抽選的基-2 FFT算法基礎上進行結構調整，使用倒位序輸入、自然序輸出的FFT算法進行蝶形運算單元的并行處理，如圖2所示。BWDSP中數據存儲器劃分為6個block，每個block大小為256 KB。把旋轉因子與輸入數據保存到不同的 block 塊中，并且使用復數指令、位反序尋址指令、數據存儲器讀寫指令等高效指令的特性來充分利用其帶寬，有效減少旋轉因子重復計算或訪存，在充分發揮處理器優勢的同時又能提高FFT算法性能。按時間抽選的基-2FFT實現的并行計算流程圖如圖3所示。

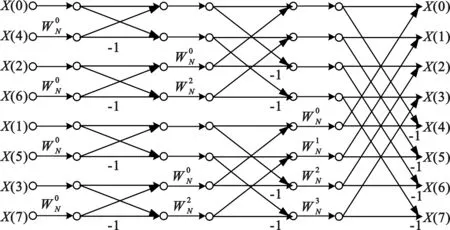
圖2 倒位序輸入、自然序輸出8點FFT流圖

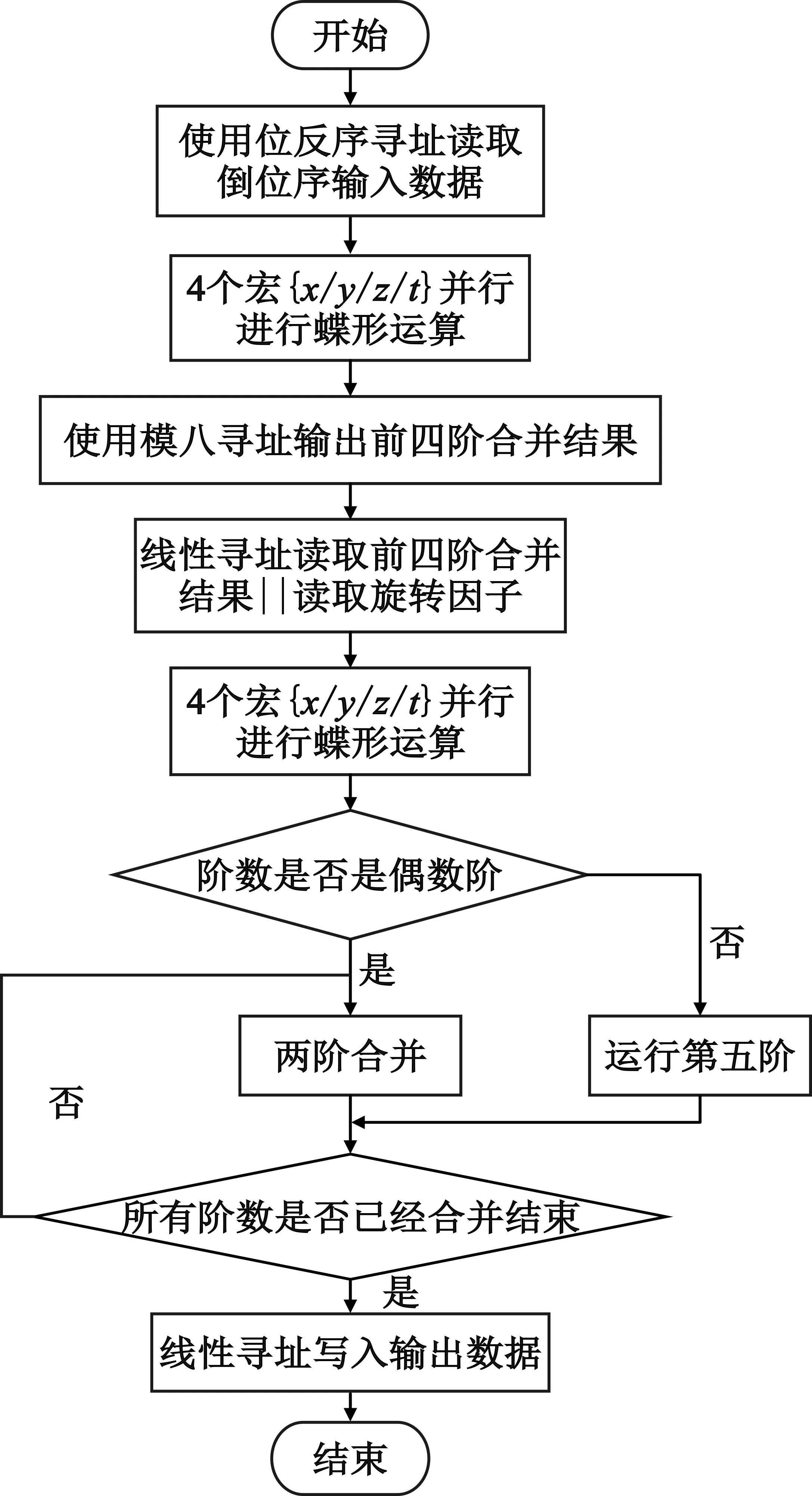
圖3 并行結構FFT流程圖

1.2 1 024點的定點FFT算法優化實現

1.2.1 尋址方式選擇

前四階的蝶形運算合并時使用位反序尋址讀操作、模八雙字寫操作的方式來優化。位反序尋址雙字讀訪存指令來讀取輸入數據，讀取指令為r7:6=br(N)[u0+=1,1]。

在以上這一條讀取指令中，在寄存器r7:6前沒有指定宏,則默認是使用4個執行宏{x,y,z,t}同時讀數，一條指令能夠讀取8個定點數，利用4個執行宏同時讀數可顯著提高運行效率。位反序尋址指令是專門為FFT算法設計的，它能夠將u0的基地址若干位前后顛倒，生成算法所需要的實際地址來進行后續的數據訪存操作，但是，一旦修改過的基地址不參與反序操作，這種位反序方式能夠保證數據訪存的正確性，也提高了數據高效訪存的效率。位反序的位數N是基于N點FFT算法的蝶形運算階數lbN，當階數是偶數階時進行合并前四階，當階數是奇數階時，前四階合并結束后單獨執行第五階運算，其余均是采用兩階合并。

模八尋址方式將前四階合并的計算結果按照順序寫入地址寄存器中，模八尋址指令為m[v0+=v10,v11]=xr41:40yr45:44zr43:42tr47:46。

數據的寫入是根據運算宏通用寄存器堆中的數據按照宏{x,y,z,t}確定好的順序存儲到數據存儲器中的，每條指令中4個宏中的通用寄存器堆的序號可以按照指令確定的數據各不相同。通過模八尋址寫入的方式，能夠改變不同宏之間不同的通用寄存器的值來改變前四階合并結束后計算結果的順序，從而保證輸出的順序是自然序。所以，本文在前四階使用位反序尋址讀操作、模八雙字寫操作，其他階采用線性雙字讀寫操作。只通過優化前四階的尋址方式，是因為已經將倒位序輸入的數據通過模八雙字寫入的操作將數據調整順序，后面的蝶形運算將會按照模八尋址的寫入數據順序進行計算，所以前四階尋址方式優化足以保證輸出順序是自然序，滿足算法要求。

1.2.2 復數運算指令充分利用宏資源

BWDSP1042處理器提供了高效的16位定點復數同時做加/減以及除2操作指令，專門為定點數據運算設定的一種操作方式，大大減少了復數操作的指令周期。

{x,y,z,t}CHRm_Rn =(CHRm +/-CHRn),

{x,y,z,t}CHRm_Rn=(CHRm +/-CHRn)/2。

一個16位定點復數同另一個16位定點復數進行加/減運算，運算結果直接送到結果存儲器，或者除2后送到結果寄存器。通過定點復數指令來實現定點的蝶形運算。xCHRm_Rn=(CHRm+/-CHRn)這條指令只能完成1個定點復數的加減運算，結果存入到xCHRm_Rn寄存器中，而指令CHRs=(CHRm +/- CHRn)能夠計算4個定點復數，分別將結果存入到4個執行宏{x,y,z,t}CHRm_Rn中。對比可知，定點復數進行蝶形運算時，充分利用4個執行宏計算可顯著提高運行效率。

2.2.3 多階合并

傳統算法中，計算完每一階的結果將保存到寄存器中，在下一階運算時通過處理器的尋址方式再將結果讀取出來，在中間結果的寫入和讀取期間進行了大量的數據訪存過程，占用了運行算法大量時間。所以，為了實現高效的訪存，采用多階合并的方式來提升運算效率，減少數據輸入輸出的操作。N點FFT共有lbN階，每階有N/2個蝶形運算，每個蝶形運算需要完成一次復數乘法，兩次復數加法。由于1 024點FFT算法共有10階運算，前四階的旋轉因子較為特殊，不占用乘法器資源，所以蝶形運算只是使用加法器即可。

假設點數N是大于等于64點的，在這里簡單介紹一下多階合并的思路:首先合并前四階，然后根據N點FFT的階數進行分支，若是偶數階，直接跳轉到兩階合并的模塊；若是奇數階，先計算第五階的蝶形運算，再繼續進行兩階合并模塊。基于這個思路，1 024點定點FFT匯編實現就是將前四階合并運算寫入一次，第五、六階合并寫入一次，七、八階合并寫入一次，九、十階合并寫入一次，即前四階合并，其余兩階合并后將結果寫入內存。簡單說明前四階蝶形運算合并思路：

xr3=n||u2=u0+4||u4=u0+8||u6=u0+12

xr4=r3lshift -7

lc3=xr4

_cfft4:

讀||定義旋轉因子

讀||定義旋轉因子||計算

…

_cfftloop4:

讀||寫||計算

…

if lc3 b _cfftloop4

由于前四階每次計算128個定點數，所以N點FFT算法所需要前四階計算的循環次數是xr4=N/128。在_cfft4模塊中，首先讀取128個定點數,定義旋轉因子，并進行合并第一次四階蝶形運算。在_cfftloop4模塊中繼續讀取輸入，并行把在_cfft4模塊中合并第一次四階蝶形運算結果寫入到存儲器中，同時也并行讀取的下一組128個定點數的蝶形運算。if lc3 b _cfftloop4基于零開銷循環寄存器lc3的條件跳轉指令，只要lc3不等于0，零開銷循環寄存器lc3就自動減1，而且將跳轉到_cfftloop4模塊循環執行四階合并；若lc3等于0，說明N點的四階合并已經全部完成，就順序向下執行，不再執行跳轉。用零開銷循環來判斷N點的四階合并是否全部已經完成，可以大大減少代碼量，同時增加程序循環執行的效率。其余的兩階合并與前四階合并的思路是一致的，利用多階合并的方式比每一階都將中間結果寫入內存中節省了輸入輸出的訪存時間。

1.2.4 指令并行、軟件流水、循環展開

在FFT算法優化時，指令并行、軟件流水、循環展開這三種優化方法一般都是交叉使用的，在這里把兩階合并后的結果與旋轉因子合并運算的匯編程序來具體介紹這三種優化方法。

(1)指令并行

r5:4=[u0+=u10,u11]

r7:6=[u0+=u10,u11]r11:10=[w0+=w5,w6]

chr17=chr7*chr11

chr16=chr6*chr10

chr23=(chr5+chr17)/2

chr22=(chr4+chr16)/2

考慮到指令并行的原則，將程序優化為

r5:4=[u0+=u10,u11]||r11:10=[w0+=w5,w6]

r7:6=[u0+=u10,u11]

chr17=chr7*chr11||chr16=chr6*chr10

chr23=(chr5+chr17)/2||chr22=(chr4+chr16)/2

由此可見，原來占用7行指令行的程序現在值占用4行，一個蝶形運算就減少了3個實際運行周期。

(2)軟件流水、循環展開

由編排規則可知，計算結果和讀訪存指令結果需要隔兩行使用，等待寫入寄存器的數據需要提前兩行準備好，所以在這個規則下，僅僅進行指令并行遠遠不夠，會存在許多氣泡行使流水線出現卡拍問題。為了沖掉中間的氣泡行使得流水線盡量不出現停頓，減少實際運行周期，程序基于軟件流水、循環展開繼續優化。

r5:4=[u0+=u10,u11]||r11:10=[w0+=w5,w6]

r7:6=[u0+=u10,u11]

r13:12=[u0+=u10,u11]||r9:8=[w0+=w5,w6]||

chr17=chr7*chr11||chr16=chr6*chr10

r15:14=[u0+=u10,u11]||chr23=(chr5+chr17)/2||chr22=(chr4+chr16)/2

r35:34=[u0+=u10,u11]||r3:2=[w0+=w5,w6]||chr19=chr15*chr9||chr18=chr14*chr8

r37:36=[u0+=u10,u11]||chr25=(chr13+chr19)/2||chr24=(chr12+chr18)/2

r5:4=[u0+=u10,u11]||r11:10=[w0+=w5,w6]||chr21=chr37*chr3||chr20=chr36*chr2

r7:6=[u0+=u10,u11]||chr27=(chr37+chr21)/2||chr26=(chr36+chr20)/2

_cfft1loop：

[v0+=v10,v11]=r23:22||r13:12=[u0+=u10,u11]||r9:8=[w0+=w5,w6]||chr17=chr7*chr11||chr16=chr6*chr10

[v0+=v10,v11]=r25:24||r15:14=[u0+=u10,u11] ||chr23=(chr5+chr17)/2||chr22=(chr4+chr16)/2

[v0+=v10,v11]=r27:26||r35:34=[u0+=u10,u11]||r3:2=[w0+=w5,w6]||chr19=chr15*chr9||chr18=chr14*chr8

r37:36=[u0+=u10,u11]||chr25=(chr13+chr19)/2||chr24=(chr12+chr18)/2

chr21=chr37*chr3||chr20=chr36*chr2

chr27=(chr37+chr21)/2||chr26=(chr36+chr20)/2

.code_align 16

If lc0 b _cfft1loop||r5:4=[u0+=u10,u11]||11:10=[w0+=w5,w6]

優化后代碼的指令并行性大大提高，充分利用核內的4個執行宏，循環核心代碼并行執行寫入結果指令，讀取下一循環所用數據指令和點乘、疊加運算指令，充分利用了硬件資源，大大提高了程序運行效率。

2 實驗與分析

實驗平臺為BWDSP1042，Win10系統，Matlab版本為32位Matlab2012a，VS版本為VS2010，ECS版本為ECS 2.0。不同點數的輸入數據來自于Matlab程序產生的數據文件以及相應的旋轉因子文件。

2.1 實驗結果及分析

匯編程序優化之前編寫C語言程序，根據測試無誤的C語言程序框架進行FFT匯編。本文重點介紹FFT基于BWDSP1042底層優化，C語言相關操作不再贅述。在BWDSP1042配套的集成開發環境ECS 2.0中完成匯編程序，使用Matlab產生數據以及生成誤差圖。

使用Matlab程序來驗證FFT算法編寫的正確性。將Matlab程序產生的輸入數據和旋轉因子加載到ECS中運行FFT匯編程序，將FFT匯編輸出結果導出到一個指定的文本文件output.txt中，然后使用Matlab讀取txt文件中存放的匯編輸出數據，進行圖形可視化，如圖4所示。同時,Matlab調用自身FFT函數讀取同樣的輸入數據，將計算結果進行可視化，如圖5所示。

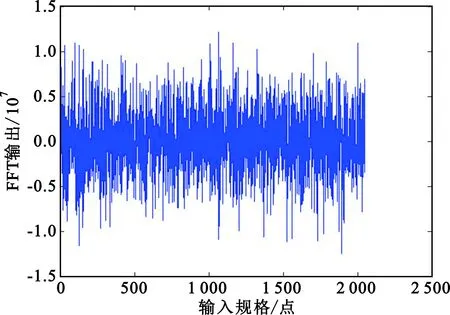
圖4 FFT匯編結果圖

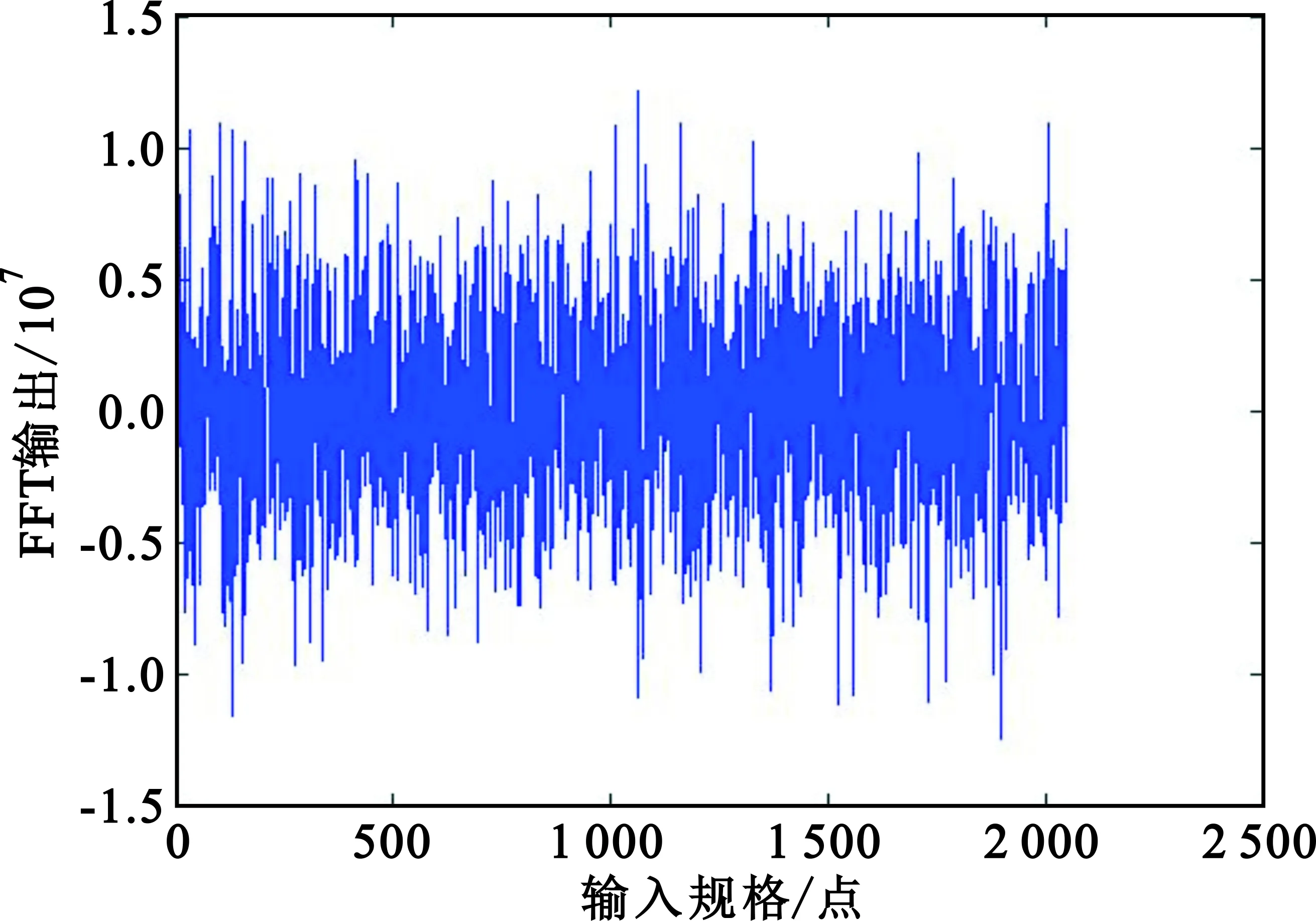
圖5 Matlab結果圖

由于Matlab中的函數庫都已被廣泛使用，其正確性毋庸置疑，所以將Matlab輸出結果作為匯編優化函數的基本參照標準，將本文研究的算法與Matlab中FFT函數的輸出結果進行對比，觀察圖4和圖5，結果幾乎一致，說明本文算法功能正確。為了進一步確定匯編算法的正確性，進行計算相對誤差，如圖6所示。

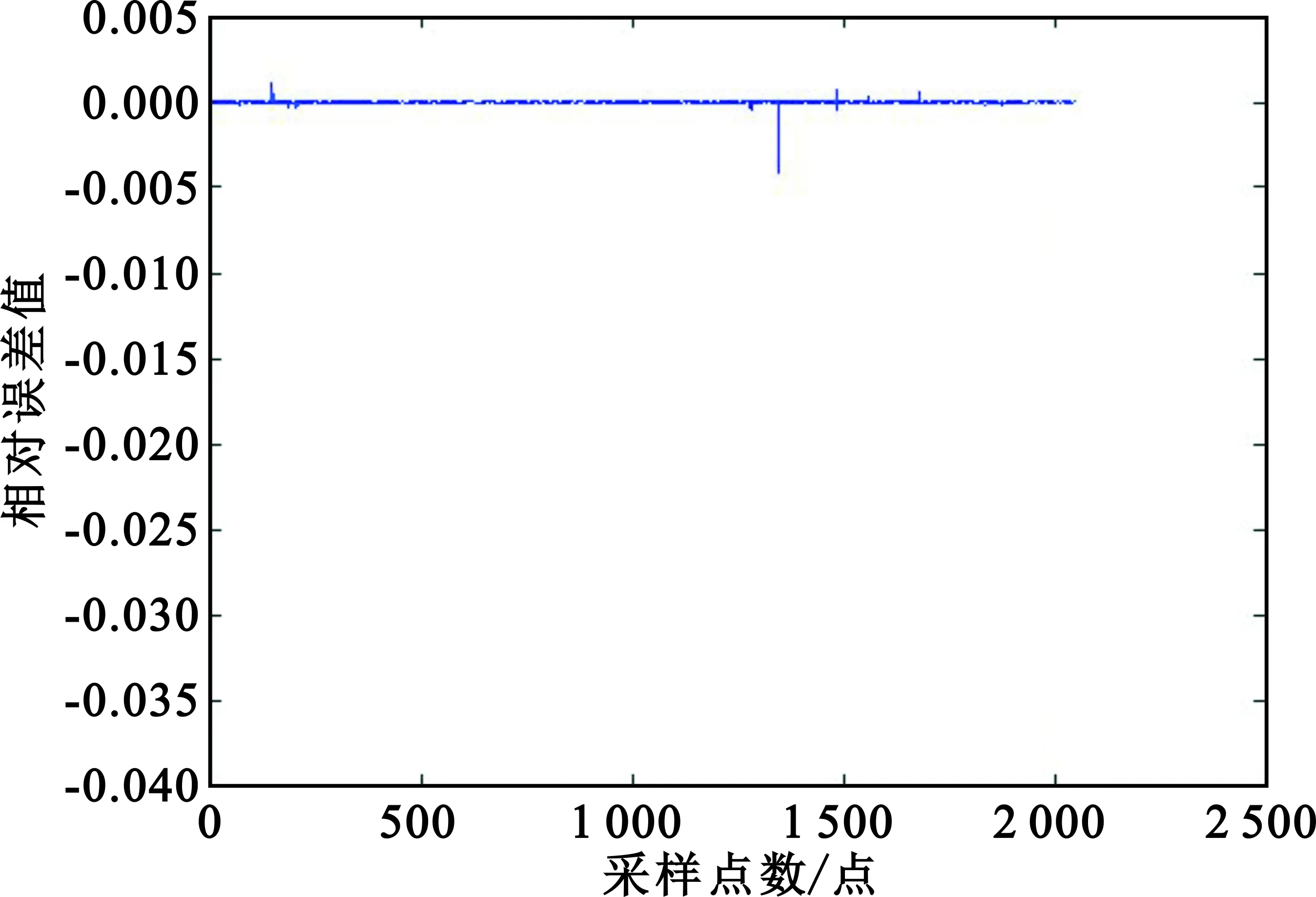
圖6 相對誤差圖

觀察圖6可知，FFT匯編程序的輸出結果與在Matlab中運行FFT函數的誤差，大部分輸入的計算結果基本一致，誤差在0附近，在1 350點左右出現-0.004左右偏差。由于輸入數據都是Matlab隨機生成的浮點數，需要通過格式轉換為定點數，實現定點數FFT匯編，在數據轉換時也會出現些許誤差，對輸出誤差也有相應影響。由圖可知，輸出誤差在10-3級別，也在函數開發誤差要求范圍之內，說明基于BWDSP1042的FFT算法匯編正確。測試基于不同點數的FFT實際運行周期，并與BWDSP100、TMS320C6678函數對比，結果如表1所示。

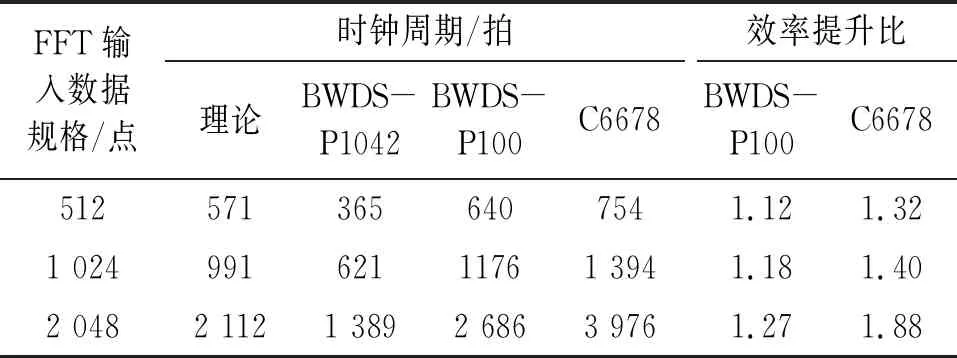
表1 BWDSP1042實際周期比較

由周期指標可知，基于BWDSP1042的FFT算法實際運行周期應小于理論時鐘周期的1.5倍。由表1可知，512點、1 024點、2 048點的FFT的實際運行周期分別為571拍、991拍、2 112拍，經計算該算法不同輸入點數均滿足函數庫開發要求。本文將基于BWDSP1042的FFT算法與BWDSP100和TMS320C6678這兩款高性能芯片應用函數庫中的FFT算法的實際運行周期進行比較，運算效率均提升一倍以上，說明本文所研究的FFT算法在BWDSP1042的性能優化同時也體現了算法的實用性和優越性。

2.2 硬件資源成本

本文實現的N點的32位定點復數FFT共有lb(N)階，每階有N/2個蝶形運算，每個蝶形運算需要完成一次復數乘法、兩次復數加法，所以完成一個蝶形運算需要4個加法器和4個乘法器。FFT函數主要是蝶形運算，從蝶形運算角度說明硬件資源消耗情況，如表2所示。

表2 硬件資源消耗說明

BWDSP1042中有4個增強的運算宏eC104+，每個宏中內部有8個加法器和8個乘法器，所以N/2個蝶形運算需要利用這些乘法器和加法器完成計算，大點數FFT運算對資源消耗的硬件成本更多。另外，FFT算法在實時性方面有一定要求，進而對BWDSP1042硬件性能具有較高要求，增加了硬件成本。

3 結束語

本文基于BWDSP1042的體系架構以及指令特點，改進了基-2時間抽取FFT算法結構，減少了FFT算法運算時間，優化了性能。定點格式的FFT算法由于進行了數據縮放，導致精度降低，雖然并不影響正確性，但應用于要求高精度的領域仍需繼續提升精度指標。本文研究不僅對數字信號處理相關應用領域時頻轉換時間有一定的改善，而且對國產化芯片BWDSP1042的商業化應用以及走向工程應用具有實際意義。高性能FFT運算是芯片走向實際應用的重要一環，接下來的工作是在本研究基礎之上，開發國產多核處理器BWDSP1042具有通用標準參數的高效率底層其他優化算法函數庫，實現函數庫與軟件開發環境的集成，滿足大多數用戶使用，為DSP核心器件國產化打下基礎，為該芯片成功推向民用市場奠定基礎。