多卷積神經網絡融合的滾動軸承故障識別方法

□ 郭雙全

上海電氣集團股份有限公司 中央研究院 上海 200070

1 研究背景

滾動軸承是風電機組、汽輪機、電動機、機床等工業旋轉類設備的重要零部件。滾動軸承故障,易造成較大的停機損失和影響。因此,及時識別或預警滾動軸承的故障狀態,對于保障設備安全運行和高效運維有重要意義。

在工程實踐中,為保障大型設備可靠運行,往往配備在線監測系統,對振動、電氣、壓力等關鍵參數進行動態高頻采樣監測。采用傳統故障狀態診斷方法時,通過時域分析、頻域分析、時頻分析等進行特征提取[1-3],通過支持向量機、神經網絡、隨機森林等方法進行故障狀態識別[4]。隨著深度學習技術在視覺和語音識別方面的快速發展,部分學者開始研究卷積神經網絡在軸承故障診斷方面的應用[5]。李恒等[6]提出短時傅里葉變換和卷積神經網絡相結合的軸承故障診斷方法。韓樹發等[7]提出一種改進的深度遷移學習算法——聯合領域自適應算法,與卷積神經網絡相結合,進行多工況故障診斷,效果優于單一卷積神經網絡。

雖然采用卷積神經網絡可以在一定程度上實現對軸承故障狀態下復雜時頻特征的提取,但是模型層數和模型參數的確定需要多次嘗試和較多的經驗,還未形成可靠的方法,往往訓練的模型泛化性能不足。集成學習算法可以通過對多個弱學習器的融合,顯著提高模型的泛化性能[8]。由此,筆者針對振動信號時頻譜圖,即短時傅里葉變換譜的數據結構特點,設計三個不同的卷積神經網絡模型,通過全連接神經網絡對這三個不同的卷積神經網絡進行融合,采用常用的引導聚集集成學習方法訓練融合模型,實現對滾動軸承故障狀態的智能識別。通過試驗將融合模型與單一卷積神經網絡模型對比,從模型測試結果準確性、訓練過程穩定性及效率等方面進行對比分析。

2 多卷積神經網絡融合設計

滾動軸承的振動信號是典型的非平穩信號,一般采用時頻分析作為振動信號處理的基本方法。常見的時頻分析方法包括短時傅里葉變換、小波變換、S變換、希爾伯特-黃變換等。時頻分析得到的時頻譜圖反映出滾動軸承振動信號在不同時間與頻率維度下的能量強度,可以多角度展現振動信號的細節變化,有效描述振動信號細微變化的滾動軸承故障特征。

2.1 預處理

筆者采用短時傅里葉變換方法對滾動軸承振動信號進行預處理,得到時頻譜圖。短時傅里葉變換方法采用固定長度的窗函數對振動信號進行截取,對截取的振動信號進行傅里葉變換計算,得到某時刻的局部頻譜。連續在時間軸上移動窗函數,截取振動信號進行傅里葉變換,最終得到不同時刻的局部頻譜的集合,結果為關于時刻t與頻率f的二維函數。短時傅里葉變換方法理論公式為:

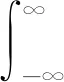
(1)

式中:τ為時刻;x(τ)為時刻τ的振動信號;ω(τ-t)為時刻τ與時刻t時間差對應的窗函數。

在實際信號處理中,振動信號一般為離散的高頻采樣序列,需要采用短時傅里葉變換離散計算公式:

(2)

式中:m為離散采樣時刻順序;n為離散頻率點順序;s[k]為第k個離散采樣時刻信號;γ(k-m)為離散采樣時刻順序k與m差值對應的離散窗函數;L為離散窗函數長度。

輸出的離散結果S[m,n]為二維時頻譜圖,如圖1所示。假設短時傅里葉變換輸出矩陣大小為Ms×Ns,時間維度Ms為56,頻率維度Ns為501。時頻譜圖反映了信號在不同時刻和頻率的幅值大小,既是時域和頻域特性的綜合體現,也可以看作是信號在Ms個不同時刻對應的頻率分布情況或信號在Ns個不同頻率對應的時間變化趨勢。

圖1 二維時頻譜圖

2.2 卷積神經網絡

卷積神經網絡一般由輸入層、卷積層、池化層、過渡層、全連接層、輸出層組成,通過多層特征提取層能自適應從輸入信息中充分挖掘抽象特征,具有較強的泛化能力和判別能力,同時具有對移動、縮放、扭曲不變性的特點。卷積神經網絡可以將振動信號預處理得到的時頻譜圖作為輸入層,進行自動特征提取識別時頻特性,實現狀態識別。

卷積層主要通過將輸入特征圖與多個卷積核進行卷積計算,加上偏置項,經過激活函數,輸出新的特征圖。假設卷積層的輸入特征圖包含N個通道,輸出特征圖包含M個通道,則有[9]:

(3)

式中:Cq為卷積層輸出特征圖第q個通道矩陣;Xp為輸入特征圖第p個通道矩陣;Wpq為輸入特征圖第p個通道矩陣在進行卷積計算得到輸出特征圖第q個通道矩陣時采用的卷積核權重矩陣;bq為偏置項;F為激活函數。

池化層主要對輸入特征圖進行計算變換,包括最大值池化、平均值池化、隨機值池化等,輸出尺寸較小的特征圖,同時保持特征基本尺度不變。池化層一般只改變特征圖的尺寸大小,不做權值更新。

過渡層一般作為卷積層或池化層與全連接層連接的過渡層,將輸入特征圖展開為一維特征向量,不做實際計算。

全連接層對輸入的一維特征向量進行加權求和偏置,通過激活函數,輸出新的一維特征向量,計算式為:

(4)

式中:yv為全連接層輸出特征向量對應值;xu為全連接層輸入特征向量對應值;U為全連接層輸入特征向量總數;J為全連接層輸出特征向量總數;wuv為對應權重因數;bv為偏置項;θ為激活函數。

為設計出合適的卷積神經網絡結構,需綜合考慮輸入圖像大小、各層類型、卷積核大小與數量等多種因素。一般采用常用的深度學習網絡,結合數據特點和專業經驗進行修改,通過改變各層網絡參數或適當增加網絡層數,建立適合根據滾動軸承短時傅里葉變換時頻譜圖進行故障診斷的網絡模型。

LeNet-5是一種用于手寫體字符識別的非常高效的卷積神經網絡[10]。這一卷積神經網絡總共包括七層:三層卷積層、兩層池化層、兩層全連接層,網絡將3像素×32像素×32像素手寫體圖片輸入數據轉換為10節點輸出向量,0～9代表模型識別的數字。筆者在LeNet-5網絡的基礎上,將短時傅里葉變換輸出矩陣呈現的時頻譜圖作為輸入,根據時頻譜圖在時域和頻域不同的尺度大小,以及不同的卷積操作形式,改變網絡參數,設計典型的卷積神經網絡模型,將時頻譜圖輸入數據轉換為對應的滾動軸承故障狀態的節點輸出。

為了充分應用卷積神經網絡綜合提取滾動軸承振動信號預處理得到的時頻譜圖特征,筆者考慮設計三個不同的卷積神經網絡:二維卷積神經網絡、一維時域卷積神經網絡、一維頻域卷積神經網絡。

將短時傅里葉變換Ms×Ns輸出矩陣呈現的時頻譜圖作為單通道二維圖像,構建二維卷積神經網絡,對應二維的卷積核和池化核。二維卷積神經網絡能夠利用卷積特性在頻域和時域上同時提取特征。二維卷積神經網絡如圖2所示,包括輸入層、三個卷積層、三個池化層、過渡層、三個全連接層、輸出層。其中,輸入層為時頻譜圖的簡化表示,各個卷積層和池化層的輸出為對應的特征圖,過渡層用于將池化層的輸出特征圖平鋪展開為一維特征向量,與全連接層的神經元一一映射。圖2中各標識數字為網絡設計參數,如“輸入層1通道501×56”表示輸入層為單通道,Ns為501,Ms為56;“卷積層15×3核”表示卷積層采用對應大小的二維卷積核;“特征圖3通道164×54”表示經過卷積層計算后輸出的特征圖包括三個通道,每個通道的大小為164×54;“隱含神經元400個”表示與全連接層相連的隱含神經元的數量。輸出層的節點數對應軸承故障的狀態數。

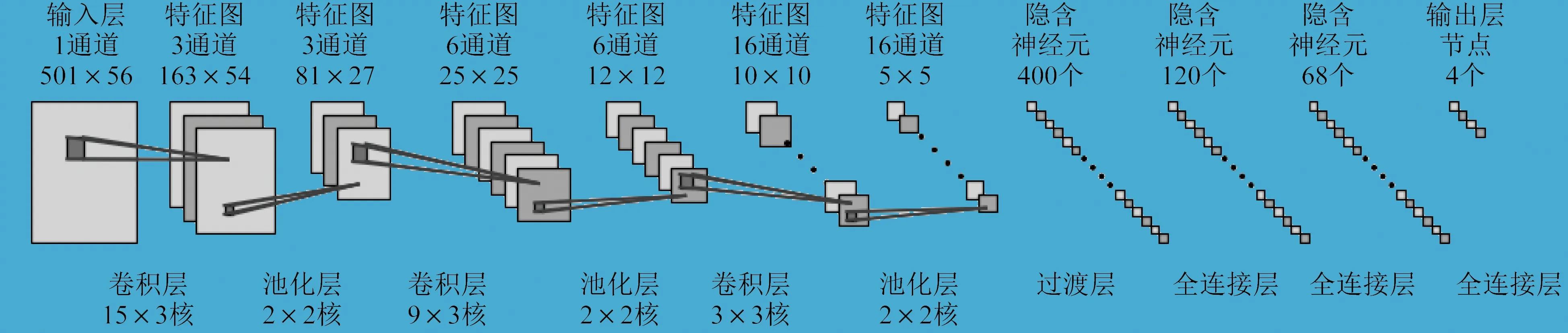
圖2 二維卷積神經網絡

可以將短時傅里葉變換輸出矩陣呈現的時頻譜圖看作按頻率維度劃分的對應Ns個頻率通道的時間變化子圖的集合,從而構建一維時域卷積神經網絡,對應一維的卷積核和池化核。一維時域卷積神經網絡側重利用卷積特性在時域上提取特征。一維時域卷積神經網絡如圖3所示,包括輸入層、三個卷積層、兩個池化層、過渡層、三個全連接層、輸出層。其中,輸入層是時頻譜圖按頻率維度進行通道劃分后的簡化表示,各個卷積層和池化層的輸出為對應的特征圖。

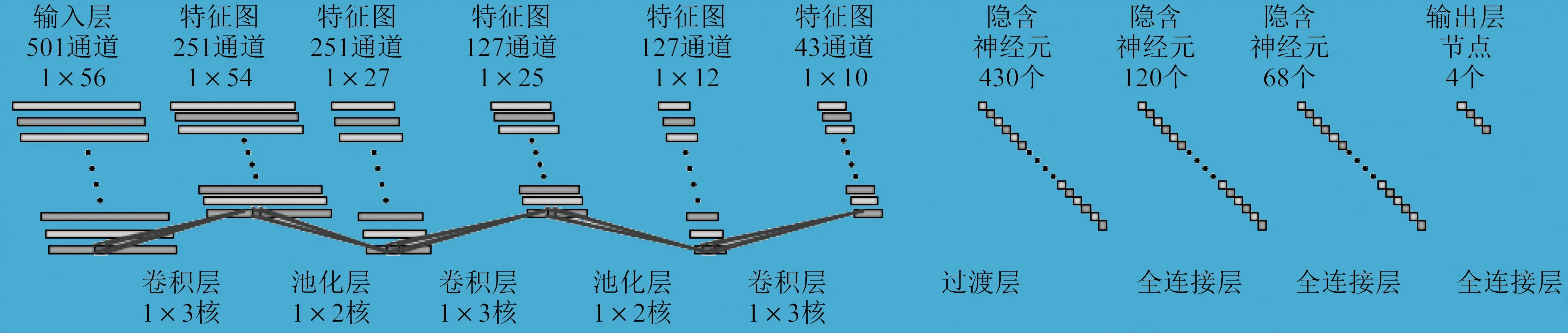
圖3 一維時域卷積神經網絡

可以將短時傅里葉變換輸出矩陣呈現的時頻譜圖看作按時間維度劃分的對應Ms個時間通道的一維頻率分布子圖的集合,從而構建一維頻域卷積神經網絡,對應一維的卷積核和池化核。一維頻域卷積神經網絡側重利用卷積特性在頻域上提取特征。一維頻域卷積神經網絡如圖4所示,包括輸入層、三個卷積層、兩個池化層、過渡層、三個全連接層、輸出層。其中,輸入層是時頻譜圖按時間維度進行通道劃分后的簡化表示,各個卷積層和池化層的輸出為對應的特征圖。

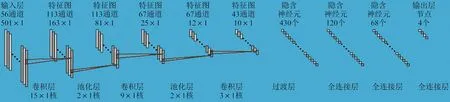
圖4 一維頻域卷積神經網絡

3 集成學習

集成學習時,訓練若干個個體學習器,通過一定的結合策略,形成一個強學習器。根據個體學習器之間依賴關系的不同,集成方法一般分為引導聚集算法和提升算法兩種。筆者采用引導聚集算法對設計的三個不同卷積神經網絡進行集成,形成融合模型。集成學習如圖5所示。

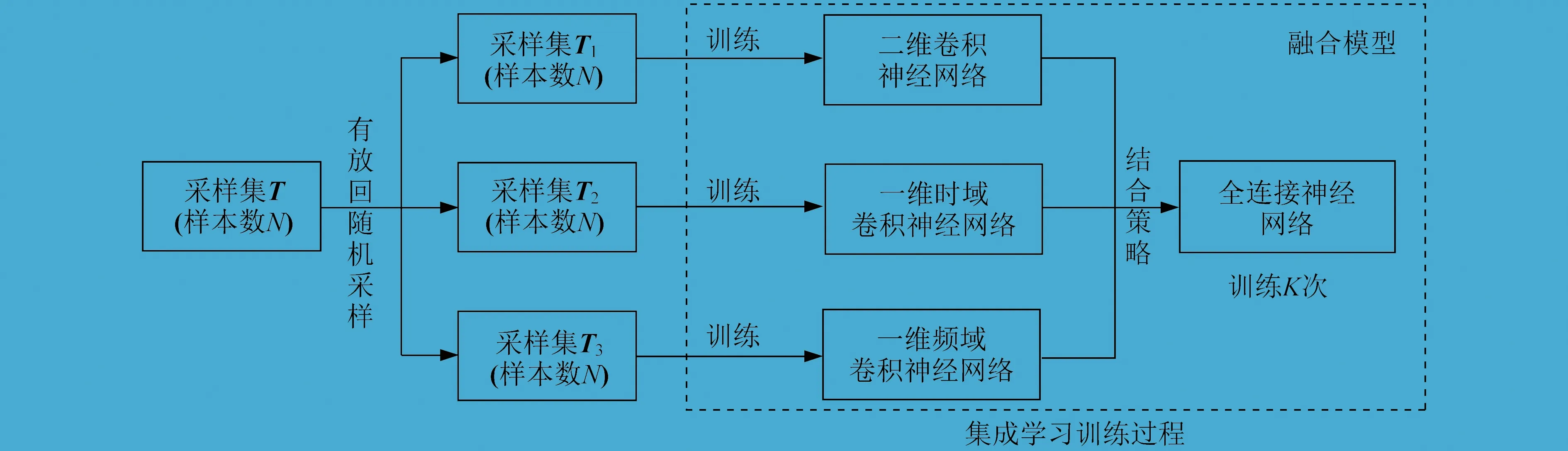
圖5 集成學習

引導聚集算法首先通過對樣本數為N的訓練集T進行有放回的隨機采樣,構建出與訓練集大小相同的采樣集T1、T2、T3,然后利用采樣集分別訓練二維卷積神經網絡模型、一維時域卷積神經網絡模型、一維頻域卷積神經網絡模型,最后對這三個卷積網絡模型的輸出采用結合策略集成,一般結合策略包括平均法、投票法、學習法。筆者采用學習法設計一種常規全連接神經網絡進行集成,最終得到融合模型。全連接神經網絡的輸出即為融合模型的最終輸出結果。全連接神經網絡如圖6所示,包括輸入層、隱含層、輸出層。將前述三個不同卷積神經網絡模型的輸出結果作為輸入層,經過隱含層計算后輸出最終結果,即為軸承的故障狀態。

圖6 全連接神經網絡

4 試驗分析

為驗證模型訓練效果,采用滾動軸承振動數據集,經過處理得到某滾動軸承在正常、外圈故障、內圈故障、滾動體故障時,受到不同轉速和負載情況的振動信號樣本472條,每條樣本信號的采樣頻率為12 000 Hz,采樣時長為1 s。滾動軸承正常、外圈故障、內圈故障、滾動體故障四種狀態的樣本數依次為a、b、c、d。

采用前述步驟,將樣本劃分為訓練集和測試集,進行對比訓練,比較融合模型和單一卷積神經網絡模型在訓練精度和效率上的差異。訓練策略為通過集成學習對融合模型進行訓練,包括對二維卷積神經網絡模型、一維時域卷積神經網絡模型、一維頻域卷積神經網絡模型進行訓練,以及對全連接神經網絡訓練K次。將K設為10、30、50,逐漸增加集成學習的訓練次數,并在每次集成學習訓練后利用測試集對融合模型和單一卷積神經網絡模型進行驗證。驗證準確率隨集成學習訓練次數的變化曲線如圖7所示。

以驗證準確率99%為基準,由圖7可以看出,融合模型比三個單一卷積神經網絡模型更快收斂達到基準,并且訓練過程更為穩定,而單一卷積神經網絡訓練過程中存在一定的震蕩。另一方面,不同K值對應的融合模型收斂次數并無明顯變化,表明采用全連接神經網絡進行融合具有較好的泛化能力,在實際應用中選取較小的K即可達到提高準確率的效果。

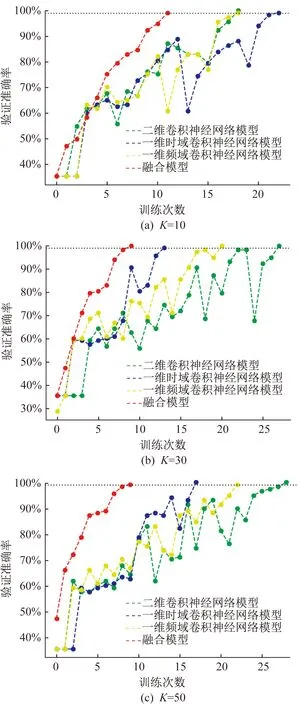
圖7 驗證準確率隨集成學習訓練次數變化曲線

為進一步驗證融合模型對驗證準確率的改善效果,對固定K值的三種情況分別進行三次重復試驗,共計九次,統計各次試驗中融合模型和各單一卷積神經網絡模型分別達到驗證準確率99%所需的訓練次數,具體見表1。由表1數據可以看出,融合模型所需訓練次數相比單一卷積神經網絡模型所需訓練次數明顯減少,具有較好的穩定性。

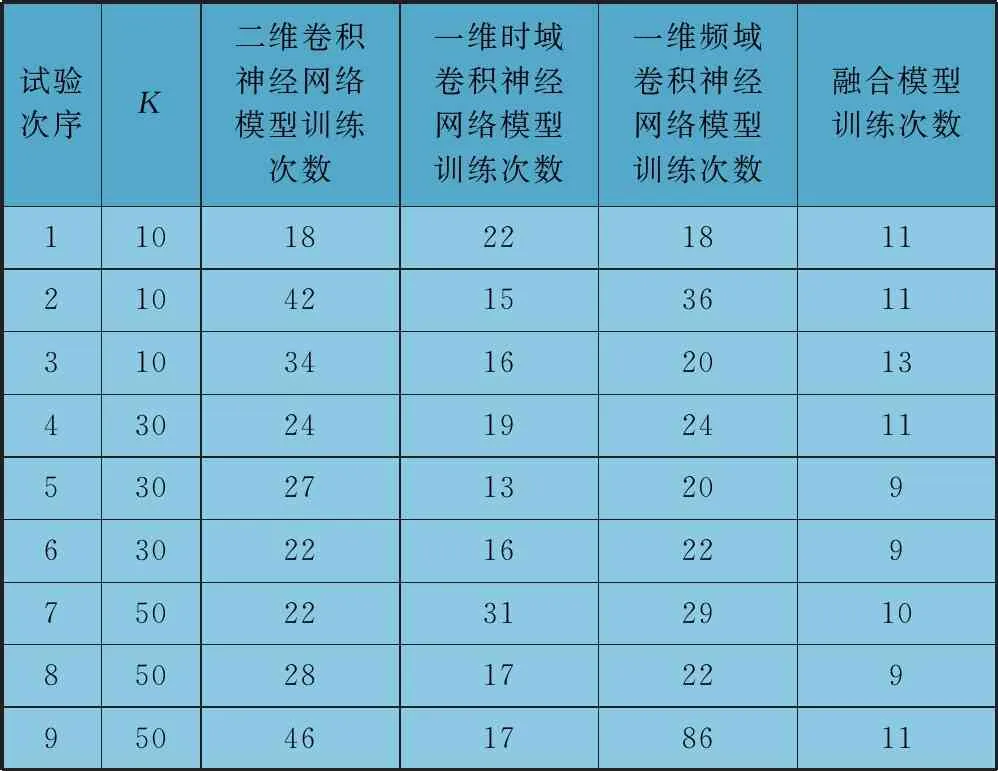
表1 驗證準確率達到99%試驗結果

5 結束語

筆者提出的多卷積神經網絡融合的滾動軸承故障識別方法,集成了多種不同結構類型的卷積神經網絡,提高了對滾動軸承振動信號時頻特征的提取能力。試驗結果表明,與單一卷積神經網絡模型相比,通過集成學習得到的多卷積神經網絡融合模型能夠通過較少的訓練次數達到相同的驗證準確率,有效識別滾動軸承故障狀態,并且訓練過程穩定性和泛化性較好。后續可以通過優化網絡結構參數和改進集成學習策略,不斷提高模型對滾動軸承故障的識別精度。