光纖陀螺慣性平臺的穩定回路控制

徐白描，魏宗康，彭 迪

（北京航天控制儀器研究所,北京100039）

0 引言

陀螺慣性穩定平臺系統是以陀螺作為敏感元件,通過穩定回路實時測量和調整平臺臺體的姿態從而隔離載體角運動,以便為加速度計提供一個良好的工作環境,高精度慣性穩定平臺系統對于提高軍事化武器在目標打擊過程中的命中率與命中精度至關重要[1-2]。

液浮陀螺、撓性陀螺目前已具備了較成熟的技術,現有的慣性穩定平臺系統多采用氣浮陀螺、液浮陀螺或撓性陀螺作為敏感元件,但由于工藝、成本以及對軍事化打擊更高的精度要求等因素正逐漸被新型陀螺所取代。光纖陀螺是全固態光學陀螺,具有結構簡單、精度覆蓋面廣、可靠性高以及使用壽命長的優勢。因此,國外的光纖陀螺穩定平臺已經成功應用于武器系統中,我國對于光纖陀螺慣性穩定平臺的研究也日益重視。目前,國內多個科研院所都已開展了光纖陀螺穩定平臺的研發,其中對基于光纖陀螺的平臺穩定回路成為了研究重點。2007年,第二炮兵工程學院的周小剛等[3]提出了光纖陀螺慣性平臺穩定系統的設計方案。2016年,中國北方車輛研究所的劉義等[4]采用光纖陀螺替代撓性陀螺建立了慣性平臺穩定回路模型,并采用經典PID控制算法仿真驗證了光纖陀螺的可行性。這兩篇文章都沒有對控制器設計過程進行詳細的介紹,僅給出了設計結果。2015年,天津航海儀器研究所的毋興濤等[5]對由光纖陀螺構成的慣性穩定回路進行了關鍵技術分析,設計了串聯超前-滯后校正網絡,控制器的設計方法主要是根據經驗調節PID參數,運算量較大,并且對平臺穩定回路設計指標中的動態指標考慮不全面。以上研究對于光纖陀螺穩定回路設計具有借鑒意義,但也存在一定的局限性,比如沒有考慮光纖陀螺的滯后環節對穩定回路的相位影響,設計方法嚴重依賴于人的經驗知識等。

因此,本文提出了基于H∞控制理論的控制器設計方法,該方法可在性能指標的限制條件下基于計算機軟件程序快速解出控制器。基于該控制器,本文給出了基于光纖陀螺的平臺穩定回路仿真結果以及實際試驗對所設計控制器的驗證。

1 光纖陀螺慣性平臺穩定回路建模

以單條回路為例,構成穩定回路的主要部分為敏感元件、控制器、執行機構和穩定對象等。當有干擾力矩Mf作用在框架軸上時,臺體相對慣性空間發生轉動。相應地,光纖陀螺就會敏感到該轉動角速度,并輸出對應的信號經功率放大器輸出后驅動直流力矩電機,產生電機力矩抵消框架軸上的干擾力矩Mf,使平臺穩定在慣性空間。根據這個過程,給出的平臺系統穩定回路框圖如圖1所示[6-7]。

圖1 光纖陀螺穩定回路框圖Fig.1 Block diagram of fiber optic gyroscope stable loop

光纖陀螺的傳遞函數為

式（1）中,KD為直流增益,Bw為頻帶寬度,Td為延遲時間。

光纖陀螺傳遞函數的形式可描述為一階慣性環節、延遲環節、比例環節的串聯,三個環節對穩定回路系統開環傳遞函數頻率特性的影響如圖2所示。

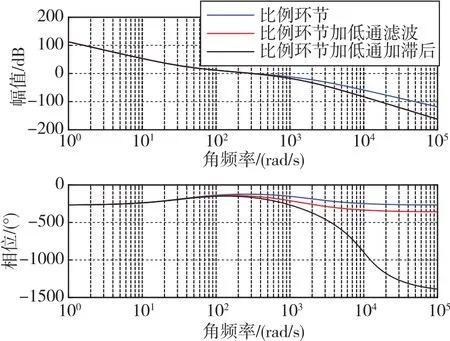
圖2 各環節對幅頻特性的影響Fig.2 Effects of various links on amplitude-frequency characteristics

如圖2所示,延遲環節不改變幅值特性,紅線與黑線重合,只在相頻特性中有明顯的相位延遲現象。為分析方便,控制器設計時暫不考慮延遲環節。根據圖1中伺服回路系統計算得到的開環傳遞函數為

將各項參數帶入未加以校正的系統,得到的開環Bode圖如圖3所示。

圖3 未校正系統的開環Bode圖Fig.3 Open loop Bode diagram of uncorrected system

如圖3所示,未加入校正裝置前,開環系統的截止頻率ωc＝1.94rad/s,相位裕度γ＝－0.0794°,幅值裕度為負無窮大,以上三項頻域指標均不滿足要求。為了得到穩定、角度無靜差的系統,需要設計校正環節對系統進行校正。

2 H∞控制器設計

本次控制器設計的性能指標要求為:2000g·cm常值干擾力矩作用下,平臺的角度靜差≤10″；在幅值為600g·cm、頻率為1Hz的正弦干擾力矩作用下,角度小于30″；回路調節時間小于0.1s；幅值裕度大于8dB,相角裕度大于25°。平臺穩定回路的框圖如圖4所示。

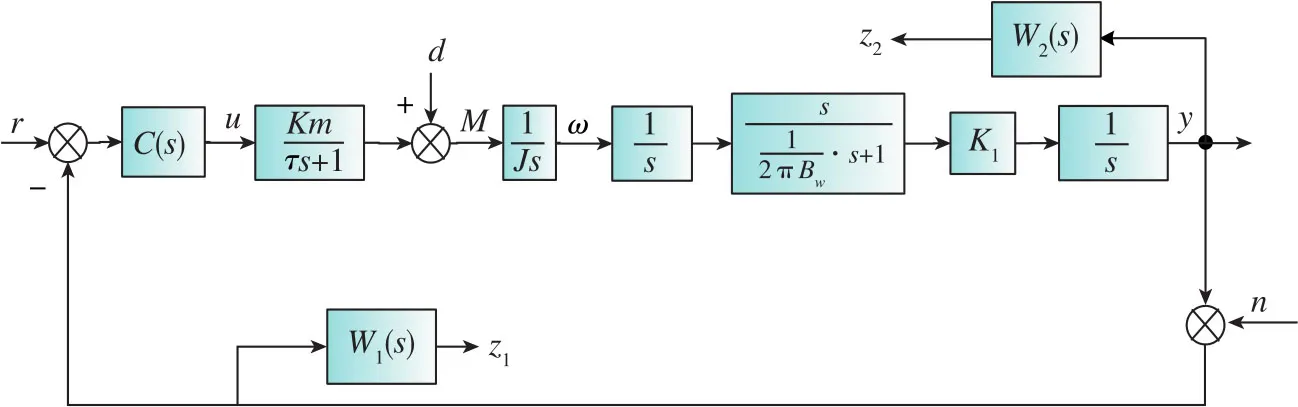
圖4 約束條件下的光纖陀螺穩定回路框圖Fig.4 Block diagram of fiber optic gyroscope stable loop under constraint conditions

圖4中,W1（s）和W2（s）分別為性能界函數和對象不確定性界函數；u為控制的輸入信號,是被控對象的輸入信號；y為反饋量,是被控對象的輸出量；r為校正環節輸入端信號,n為干擾信號,z為評價信號。 設控制器C（s）＝KWc（s）, 被控制對象可求得

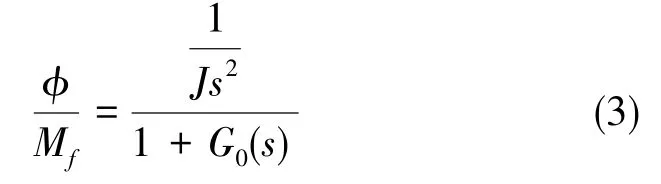
式（3）中,G0（s）為系統開環傳遞函數。

在幅值為6°、頻率為1Hz下的要求為

考慮系統的輸入和輸出關系以及誤差信號,有

式（5）中,S（jω）為系統的靈敏度函數。 靈敏度函數是決定跟蹤誤差大小最重要的指標,當靈敏度函數的奇異值越低,則系統的跟蹤誤差越小,也即對干擾的抑制能力越強。令它可同時滿足動靜態指標[10-11],則靈敏度函數為

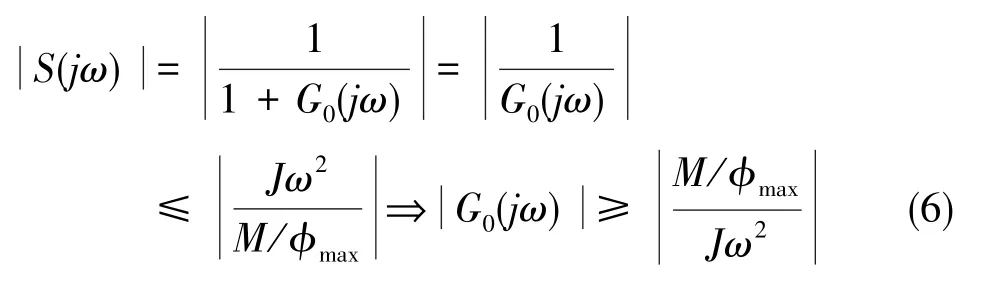
那么,它的性能指標為

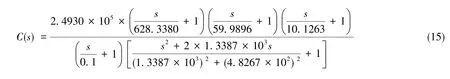
校正后的系統開環傳遞函數Bode圖如圖5所示,滯后環節不影響幅值特性,但會影響相位。由圖5（a）可知, 剪切頻率為ωc＝163.07rad/s。 由圖5（b）可知,未考慮滯后環節時,系統的相角裕度為53.96°,幅值裕度為22dB；考慮滯后環節時,系統相角裕度為44°,幅值裕度為14.9dB。可以得出,所設計的控制器仍然滿足精度和魯棒穩定性。

圖5 系統開環傳遞函數Bode圖Fig.5 Bode diagram of system open loop transfer function

3 試驗結果及分析

3.1 仿真驗證

1）單位階躍仿真驗證

為驗證控制器的性能,對平臺穩定回路進行單位階躍響應仿真,結果如圖6所示。

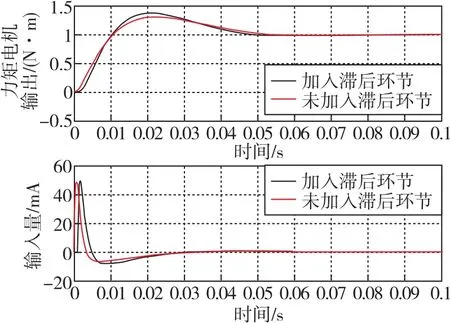
圖6 穩定回路單位階躍響應Fig.6 Diagram of stable loop step response

由圖6可知,加入滯后環節后,系統響應存在1ms的時間延遲,超調量有所增加。

2）正弦仿真驗證

為驗證穩定回路在動態條件下的性能,對框架加入幅值為600g·cm、頻率為1Hz的正弦干擾力矩進行仿真,如圖7所示。由圖7可知,框架軸轉動角度為1.07″,小于30″,穩定回路的設計滿足動態性能指標要求。

圖7 正弦干擾力矩下框架角的輸出Fig.7 Output of frame angle under sinusoidal interference torque

3.2 閉合試驗

對光纖陀螺穩定平臺進行單通道閉環試驗。圖8為光纖陀螺采集到的閉合前后的數據,采樣時間為5ms,采集時長2min。可以看出,在平臺上電10s后對平臺進行閉合,穩定回路快速回到零位,此時陀螺輸出均值為零。

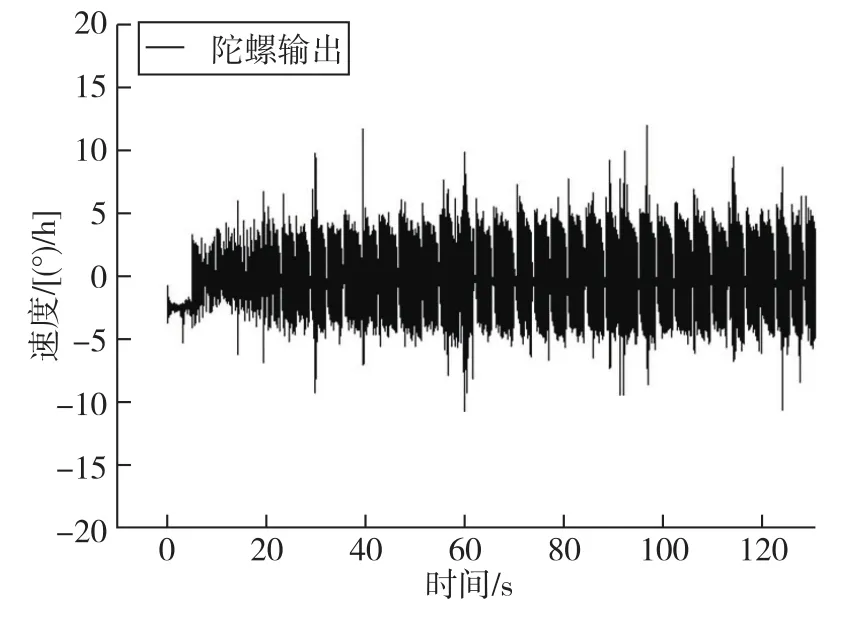
圖8 光纖陀螺的輸出信號Fig.8 Output of fiber optic gyroscope

雖然平臺穩定回路閉合正常,但可以看出光纖陀螺的輸出噪聲較大,瞬時幅值可達10（°）/h。為分析噪聲原因,利用Allan方差對陀螺閉合后的輸出信號進行分析。圖9為噪聲信號的功率譜密度曲線,圖10為對噪聲信號計算Allan方差得到的標準差-相關時間雙對數曲線。

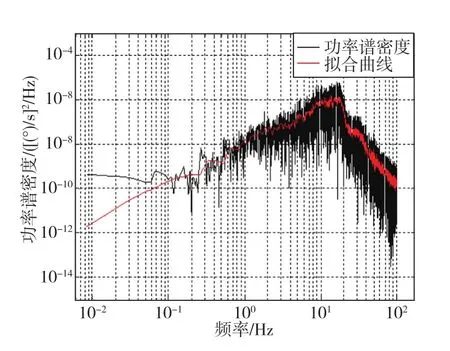
圖9 功率譜密度分析Fig.9 Diagram of power spectral density analysis

圖10 光纖陀螺的Allan方差圖Fig.10 Allan variance diagram of fiber optic gyroscope

由圖9可知,陀螺噪聲信號在16Hz左右幅值最大,隨后出現衰減,與系統所設計的轉折點位置相符。圖10中的Allan方差分析結果表明,對于該光纖陀螺,其量化噪聲為主要噪聲源,由于采樣時間太短,計算結果中沒有反映出零偏不穩定性的估計結果。 在相關時間為 5×10－3s～2×10－2s內,曲線有一段斜率為零的線段,這并不是零偏不穩定性的估計結果。

4 結論

本文重點分析和研究了以光纖陀螺作為傳感器的慣性平臺穩定回路控制技術。根據動靜態指標及裕度指標,基于H∞控制理論對某型號光纖陀螺慣性平臺進行穩定回路設計,通過仿真驗證了穩定回路的性能。同時,為了驗證滯后環節對穩定回路性能的影響,在仿真時考慮了光纖陀螺的滯后環節。結果證明,加入滯后環節會造成相位延遲,但是所設計的穩定回路仍然可以滿足性能指標,說明控制器具有較好的魯棒性。最后進行了穩定回路閉合試驗,利用Allan方差法對穩定回路閉合后的光纖陀螺輸出噪聲進行了分析,分離出光纖陀螺信號中的主要隨機誤差,驗證了控制器的正確性。